基于改进logistic模型法的配电网负荷预测

余泳涛，张扬

(1.南昌大学信息工程学院，江西 南昌 330031；2.国网江西省信息通信分公司，江西 南昌 330031)

为了实现“碳达峰”“碳中和”的“双碳”目标，加快构建以新能源为主体的新型电力系统，需要打造一个“安全可靠、经济高效、运行灵活、主配协调”的配电网[1]。电网规划的基础是配电网负荷预测，负荷预测直接影响着地区配电网络的建设。在传统预测中，往往将规划区域看作是一个整体，求取其总负荷，传统负荷预测主要采用回归分析法、增长曲线法和时间序列法[2-4]等方法。而现代负荷预测方法有模糊预测法、灰色预测法、神经网络法[5-7]等等。准确的配电网负荷预测对于城市配电网规划有着至关重要的作用，其中远景负荷预测可以为地区目标网架搭架提供支撑，近期负荷预测可以对站点布置、建设时序、电力平衡等环节提供帮助[8-9]。可见，研究配电网负荷预测既具有理论意义，又具有现实指导意义[10]。

常规配电网规划的负荷预测中，通常以自然增长法和点负荷法[11]作为求取过渡年负荷增长速度的方法，人为给定一个增长率，不符合地区发展规律，且过渡年和饱和年的界定不够平滑，因此，如何求取过渡年的负荷发展规律，成为亟待解决的问题。

1 饱和年负荷预测

在城市配电网规划过程中，对于地区用电负荷的求取，往往采用空间负荷预测法，其在时间上可以预测地区负荷饱和时的状态，在空间上可以预测负荷的分布信息，为配电网规划提供科学依据[12]。城市饱和负荷是对该城市未来负荷发展状况的一种合理估计，通过对城市发展水平、资源条件、经济结构、科技能力以及政策措施等进行综合评估，并结合本地区发展情况以及发展成熟地区同等类型城市负荷情况，以城市发展规划为依托，采用以空间负荷预测为代表的先进的、科学的预测方法得到[13-14]。

负荷密度法是进行空间负荷预测的一种比较成熟的方法，即类比已达到规划目标年预期用电水平的典型地块及用户的用电情况为样本，计算典型负荷密度指标，开展逐个地块或用户的负荷预测，并汇总得到整个规划区的总负荷[15-22]。其预测公式为

P0=(∑DSη)φ

(1)

式中：P0为最大负荷，MW；D为负荷密度指标，MW·km-2；S为用地面积，km2；η为容积率；φ为同时率，由历史负荷情况推算得到。

2 过渡年负荷预测

新开发建设地区的负荷发展过程，一般分为初期发展阶段、中期发展阶段、后期发展阶段和饱和发展阶段4个阶段，logistic模型可以较为准确地描绘这一规律。

2.1 改进logistic模型法

传统的logistic曲线模型拟合效果差，不考虑一些随机因素的影响，预测值往往会与真实值差距较大，难以满足预测要求，文献[23]在此基础上提出了一种改进logistic数学模型，引入随机变量C，该变量根据已知数据的拟合自动调整，对于曲线收敛效果和历史数据拟合精度有一定的提升。其改进之后的模型为

(2)

式中：Pt为地区负荷值；a,b,k,C均为模型参数，且k>0,a>0,b>0。

但是式(2)无法反映该地区饱和预测的情况，缺少对未来影响该地区负荷增长因素的考虑，因此将饱和值引入该模型，改进的结果为

(3)

式中：P0为饱和负荷数据。

求式(3)的一阶导数为

二阶导数为

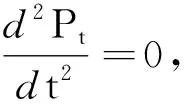
(4)

三阶导数为

(5)

(6)

根据t1，t2，t33个点，可将该曲线分为4个阶段(图1)，该阶段划分可反映新规划区负荷增长的基本规律。根据配电网规划对于饱和阶段的定义，地区负荷达到饱和的必要条件是增长率小于2%。

2.2 基于PSO改进的logistic模型法

粒子群算法(PSO)是一种随机算法，通过不断地更新迭代寻找最优解，可以很好地应用于logistic模型中各个参数的寻优。在配电网规划中，通常用负荷密度法作为预测饱和年负荷的手段，以自然增长法和点负荷法作为近期负荷预测的方法，但是自然增长法和点负荷法无法紧密联系历史负荷数据，得到的结果不符合地区负荷发展的特性，也无法得到过渡年负荷的发展曲线。本文使用改进的logistic模型进行过渡年的负荷数据预测，在已知饱和年负荷的情况下，改进后的logistic模型可以有效模拟过渡年负荷数据的变化情况，得到该地区的负荷发展曲线，且符合地区负荷发展各阶段规律。

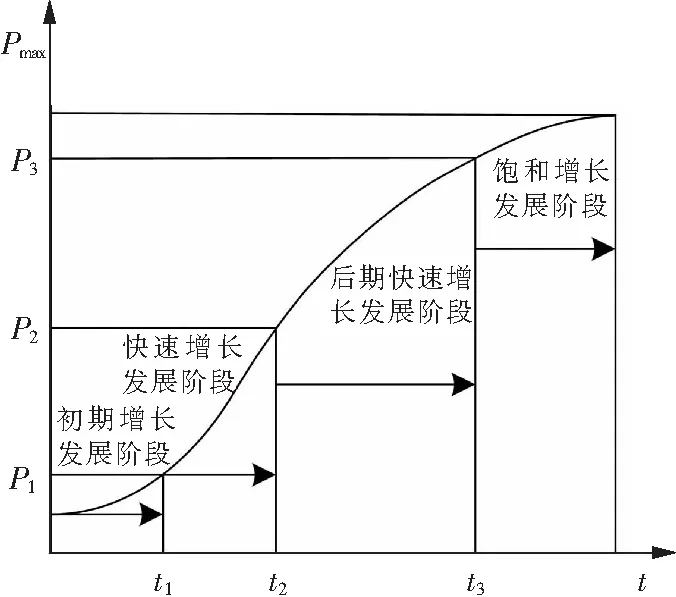
图1 logistic模型四阶段划分Fig.1 Four-stage division of logistic model

常规的logistic模型中，参数的选择一般采用最小二乘法，具有一定的误差性，参数结果不能完全反映历史数据与饱和年的负荷情况，并且，在本文中改进的logistic模型，由于加入了随机变量，常规的尤拉法、若赫茨法、耐尔法无法对各参数准确求解，本文采用PSO对历史负荷的拟合程度进行寻优，得到各参数的最优值，并使用优化过的logistic模型进行过渡年的负荷预测。

根据logistic曲线增长趋势的不同，可以将logistic模型分为4个发展阶段[24]，四阶段划分可以更加准确、合理地拟合出地区负荷发展情况。配电网负荷预测流程图如图2所示。

3 计算与分析

本文以华东某地区2001年至2020年历史负荷数据与该地区发展规划为案例，探究该地区配电网规划过程中负荷预测相关问题。

3.1 饱和负荷预测

以土地利用规划、地区发展规划、饱和期项目规划为基础，运用空间地理分布模型，将规划地区划分为各个不同的地块。根据该地区地块的划分情况，并对邻近地区与发达地区的同等类型用地的负荷密度调研，得到各地块类型负荷密度和同时率。根据式(1)，通过空间负荷密度法，计算饱和年负荷，其值为1 506 MW。

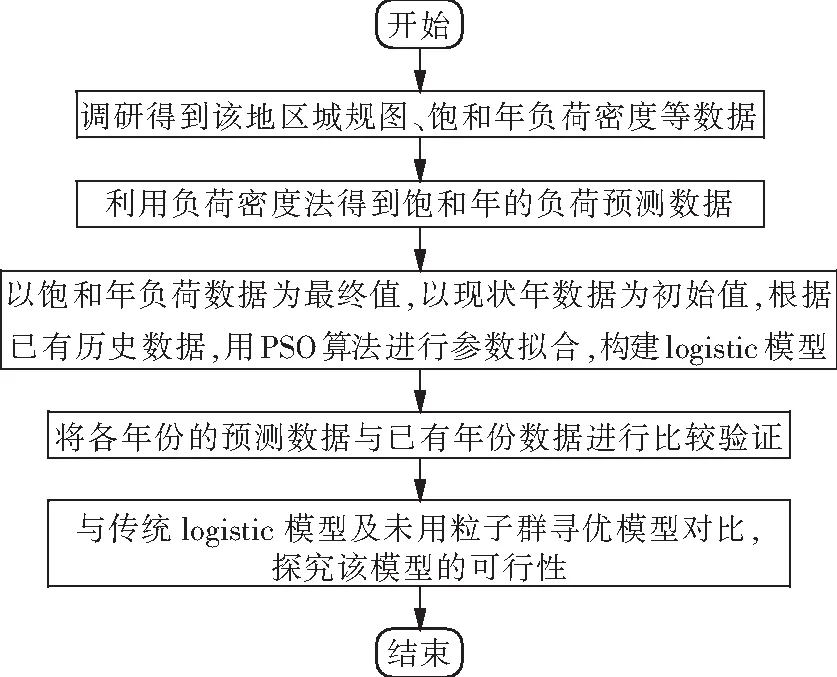
图2 配电网负荷预测流程图Fig.2 Distribution network load forecasting flow chart

3.2 过渡年负荷预测

该地区2001年至2020年历史负荷数据如表1所示，表中Pmax为年最大负荷，根据式(2)与式(3)，且P0的值确定为1 506 MW，利用粒子群优化算法，确定logistic各参数的最优值，为减小误差，分别求取10次各参数的值，取其均值作为最终预测的参数值，最优参数分别为k=7.062×10-4,a=7.973 5×105,b=7.6×10-3。拟合预测结果如图3所示。

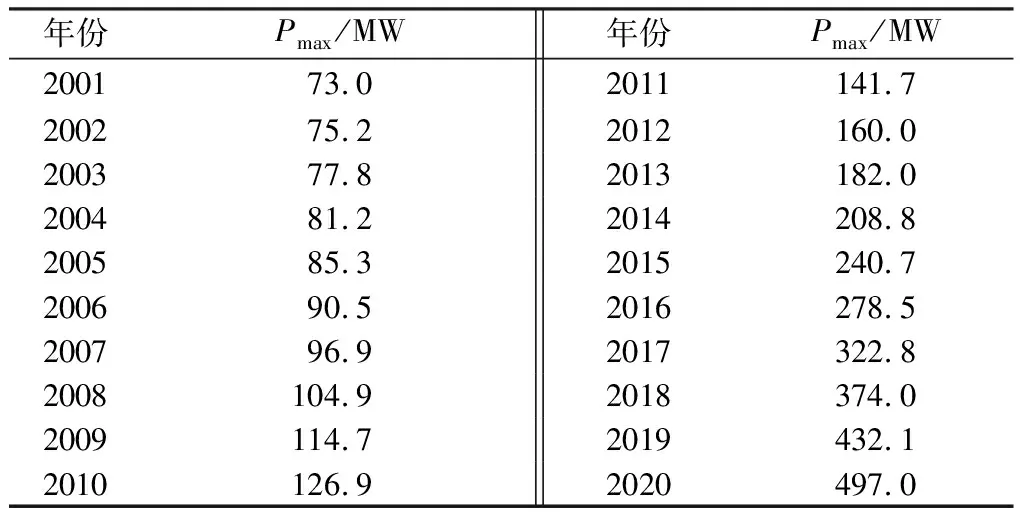
表1 历史负荷数据Tab.1 Historical load data

将该地区的年最大负荷的预测值与真实值对比可得，平均相对误差为5.12%，相对误差绝对值的平均值为ε=7.22%，则其建模精度为α=(1-ε)×100%=92.78%。

根据拟合预测结果中最大负荷增长率变化趋势，可得t1=2003，t2=2018，t3=2034，由此可认为2003年之前该地区最大负荷处于初期发展阶段，2003年到2018年处于中期发展阶段，2018年到2034年增长速度逐渐变慢，处于后期发展阶段，2034年以后逐渐进入饱和阶段。根据结果，可以得到结论，2034年为饱和年，与该地区规划基本一致。且2034年，年增长率小于2%，符合饱和阶段的必要条件。该地区负荷年增长率Pgrow如图4所示。

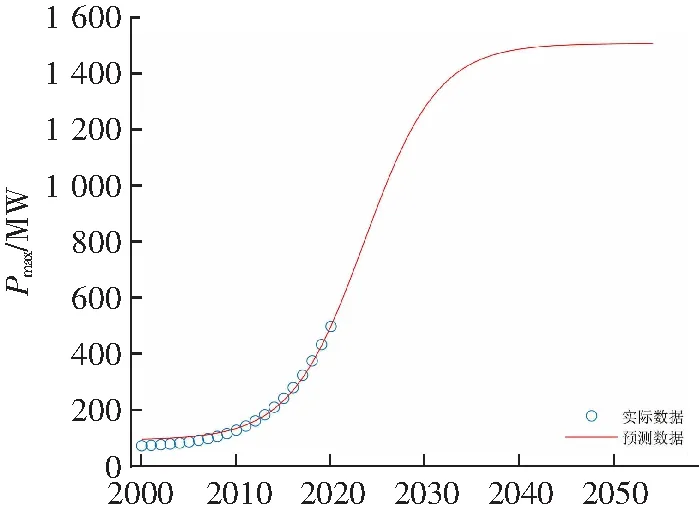
年份图3 拟合预测结果Fig.3 Fitting prediction results

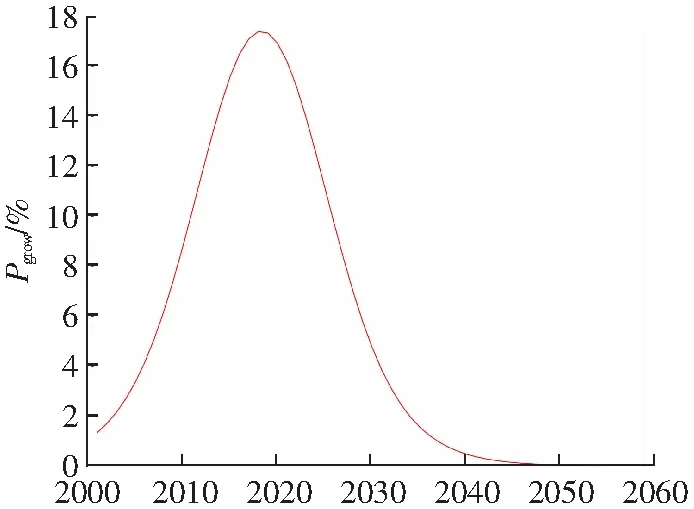
年份图4 年最大负荷增长率Fig.4 Annual maximum load growth rate

3.3 对比分析

为了体现改进logistic模型预测过渡年负荷的优越性，令该模型与传统logistic模型及未用粒子群寻优模型做对比，其中，未用粒子群寻优模型各参数采用尤拉法求取[11]。为衡量预测模型输出的预测值与实际值拟合程度的优劣，本文选择平均绝对百分比误差EMAP、均方根误差ERES、拟合优度检验R2作为评价指标，各模型拟合情况如图5所示，误差对比如表2所示。

结果表明，改进logistic模型相比于原始模型，EMAP，ERES，R2指标有所提高，且最终负荷收敛于该地区的饱和负荷。而采用PSO优化的logistic模型，各指标相比于另外两个模型均表现更好，更能精准地预测该地区的过渡年负荷。

年份图5 各模型对比Fig.5 Comparison of each model

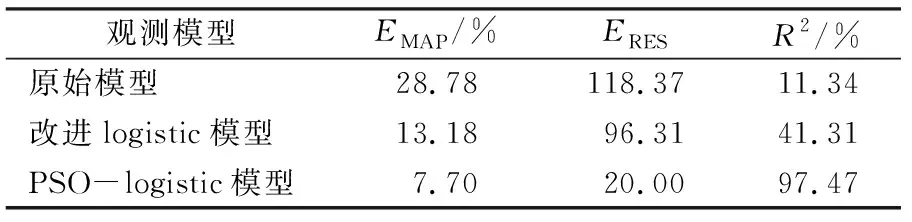
表2 各模型误差对比Tab.2 Comparison of the errors of each model

4 结论与展望

对于配电网规划中所需要的饱和年负荷预测和过渡年负荷预测，本文提出了一种基于PSO优化logistic模型的预测方法，首先利用空间密度法进行空间负荷预测，然后对logistic模型进行改进，并结合饱和负荷值与该地区历史负荷值，利用PSO对logistic模型参数进行寻优，最终得到过渡年各阶段负荷值与各阶段划分的时间节点；通过对预测值进行对比分析表明，该模型精度相对于未改进的logistic模型有所提高。综上分析，该模型可用于地区配电网规划中的负荷预测，具有一定的工程意义。