MTL∀谓词逻辑系统公理化真度的运算性质研究

王 波, 惠小静, 鲁 星

(延安大学 数学与计算机科学学院,陕西 延安 716000)

作为非经典数理逻辑的一个重要分支,模糊逻辑是逻辑系统研究的一个重要方向.受连续三角模结构定理的启发,捷克科学院院士Petr Hájek于1998年提出基本逻辑的形式系统BL[1],将BL系统弱化就形成了MTL系统.该系统是由Esteva 和Godo于2001年提出的[2],许多专家在此基础上进行研究,得到了一些研究成果[3—12].

与命题逻辑MTL系统相对应的是谓词逻辑系统MTL∀,谓词逻辑系统MTL∀包含基本命题逻辑系统MTL以及含有量词的公理.目前,计量化研究主要是在命题逻辑MTL系统中进行的[13—14],对谓词逻辑系统MTL∀进行计量化研究是一个重要课题.

命题逻辑的计量化从基本概念的程度化入手引进了命题逻辑公式真度的概念,是基于语义的方法建立的,但在谓词逻辑中其语义理论远比命题逻辑复杂,因此采用语义的方法建立真度的概念难度很大.王国俊在文献[15]中提供了一种用公理化的方法建立一阶逻辑公式的真度理论.本文在此基础上,结合谓词逻辑系统MTL∀的相关公理及定理,研究谓词逻辑系统MTL∀的公理化真度.文中首先介绍了公理化真度的概念,其次介绍了谓词逻辑系统MTL∀;最后，论证了形如((A→B)→(A→C))→(B→C)及(∀x)A→B等公式真度计算的转化方法.

1 预备知识

文献[15]采用公理化方法给出了谓词逻辑公理化真度的概念.该公理化真度具有普适性,在此基础上相关理论的展开采用严格的逻辑推理而不再借助语义理论和概率计算.由于谓词逻辑的复杂性,公理化真度是在不含函数符号的一阶闭逻辑公式中展开的.Ф表示全体不含函数符号的一阶闭逻辑公式之集,下面首先对Ф中的公式真度的定义和真度映射τ具有的性质进行说明,其中A,B,C等表示Ф中的一阶逻辑公式.

定义1[16]一阶语言由以下符号组成:

(ⅰ)变元符号:x1,x2,….

(ⅱ)个体常元符号:a1,a2,….

(ⅵ)全称量词符号:∀.

定义2[16]设Ψ是一阶语言,则Ψ中的项定义如下:

(ⅰ)变元和Ψ中的个体常元是项.

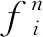
(ⅲ)Ψ中的项均由(ⅰ)与(ⅱ)的方式生成.

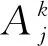
(ⅰ)原子公式是合式公式.

(ⅱ)若A与B是合式公式,则A,A→B与(∀x)A也都是合式公式.

(ⅲ)合式公式均由(ⅰ)与(ⅱ)的方式生成.

定义4[16]设A(xi)是含有变元xi的公式,t是一个项.若下列条件之一满足，则称t关于A(xi)中的xi是自由的:

(ⅰ)xi不是A(xi)中的自由变元；

(ⅱ)xi是A(xi)中的自由变元且t中的变元在A(t)中都是自由变元.

定义5[16]一阶语言Ψ中不含自由出现的变元的公式称为闭公式.

定义6[16]Ψ中的原子公式及其否定称为文字.设x1,…,xn是公式A中的全部自由出现的变元,则称(∀x1)…(∀xn)A为A的完全闭包,记作clA.

定义7[15]称映射τ:Ф→[0,1]为公理化真度映射,若以下条件成立:

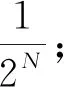
(K2) 若A是Ф中的定理,则τ(A)=1；

(K3)τ(A)=1-τ(A),A∈Ф；

(K4)τ(A→B)+τ(A)=τ(B→A)+τ(B),A,B∈Ф；

(K5)τ(cl(A))=1-τ(clA)；

(K6) 在计算公式的真度时,其中原子公式中的变元可相互替换.

以定义7为基础,文献[15]中证明了公理化真度具有如下性质.

命题1[15]真度映射τ具有以下性质:

(ⅰ) 若A是矛盾式,则τ(A)=0；

(ⅱ) 若A与B是逻辑等价,则τ(A)=τ(B)；

(ⅲ) 若τ(A→B)=1,则τ(A)≤τ(B)；

(ⅳ) 若τ(A)≥a,τ(A→B)≥b,则τ(B)≥a+

b-1；

(ⅴ) 若τ(A→B)≥a,τ(B→C)≥b,则τ(A→C)≥a+b-1；

(ⅵ)τ(A→C)≥τ(A→B)+τ(B→C)-1；

(ⅶ)τ(A∨B)+τ(A∧B)=τ(A)+τ(B).

接下来介绍谓词演算系统MTL∀的公理和部分定理.

定义8[3]谓词演算系统MTL∀的公理为MTL的10条公理再加上关于量词的公理.

(ⅰ) 命题演算系统MTL的公理:

(MTL1) (A→B)→((B→C)→(A→C))；

(MTL2)A&B→A；

(MTL3)A&B→B&A；

(MTL4)A∧B→A；

(MTL5)A∧B→B∧A；

(MTL6)A&(A→B)→(A∧B)；

(MTL7a) (A→(B→C))→(A&B→C)；

(MTL7b) (A&B→C)→(A→(B→C))；

(MTL8) ((A→B)→C)→(((B→A)→C)→C)；

(MTL9) 0→A.

(ⅱ)带有量词的公理:

(∀1)(∀x)A(x)→A(t),其中项t对于A(x)中的x可替换；

(∃1)A(t)→(∃x)A(x),其中项t对于A(x)中的x可替换；

(∀2)(∀x)(A→B)→(A→(∀x)B),其中x在A中不自由出现；

(∃2)(∀x)(A→B)→((∃x)A→B),其中x在B中不自由出现；

(∀3)(∀x)(A∨B)→((∀x)A∨B),其中x在B中不自由出现.

系统MTL∀的推理规则:

MP规则[3]: 由A,A→B推出B.

推广规则[3]: 由A推出(∀x)A.

HS规则[2]:A→B,B→C可得A→C.

定理1[3]以下公式在MTL∀中可证:

(ⅰ)(A→(B→C))→(B→(A→C))；

(ⅱ)A→A；

(ⅲ)(∀x)(A∧B)≡((∀x)A∧(∀x)B)；

(ⅳ) (∃x)(C→A)→(C→(∃x)A)，其中x在C中不自由出现.

(ⅴ) (∃x)(A→C)→((∀x)A→C)，其中x在C中不自由出现.

2 MTL∀系统的公理化真度计算转化方法

本节将在公理化真度定义7的基础上结合谓词演算系统MTL∀,研究MTL∀系统中公理化真度,给出了真度计算的转化公式.以下讨论均在Ф中展开,即A,B,C均为不含函数符号的闭公式.

定理2

τ(((A→B)→(A→C))→(B→C))=

τ(B→C)-τ((A→B)→(A→C))+1.

证明首先证明(B→C)→((A→B)→(A→C))为定理:

(ⅰ)由(MTL1)得(A→B)→((B→C)→(A→C)).

(ⅱ)由定理1(ⅰ)得

((A→B)→((B→C)→(A→C)))→

((B→C)→((A→B)→(A→C))).

(ⅲ)由(ⅰ),(ⅱ)及MP得(B→C)→((A→B)→(A→C)).

由(K2)知τ((B→C)→((A→B)→(A→C)))=1.由(K4)知

τ(((A→B)→(A→C))→(B→C))+

τ((A→B)→(A→C))=

τ((B→C)→((A→B)→(A→C)))+τ(B→C).

所以

τ(((A→B)→(A→C))→(B→C))=

τ(B→C)-τ((A→B)→(A→C))+1.

注1可见,形如((A→B)→(A→C))→(B→C)公式的真度可通过转化为(B→C)与((A→B)→(A→C))的真度进行计算,下面举例论证.

例1计算

τ((((∀x)A→(∀x)A)→((∀x)A→

的值.

解由定理2知

τ((((∀x)A→(∀x)A)→

((∀x)A→(∃x)A))→

((∀x)A→(∃x)A))=

τ((∀x)A→(∃x)A)-

τ(((∀x)A→(∀x)A)→

((∀x)A→(∃x)A))+1.

由定理1(ⅲ)知(∀x)A→(∃x)A是定理. 由(K2)知

τ((∀x)A→(∃x)A)=1.

(1)

由定理2(ⅲ)知(B→C)→((A→B)→(A→C))为定理,因此,同理可证

((∀x)A→(∃x)A)→

(((∀x)A→(∀x)A)→((∀x)A→(∃x)A))

是定理.由(K2)知

τ(((∀x)A→(∃x)A)→(((∀x)A→

(∀x)A)→((∀x)A→(∃x)A)))=1.

由命题1(ⅲ)知

τ((∀x)A→(∃x)A)≤τ(((∀x)A→

(∀x)A)→((∀x)A→(∃x)A)).

由于0≤τ(((∀x)A→(∀x)A)→((∀x)A→(∃x)A))≤1，由 (1) 式知τ((∀x)A→(∃x)A)=1.从而τ(((∀x)A→(∀x)A)→((∀x)A→(∃x)A))=1.所以

τ((((∀x)A→(∀x)A)→

((∀x)A→(∃x)A))→

((∀x)A→(∃x)A))=1-1+1=1，

即τ((((∀x)A→(∀x)A)→((∀x)A→(∃x)A))→

((∀x)A→(∃x)A))的取值为1.

定理3τ(A)=τ((∀x)A).

证明首先证明A→(∀x)A是定理:

(ⅰ) 由定理1(ⅱ)得A→A；

(ⅱ)由(ⅰ)和推广规则得(∀x)(A→A)；

(ⅲ)由 (∀2)得(∀x)(A→A)→(A→(∀x)A)，其中x在A中不自由出现；

(ⅳ)由(ⅱ),(ⅲ)及MP得A→(∀x)A.

由(K2)知τ(A→(∀x)A)=1.由命题1(ⅲ)知τ(A)≤τ((∀x)A).由公理(∀1)及(K2)知τ((∀x)A→A)=1.由命题1(ⅲ)知τ((∀x)A)≤τ(A).所以τ(A)=τ((∀x)A).

定理4τ((∀x)((∀x)A∨(∀x)B))=τ((∀x)A∨(∀x)B).

证明首先证明(∀x)((∀x)A∨(∀x)B)→(∀x)A∨(∀x)B为定理.由(∀1)得

(∀x)((∀x)A∨(∀x)B)→(∀x)A∨(∀x)B.

由(K2)知τ((∀x)((∀x)A∨(∀x)B)→(∀x)A∨(∀x)B)=1.由命题1(ⅲ)知

τ((∀x)((∀x)A∨(∀x)B))≤τ((∀x)A∨(∀x)B).

接下来证明(∀x)A∨(∀x)B→(∀x)((∀x)A∨(∀x)B)为定理.由定理3(ⅳ)得

(∀x)A∨(∀x)B→(∀x)((∀x)A∨(∀x)B).

(2)

(2)式与定理3(ⅳ)中A→(∀x)A形式相同.由(K2)知

τ((∀x)A∨(∀x)B→(∀x)((∀x)A∨(∀x)B))=1.

由命题1(ⅲ)知

τ((∀x)A∨(∀x)B)≤τ((∀x)((∀x)A∨(∀x)B)).

所以τ((∀x)((∀x)A∨(∀x)B))=τ((∀x)A∨(∀x)B).

注2由定理1(ⅲ)知τ((∀x)(A∧B))=τ((∀x)A∧(∀x)B).可见交与并的分配对于真度的关系式二者是有差别的.

定理5τ(A→(∀x)B)=τ((∃x)A→B).

证明首先证明(A→(∀x)B)→(∀x)(A→B)为定理.

(ⅰ) 由(∀1)得(∀x)B→B.

(ⅱ) 由定理2(ⅲ)得

((∀x)B→B)→((A→(∀x)B)→(A→B)).

(3)

(3)式与定理2(ⅲ)中(B→C)→((A→B)→(A→C))形式相同.

(ⅲ)由(ⅰ),(ⅱ)及MP得(A→(∀x)B)→(A→B).

(ⅳ)由定理3(ⅳ)得

(A→B)→(∀x)(A→B).

(4)

(4)式与定理3(ⅳ)中A→(∀x)A形式相同.

(ⅴ) 由(ⅲ),(ⅳ)及HS得 (A→(∀x)B)→(∀x)(A→B).

由(K2)知τ((A→(∀x)B)→(∀x)(A→B))=1.由命题1(ⅲ)知

τ(A→(∀x)B)≤τ((∀x)(A→B)).

由(∀2)及(K2)知

τ((∀x)(A→B)→(A→(∀x)B))=1.

由命题1(ⅲ)知

τ((∀x)(A→B))≤τ(A→(∀x)B).

所以τ(A→(∀x)B)=τ((∀x)(A→B)).

接下来证明((∃x)A→B)→((∀x)(A→B))是定理.

(ⅰ)由(∃1)得A→(∃x)A.

(ⅱ)由(MTL1)得

(A→(∃x)A)→(((∃x)A→B)→(A→B)).

(ⅲ) 由(ⅰ),(ⅱ)及MP 得

((∃x)A→B)→(A→B).

(ⅳ) 由定理3(ⅳ)得

(A→B)→(∀x)(A→B).

(5)

(5)式与定理3(ⅳ)中A→(∀x)A形式相同.

(ⅴ) 由(ⅲ),(ⅳ)及HS 得

((∃x)A→B)→(∀x)(A→B).

由(K2)知τ(((∃x)A→B)→(∀x)(A→B))=1.由命题1(ⅲ)知

τ((∃x)A→B)≤τ((∀x)(A→B)).

由(∃2)及(K2)知τ((∀x)(A→B)→((∃x)A→B))=1.由命题1(ⅲ)知

τ((∀x)(A→B))≤τ((∃x)A→B).

所以τ((∀x)(A→B))=τ((∃x)A→B)，从而τ(A→(∀x)B)=τ((∃x)A→B).

定理6τ((∀x)A→B)=τ(A→(∃x)B).

证明首先证明(B→(∃x)A)→((∃x)(B→A))是定理.

(ⅰ)由定理1(ⅱ)得A→A.

(ⅱ)由(ⅰ)及推广规则得(∀x)(A→A).

(ⅲ)由(∃2)得(∀x)(A→A)→((∃x)A→A)，其中x在A中不自由出现.

(ⅳ) 由(ⅱ),(ⅲ)及MP 得(∃x)A→A.

(ⅴ)由定理2(ⅲ)得

((∃x)A→A)→((B→(∃x)A)→(B→A)).

(6)

(6)式与定理2(ⅲ)中(B→C)→((A→B)→(A→C))形式相同.

(ⅵ) 由(ⅳ),(ⅴ)及MP得

(B→(∃x)A)→(B→A).

(ⅶ) 由(∃1)得(B→A)→(∃x)(B→A).

(ⅷ)由(ⅵ),(ⅶ)及HS得

(B→(∃x)A)→(∃x)(B→A).

由(K2)知τ((B→(∃x)A)→(∃x)(B→A))=1.由命题1(ⅲ)知

τ(B→(∃x)A)≤τ((∃x)(B→A)).

由定理1(ⅳ)及(K2)知

τ((∃x)(B→A)→(B→(∃x)A))=1.

由命题1(ⅲ)知

τ((∃x)B→A)≤τ(B→(∃x)A).

所以τ((∃x)(B→A))=τ(B→(∃x)A).

接下来证明((∀x)A→B)→((∃x)(A→B))是定理.

(ⅰ) 由定理3(ⅳ)得

A→(∀x)A.

(7)

(7)式与定理3(ⅳ)中A→(∀x)A形式相同.

(ⅱ)由(MTL1)得

(A→(∀x)A)→(((∀x)A→B)→(A→B)).

(ⅲ) 由(ⅰ),(ⅱ)及MP得

((∀x)A→B)→(A→B).

(ⅳ) 由(∃1)得

(A→B)→(∃x)(A→B).

(ⅴ) 由(ⅲ),(ⅳ)及HS得

((∀x)A→B)→(∃x)(A→B).

由(K2)知τ(((∀x)A→B)→(∃x)(A→B))=1.由命题1(ⅲ)知

τ((∀x)A→B)≤τ((∃x)(A→B)).

由定理1(ⅴ)及(K2)知τ((∃x)(A→B)→((∀x)A→B))=1.由命题1(ⅲ)知τ((∃x)(A→B))≤τ((∀x)A→B).所以τ((∀x)A→B)=τ((∃x)(A→B))，从而τ((∀x)A→B)=τ(A→(∃x)B).

注3定理5和定理6给出了∃与∀之间真度的相互转化关系,方便后续学者计算真度.

例2计算τ(A)+τ(B)的值.

解由(K4)知

τ((∀x)A→B)+τ((∀x)A)=

τ(B→(∀x)A)+τ(B).

由定理5知τ(B→(∀x)A)=τ((∃x)B→A)，所以

τ((∀x)A→B)+τ((∀x)A)=

τ((∃x)B→A)+τ(B).

由定理6知τ((∀x)A→B)=τ(A→(∃x)B)，所以

τ(A→(∃x)B)+τ((∀x)A)=

τ((∃x)B→A)+τ(B).

由(K4)知

τ(A→(∃x)B)+τ(A)=

τ((∃x)B→A)+τ((∃x)B)，

所以

τ(A→(∃x)B)=

τ((∃x)B→A)+τ((∃x)B)-τ(A)，

从而

τ((∃x)B→A)+τ((∃x)B)-τ(A)+

τ((∀x)A)=τ((∃x)B→A)+τ(B).

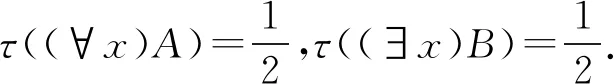
3 结语

本文在文献[15]的基础上研究了谓词演算系统MTL∀的公理化真度及其一些运算性质.笔者将在另文中讨论以公理化真度为基础建立逻辑度量空间并展开相容度及发散度等相关问题.