基于混合故障率的设备分阶段顺序维修决策优化研究

吴耀胜，刘勤明，叶春明

(上海理工大学 管理学院，上海 200093)

随着社会的发展，对于设备可靠性的要求越来越高，对设备制定合理的维修策略可以有效地增加企业的竞争力，由于设备故障带来的生产线停产会使企业的利润减少，甚至会使企业遭受巨大的损失，所以对设备制定有效的维护计划具有重要的意义。

设备维护是企业运营管理的重要内容之一，进行有效、科学的维修活动可以有效降低企业的运营成本，增加企业的盈利能力。Zhou等[1]提出一种以可靠性为中心的维修策略，通过引入役龄递减因子与故障率递增因子建立基于设备可靠性的预防性维修模型，最后讨论不同的成本参数对维修策略的影响。Malik[2]和Nakagawa等[3]先后通过利用等效役龄与故障率递增来描述设备在维修前后的故障率变化，给单设备预防性维护建模提供基本方案。Ahmad[4]和Le等[5]分别基于设备维修成本和可靠性建立了非周期预防性维修优化模型，并对模型进行求解。金玉兰等[6]以多部件设备为研究对象，提出非等周期维修策略，运用马尔可夫过程建立不同维修策略的转移概率表达式，解决组合的预防维修策略问题。韩帮军等[7]在小修的基础上加入预防性维修，建立顺序性预防性维修模型。邓超等[8]将设备的退化过程进行分段，并对维修资源进行分类，提出分阶段顺序维修模型。石慧等[9]考虑设备寿命为维修阙值的预防性维护策略，利用微粒群算法对预防性维修模型进行求解，使平均费用最小。张斌等[10]考虑退化和随机冲击对系统可靠度的影响，构建预防性维修模型并引入役龄回退因子，建立费用率函数最小的目标函数，并分析参数对维修策略的影响。宋之杰等[11]建立等周期维修模型，以考虑动态成本和可用度为约束为条件。王灵芝等[12]建立多部件成组维修优化模型，以系统可靠度最大化和维修费用最小化为目标函数。

然而，很多文献[13-18]没有考虑设备维修成本的动态性以及改善因子的可变性，本文采用混合故障率函数，综合考虑动态的役龄改善因子及故障率递增因子对故障率的影响。随着设备逐渐老化和故障逐渐增多，考虑现实的可操作性，本文为了避免等周期维修的不实际性以及非等周期的不易操作性，根据设备退化过程不同的特征，将维修阶段分成不同的3个阶段，在每个阶段内进行等周期维修，这样更具有可操作性。本文以总的费用率为目标函数，一定的可靠度为约束条件以保证设备的可靠运行，建立分阶段等周期的维修优化模型。

1 问题描述

设备维修的方式一般有小修、不完全维修和更换3种。本文考虑设备的退化过程中的不同特性，将设备的维修过程分成3个不同的阶段，每个阶段的维护间隔都为固定的时间，如表1所示。其中，阶段1表示设备在刚开始运行的一段时间内状态良好，具有较低的故障率；阶段2表示设备在运行一段时间后，状态变差，故障率也出现增加的趋势；阶段3表示设备经过长时间运行，状态比较差，故障经常发生，需进行多次预防性维修。

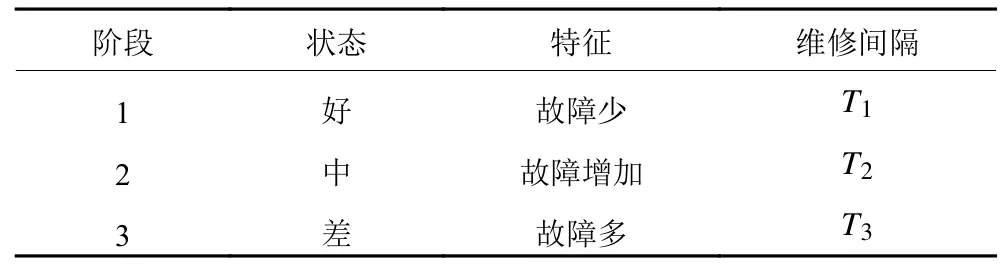
表1 顺序维修不同阶段的特征Table 1 Characteristics of different stages of sequential maintenance

根据分析3个阶段设备的退化特点，将维修过程分成不同的3个阶段。

分阶段顺序维修决策步骤如下。

1) 根据设备在生命周期内退化的不同特性，将维修阶段分成3个不同的阶段，在每阶段进行N1、N2和N3次预防性维修。

2) 在每个阶段有固定的维修时间，每个阶段的维修时间分别是T1、T2和T3。

3) 在每个预防性周期若发生故障则进行小修，每个预防性周期结束后进行不完全维修，3个阶段维护结束后对设备进行预防性更换。

在维修3个阶段中的各个维护周期内，为了保证设备的正常运行，需要可靠度在一定的数值之上。

2 符号说明和模型假设

2.1 符号说明

cf：固定成本；

cv：可变成本；

Cr：更换成本；

Tr：更换时间；

a：设备维修成本的调整参数；

b：为不完全维修次数的调整参数；

Ti：第i次维护间隔时间；

Cm：小修费用；

tm：小修时间；

tpmi：第i次预防性维修所需要的时间；

Cp：单位时间停机损失；

N1：第1阶段维护次数；

N2：第2阶段维护次数；

N3：第3阶段维护次数；

λ(t)：故障率函数；

αi：第i次不完全维修的役龄改善因子；

bi：故障率递增因子。

2.2 模型假设

1) 在维护期内设备如果发生故障，则对设备进行小修，小修的时间和成本都是不变的。

2) 在每个维护周期结束后，对设备采用不完全维修方式，通过引入改善因子描述设备故障率的变化，不完全维修的维修时间和维修成本是随着维修次数的增加而逐渐增加。

3) 对设备进行更换是在最后一个维护周期结束后进行，更换时间和成本是一定值。

3 动态不完全预防性维修模型的构建

3.1 动态不完全维修成本

由于设备在运行中状态不断退化，要使设备正常运作，设备的可靠性保证在一定的范围内，维修成本是逐渐增加的。本文中的不完全维修成本是一个动态成本，它是由固定成本cf和可变成本cv组成，即不完全维修成本可以表示为

其中，i表示第i次不完全维修。随着设备的不完全维修次数的增加，每次的不完全维修成本也在逐渐增加。

3.2 混合故障率函数

考虑设备不完全维修会使设备的役龄回退，运行时间的增加会使设备的故障率增加，所以本文通过役龄改善因子来描述经过第i次预防性维修的故障率函数的变化，设备的故障率函数变为

其中，αi为役龄改善因子，0＜αi＜1。再次引入故障率递增因子bi，

从而得到混合故障率函数为

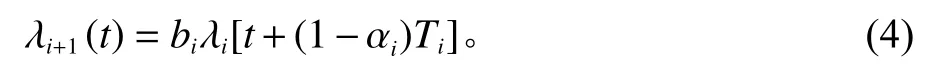
其中，故障率役龄改善因子为

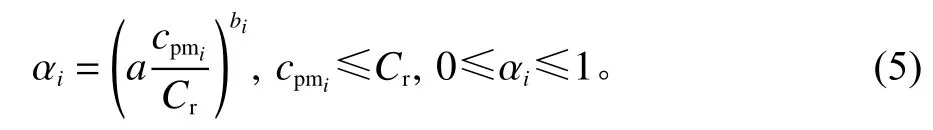
式中，i表示不完全维修次数；0＜a＜。

设备在第i个预防性维护周期中的可靠度函数为

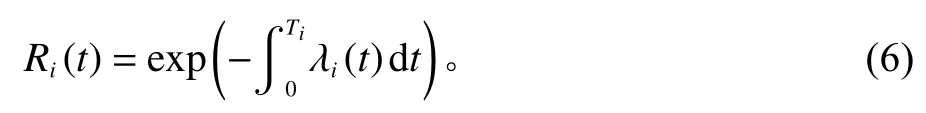
通过引入役龄改善因子，设备在第i次预防性维修中的故障率函数λi(t)可以得到

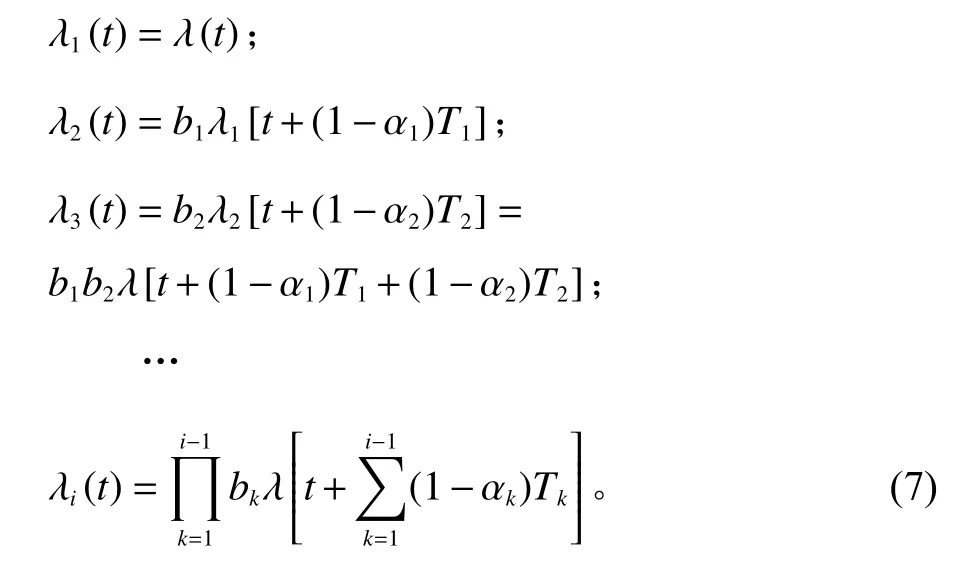
为了保证设备正常运行，设备的可靠度应该满足

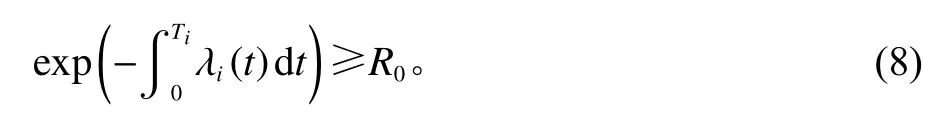
其中，Ti为维修间隔时间，i=1,2,3,···,N。

3.3 设备维护成本

设备在维护期内发生故障需进行小修会产生小修成本，预防性维修会有动态的维修成本，对设备更换时会有更换成本，还有停机会产生停机成本。

1) 若设备在预防性维护期内发生故障，则采用小修方式进行维修。

设备总的小修费用为

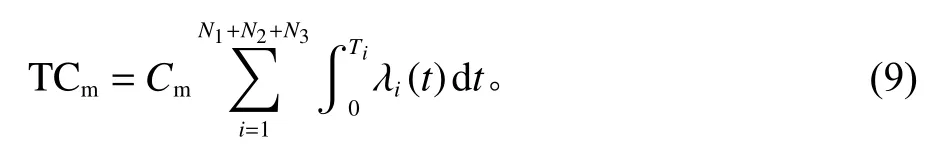
设备小修总时间

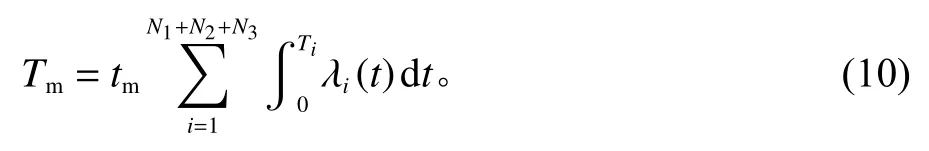
2)当运行时间达到维修间隔时间时对设备进行预防性维修。设备的预防性维修成本是随着维修次数而逐渐变化的，设备在生命期总的预防性维修成本为

设备在第i次预防性维修所需要的时间为tpmi=。其中，k是时间调整因子。总的预防性维修时间为

3) 设备的更换成本是Cr，设备的更换时间为Tr。

4) 停机损失成本。停机总时间为

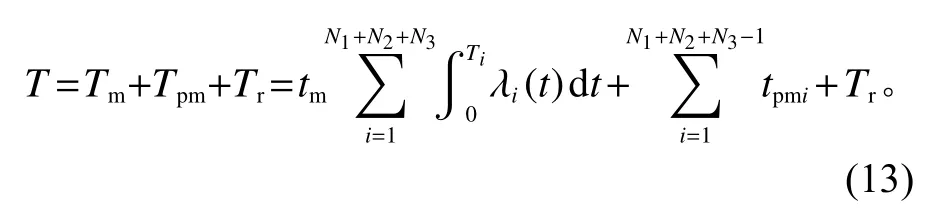
设备停机总成本为Cs=CpT。其中，Cp为单位时间停机损失。

设备总的维修成本为

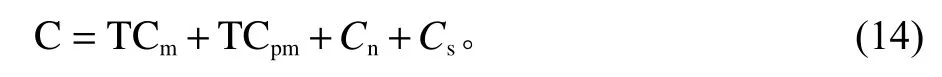
3.4 分阶段顺序维修模型

以总费用率最小为优化目标，一定的可靠度为约束条件，建立分阶段顺序维修模型。

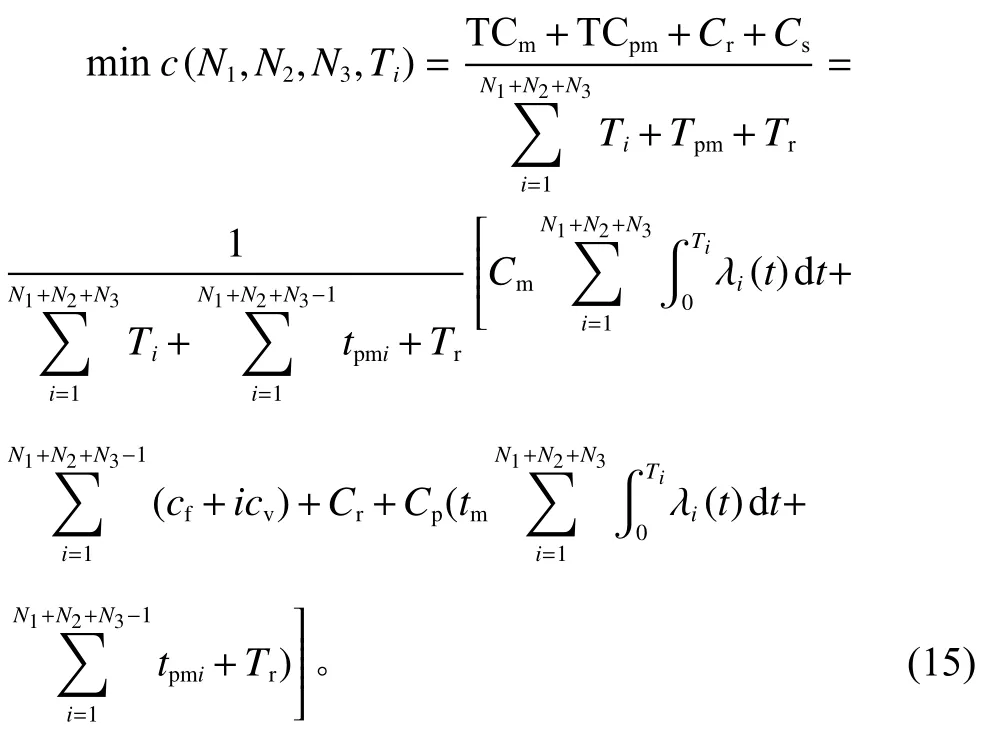
式中，N1、N2、N3、Ti为决策变量，并满足下面约束条件

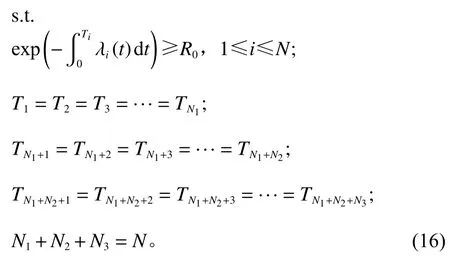
4 实例分析

为了验证模型的有效性，给出以下实例进行分析。假设某生产设备的故障率服从 β=3，η=190的威尔布分布，即λ(t)=,t≥0。模型中的参数分别为cf=6 000，cv=200，Cm=7 000，Cp=4 000，Cr=600 000，tm=0.5d,Tr=1.5d，a=0.3，b=0.5，bi=1.1，k=3，Cn=5 000，Cpm=8 000，R0=0.85。

4.1 求解步骤

1) 代入相关参数值，使N=N1+N2+N3=3；

2) 使N1、N2、N3取值为正整数，利用 Matlab中的非线性约束优化工具进行求解，得到维修间隔期为T∗时间的最小费用率C∗和最优的预防性维护次数N1∗、N2∗、N3∗；

3) 令N=N+1，用同样的方法再次求解此时的T*和C∗，并比较C∗(N)和C∗(N−1)；

4) 如果C∗(N)＜C∗(N−1)，转至第3步，否则，输出N∗=N−1时的T*和N1∗、N2∗，N3∗，即为各个阶段的最优维护次数。

4.2 结果分析

图1反映了3个阶段不同的维修次数与费用率之间的关系。由图1可得费用率随着维修次数的增加先减少后增加，当N=10时费用率最小，即3个阶段预防性维修次数分别为N1=3次，N2=4次，N3=3次，最小费用率为900.32元/d。

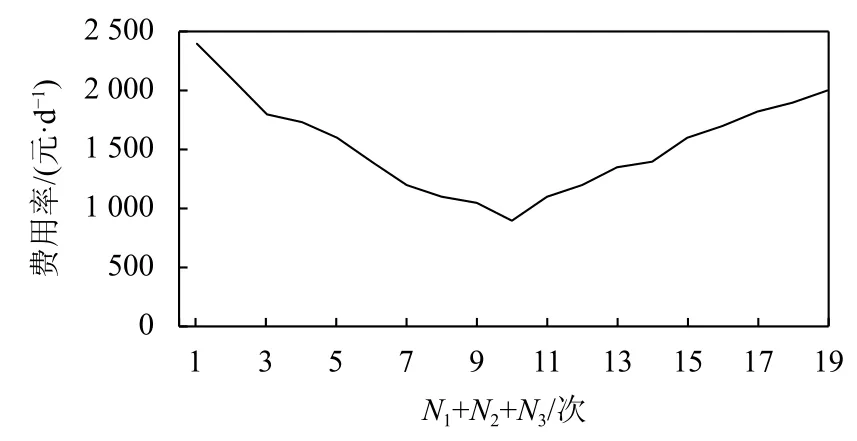
图1 预防性维修次数与费用率的关系Figure 1 The relationship between the number of preventive maintenance and the cost rate

此时的预防性维修间隔期如表2所示。设备在运行时间越来越长的情况下，发生故障的概率逐渐增加，所以维修间隔时间缩短。在保证设备可靠性大于0.85的情况下，设备寿命周期为745.977 d。

表2 最小费用率时的维修间隔期TiTable 2 Maintenance interval Ti at minimum cost rate d

考虑不同可靠度约束对模型的影响，本文的可靠度下限值为0.85。为了分析不同的可靠度下限对模型的影响，可靠度下限分别取0.7、0.75、0.8、0.85、0.9、0.95。设备费用率的变化规律如图2所示。可靠度下限值在0.85到0.9之间费用率变化较大。设备所需要可靠度较大时，需要频繁的维修以致带来较高的维修费用。当可靠度下限值低于0.85时，由于设备的可靠性要求不是很高，相应的费用率变化不是十分明显。

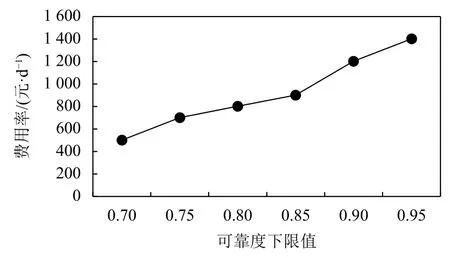
图2 不同可靠度下的费用率Figure 2 Expense rate under different reliability

4.3 结果比较

为验证本文提出模型的有效性，与一般顺序维修模型进行比较，一般顺序维修模型是在设备的生命周期内，每隔时间Ti后进行预防性维修，直到进行N-1次预防性维修，在第N次周期后对设备进行更换。在每个维护周期内如果发生故障则进行小修。

一般顺序维修策略的费用率函数为

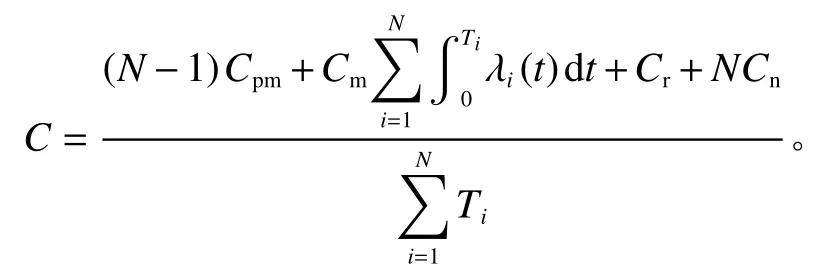
式中，Cpm为一次预防性维修费用；Cm为小修费用；Cr为更换费用；Cn为停机损失成本；λi(t)为故障率函数；Ti为第i个维修的间隔期。

对一般顺序模型进行求解，结果如图3所示。一般顺序维修模型的最佳维修次数是12次，维修间隔从107.932到38.232依次递减，设备的整个生命周期长度是814.616 d；而分阶段顺序维修的最佳维修次数是10次，设备的整个生命周期长度为745.977 d，虽然设备的生命周期缩短，但是最佳维修次数减少，可以有效地减少维修费用。这表明一般顺序维修模型可以将设备的可靠度保持在要求的范围内，但是由于后期设备维修的频繁性，会导致维修费用的增加和相应的停机损失，然而分阶段顺序维修模型可以克服这个缺点，既具有经济性也具有现实可操作性。

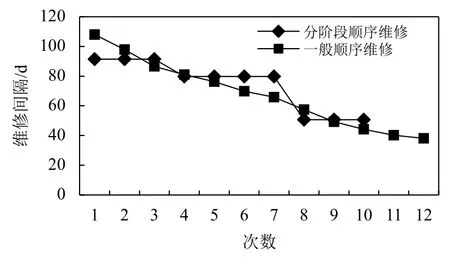
图3 模型的维修次数和维修间隔Figure 3 The number of repairs and repair intervals of the model

两种模型优化结果对比：一般顺序维修的最小费用率1 132.45元/d，而分阶段顺序维修的的最小费用率为900.32元/d，所以分阶段顺序优化模型在一定程度上来说降低了最小费用率。分阶段维修模型避免设备后期由于高故障率而进行频繁的维修策略，较少的最佳维修次数可以减少维修的费用。因此，分阶段顺序维修模型更加适合实际维修过程中的应用。

再次比较一下一般顺序维修策略和分阶段顺序模型在可靠度分别为0.75、0.8、0.85、0.9、0.95下的费用率差别。结果如图4所示。在相同可靠度条件下，分阶段顺序维修模型优于一般顺序维修模型，因为一般顺序维修在设备运行较长时间后，故障率的增加，故障出现的频率增加，从而频繁地进行维修，造成停机损失费用，所以导致其维修费用率大于分阶段顺序维修。从图4中可见，分阶段顺序维修模型的费用率比一般顺序维修模型更加节约维修费用，节约费用大约为10%～20%。因此分阶段顺序维修模型更具有经济性和实际操作性。

图4 不同维修策略费用率的对比Figure 4 Comparison of cost rates of different maintenance strategies

5 结论

本文考虑设备维修成本的动态性和改善因子的可变性，以及传统等周期维护的不实际性和弹性维护周期的操作性的难度，提出基于混合故障率的分阶段顺序维修优化模型，综合考虑突发性故障成本、预防性维修成本、更换成本和停机损失成本等成本，以总费用率最小为目标函数，得出相应的每个阶段的预防性维修次数与每个阶段的预防性维修时间。分阶段顺序维修优化模型既能使总的费用率最小化，也能保证设备的可靠度和实际操作中的可行性。