基于绿色生产的混合流水车间调度问题研究
2022-07-15唐红涛
唐红涛,张 缓
(武汉理工大学 1.机电工程学院;2.湖北省数字制造重点实验室,湖北 武汉 430070)
混合流水车间调度问题(hybrid flow-shop scheduling problem,HFSP)[1]是一种最基本的调度问题。在HFSP问题中,加工机器的选择具有一定的柔性,这使问题规模和求解难度较一般的流水车间调度问题更大,已被证明是NP-hard问题[2]。
砂型铸造作为高能耗高污染的制造业之一[3],由于生产过程的复杂性,其相关研究较少。Bewoor等[4]将铸造车间调度问题描述为无等待约束的流水车间调度问题。铸造生产过程中材料和动力消耗大,工艺过程复杂,所需设备品种繁多。高温、高尘、高噪的生产环境直接影响车间工人的身体健康,因此对铸造车间的粉尘、噪声进行控制,尽可能节约能源的消耗,完成节能减排的目标是现代铸造业生产的主要任务之一[5]。Wu等[6]根据机器运行状态的差异性,提出一种计算不同状态下机器能耗的能量消耗模型。Kim等[7]提出能耗强度分解的方法对碳排放进行分析,构建铸造过程中CO2排放计算公式。郑军等[8]使用砂型铸造生产过程的碳效率模型和评价方法对碳排放量在一定标准内进行评估。尹瑞雪等[9]利用铸造生产系统碳排放估算与评价边界的方法,通过碳排放评估函数计算砂型铸造生产过程中的碳排放量。机械制造过程都伴随着噪声。最具有危害性的工业噪音一般可分为4类:连续的机械噪音、由高速重复的动作产生的强烈的声音、流动引起的噪音和机器加工时对工件的冲压撞击产生的噪音。与熔炉相关的燃烧过程,与冲孔过程,电机、发电机和其他机电设备相关的冲击噪声等都是工业环境产生噪声的振动源的典型实例[10]。Lu等[11]考虑噪声污染以及更常见的能源消耗和生产率问题,建立多目标无线传感器网络的数学模型,用于解决焊接车间调度问题。Lu等[12]针对HFS车间生产效率低、能耗高和噪声污染大的情形,构建一个多目标混合整数规划模型,并提出一种量化节能降噪策略以求解该模型。
由于生产过程的复杂性,砂型铸造绿色可持续生产的研究较少,将噪声这一污染作为优化目标的探索更少。因此,本文建立以最大完工时间、碳排放以及噪声为优化目标的混合流水车间调度模型,并提出一种混合离散多目标帝国竞争算法(hybrid discrete multi-objective imperial competition algorithm,HDMICA)对模型进行求解。运用一种新的初始化策略改善算法的性能,采用新途径进行帝国竞争,合理均衡帝国势力值。最后通过大量实验验证所提算法的有效性。
1 问题研究及数学模型构建
1.1 问题描述
本文研究基于绿色的混合流水车间调度问题。该问题描述如下。n个工件J={J1,J2,···,Jn}需要在m个加工资源M={M1,M2,···,Mm}上加工,任意工件Ji都有ni道工序Oi=,且每个工件的工序具有相同的加工顺序,每道工序都有一个加工资源集Mij=,Mij⊆M,工件的每道工序可以由Mij中的任意一个加工资源加工。模型建立之前作出如下假设。
1) 工件加工之前所有机器均已开机并处于空闲状态;
2) 每个工件的工序加工顺序不可改变;
3) 任一时刻,工件的每道工序最多只能在一个加工资源上加工,且每个加工资源任一时刻最多只能加工一道工序;
4) 加工过程不允许中断,每个工件在加工时必须连续加工。
1.2 模型构建
1) 符号与参数。
n为待加工工件总数;m为总的加工资源数;s为加工阶段数,即工件的工序总数;i,i'为工件序号,i,i′=1,2,···,n;j,j'为工序序号,j,j′=1,2,···,s;k为加工资源序号,k=1,2,···,m;Oij为工件i的第j道工序;Mij为工件i阶段j可选加工资源集;Cijk为工件i的阶段j在加工资源k上的加工时间;Stij为工件i的阶段j开始加工的时间;Etij为工件i的阶段j加工结束时间;Ci为工件i的最早完成时间;Pk为加工资源的工作功率;Be为电力标准折煤系数,0.122 9 kgce/(kW·h),kgce是能量消耗量;EFe为电能的碳排放系数,4.035 kgCO2e/kgce;N为一个足够大的正数。
2) 决策变量。

3) 目标函数。
最大完工时间是指从一批订单里的第1个工件的第1道工序加工开始,直至最后一个工件的最后一道工序加工完成所经历的时间。

碳排放量主要是加工设备加工时所产生的碳排放量。为了便于计算,考察国民经济各部门能源消耗及利用情况,常采用标准煤这一标准进行折算,标准煤指的是热值为7 000 kcal/kg的煤炭,碳排放可以引入碳排放系数由标准煤进行计算,根据IPCC的假定,能源的碳排放系数是恒定的[13]。
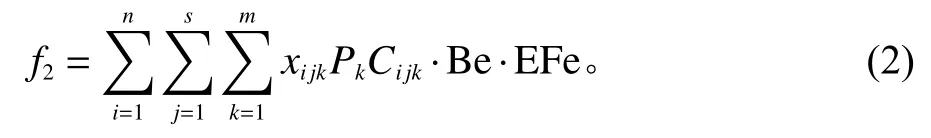
声音的大小一般可以用声压和声压级、声强和声强级、声功率和声功率等级等物理量来描述,通常使用2个物理量的比值——声压级,即分贝(dB)将声音进行量化,描述作为分子的物理量相对于分母这一基准的大小。在铸造车间,噪声主要来源于机器运行产生的噪声、工件加工时工件和机器接触产生的噪声,对于这些结构噪声[14],当机器以一定的功率进行工作时,噪声以平稳的宽频带进行辐射。根据《工业企业厂界环境噪声排放标准》 ,本文采用A级声压对加工噪声的辐射进行评价[15],等效声级可以表示为
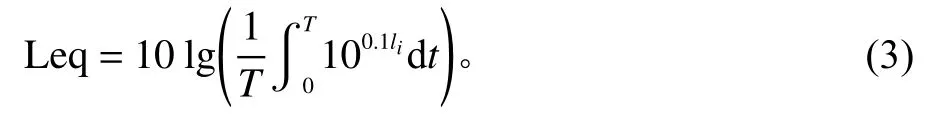
其中,li为t时刻的瞬时A声级;T为测量时间段。当机器以一定功率工作时,可以认为各阶段的辐射声级是确定且不变的。因此,声效等级又可以表示为

其中,li表示时间段i的瞬时A声级;Ti为时间段i。根据本文研究的问题,考虑到由各机器产生的噪声来源不同导致瞬时声压级有所差异,针对各机器运作产生的不同声压级,整个加工过程中所产生的噪声为

式(6)和式(7)表示每个工件的工艺路线不可改变;式(8)和式(9)表示同一时刻一台机器只能加工一道工序;式(10)限制每道工序只能在一台机器上加工;式(11)表明每道工序一旦开始就不允许中断。
2 算法设计
帝国竞争算法(imperial competition algorithm,ICA)是一种受帝国竞争行为启发的智能优化算法[16]。该算法具有较强的全局搜索性能,而且算法利用殖民地向帝国主义国家移动进行局部搜索保证算法具有较强的局部搜索能力,同时帝国竞争操作使帝国内的殖民地向其他帝国移动,突破了原来的搜索范围,提高种群多样性。此外,该算法具有收敛速度快、精度高等优点,近几年被广泛应用到车间调度问题研究中[17-18]。原始的ICA主要通过初始化帝国、殖民地同化及革命和帝国竞争实现种群的迭代寻优。
2.1 编码与解码
针对混合流水车间调度这一离散空间的组合优化问题,本文基于ROV的编码方式生成第1阶段的解决方案。首先,生成矢量数组X={x1,x2,···,xn},x为[−1,1]中的随机数,n为工件的总数,加工工件时依据x的大小从小到大依次进行加工。若有6个待加工工件,则生成一个6维数组X={0.12,−0.78,−0.52,0.17,0.62,−0.19},可以求得该矢量数组对应的加工顺序为2-3-6-1-4-5。这种编码机制极大地缩小解的搜索空间,有利于算法快速寻优,因此广泛应用于流水车间调度问题中。
对于机器选择以及后续阶段的加工顺序通过解码确定。解码是将矢量数组映射为实际问题的解决方案。首先,针对第1阶段的矢量数组,解码可获得工件加工顺序,根据工序的可选加工资源集依次进行资源分配。其次,计算第1阶段加工资源的释放时间,并与工件释放时间相比较,时间差距较小的加工资源具有优先选择权。如果出现多个差距较小的加工资源,则随机选择一个加工资源进行加工。若加工资源从未加工过工件,则认为该加工资源的释放时间为0;否则为上个工件在此加工资源上的加工完成时间。若工件从未被加工过,则工件的释放时间为0。对于后续阶段,将工件的释放时间按升序排序依次进行加工,加工资源延续第1阶段的方式进行排序。
2.2 基于混沌反向学习策略的种群初始化
初始化种群是算法寻优的第1步,其质量和多样性将直接影响算法的性能。本文采用基于混沌反向学习的初始化策略。基于混沌反向学习的初始化策略利用混沌运动随机性及遍历性的特点对当前解进行反向搜索,进而生成多样性高质量的初始种群。具体优化策略如下。
步骤1构建种群规模为N,维度为D的混沌序列Z={Zd,d=1,2,···,D},Zd={Zid,i=1,2,···,N},混沌映射函数为

步骤2通过混沌序列映射到解空间生成初始化种群X={Xi,i=1,2,···,N},Xi={Xid,d=1,2,···,D},Xid可以通过混沌映射函数表达式(13)得到。

其中,Xmax和Xmin分别为个体位置序列随机值的上、下界。
步骤3计算初始种群X的反向种群OX。

步骤4将反向解和初始解进行比较,若反向解优于初始解,则替换初始解形成新的种群X。
2.3 初始化帝国
本文所研究问题为多目标优化,帝国的成本计算更加复杂。为避免计算的复杂度,给出一种简化的帝国初始化机制,具体构建过程如下。
步骤1对大小为N的种群P进行帕累托非支配解排序,得到大小为η的非支配解集π;
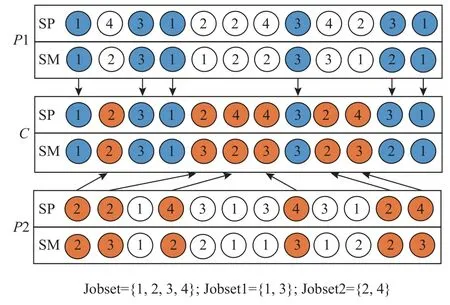
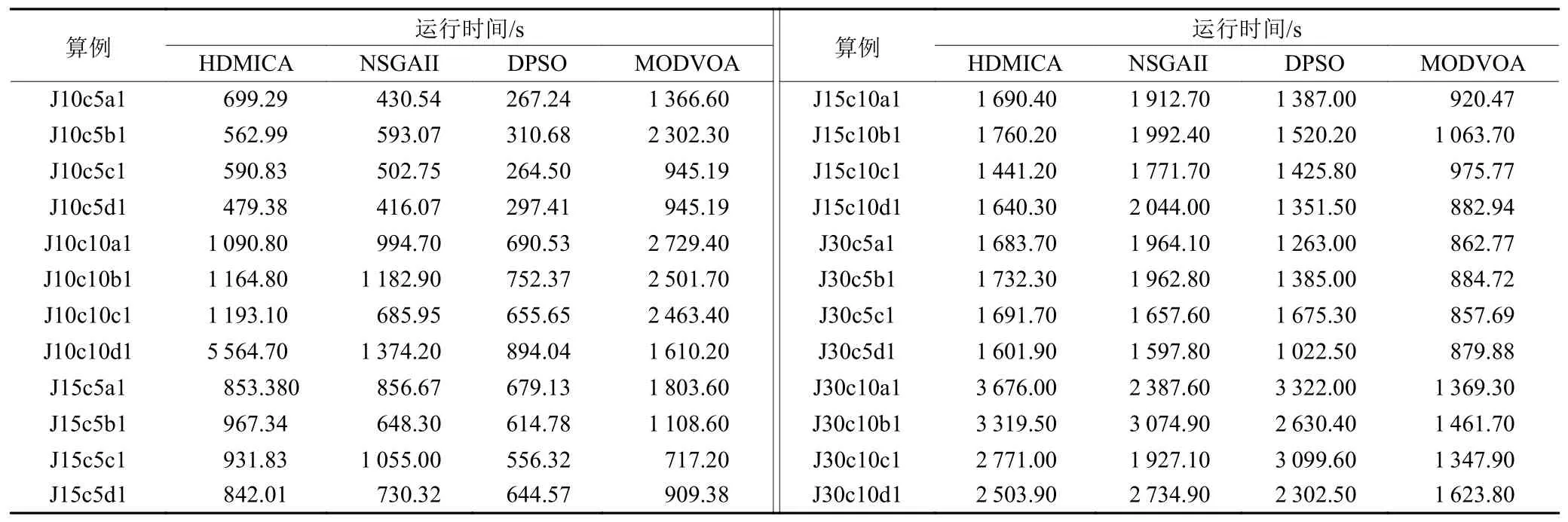
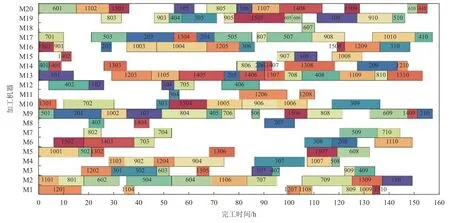
步骤2判断η和帝国主义国家的个数Nemp的大小关系。若η 步骤3随机选择π中的Nemp个个体作为帝国主义国家,由式(15)可计算每个帝国分配的殖民地数,最后一个的殖民地数可由式(16)得出。 步骤4将p中剩余的N−Nemp个个体的层次Rank按升序排序,并交替分配给各帝国。 同化是指使殖民地向帝国主义国家移动,通过殖民地和帝国主义国家不断进行文化交流,实现优异个体带动弱势群体的发展,进而提高帝国的整体成本。通常通过殖民地和帝国主义国家的交叉来实现[19]。本文采用POX交叉来实现殖民地的进化,交叉示意图如图1所示,将工件集Jobset={J1,J2,J3,···,Jn}随机分成两部分:Jobset1和Jobset2,将父代P1中属于Jobset1的工件保持原位置不变复制到子代C中,并把父代P2中属于Jobset2的工件保持顺序不变依次添加到子代C的空闲位置中。 图1 POX交叉示意图Figure 1 Schematic diagram of POX crossover 帝国革命类似于遗传算法(genetic algorithm,GA),为了提高种群的多样性产生某种不可预测的变异,主要对殖民地局部搜索。一般的帝国革命是根据革命率随机选择殖民地进行变异操作。这种做法忽视了殖民地质量的差异性,若质量较差的殖民地发生革命,新个体的质量可能难以达到革命的目的。因此,本文依据Pareto算法对殖民地进行非支配解排序,优先选择第1前沿解集发起革命。设计3种邻域结构对个体进行局部搜索,获取新的个体。3种邻域结构如图2所示。 图2 邻域结构示意图Figure 2 Schematic diagram of neighborhood structure 1) NS1。随机生成两个位置,并反转两个位置间的工序码。 2) NS2。基于关键路径的交换。关键路径是指从操作开始到操作结束的最长加工路线,它决定调度的完成时间。本文采用Nowicki等[20]提出的N5邻域结构,随机选择一个关键路径,并在每个关键块中交换前两个(和后两个)操作来实现。 3) NS3。工序插入操作,从工序码随机选择两道工序a和b,并将工序b插到工序a之前。 帝国主义国家作为精英个体,其相互之间的学习将有更大可能产生优秀个体。针对这一特性,随机选择帝国主义国家进行RPX交叉。可以描述为生成长度为工序总数的向量R,R中的每个元素都是[0,1]中的随机数,并与机器码呈一一对应的关系。首先,将父代P1的工序码复制到子代C中,计算pf值,并将P1中对应的R中元素大于pf的机器码保持顺序及位置不变复制到C中。记录剩余机器码的位置索引,并将父代P2中和工序段对应位置的机器码复制到C中的空缺位置。 其中,It为当前迭代数;Max It为总迭代次数;pfmax和pfmin分别为自适应度值的最大值和最小值。图3为pf=0.6时的交叉示意图。 图3 RPX交叉示意图Figure 3 Schematic diagram of RPX crossover 帝国竞争就是通过计算国家的总质量,势力最弱的国家将被其他国家一步步按一定概率吞并,越是强大的国家概率值越大,吞并殖民地的可能性越大,直至弱势国家的殖民地变为0,该帝国主义国家也被占领,至此整个国家消亡。为实现帝国竞争需要计算国家的总成本,个体i的成本值ci为 其中,Ranki为通过非支配解排序生成的个体i的Rank值;disti为解i的拥挤度距离,由个体i的目标上相邻两个个体的目标值的和组成;表示与目标k相邻的两目标值之间的距离;总的目标数为m;表示Rank值为Ranki的集合,µ为一个接近于0的正数,目的是防止分母为0。 所以帝国k的总成本TCk=ck+ξmean{Cost(colonies of empirek)},其中,ξ为系数,且ξ=0.1。将总成本归一化NTCk=2max{TC}−TCk,最大帝国成本乘以2的目的是防止帝国k的势力为0,将帝国间的势力差距大大减小,使每个帝国都有可能成为竞争中的胜利者,使帝国竞争更加充分。帝国k的势力Epk为 基于以上描述,本文改进的算法流程如图4所示。 图4 算法流程Figure 4 Algorithm flow chart 针对本文研究的混合流水车间调度问题,结合问题模型实际情况设置参数值,并参考Carlier算例[21]设计24个测试算例。其中,工件数n∈{10,15,30},阶段s∈{5,10},每个算例由3个字符和3个整数表示,“J”表示工件,“c”表示加工阶段,第3个字符表示阶段机器布局方式,“a”指中间阶段一台加工机器,其余阶段有3台加工和机器;“b”指第1阶段有一台机器,其他阶段3台机器;“c”是中间阶段有2台加工机器,其他阶段3台机器;“d”指每个阶段都是3台机器。例如,“J10c5a1”表示该问题有10个工件,5个加工阶段,中间阶段一台加工机器的第1种布局,其余阶段有3台加工和机器。各阶段加工资源的加工时间在区间[3,20]上服从均匀分布,各阶段加工资源单位时间能耗在[0.3,3]上均匀产生,各阶段加工资源产生的噪声在区间[70,90]上均匀产生。当阶段数为5时,工序加工机器编号在{1,9}之间选择,第10台机器对应瓶颈工序;当阶段数为10时,工序加工机器编号在{1,19}之间选择,第20台机器对应瓶颈工序。 针对多目标问题采用3种评价标准[22]对非支配解的质量以及多样性进行评价,具体方法如下。 1) 平均理想距离(MID),显示非支配解与理想点(0,0,0)之间的距离。该值越小表示非支配解与理想值越接近,结果越好。 其中,ci=是目标值平方和的平方根;n为非支配解的数量。 2) SNS,是对非支配解多样性地衡量,SNS越大表示非支配解的多样性越丰富,解的质量越好。 3) RAS,同时达到三目标值的概率。 其中,fi=min{f1i,f2i,f3i},RAS越小解的质量越好。 影响HDMICA算法性能的参数主要有国家总数N、帝国主义国家数Nemp、殖民地革命概率的阈值p和迭代次数Max It。经大量实验可确定,当殖民国家数Nemp占国家总数N的10%~20%之间时,算法性能最好。通过正交试验可确定,当种群大小N=100,帝国主义国家数Nemp=10,殖民地革命概率p=0.98,迭代Max It=150次时为算法的最优参数。 为验证所提算法的有效性,选择经典算法NSGAII、DPSO以及MODVOA与之进行对比。为保证各算法结果对比的有效性,所有实验的运行环境均为2.7 GHz CPU,8 G内存,64位Windows 7系统计算机,编程环境为Matlab 2016。为避免结果的随机性,每个算例均独立运行30次,计算目标值的均值以及平均运行时间验证算法的求解质量,计算3种评价指标MID、SNS、RAS的均值验证非支配解的质量。24个算例的对比结果如表1~3所示。 表1 算例仿真结果对比Table 1 Comparison table of simulation results of calculation examples 表1和表2分别给出24个算例仿真结果以及运行时间,从目标值最小化最大完工时间、最小化碳排放以及最小噪声值来看,几乎在所有算例中由HDMICA算法所求结果明显优于其他算法所求结果,且所提算法运行时间同对比算法相差无几,综合分析所提算法具有明显的优越性。由表3可以看出HDMICA虽无法做到所有指标最优,但是相较于其他3种算法从HDMICA的MID以及RAS的大小可以看出,由HDMICA所求得的非支配解能够同时保证3个目标均接近全局最优,最优解最接近全局最优解,算法在收敛性以及解的质量的性能优于其他算法。但是SNS值一般,非支配解的多样性没有明显优势。总体来看,所提算法相较于其他3种算法具有更强的优越性。 表2 算例仿真运行时间Table 2 Simulation running timetable of the calculation examples 表3 算例仿真评价指标对比Table 3 Comparison table of simulation evaluation indicators for calculation examples 以算例“J15c10d1”为例,图5为4种算法所求Pareto第1前沿的目标分布对比图。从图5中可以看出,由HDMICA求得的非支配解分布在靠近坐标最小值的一侧,解的质量明显优于其他算法。 图5 Pareto第1前沿分布图Figure 5 Distribution of Pareto first frontier 图6是从HDMICA所求非支配解中选择的拥挤度距离最大的一个解决方案的甘特图。图中矩形的每种颜色表示一个工件,数字表示加工阶段,例如1003可以描述为工件J10的第3个加工阶段。该解决方案的目标值为加工时间157 h,碳排放量为1 009.90 kgCO2e,噪声为80.03 dB。 图6 算例J15c10d1调度甘特图Figure 6 Example J15c10d1 scheduling Gantt chart 本文以绿色可持续为理论,基于混合流水车间调度问题,建立多目标数学模型,并设计了一种混合离散多目标帝国竞争算法进行求解。最后以24种标准案例证实算法的可行性。在未来的研究中可以对算法求解方面更加优化,寻找更加高质量有效的初始化方法,并同多种经典算法进行对比,而且可以考虑人的行为效应对模型的影响,使模型更加贴近实际生产。对于绿色调度,本文只考虑碳排放以及噪声两个因素,在实际的铸造生产中会产生大量的废渣废气,以后可以在此方向深入研究。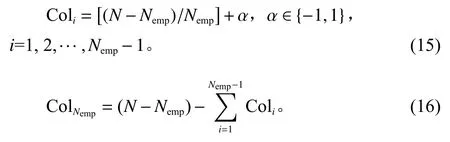
2.4 同化及革命
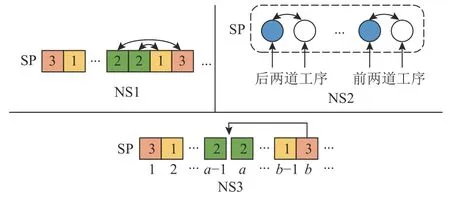

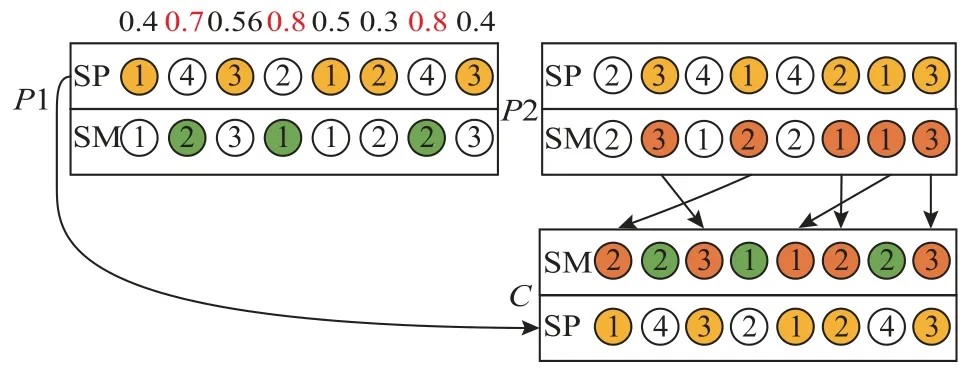
2.5 帝国竞争
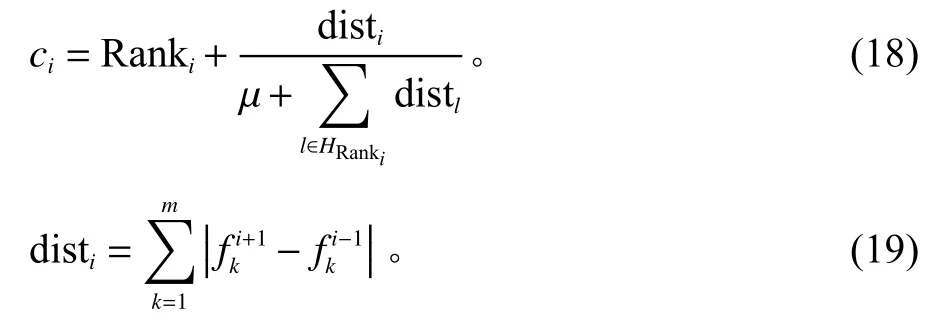


3 仿真结果与分析
3.1 参数确定

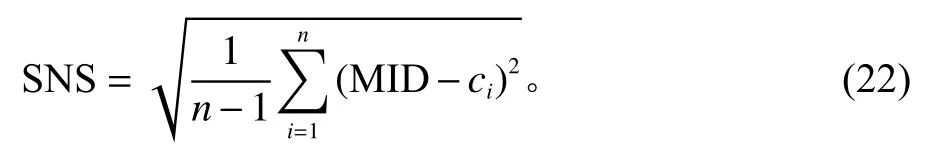

3.2 算法对比



4 结束语
