具有多资源协同约束的作业车间排队网建模与分析
2022-07-15李程平张惠煜陈庆新
李程平,张惠煜,陈庆新,毛 宁
(广东工业大学 广东省计算机集成制造系统重点实验室,广东 广州,510006)
当今制造业正在迈向智能化的新时代,自动化设备如数控机床、工业机器人、自动导航小车(automated guided vehicle,AGV) 等正在逐步取代传统的生产设备并实现生产自动化。然而,受限于人工智能技术的发展水平与制造业应用尚未成熟,目前仍远未达到“自适应、自决策、自执行”的完全智能化阶段。在很多情况下,人力资源仍然是生产过程中不可或缺的生产要素,例如在加工定位精度要求非常高的情况下,需要作业人员预先对机床进行设置并校对工件位置。因此,这类作业车间的生产过程需要由加工(机床)、运输(AGV)、预设(操作工)多类资源进行协同。由于自动化设备、人力资源等生产资源的成本不断上涨,在制造系统中应该如何配置这些制造资源,才能以最低的成本保证预期产能,是规划设计此类制造系统需要解决的重要问题。
定制化生产也是当今制造业的发展趋势。其显著特点就是生产过程具有随机性,例如工件任务到达时间、工艺路径及加工时间、物料运输时间、操作工作业时间等都是不确定的,无法通过传统确定性数学规划模型解决此类生产车间的资源配置优化问题。在各种随机因素的影响下,合理的资源配置结果依赖于精确估算的系统性能指标,因此需要首先建立随机模型描述系统的运行过程,分析系统性能。
仿真法和排队理论建模方法是随机制造系统建模的主要方法[1]。由于该类问题的复杂性,虽然仿真法能够获得更接近生产实际的结果,但是仿真实验需要消耗大量的运行时间[2],而基于排队理论的解析方法只能获得问题的近似解,但耗时很少,这在资源配置优化的迭代过程中可以极大地提高求解效率。本文所研究的作业车间具有3个特征:1)随机不确定性;2)加工机床、运输AGV、预设操作工三者的多重资源协同约束;3)有限容量的缓冲区。上述特征使得针对此类系统模型建立性能分析模型具有很大的复杂性和求解难度。
针对生产系统排队网建模的研究中,文献[3]回顾了重要的排队网络模型的发展以及在制造系统中的应用;文献[4]研究了离散时间服务排队网络的非参数估计;文献[5]建立MX/GY/1/N的排队网模型,并提出该模型的求解方法;Balasubramanian等[6-7]将MX/GY/1/N的排队网模型进一步扩展,应用到非马尔科夫过程中及一般分布中。
在排队网的划分方面,根据缓存区的容量是否有限,可以划分为有限缓冲排队网与无限缓冲排队网。对定制化作业车间而言,在制品数是一个变量且不应过大,因此用有限缓冲的开排队网来描述作业车间。与无限缓冲排队网相比,有限缓冲排队网中缓存区的容量有限,在某些情况下会发生设备堵塞甚至死锁,使得设备的生产效率下降。在多数情况下,有限缓冲的开排队网没有乘积形式的解[8],因此求解有限缓冲的开排队网的难度更加大。求解有限缓冲的开排队网主要有精确法[9]、广义扩展法[10]以及状态空间分解法[8]。对于本文研究的系统,利用精确法求解会导致状态空间维数灾,广义扩展法仅适用于串联、分流和合流结构的系统,而状态空间分解法能有效减少状态空间的数量,并适用于本文所研究的系统。
对具有双重资源约束的随机制造系统的研究中,文献[11]研究了在有限资源的情况下,生产资源在车间加工中心如何分配使得系统在制品数量最少。文献[12]针对具有自动装卸搬运机器人的制造单元,建立排队网模型分析性能指标。文献[13]考虑AGV与制造单元的耦合关系,建立随机路径的AGV排队网模型并对制造系统的生产性能进行分析。文献[14]研究一个基于AGV搬运物料的制造系统,将排队网理论与模拟退火算法相结合,对制造系统的设施布局进行优化。文献[15]针对随机批量搬运物料的制造系统,以系统产能和订单交货期为约束条件建立优化模型,使AGV的投资费用最小。
综上所述,目前针对生产系统的排队网建模的研究中,并未考虑具有多重资源协同约束的情形。因此,本文针对随机环境下,具有“加工机床、运输AGV、预设操作工”多资源协同约束的作业车间,基于Markov过程建立有限缓冲区开排队网模型,并应用状态空间分解法近似求解系统性能指标值,如系统平均产出率、平均在制品和各类资源的利用率等。
1 问题描述
某定制型作业车间的生产布局经抽象化简后建立的排队网模型如图1所示。该生产系统由中心仓库工件达到区域B0、中心仓库工件离开区B1、1辆AGV小车、待加工缓存区Bfi(i=1,2,3)同等并行机床Mi(i=1,2,3)、完工缓存区Brj(j=1,2,3)和1个操作工人组成。未加工的工件随机到达中心仓库B0,等待AGV搬运。机床可以自动装载和卸载工件,但加工前需要操作工对机床进行设置。机床加工完毕后,工件进入机床的完工缓存区Brj。然后,AGV从缓存区Brj搬运工件到中心仓库工件离开区域B1处。已加工工件在B1卸载后,立刻离开系统。
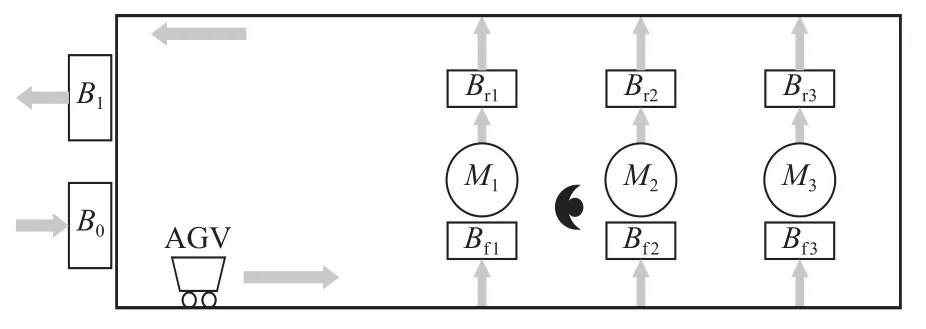
图1 某车间排队网系统模型Figure 1 Queuing network model of a workshop
由此可见,系统生产时受到AGV、机床和操作工人3种资源的约束。若AGV速率较慢,B0会处于常堵塞状态,大量工件会被拒绝进入系统,而机床Mi则会处于饥饿状态;若操作工或机床Mi的速率较慢,B0一样会处于常堵塞状态,且AGV会被缓存区Bfi堵塞。系统模型假设如下。
1) 工件之间相互独立,其到达过程是一个强度为λ 的泊松过程。
2) 当工件到达系统时,进入B0排队等候AGV搬运。若B0的缓存已满,则工件被拒绝进入。
3) 机床M1、M2和M3为同等并行机床,可以自动装卸工件,装卸时间不计。每台机床每次加工一个工件,每次加工时间相互独立,加工时间服从参数为 µ1的指数分布。
4) 机床Mi(i=1,2,3)在加工前需要操作工进行设置,每次的设置时间相互独立,设置时间服从参数为 µ0的指数分布。不考虑操作工移动的时间。
5) 机床发出设置请求后进入等候设置队列,操作工按照先到先服务的规则设置机床。
6) 系统服从后阻塞机制,服务原则为先进先出(FIFO)。
7)B0最大容量为N0,缓存区Bfi(i=1,2,3)最大容量为Nf,缓存区Brj(j=1,2,3)最大容量为Nr。
AGV沿环形路径从B0处搬运工件到缓存区Bfi处卸载,然后到缓存区Brj处把加工完的工件运回B1。现对AGV做出的假设如下。
1) 当AGV到达B0处时,若B0处没有工件,则AGV在B0处等待工件到达。
2) AGV在B0处装载工件后,按照均衡负荷原则选择到工件数量最少的缓存区Bfi卸载工件。
3) 当AGV在缓存区Bfi处卸载工件时,若Bfi已满,则AGV在Bfi处在阻塞等待,直到有空位卸载工件。
4) 若缓存区Brj都没有工件,则AGV在缓存区Bfi卸载完毕后直接返回B0;否则,AGV按照负荷均衡的原则,选择工件数最多的缓存区Brj装载工件,如果两个或以上的缓存区工件数相同,则等概率选择其中一个缓存区装载工件。
5) AGV在两点之间运行的平均时间与两点的路程成正比,且运行时间服从指数分布。
6) 各点之间的距离为dpoint1−point2(见图2),其中,point 1表示起点;point 2表示终点。
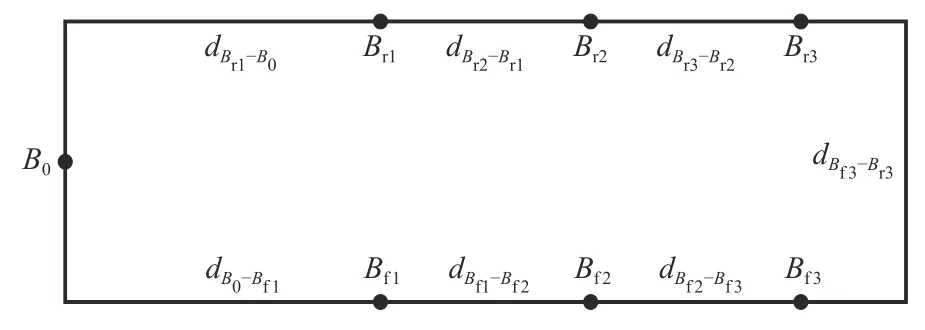
图2 各点之间的距离Figure 2 Distance between points
7) AGV从B0处出发,在途中没有被阻塞的情况下,返回到B0所需的平均时间为1/V。
8) 不考虑死锁。
2 排队网建模及求解
2.1 变量含义
模型中主要变量含义如表1所示。

表1 模型符号及其说明Table 1 Model symbols and descriptions
2.2 系统节点状态分析
由于工件在B1不停留,B1的容量可以看作无穷大,因此不把B1考虑到系统中。将整个制造系统划分为9个节点,各个节点状态转移关系如图3所示。

图3 系统模型分解Figure 3 System model decomposition
2.2.1 AGV节点分析
AGV节点是B0、机床Mi以及缓存区Brj的耦合点,因此将着重对其进行分析。AGV在运输过程中,可能在B0处空闲等待、在Bfi处阻塞等待,根据AGV可能处于的各种不同状态,建立的状态空间及状态空间之间的转移如图4所示。设AGV的状态空间为
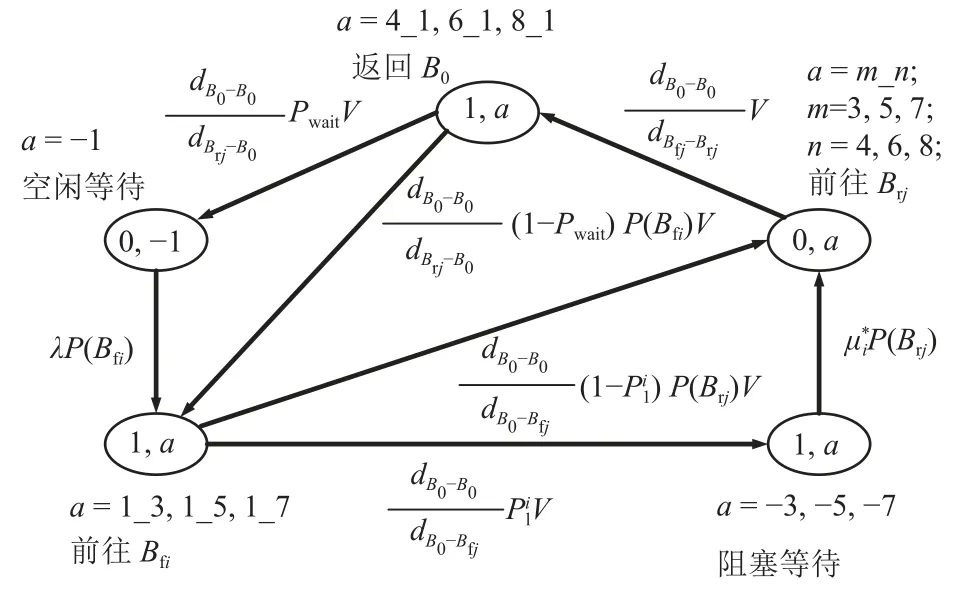
图4 AGV的状态空间转移Figure 4 State space transition of AGV
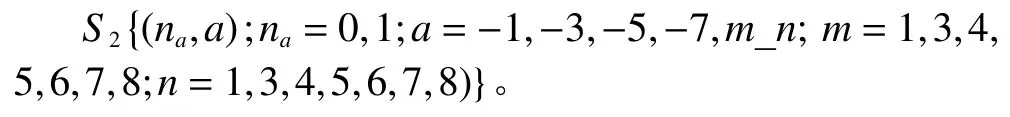
其中,na表示AGV装载的工件数量;a为负数时表示AGV在对应的节点阻塞等待;a=m_n时表示AGV处于从节点m前往节点n的途中。
AGV返回B0时,可能空闲等待,其概率为Pwait。工件以 λ的速率到达B0,则AGV离开状态S2(0,−1)的速率为λ。AGV离开B0后,以概率P(Bfi)选择向缓存区Bfi卸载工件,由于3个机床节点以及缓存区Bfi、Brj是对称的,所以P(Bfi)的值为1/3。AGV到达缓存区Bfi后,可能被堵塞,其概率为。且有
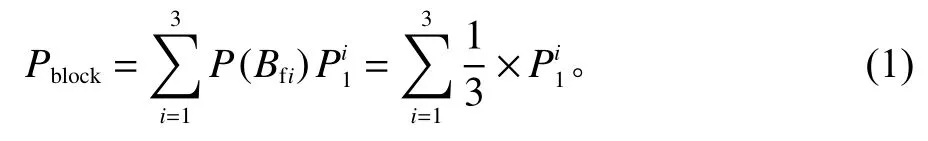
由于按照负荷均衡的原则卸载工件,因此只有当3个缓存区Bfi全满时,AGV才被堵塞。在假设条件中,当缓存区Bfi全满时,AGV将等概率随机选择一个缓存区卸载工件。所以AGV在Bfi被堵塞的概率相等,即。由式(1)可得=Pblock。Pblock的值将根据节点3、节点5及节点7的状态来确定。
若AGV到达缓存区Bfi时被堵塞,则AGV由状态S2{(1,a);a=1_3,1_5,1_7}转移到状态S2{(1,a);a=−3,−5,−7},转移速率为。AGV在Bfi被堵塞后,由于机床加工,Bfi将会产生空位让AGV卸载工件。AGV在Bfi被堵塞的平均时间为机床Mi等待操作工人的平均时间、操作工人设置机床Mi的平均时间与机床Mi加工工件的平均时间之和,AGV解堵速率为被堵塞的平均时间的倒数,同时也为机床Mi不被缓存区Brj(j=i)堵塞时的实际平均加工速率,有

若AGV到达缓存区Bfi时没有被堵塞,则AGV由状态S2{(1,a);a=1_3,1_5,1_7}转移到状态S2{(0,a);a=m_n;m=3,5,7;n=4,6,8},转移速率为×P(Bfi)V。
在每一圈搬运后(AGV从B0处离开再到返回B0处装载工件),设所有机床与缓存区的工件数(Bfi、Mi、Brj一共含有的工件数)为Xn。当n=k时,Xn表示的是从开始时刻到第k圈搬运后所有机床与缓存区的工件数。AGV每次前往缓存区Bfi必定装载着一个工件,可能从Brj装载一个工件或者空车返回B0。所以数列{Xn}满足X1≤X2≤···≤Xn≤Xn+1≤···,且机床与缓存区的容纳量有限,即Xn有界。由于单调有界数列必有极限,当系统处于稳态时,Xn是一个定值,有Xn+1=Xn。
当系统处于稳态时,假若AGV空车返回中心仓库,则 Xn+1>Xn,与Xn+1=Xn矛盾。所以AGV在Bfi卸载工件后空车返回B0的情况只会发生在作业初期,在系统稳态时不会发生。因此有=1,又由对称性可得P(Br1)=P(Br2)=P(Br3)=1/3。
2.2.2 中心仓库B0节点分析
设B0的状态空间为S1{(n0);−1≤n0≤N0},各状态之间的转移如图5所示。当n0≥0时,S1(n0)表示B0有n0个工件,且 AGV小车不在B0处。当n0=−1时,S1(−1)表示B0没有工件,且AGV在B0处空闲等待。则AGV返回中心仓库时,空闲等待的概率Pwait=。

图5 B0的状态空间转移Figure 5 State space transition of B0
B0工件减少,代表AGV从B0离开运行一圈后又返回B0。在这一过程中,AGV可能在缓存区Bfi处被阻塞,被阻塞的概率为。当AGV在缓存区Bfi被阻塞,由式(2)可知,被阻塞的平均时间为。可得AGV平均每一圈的搬运中,被阻塞的时间为

AGV从离开B0到返回B0,平均时间为运行的平均时间与被阻塞的平均时间之和,则

2.2.3 机床节点分析
设机床Mi(i=1,2,3)的状态为{(nfi,u);0≤nfi≤Nf+2;u=w,v;mi=2i+1}。其中,mi代表机床Mi划分的节点;nfi表示机床Mi与缓存区Bfi的工件数量。当nfi=Nf+2时,表示机床Mi与缓存区Bfi的工件数为Nf+1,且AGV被阻塞在缓存区Bfi处。u=w表示机床Mi没有被堵塞的状态,包括空闲等待、等待操作工设置、正在加工工件的状态;u=v表示机床Mi被缓存区Brj(j=i)堵塞。由于不考虑死锁,当AGV被缓存区Bfi阻塞时,机床Mi不会被缓存区Brj(j=i)堵塞,即不考虑这一状态。机床Mi的状态空间如图6所示。

图6 机床Mi的状态空间转移Figure 6 State space transition of Mi
由于AGV按照负荷均衡的原则选择缓存区Bfi卸载工件,因此在状态转移到状态{(nfi+1,u);0≤nfi≤Nfi;u=w,v}的过程中,AGV不会被缓存区Bfi阻塞。则有
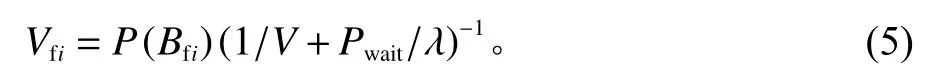
若AGV在缓存区Bfi处被阻塞,可知缓存区Bf1、Bf2、Bf3的工件数量已满,有

机床Mi被堵塞后,解堵的速率为AGV从Brj(j=i)离开后再次到达Brj的平均速率Vrj(其中i=j),则

2.2.4 操作工节点分析
设操作工的状态为S9{(b1,b2,b3);bi=0,1,2,3;i=1,2,3},状态空间如图7所示。bi表示机床在请求设置队列中的位置,当时bi=0,表示机床Mi不需要设置;当bi=k(k=1,2,3)时,表示Mi在设置队列中的第k位。

图7 操作工状态空间转移Figure 7 State space transition of operator
从机床Mi被操作工设置完毕,再到机床Mi需要被设置,共有2种情况。一种情况是机床Mi加工完工件后,缓冲区Bfi还剩余工件要加工;另一种情况是机床Mi空闲,AGV搬运工件到达缓存区Bfi。
机床Mi被设置完毕,Mi的状态为{(nfi,w);1≤n1i≤Nf+2}。在第1种情况下,机床Mi的状态为{(nfi,w);2≤n1i≤Nf+2},则转移速率 φi为
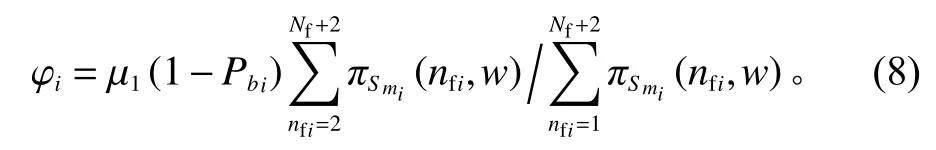
第2种情况下,机床Mi被设置完毕后,机床Mi的状态为。AGV给机床Mi搬运工件的平均时间间隔为1/Vfi,则转移速率 ϕi为

因此,机床Mi从被设置完毕到请求设置的速率为wi=φi+ϕi。
机床M3发出设置请求前,操作工的状态可能有以下几种:S9(0,0,0)、S9(1,0,0)、S9(0,1,0)、S9(1,2,0)、S9(2,1,0)。则机床M3发出设置请求到被操作工设置的平均时间为
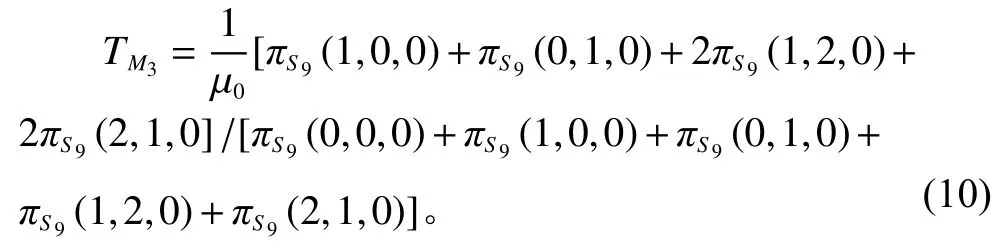
2.2.5 缓存区Brj节点分析
设缓存区Brj的状态空间为{(nrj);0≤nrj≤Nr+1;hj=2j+2},hj代表Brj划分的节点,nrj代表缓存区Brj的工件数量。当nri=Nr+1时表示缓存区Brj有Nr个工件,并且堵塞机床Mi(i=j)。缓存区Brj的状态空间如图8所示。

图8 缓存区Brj的状态空间转移图Figure 8 State space transition of Brj
由于系统达到稳定时,缓存区Brj的输入与输出相等,有

其中,j=i,且有

由式(11)~(13)得
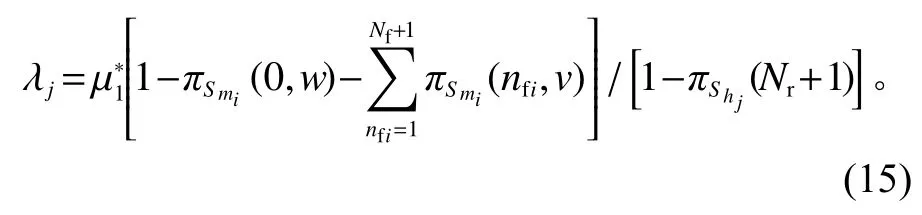
2.3 系统稳态分析
2.3.1 节点状态平衡方程
以中心仓库这一节点为例,状态S1{(n0);0≤n0≤N0−1}的状态平衡方程为

当n0=−1时,有

当n0=N0时,有
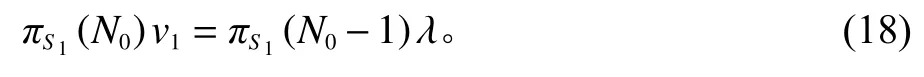
其他各个节点的每个状态的平衡方程都可以照此列出。所有状态平衡方程被列出后,它们组成一个线性方程组。该方程组的系数矩阵是一个稀疏矩阵,且文献[16]证明了连续时间马尔可夫过程的状态平衡方程会在迭代过程中收敛。因此,本文采用迭代法对该方程组进行求解,得出各个状态的稳态概率。
2.3.2 系统生产性能指标
在得出系统节点处于每个状态的概率后,利用某些状态概率可以求出平均生产率与平均在制品数。工件最后是由AGV搬运离开系统的,平均产出率为AGV离开系统的状态概率与离开速率的乘积累加。

平均在制品数量为
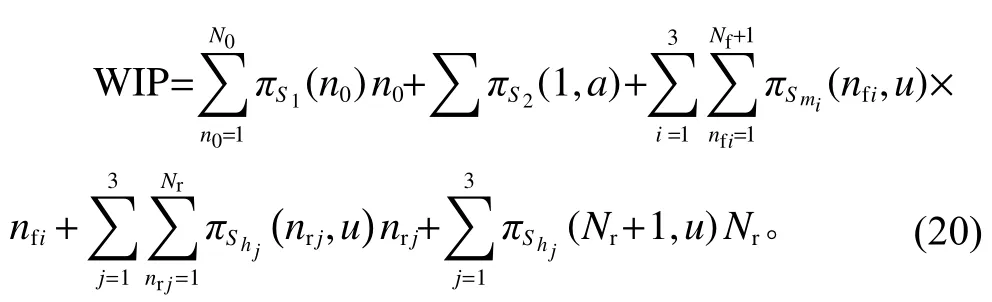
AGV的利用率为

操作工的利用率为

3 算例分析
为了验证状态空间分解法的有效性,利用Tecnomatix Plant Simulation 8.2仿真软件建立对应的仿真模型,并设置一系列算例,将排队网求解的结果与仿真实验得到的结果进行比较。排队网的模型则在Matlab R2014a上进行编程求解。仿真模型的仿真实验和排队网模型的求解计算在同一台PC机上进行,操作系统为Windows 10,硬件环境为Intel(R)CPU 2.30 GHz、16.0 GB RAM。
3.1 离散事件仿真模型
与该作业车间对应的仿真模型如图9所示。为了得到比较准确的结果,仿真的时间要足够长,并且要多次仿真取平均值。在仿真实验中,设置每个算例的仿真时间为100 d,在90 %置信水平下进行20次试验,然后统计生产指标。在该仿真模型中,利用变量的值来代表操作工处于不同的状态,操作工的设置时间通过对应的指数分布随机产生。
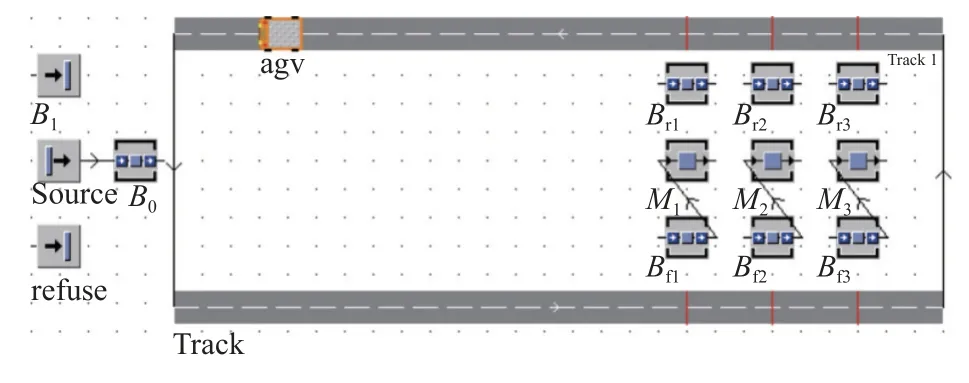
图9 仿真模型Figure 9 Simulation model
3.2 系统性能分析
在算例中,设置4种变化的参数:1)工件到达速率 λ(个/min);2)AGV运输速率V(圈/min);3)操作工设置机床速率 µ0(台/min);4)缓存区的最大容量N0、Nf、Nr(个)。3台机床的加工速率都为µ1=0.4个/min,各点之间的距离如表2所示,算例的参数如表3所示。

表2 各点之间的距离(单位距离)Table 2 Distance between points (Unit distance)
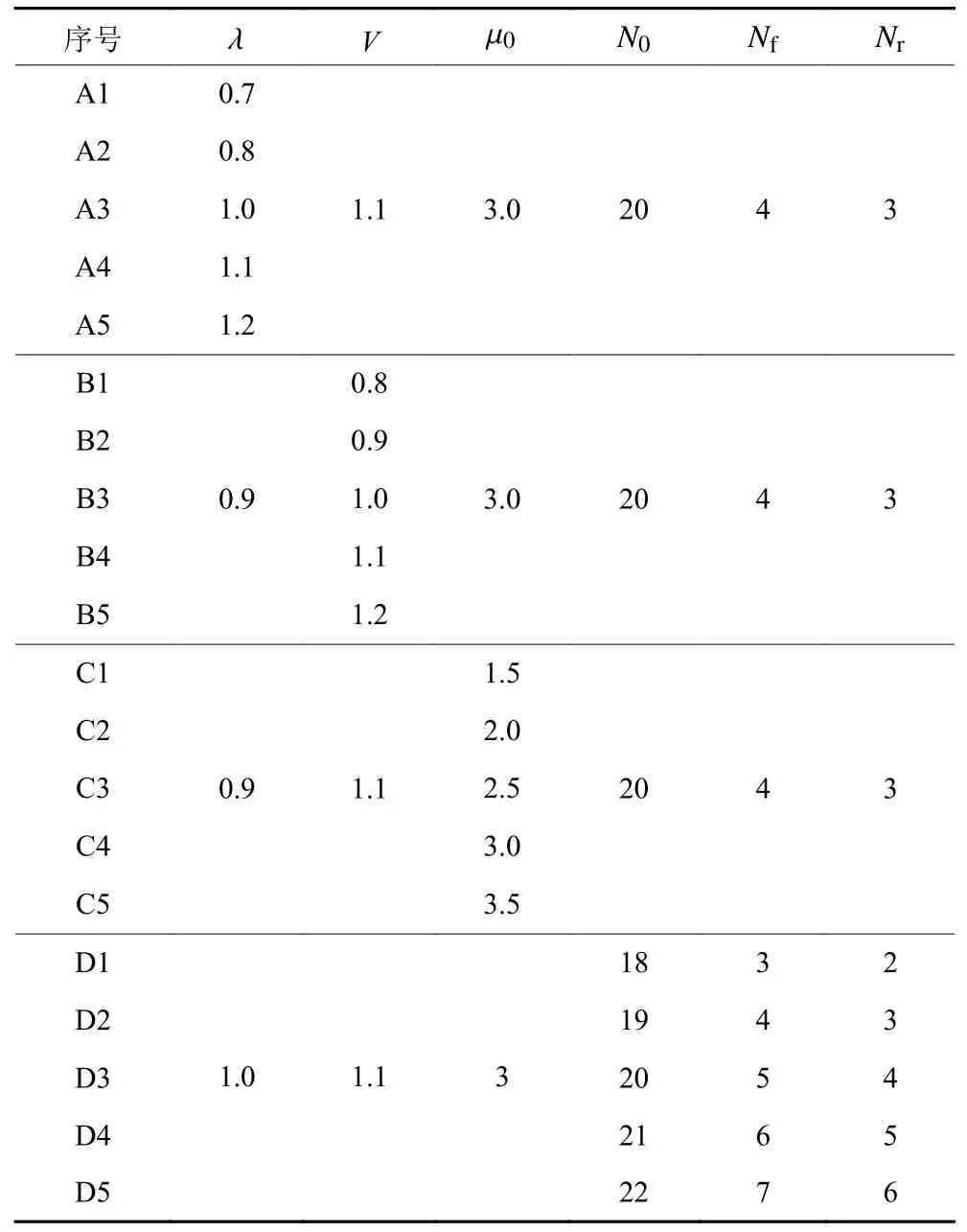
表3 算例参数Table 3 Example parameter
其中,A组探究工件到达速率λ 取不同值时对系统性能的影响;B组探究AGV的运输速率V取不同值时对系统性能的影响;C组探究操作工的设置速率 µ0对系统性能的影响;D组探究缓存区容量对系统性能的影响。实验的结果如表4所示,表中,∆/%表示排队网模型计算值与仿真值的相对误差。各组的平均在制品数、平均产出率、AGV与操作工的利用率的变化规律分别如图10~12所示。从表4的结果可看出,平均在制品的相对误差大部分在5%以内,相对误差最大值为10.99%;平均产出率、AGV利用率和操作工利用率的相对误差都比较小,皆在4%以内,说明本文针对该多资源协同约束作业车间所建立的排队网模型是有效的。

图10 在制品的变化规律Figure 10 The variation of WIP

表4 结果对比Table 4 Comparison of results
由A组的结果可知,当工件的到达速率 λ增大时,系统的平均在制品数、平均产出率、AGV以及操作工的利用率都随之增大。λ不断增大,由于系统处理工件的能力不变,各缓存区的工件数量会有所增大,导致系统的在制品数量增加。系统的产出率先线性增大,然后增大的趋势减小。这是因为当λ比较小时,系统的加工能力足够处理到达的工件,产出率等于工件到达速率;当 λ不断增大,受系统加工能力制约,产出率增大趋势放缓,最终趋于平缓。从图12中A组的结果及式(21)、式(22)可知,当AGV与操作工的速率不变时,其利用率的变化规律与平均产出率是一致的。

图11 产出率的变化规律Figure 11 The variation of throughput
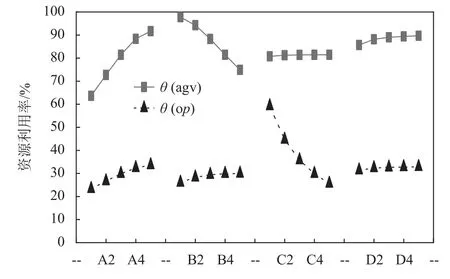
图12 AGV与操作工利用率的变化规律Figure 12 Variation of AGV and operator utilization
由B组的结果可知,当AGV的运输速率V增大时,系统的平均在制品、AGV利用率减小,平均产出率、操作工利用率增加。当V较小时,AGV是系统的瓶颈,AGV速率增大导致系统的加工能力增大,因此产出率随之增大,在制品数量随之减小;V增大到一定程度时,其他资源制约了系统的加工能力,产出率基本不再变化。同时,随着AGV的运输速率V增大,其他因素不变时,AGV的空闲等待时间和AGV被缓存区堵塞的时间增加,导致AGV的利用率下降。
C组的结果的变化规律与B组基本相同,在此不再赘述。
由D组的结果可知,随着缓存区的容量增大,系统的在制品数、平均产出率、AGV利用率和操作工利用率都增大,其中在制品数量增长最明显。由于工件随机到达系统,当缓存区容量较小时,工件被拒绝进入系统的概率会变大,系统在制品、产出率和资源利用率都比较小。缓存区容量增大到一定程度后,产出率接近工件到达速率,基本不再增加,但在制品数量仍在增大,因此缓存区容量必须合理配置。
4 结语
本文针对具有多资源约束的作业车间,考虑系统多资源约束的特点及各节点之间的关系,建立其排队网模型,并利用状态空间分解法求解其性能指标。建立了制造系统的仿真模型,设置一系列案例,将排队网计算的结果与仿真结果进行对比。算例结果表明,在不同参数的情况下,具有多重资源约束作业车间的有限缓冲开排队网模型是有效的,系统性能计算的相对误差大都在5%以下,验证了状态空间分解法的有效性与精确性。在求解出作业车间的生产性能指标后,通过改变工件到达速率、AGV运输速率等参数,探究不同的资源配置对系统性能的影响,可为进一步研究多重资源协同约束的随机制造系统的资源配置优化提供参考。
未来将在本文的基础上,考虑更大规模定制型作业车间,在保证预期产能的情况下,研究作业车间的资源配置优化问题。
