某大跨度拱桥的台风抖振响应分析
2022-07-15张建国温祖坚姚俊颖张建霖
张建国,温祖坚,姚俊颖,张建霖
(厦门大学建筑与土木工程学院,福建 厦门 361005)
近几十年来,我国东南沿海地区的经济迅速发展,与之相呼应的大型交通基础设施也不断涌现,其中就包括了大量的跨海公路桥梁.拱桥因形态优美、施工方便,在较多的城市道路和沿海快速通道中得到了运用.但我国东南沿海地区在夏秋两季经常会受到强台风的侵袭,易造成桥梁和建筑的风致破坏.因此,大跨度的拱桥结构在台风作用下的风致响应和安全性评估是一个值得研究的课题.
在实际桥梁的抖振计算方面:Li等[1]进行了青马大桥在台风“约克”(York)过境时的疲劳损伤全过程计算,认为风致桥梁结构抖振造成的疲劳破坏要比正常交通情况大得多;程进等[2]在计算得到拱桥三分析系数的基础上,分析了上海卢浦大桥在静风荷载作用下的响应;王贤亮等[3]制作了缩尺比为1∶100的朝天门大桥气动弹性模型,根据风洞实验结果得到了成桥状态下的抖振响应;胡旭辉等[4]分析了某斜拉桥施工最大单臂阶段的抖振响应,表明20 m/s风速下悬臂结构的竖向加速度将超过限值;沈正峰等[5]针对某悬索桥的双主梁进行了频域和时域抖振计算,提出了在抖振计算时应考虑气动力的展向变化.
在大跨度拱桥风致抖振响应的理论研究方面:Davenport[6]基于准定常理论建立了抖振计算模型;Scanlan[7]考虑气动耦合现象,基于颤振理论提出了桥梁抖振的修正计算模型;苏益等[8]提出了一种大跨度桥梁抖振响应计算的直接估算方法.
上述研究并未针对台风作用下大跨度拱桥的抖振响应进行专门的分析,计算时所用的风速时程是根据Davenport风速谱等谱函数,由谐波合成等方法模拟求得,而桥梁各构件的三分力系数一般是根据风洞试验数据获取.全桥气弹模型实验可直观获得桥梁的抖振响应全过程,但耗费大、时间长.本文拟以一座真实的大跨度拱桥为例,运用计算流体力学(computational fluid dynamics,CFD)求得桥梁各构件的三分力系数,以台风“苏迪罗”的某一稳定时段的实测风速时程作为荷载输入,根据Davenport抖振计算模型进行时程分析,求得桥梁在台风作用下的抖振响应.本文所述方法采用的风速时程来源于实测数据且可替代风洞试验求得较为合理的桥梁抖振响应结果,可供沿海桥梁的台风风致疲劳及破坏分析参考借鉴.
1 台风“苏迪罗”风场特性
为获取台风的风速风向时程数据,在厦门大嶝岛靠海位置建造了4座台风实测塔,沿直线布置.将4座测风塔依次命名为P1、P2、P3和P4,其高度分别为20、40、40和20 m.相邻两塔之间的间距依次为30、90和60 m.测风塔P1和P4分别安装2个风速仪,P2和P3分别安装4个风速仪,共12个风速仪,各塔上风速仪沿高度的间距均为10 m.测风塔和风速仪的布置如图1所示.

图1 测风塔及风速仪布置图Fig.1 Layout of the wind towers and anemometers
台风“苏迪罗”于2015年8月8日凌晨登陆中国台湾花莲市,登陆时中心附近最大风速为48 m/s,风力为15级.台风离开台湾岛进入台湾海峡后,于当日22:00在福建莆田市第二次登陆.本文所述的四座测风塔成功地测得了台风“苏迪罗”影响厦门大嶝岛的风速全部数据.图2给出了P2塔在15:50—16:00时段的顺风向风速和风向时程,可以看出,在这10 min时段内,10 m和40 m高度处的风速风向时程均在一个常数附近上下较为规则地波动,可看作平稳随机过程,其余11个风速仪所测数据与此类似,这里不再赘述.
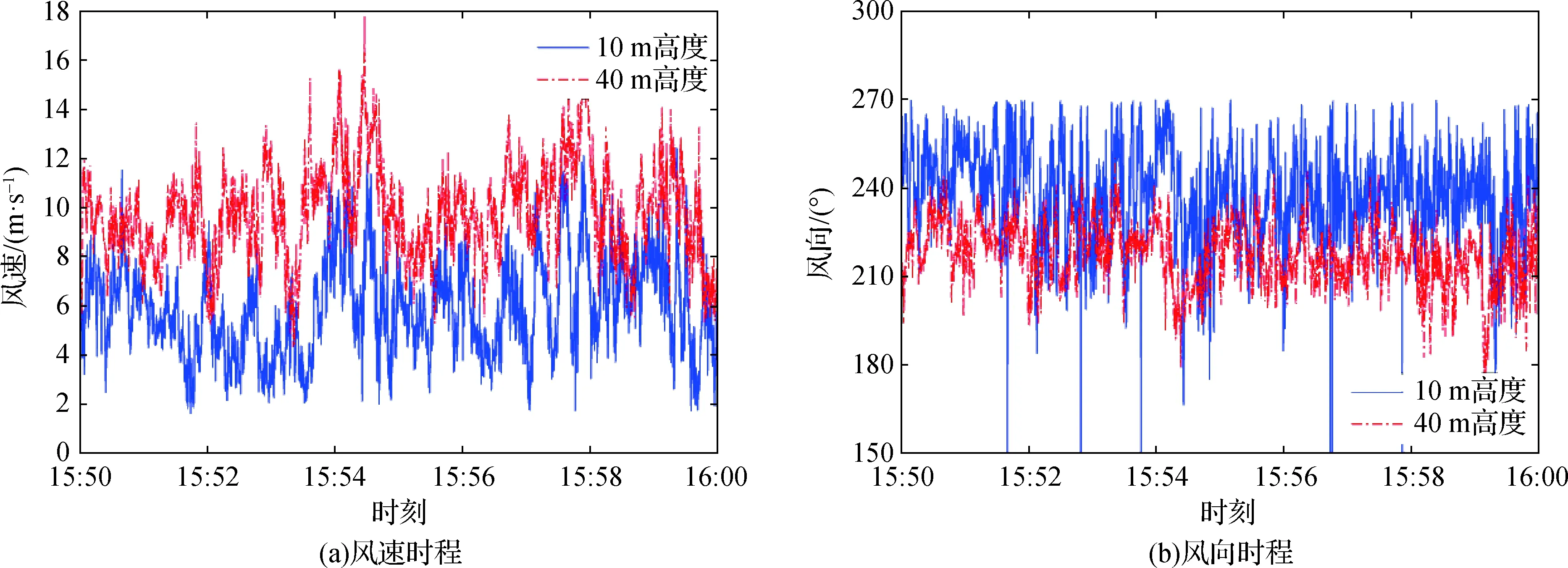
图2 P2塔测得台风“苏迪罗”的风速和风向时程Fig.2 Wind velocity and wind direction time history of typhoon “Soudelor” test by P2 tower
基于准定常理论的桥梁抖振计算方法主要与台风顺风向和竖直方向的脉动风速特性有关,式(1)和(2)分别给出了顺风向和竖直方向Von-Karman谱的表达形式,P3塔30 m高度处实测风速谱与Von-Karman谱的对比情况如图3所示,其他风速仪所测数据与此类似,此处不再赘述.

图3 近地台风功率谱密度函数Fig.3 The power spectral density function of near-ground typhoon
(1)
(2)
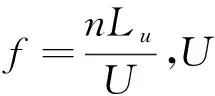
可以看出,台风“苏迪罗”顺风向和竖直方向的脉动功率谱密度函数与Von-Karman谱吻合良好,这与王旭等[9]、李波等[10]学者的结论是一致的.
如引言所述,大量学者的研究方法均是利用Davenport风速谱公式,采用谐波合成等时程模拟方法,首先得到脉动的风速时程数据,进而进行近海桥梁在台风作用下的风致抖振响应.由于台风风速谱通常并不符合Davenport谱的形式,如此处理可能造成不安全的结果.根据本小节分析结论,研究者可基于Von-Karman谱进行风速时程模拟,或直接运用现场实测风速时程,由此计算近海桥梁在台风下的抖振响应.
2 某大跨度拱桥的气动力特性
2.1 桥梁抖振力计算公式
本文拟采用文献[6]所述的抖振力计算模型确定作用于大跨度拱桥各构件上的抖振力,其计算公式如式(3)和(4)所示.
(3)
L(t)=
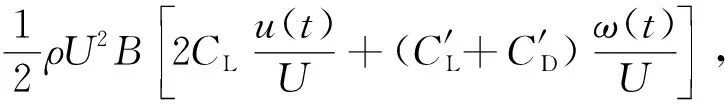
(4)
式中,D(t)、L(t)分别为桥梁水平构件的阻力和升力,ρ为空气密度,U为来流平均风速,D和B分别为桥面的高度和宽度,u(t)、ω(t)分别为顺风向和竖直方向的脉动风速,CD、CL、C′D、C′L分别为阻力系数、升力系数及其各自的导数.
可以看出,当桥梁几何参数D和B以及来流脉动风速u(t)和ω(t)确定后,计算桥梁抖振力的关键是需要确定CD、CL、C′D、C′L这四个参数.2.2节将介绍运用CFD求得桥梁各构件的阻力/升力系数.
2.2 桥面与拱肋的CFD建模及阻力/升力系数计算
本文所述的大跨度拱桥桥面由钢箱梁与梁上混凝土预制板整体现浇而成,钢箱梁平均高度2.28 m,桥面宽34 m,其上布置250 mm厚度的混凝土桥面板,其下封闭.主跨拱的拱肋截面为矩形加劲梁,截面宽度为2.56 m不变,但截面高度随着位置产生渐进变化,拱脚处的截面高度为4.5 m,拱顶处的截面高度为2.5 m,主跨拱的主轴线为二次抛物线.
采用Fluent软件分别计算桥面断面和拱肋断面的阻力/升力系数,由于拱肋断面尺寸连续变化,为简便起见,本文沿拱轴进行了4个断面的阻力/升力系数计算.计算区域均取为30B×20D,采用结构化网格,计算域内采用四边形网格进行离散,靠近主梁断面处使用边界层网格进行离散,保证y+值在[30,100],模型及网格划分如图4所示.

图4 Fluent中的桥面和拱肋断面模型及网格Fig.4 Model and grid of deck and arch in Fluent
采用SIMPLE算法进行流体动力学模拟计算,选择标准k-ε湍流模型.进行CFD计算时,采用的边界条件如下:
1) 入口边界条件:采用速度边界条件,风速设定为12 m/s;
2) 出口边界条件:采用压力边界条件,设定相对压力为0;
3) 内部边界条件:采用壁面边界.
针对桥面和拱肋各位置的断面均进行了风攻角α∈[-3°,3°]的计算,得到的阻力/升力系数如表1所示,为简便起见,表中仅给出了跨中拱肋处的系数数值,其余断面的数值略有不同,但变化规律一样.

表1 桥面和拱肋的阻力/升力系数
由表1可以看出,桥面和拱肋的阻力系数在0°风攻角时最大,随着风攻角绝对值越大,其值越小,原因是这两种构件的断面基本是上下对称的.桥面和拱肋的升力系数随风向角的变化规律则正好相反,风向角的绝对值越大,升力系数的绝对值也越大,负号代表与坐标轴的正向相反.
根据表1中的CD和CL值,采用差分方法可直接得到阻力/升力系数的导数C′D、C′L的数值,代入式(3)和(4)即可求得作用在各构件断面上的抖振力.
3 某大跨度拱桥的风致抖振响应
3.1 桥梁整体建模
某大跨度拱桥位于厦门岛东北部的内湖与台湾海峡海洋交界处,距离本文所述的4座测风塔的距离仅为15.3 km,周边同样为宽阔地带,两地之间也是宽阔海域.大跨度拱桥的总长度为324 m,为三跨中承式提篮式拱桥,其中中跨的长度为208 m,两边跨的长度均为58 m,主桥宽度为34 m.
根据施工图纸,本文建立了该桥的ANSYS有限元模型如图5所示.建模时,桥面主梁和拱肋采用梁单元Beam189模拟,吊杆采用杆单元Link8模拟,材料均为线弹性钢材,弹性模量为210 GPa.吊杆与拱肋的连接为铰接,其余连接均为刚接.

图5 大跨度拱桥有限元ANSYS模型Fig.5 Funite element model of long-span arch bridge in ANSYS
为了验证模型的正确性,本文进行了桥梁的自振特性分析,得到的前三阶自振频率如表2所示.可以看出,该大跨度拱桥的自振频率符合一般拱桥的自振特性规律,桥梁的一阶频率较低,属于风荷载敏感的工程结构.

表2 大跨度拱桥的自振频率
3.2 风荷载施加
如前所述,本文所述拱桥与测风基地的直线距离很近,两者之间为宽阔海域,没有明显山体和建筑物遮挡,本文认为在同一次台风时,桥址处的风场特性与台风观测点处的风场特性基本相同.
4座测风塔的最大水平间距为180 m,与桥梁主跨208 m的长度接近,可将所测的某一个10 min风速样本作为荷载直接作用在主跨上.为计算方便,主跨上间隔15 m设定一个荷载施加点,合计15个;边跨上间隔20 m设定一个荷载施加点,合计4个.假设拱肋仅在高出桥面部分承受风荷载,按水平投影距离15 m 设定一个荷载施加点,合计20个.图6为所有风荷载施加点的示意图.

图6 风荷载施加节点Fig.6 Nodes of wind loads
根据荷载施加点高度的不同,分别取测风塔不同高度处的风速计算作用在荷载施加点上的风荷载,桥面高度为22 m,因此主梁上承受的风速可取20 m高度处的10 min台风风速样本;根据主梁荷载施加点水平距离的不同,编号1~3、37~38号施加点可取P1塔的20 m高度处数据,编号4~7号施加点可取P2塔20 m高度处数据,编号8~12号施加点可取P3塔的20 m高度处数据,编号13~15、39~40号施加点可取P4塔20 m高度处数据.除了20 m高度处的数据外,拱肋上的荷载施加点风速数据沿高度变化,施加点高度在25~35 m 之间的,可取30 m高度处的数据,高度在35 m以上的施加点,可取40 m高度处的风速数据.
根据式(3)和(4),代入阻力/升力系数和实测风速时程,可给出台风“苏迪罗”过境时,不同风攻角下桥面和拱肋各节点上受到的抖振力时程.篇幅所限,本文仅给出15:50—16:00时段、0°风攻角时,跨中桥面每单位长度上所受到的阻力和升力时程,如图7所示.

图7 跨中桥面单位长度上的风荷载Fig.7 Wind loads on the middle deck per unit length
3.3 大跨度拱桥抖振分析结果
将图7所示的抖振力加上静风力,可得到作用在结构上的总体风荷载,将其分别施加到荷载施加点上进行时程分析,计算时间步长按照风速采样周期取为0.1 s,利用ANSYS的瞬态分析功能计算各时间段大跨度拱桥的位移响应,积分方法选为Newmark-β法.由于风荷载为平稳随机荷载,考虑到计算效率,本文风荷载作用的时长并未选取10 min,仅选取前50 s进行了时程分析计算,这样所得结果的统计特性与10 min的统计特性是一致的.
0°风攻角时,桥面跨中和1/4跨度处的抖振响应时程如图8所示.表3则给出了桥面跨中和1/4跨度处在3个风攻角下的抖振位移响应最大值和均方根值.
由图8和表3可以看出,桥面跨中和1/4跨度处的竖向位移远大于横向位移,这是因为桥梁的横向刚度要远大于竖向刚度,同时竖向的风荷载也大于横向风荷载的缘故.跨中处的竖向位移要大于1/4跨度处的竖向位移,跨中和1/4跨处的水平位移均很小,差别不大.

图8 跨中和1/4跨度处的位移响应Fig.8 Displacement response of middle and 1/4 span
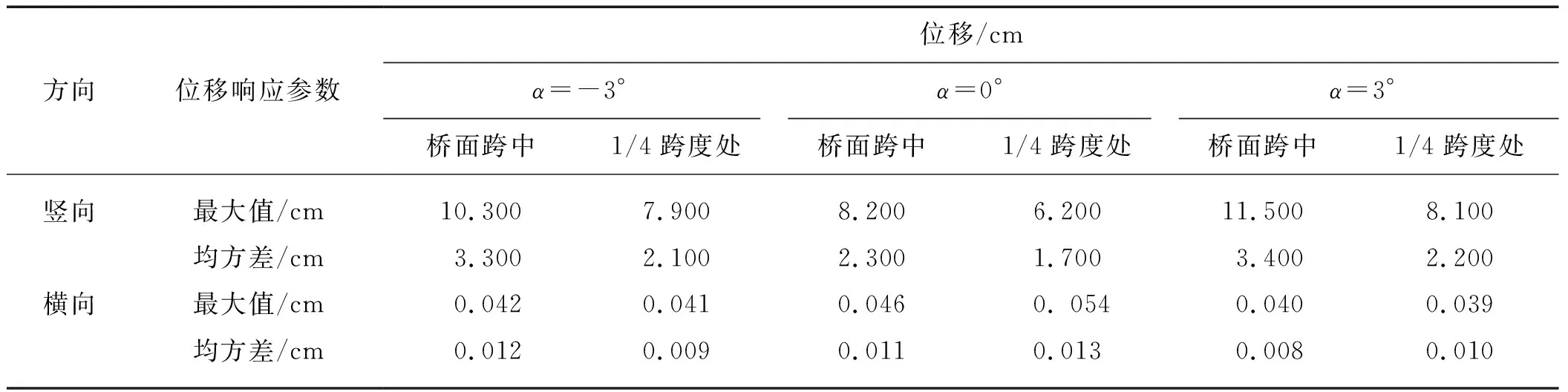
表3 位移的最大值和均方差
从具体数值来看,由于“苏迪罗”台风的风速不大,在此作用下,桥面跨中最大位移与桥梁总跨度的比值仅为0.000 4,说明在类似强度的台风作用时,桥梁的安全性是可以保证的.
4 结 论
本文基于Davenport准定常桥梁抖振力模型和CFD计算得到的三分力系数,给出了“苏迪罗”台风过境时,作用在沿海某大跨度拱桥上的抖振力,通过ANSYS瞬态时程分析,得到了桥梁的台风风致响应时程,验证了桥梁在台风作用下的安全性,得到的结论如下:
1) 台风脉动风速的功率谱密度函数与常态风存在明显差异,其风速谱与Von-Karman谱较为吻合;
2) 运用CFD数值风洞方法可较快速地得到桥梁各构件的三分力系数,是替代风洞试验的一种可行方案;
3) 在沿海地区,可将测风塔实测的风速时程用于计算工程结构的台风风致响应,所得结果具有实际的工程意义.
