干湿循环下花岗岩残积土裂隙演化及边坡稳定性

2022-07-15杨雪菲陈东霞

厦门大学学报（自然科学版） 2022年4期

杨雪菲，陈东霞,2*，刘越

(1.厦门大学建筑与土木工程学院，福建厦门 361005；2.厦门市交通基础设施智能管养工程技术研究中心,福建厦门 361005)

花岗岩残积土在我国福建、广东、香港等南方地区广有分布.这些地区属亚热带海洋性季风气候，干湿季节交替明显[1].自然状态下残积土反复经历干燥、湿润的循环，导致残积土内部胶结物质流失，影响残积土的力学性质[2].以往的研究表明，残积土在干湿循环作用下，土的内摩擦角基本不变，但黏聚力下降明显.这主要是由胶结物质流失导致[3].胶结物质流失使得土颗粒之间的黏结变得脆弱，在之后的干燥过程中易产生裂隙[4].裂隙削弱了土体强度，增加了土体渗透性，破坏了土体结构的完整性.台风暴雨天时雨水沿裂隙入渗加快，边坡内部基质吸力降低，边坡在张拉裂隙处易产生应力集中，进一步加速裂隙发展，降低边坡稳定性[5].因此，研究干湿循环作用下花岗岩残积土的裂隙演化规律及其对强度的影响，可为考虑裂隙影响下的残积土边坡稳定性分析提供理论基础.

通过计算机图像处理技术可以获取裂隙的节点、条数、宽度、长度及面积等参数，这些参数是反映裂隙扩展规律的重要指标.不少学者对干湿循环作用下土体裂隙的演化展开研究.胡东旭等[6]对干湿循环下裂隙体积变化采用Logistic函数预测裂隙在试样局部的发展及分布情况.王建立等[7]开展自然蒸发条件下的土体裂隙试验，采用IPP(integrated performance primitives)图像处理技术提取数据并建立了裂隙扩展长度与含水率的Boltzmann生长曲线模型.裂隙扩展往往伴随土体强度降低.陈开圣[8]研究了干湿循环作用下的红黏土裂隙演化规律，得到了红黏土在干湿循环作用下抗剪强度指标与裂隙密度呈二次多项式的关系.汪时机等[9]对干湿循环效应下膨胀土裂隙演化和土的结构强度展开试验研究，发现裂隙扩展分为酝酿期、传播期和平稳期3个阶段，裂隙扩展致使膨胀土黏聚力大幅降低，其中裂隙面积率与黏聚力衰减相关度最大.刘俊东等[10]监测了黏性土干缩裂隙网络在干湿循环中的变化.杨济铭等[11]利用数字图像相关技术对干湿交替作用下膨胀土边坡裂隙进行监测，监测结果表明脱湿开裂过程中边坡表面裂缝发育形成裂隙网格，裂隙网格为水分提供入渗通道，进而导致裂隙沿深度发展贯通，降低膨胀土边坡稳定性.周立阳等[12]对干湿循环下裂隙性黄土开展单轴压缩试验，分析黄土的裂隙率、分形维数与干湿循环次数之间的关系，得出单轴抗压强度随干湿循环次数增大呈减速衰减特征.

当某个部位土的拉应力大于土体的抗拉强度时，裂隙尖端开始产生.关于裂隙扩展理论的研究，Lu等[13]发现非饱和土抗拉强度主要由土的黏聚力决定，而干湿循环作用会降低土的黏聚力，进而降低土体抗拉强度，导致裂隙产生并扩展.Shi等[14]通过分析干湿循环作用下非饱和膨胀土抗剪强度降低引起土体抗拉强度下降和裂隙扩展的变化规律，量化裂隙扩展和干湿循环的关系，推导了干湿循环作用次数，土体含水率为主要参数的裂隙深度计算公式.随后，Shi等[15]又从损伤角度推导了裂隙深度计算公式，进而从理论上完善了干湿循环作用下膨胀土的裂隙扩展规律.Thi等[16]利用有限元程序，将裂隙作为黏弹性损伤单元，对干燥过程中黏性土体的裂纹扩展展开数值模拟，进一步验证了裂隙扩展与土体物理力学性质的密切联系.刘越等[17]开展了干湿循环下残积土边坡模型试验，分析了裂隙深度与残积土强度衰减之间的量化关系.

综上可知，土体裂隙演化伴随抗剪强度的降低，而强度降低又进一步加速裂隙的扩展.以往的研究主要以膨胀土、黄土或黏性土为研究对象.花岗岩残积土因形成条件及矿物成分，其工程特性有别于膨胀土、黄土和黏性土.因此，本文利用边坡模型试验定量分析干湿循环作用下花岗岩残积土的裂隙扩展规律及其对抗剪强度的影响，进而分析裂隙影响下残积土边坡的稳定性.

1 边坡模型试验

建立花岗岩残积土边坡模型，在边坡的设计深度取环刀试样进行直剪试验，测量边坡土体的抗剪强度.同时拍摄观察边坡裂隙与变形，记录边坡表面的裂隙扩展情况，量化干湿循环下边坡模型的裂隙发育，得出不同干湿循环幅度及干湿循环次数下残积土边坡的裂隙响应.

试验采用厦门市某学生公寓附近花岗岩残积土，砌筑坡脚30°边坡展开模型试验.边坡的坡顶宽0.37 m，坡顶处高0.95 m，坡脚宽0.50 m，坡脚处高0.30 m，整个坡长2.00 m.将一个模型箱分成两个相同的隔间，分层填筑边坡，并在8 cm深度处安装水分传感器.实际的边坡模型如图1所示.

图1 花岗岩残积土边坡模型Fig.1 Slope model of granite residual soil

对模型试验采用的残积土进行物理性质试验，测得土的物理性质指标：土粒相对密度为2.72，干密度为1.78 g/cm3，饱和含水率为24.2%，塑限为20%，液限为47%，塑性指数为27.残积土的颗粒级配比如表1所示.

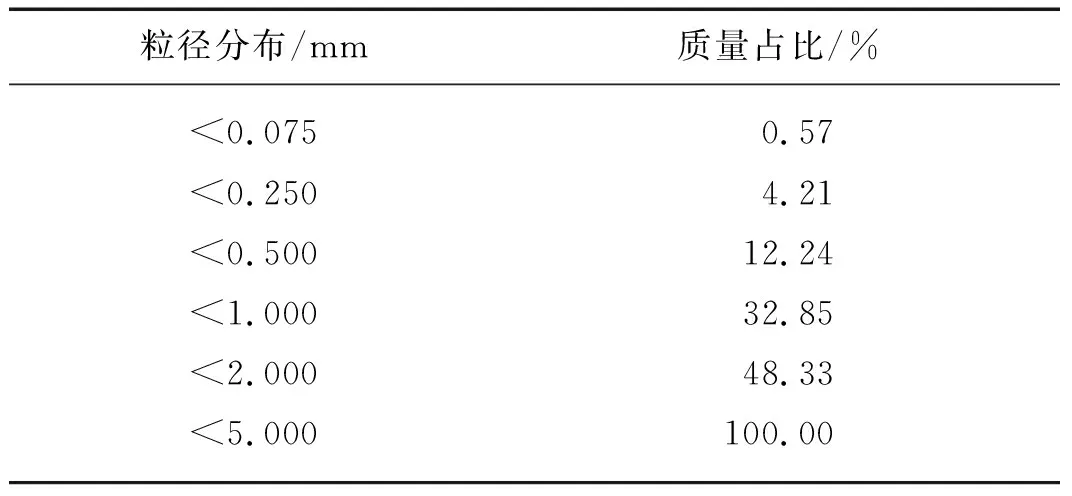
表1 花岗岩残积土粒径分布

模型试验加湿和干燥装置如图2所示.加湿过程由8个喷头喷淋加湿，干燥过程由6个大功率灯泡及4个花篮式取暖器进行干燥.左、右两个边坡分别设置为12.5%～24.0%的大干湿循环幅度和17.5%～24.0%的小干湿循环幅度，进行5次干湿循环.当8 cm深度处的水分传感器显示达到设计含水率时，停止湿润或干燥过程.设计边坡土样的直剪试验取样如图3所示.

图2 干燥和加湿装置Fig.2 Drying and humidifying device

图3 直剪试样环刀取样Fig.3 Direct shear soil sampler

每次干湿循环结束后，在坡顶固定位置拍摄裂隙扩展情况.分析在干湿循环过程中边坡土的强度，裂隙扩展与干湿循环的关系，讨论不同干湿循环幅度对试验结果产生的影响，得到干湿循环次数、干湿循环幅度、裂隙扩展情况和土体强度参数之间的关系.

2 模型试验结果分析

2.1 干湿循环对边坡裂隙发育影响

每次干燥过程结束后，拍摄边坡模型表面照片，记录顶部裂隙的发育情况.在边坡干燥过程中，土体含水率逐渐降低，边坡表面的土体失水收缩产生裂隙.5次大干湿循环幅度(BDW)作用下，边坡模型顶部表面的裂隙如图4所示.

图4 大干湿循环幅度(12.5%～24.0%)边坡顶部裂隙的扩展Fig.4 The crack propagation on the top of slope under large amplitude dry-wet cycle (12.5%～24.0%)

通过对裂隙图像的二值化和矢量化处理可得到裂隙的长度、面积、分布密度等几何要素，以大循环幅度下第5次干湿循环后的坡面裂隙为例，处理结果如图5所示.

图5 裂隙图像的二值化和矢量化Fig.5 Binarization and vectorization of crack image

采用裂隙的面积率来定义裂隙度：

(1)

式中，δf为裂隙度(%)，A为照片中土体面积，Ai为第i条裂隙所占面积.n表示裂隙数量.干湿循环试验中统计计算的裂隙度列于表2，裂隙度与干湿循环次数的关系如图6所示.

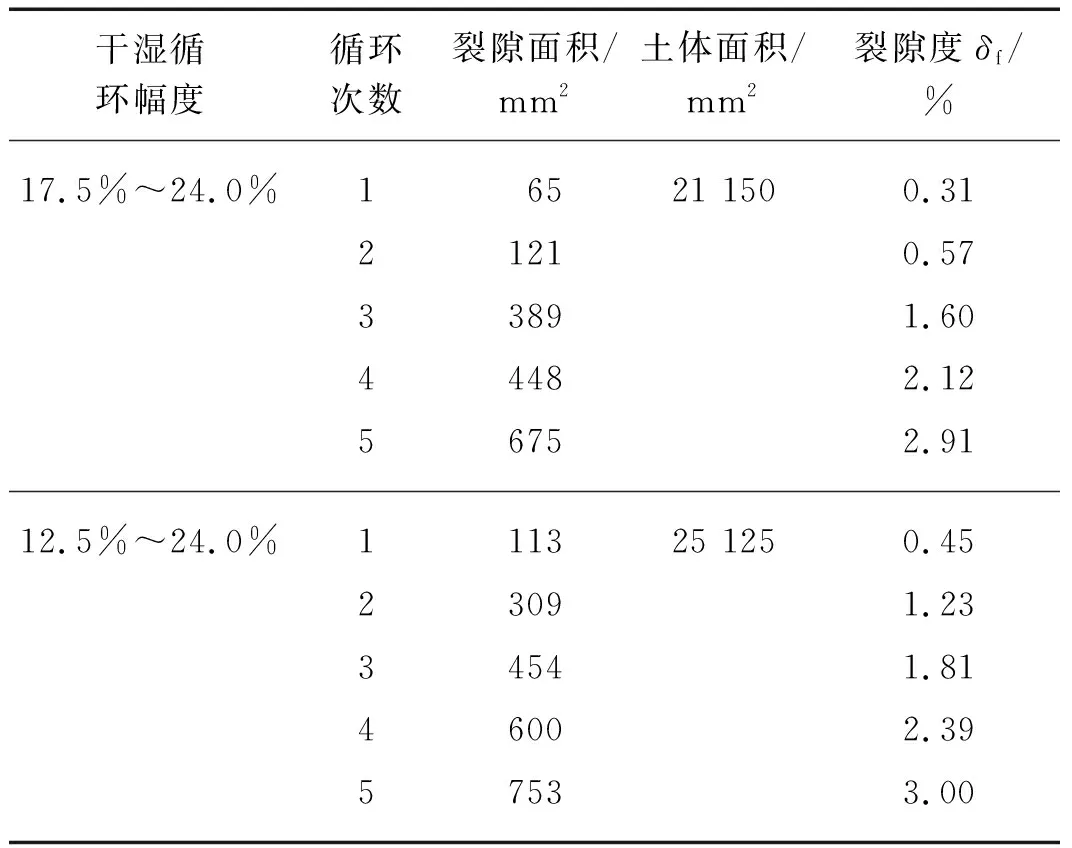
表2 不同循环幅度下的坡顶裂隙参数

由图6可见，裂隙度随着干湿循环次数的增多而增加，但裂隙度增长幅度并没有发生太大的变化.在不同循环幅度下，边坡模型表面的裂隙扩展情况有所不同，大循环幅度下的裂隙度总是比小循环幅度下的裂隙度高，两者之间的差值在第2次干湿循环时达到最大，即0.66%.但随着干湿循环次数的增多，两种情况下的裂隙度相差逐渐减小.

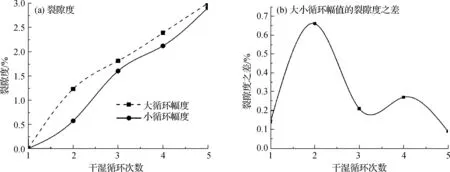
图6 干湿循环作用下裂隙度的变化Fig.6 The change of crack radios under dry-wet cycles

裂隙的存在相当于把土体分割成多个小块，缩短了水分消散的路径，加快水分的蒸发.相比小循环幅度，大循环幅度下不仅水分蒸发的路径变短，含水率的变化更大，造成土体的含水率随路径变化的梯度更大，水分蒸发的速率更快，土体的张拉程度也越大，进一步加速裂隙扩展.

利用曲线拟合得到干湿循环次数与裂隙度的关系式.由图6(a)可以看出，干湿循环次数和裂隙度之间基本呈线性相关，利用线性公式对曲线进行拟合，可得：

δf=k(n-1),

(2)

式中：k为裂隙度随干湿循环次数的增长速率，其受含水率变化幅度影响较大；n为干湿循环次数.两条曲线相关系数R2均大于0.9，拟合效果较好.

2.2 干湿循环作用对土体强度的影响

每次加湿过程完成后在边坡模型上均切取6个环刀样，利用四联直剪仪进行慢剪试验，得到不同垂直荷载下(50，100，200，300，400 kPa)坡面下8 cm深度处的抗剪强度，计算整理得到土样的黏聚力和内摩擦角(图7).

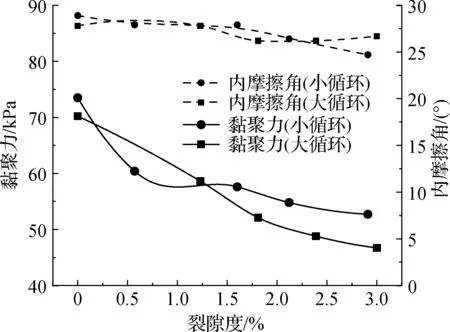
图7 裂隙度和黏聚力、内摩擦角的关系Fig.7 The relationship between crack ratios and cohesion, internal friction angle

由图7可知，随着裂隙的扩展，大循环幅度与小循环幅度相比，前者的黏聚力下降幅度更大.第5次干湿循环后，黏聚力达到最小，且大循环幅度的黏聚力小于小循环幅度的黏聚力；裂隙的扩展对于土体内摩擦角的影响比较小.因此可以利用初始黏聚力c0、循环幅度Δw、裂隙度δf，干湿循环次数n等对试验数据进行拟合，推导裂隙度和土体黏聚力的关系：

首先根据试验条件拟合曲线得到黏聚力和干湿循环次数、干湿循环幅度的关系：

c=c0[1-pΔwln(qn-q+1)]，

(3)

式中p、q为拟合参数.本次试验中大循环幅度取Δw=11.5，小循环幅度取Δw=6.5.初始循环次数为1，n=1时，c=c0，符合黏聚力随循环次数变化的物理含义.然后计算得到大循环幅度拟合参数为：p=0.013 8;q=18.8，小循环幅度拟合参数为：p=0.013 8;q=5.44，可得

大循环幅度黏聚力变化：

c=c0[1-0.16ln(18.8n-17.8)],

(4)

小循环幅度黏聚力变化：

c=c0[1-0.09ln(5.44n-4.44)],

(5)

式中：c0为初始黏聚力(kPa);n为干湿循环次数，n取1,2,3,4,5.

两条拟合曲线的方程相关系数大于0.99，拟合效果较好.利用公式(2)和(3)可以得出，土体黏聚力和裂隙度的关系式：

(6)

式中：p,q,k为干湿循环作用下，黏聚力随裂隙度变化的参数，由试验数据计算得出.其中p,q分别反映干湿循环幅度和干湿循环次数的影响；k反映了干湿循环过程中裂隙扩展对黏聚力的影响.

从式(6)中得知，大循环幅度下边坡土体的含水率变化梯度更高，边坡表面裂隙更多更宽，导致胶结物质流失增加.同时由于裂隙存在，土粒之间相互胶结的面积减小，胶结作用变弱，导致黏聚力下降幅度增加.内摩擦角的变化不大且无规律，这里不做讨论.

2.3 干湿循环作用下裂隙深度的确定

裂隙扩展时，裂隙尖端的水平应力超过土体抗拉强度，而土体的抗拉强度主要来源于颗粒间的黏结和分子引力形成的黏聚力、胶结物质的形成胶结力和表面张力形成颗粒间的吸附力等3种作用力，它与土体含水率、饱和度、基质吸力等有着密切的关系.干湿循环作用下，土颗粒之间胶结物质逐渐流失，土体内部产生微裂隙，导致表面张力和吸附力减小甚至消失.

根据非饱和土的摩尔-库伦强度理论[18]：

(7)

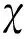
利用试验结果，得到干湿循环作用下黏聚力和裂隙度的关系如式(8)所示：

(8)

式中：c′0为未经过干湿循环且土体基质吸力和净法向应力均为0时的黏聚力.

Lu等[13]认为土体受拉状态下，正应力和剪应力比值和受压状态下保持一致，土体破坏是正应力与剪应力之比达到了极限时剪切破坏的一种表现，此时土体实际的抗拉强度：

(9)

其中σtua为土体实际的抗拉强度.

引入干湿循环影响下黏聚力的变化：

(10)

其中c′为干湿循环影响下，含有裂隙土体的黏聚力.

由Hooke定律可知：

(11)

(12)

其中：σv、σh分别为竖直、水平方向上的应力；μ为泊松比；E为土体的弹性模量；ua、uw分别为孔隙气压力、孔隙水压力.

当土体处于静止或K0状态时：

(13)

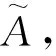
(14)

可得

(15)

(16)

(17)

其中：D为损伤变量，为简便计算令其等于裂隙度.因此，水平应力可以表示为：

(18)

水平应力达到抗拉强度时：土体发生张拉破坏，裂隙开始扩展，因此：

σh-ua=σtua,

(19)

即：

(20)

式中的负号表示规定拉应力方向为负.

假定ua=0，则σv-ua=γ(z-z0)，其中z0表示地下水位深度，γ为土的容量，式(20)可以表示为：

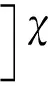
(21)

令与土体性质有关的参量：

(22)

由于土体内部裂隙的损伤参量：

(23)

最后公式化简为：

(24)

利用上述公式确定模型坡顶裂隙深度，以方便后面数值模拟计算.地下水深度和边坡土体尺寸的取值按照模型试验尺寸等比例放大，其他有关土性参数取值与模型试验相同：地下水位深度z0=9.5 m，μ=0.3.由于干湿循环对内摩擦角影响比较小，所以取φ′=26°.分别采用上述推导的裂隙深度计算公式和文献[19]计算公式进行计算，所得对比结果如图 8所示(其中小干湿循环幅度记为SDW)，本文裂隙深度计算结果与参考文献的计算结果相近，说明本文裂隙扩展深度的计算公式合理.

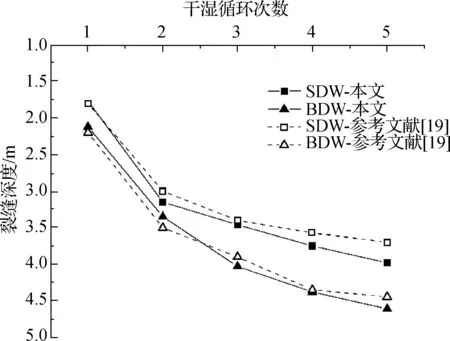
图8 干湿循环次数裂隙深度的关系Fig.8 The relationship between crack depths with dry-wet cycles

由图8可知：裂隙深度随着干湿循环次数的增加而增大，且大循环幅度的影响比小循环幅度更加明显.经历几次干湿循环后，裂隙扩展速率变低，裂隙深度趋于稳定，这是因为土体的抗拉强度主要由黏聚力提供，而干湿循环影响下黏聚力降低，导致其抗拉强度下降.由前文可知，相对于小循环幅度，大循环幅度下的黏聚力下降更大，导致其抗拉强度降低更加显著，相同抗拉强度对应的土体所处部位更深.同时大循环幅度含水率变化梯度大，脱湿过程中相同位置产生更大的基质吸力，在土中产生拉应力，也就更快达到抗拉强度使得土体开裂，最终导致裂隙的扩展.当干湿循环次数不断增加，土中胶结物质流失达到最大，黏聚力下降趋于稳定，裂隙扩展也将逐渐稳定.

3 边坡稳定性分析

采用Geo-studio软件，以模型试验结果为计算参数进行数值分析.以厦门地区气候条件为例[20]，计算暴雨条件下10 h后，经历不同干湿循环后边坡的含水率变化及边坡安全系数，讨论干湿循环造成的裂隙扩展和强度降低对花岗岩残积土边坡稳定性的影响.

3.1 计算模型

采用模型试验测得的土体物理力学参数建立计算模型，几何尺寸按照实际模型试验的尺寸等比例放大10倍，具体尺寸如图9所示：

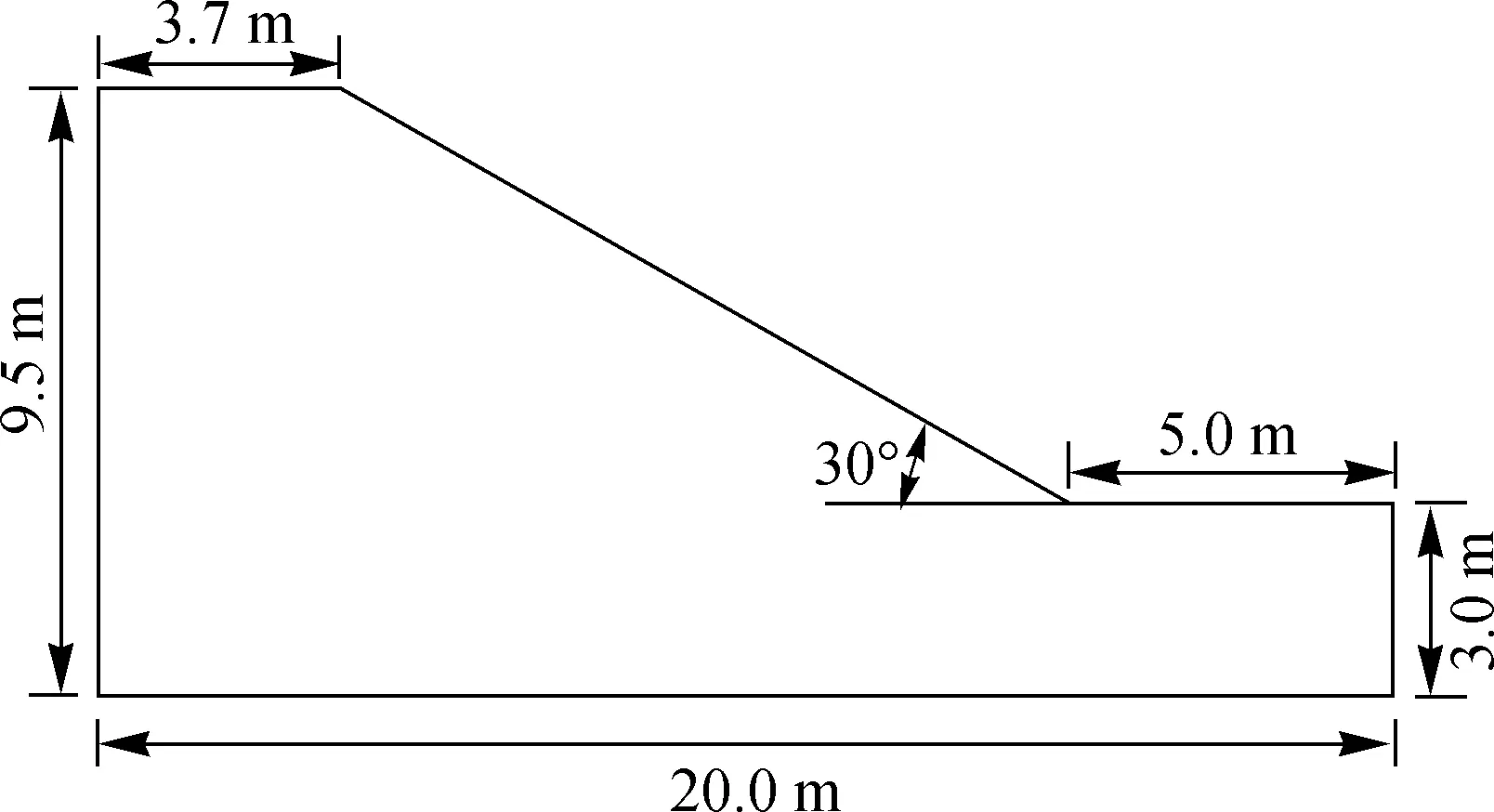
图9 计算模型示意图Fig.9 Schematic diagram of calculation model

考虑随着干湿循环的次数增加，裂隙不断扩展，黏聚力不断降低，会使得土的饱和渗透系数发生变化.根据刘宏泰等[21]的研究成果，确定进行数值模拟时每次干湿循环的渗透系数，如表3所示.

表3 干湿循环作用下土体的渗透系数

3.2 边界条件

1) 降雨边界条件：模拟降雨强度为暴雨，在边坡表面节点施加0 m的孔隙水压，计算中降雨历时10 h.

2) 地下水位边界条件：地下水位在边坡底部，设置模型右边界为透水边界，模拟渗流过程.

3) 裂隙的处理：花岗岩残积土常见的滑坡孕育过程中坡顶几乎都产生张拉裂缝[22]，裂隙所在单元不具有水平抗拉强度.裂隙单元的土体竖直方向的渗透系数相比水平方向的渗透系数扩大3个数量级来模拟裂隙的渗透特性[23].考虑暴雨条件下，土体裂隙中会存在积水，认为雨水充满竖向张裂隙，裂隙范围内存在一个最大影响深度的静水压，作为入渗边界条件施加在模型上.同时，由于裂隙度随干湿循环次数的增加呈线性关系，所以利用增加或者减少张拉裂隙的条数，达到干湿循环次数对应的裂隙面积，以此考虑裂隙影响来计算边坡安全系数.各种工况下的裂隙参数取值如表4所示.

表4 干湿循环作用下裂隙参数

表4中裂隙宽度计算由裂隙度和坡顶土体面积共同决定，裂隙宽度：

W=A坡顶×δf,

(25)

其中：W为裂隙宽度，A坡顶为边坡顶部面积.数值模拟采用二维模型，边坡宽度取单位长度，面积取值为3.7 m2.裂隙深度按照上文所述计算.

3.3 计算结果分析

1) 含水率变化

对比不同干湿循环幅度、不同干湿循环次数的含水率变化如图10所示.经过5次干湿循环，边坡土体经历了反复收缩膨胀，表层土粒重新排列，各个位置的密实度也逐渐趋于一致.随着干湿循环次数增加，各个传感器测得的含水率变化趋向一致，且边坡干燥速率逐渐加快.这主要是由于干湿循环过程中，边坡表面逐渐开展出一些细小裂缝，并逐渐加宽加深延伸至边坡内部，水分蒸发通道增多，蒸发速率加快.对比数值模拟与模型试验的结果，两者变化趋势吻合度较高，可认为数值模拟的结果准确.

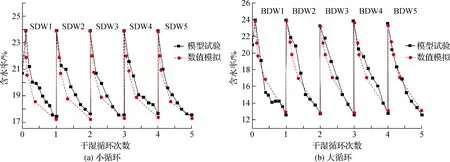
图10 边坡含水率变化Fig.10 Change of slope moisture content

2) 潜在滑裂面位置

由图11所示，干湿循环导致土体发生张拉破坏，潜在滑裂面位置总是沿着张裂隙发展，所有边坡的上滑点都在张裂隙所在的位置.

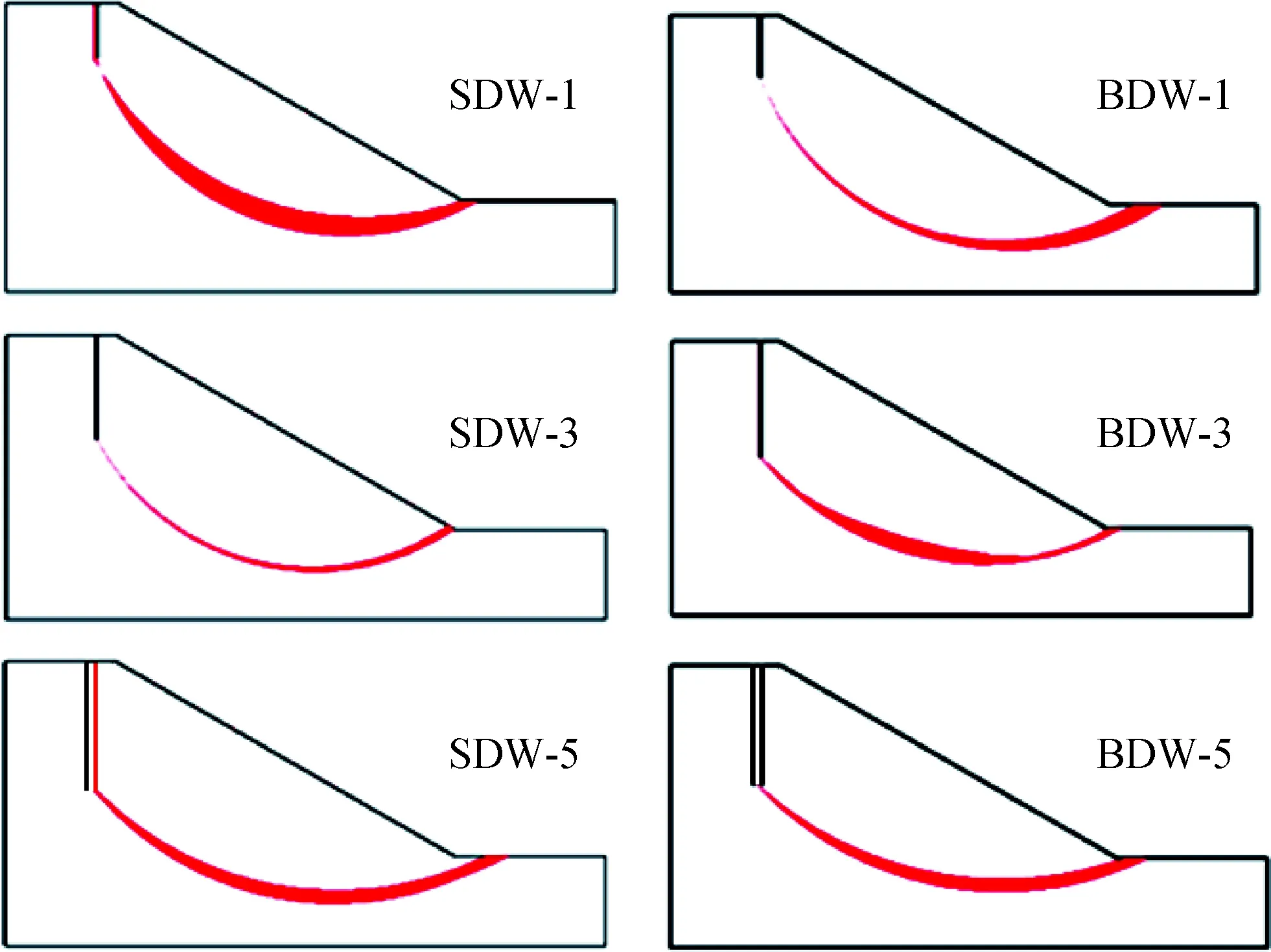
图11 潜在滑裂面位置Fig.11 Location of potential slip plane

3) 安全系数

利用以上条件计算得到暴雨条件下的边坡安全系数随时间的变化关系如图12所示.由图12可知，降雨过程中，边坡的安全系数不断下降，大循环幅度影响下的安全系数总是低于小循环幅度；随着干湿循环次数的增加，裂隙扩展对边坡稳定性的影响增大，在第3次循环达到最大，但当干湿循环次数增加到第5次时，干湿循环幅度对边坡稳定性的影响逐渐降低.随着干湿循环次数增加，不同循环幅度对边坡稳定性的影响趋于相同.

图12 不同工况下安全系数随时间的变化Fig.12 The safety coefficient with time under dry-wet cycles

第5次干湿循环作用后，边坡在降雨8 h后出现安全系数突然下降，这主要是由于土体渗透系数的增大和裂隙的扩展，雨水入渗加快，边坡的非饱和区在降雨8 h后消失，边坡稳定性突然降低，说明降雨影响边坡稳定性的最危险条件为雨水全部浸润整个边坡时，干湿循环作用导致裂隙的扩展，土体强度的降低和渗透性的增加，会加速雨水浸润边坡过程，从而降低边坡的安全储备.