基于滑模观测器的车辆半主动座椅悬架系统H∞最优控制
2022-07-14王小龙黄晋英吕海峰魏成思
王小龙, 黄晋英, 吕海峰, 魏成思
(1.中北大学 机械工程学院,太原 030051;2.北京北方车辆集团有限公司,北京 100072)
货车、工程和坦克装甲车辆运行路况恶劣,行驶时产生的剧烈冲击振动会严重损害乘员的身心健康。近年来发展起来的磁流变半主动座椅悬架具有响应速度快,结构简单,成本低,减振效果接近主动悬架等优点,是车辆振动控制领域的一个研究热点[1-3]。
控制律的设计对于半主动座椅悬架性能的发挥起着重要的作用[4-5]。受不同坐姿人体振动特性差异和磁流变阻尼器性能影响,人体-座椅系统动态特性存在一定的未建模动态、参数不确定性和未知输入,会影响座椅悬架控制系统的性能,因此控制器需要具备一定的鲁棒性来应对模型和振动激励的不确定性[6]。张志勇等[7]考虑座椅悬架系统的参数不确定性,基于座椅加速度设计了H∞输出反馈控制器,但设计的状态观测器测量输出方程中未考虑参数不确定性及未知干扰的影响。Lathkar等基于7自由度人体-座椅-车悬架模型,利用座椅绝对位移构造自适应干扰观测器估计系统模型简化过程中产生的扰动及外界干扰,并设计了直接滑模控制器,但实际工程应用中座椅绝对位移难以直接测量,通过加速度二次积分会引入较大的累积误差。吕振鹏等[8]以天棚控制作为跟踪模型,通过自适应律对干扰进行估计,设计了模型参考自适应模糊滑模控制器,但实际应用中需要额外测量车厢地板绝对位移或振动加速度实时驱动天棚控制动力学仿真模型以获取参考状态。
基于上述分析,本文提出一种可直接工程应用的基于滑模观测器的半主动座椅悬架H∞最优控制方法。滑模观测器基于输出误差等效注入思想进行干扰估计,具有响应速度快和鲁棒性强的优点,目前已有较成熟的设计理论[9-10]。然而,座椅悬架系统通常采用的直接可测量加速度信号中含有系统未建模动态、参数不确定性和未知输入,规范型的滑模观测器设计方法不能直接应用,通过加速度积分构造测量输出方程,放大的量测噪声会导致附加的估计误差。为此,本文通过结合低通滤波技术构造新的增广系统设计滑模观测器,成功实现了座椅悬架系统的集总干扰估计,进而运用H∞控制技术对座椅悬架滑模观测器估计误差和振动输入引起的干扰进行抑制。
1 人体-座椅悬架系统模型
1.1 人体-座椅悬架系统动力学模型
考虑图1所示的人体-座椅悬架系统动力学模型,其中M1~5分别为座椅、人体臀部、人体内脏、上半身躯干与头部的质量;k1~5和c1~5分别为各部分对应的刚度和阻尼;k2c和c2c分别为座椅坐垫的刚度与阻尼。x0~5分别为车厢地板、座椅、人体臀部、内脏、上半身躯干与头部的位移,F为实际的可控半主动作动力。则人-椅悬架系统的动力学方程为
(1)
(2)
(3)
(4)
(5)
1.2 人体-座椅悬架系统简化模型
由于不同人体的坐姿人体动力学参数存在一定的差异,图1所示的人体-座椅悬架系统模型难以直接应用于控制器设计,需要对其进行简化。对式(1)~(5)进行相加合并,可得
(6)
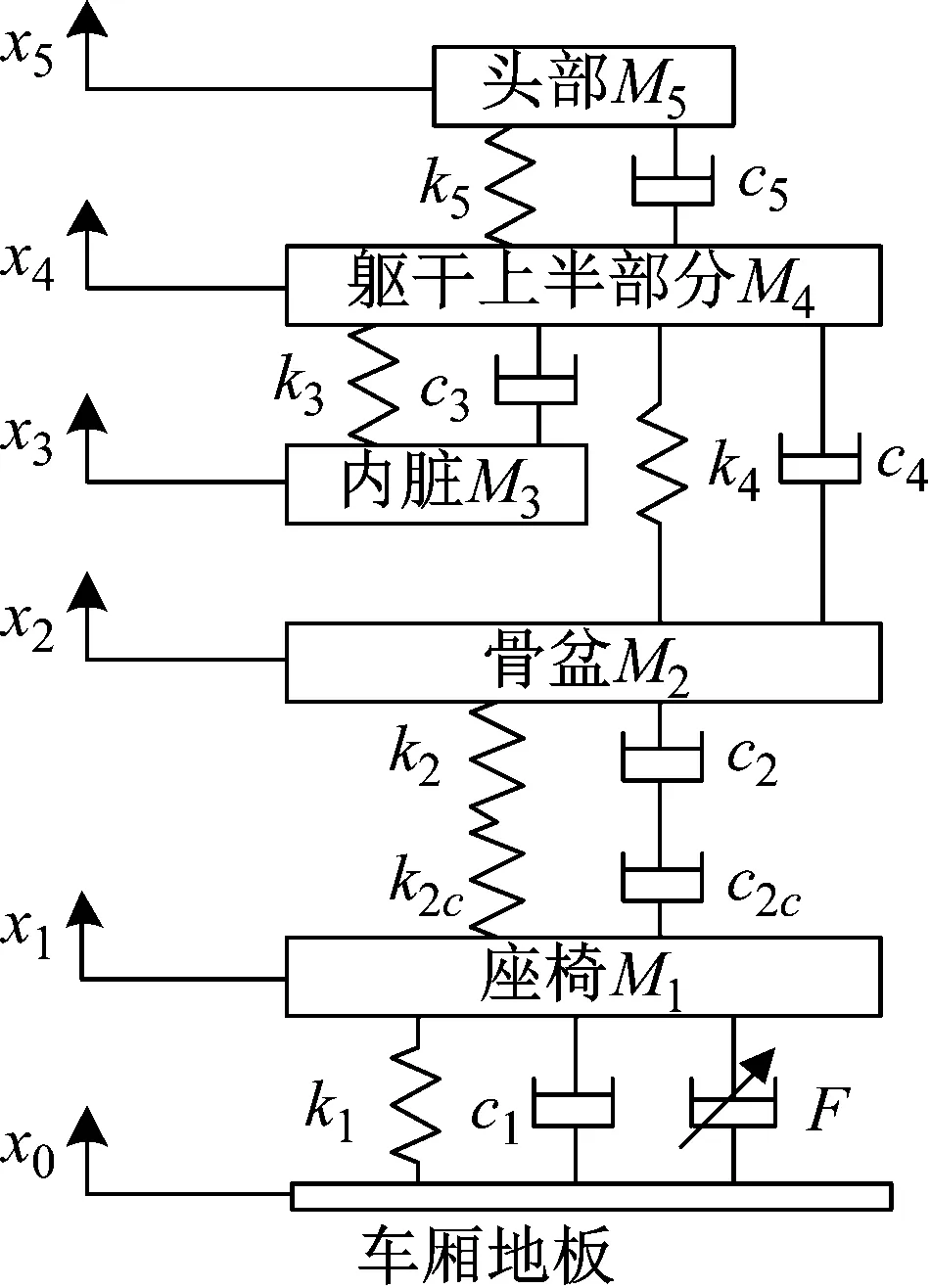
图1 人体-座椅悬架系统模型Fig.1 Seat-driver suspension system model
由于式(6)中M2~5未知、x2~5不可测,并考虑到实际座椅悬架系统存在未建模动态、作动器存在模型失配误差即F=u+ΔF,系统(6)可进一步写为
M=M1+M2+M3+M4+M5
(7)
式中:u为由控制器得到的已知控制力;Δfd0为座椅悬架系统未建模动态;ΔF为作动器模型失配误差。
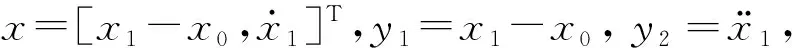
(8)
其中
fd=ΔF+fd0+Δfd为人体-座椅悬架系统集总干扰。
2 人体-座椅悬架系统滑模观测器设计
由于系统(8)中直接可测量加速度含有未知干扰fd,不是滑模观测器设计的规范型(规范型可测输出方程形式为y=Cx或y=Cx+Du),因此借鉴文献[9]中对传感器故障估计的处理方法,将含有未知干扰的加速度y2通过如下低通滤波器构造辅助变量
(9)
式中,Af为低通滤波器参数。
合并(8)和(9)得
(10)
则系统(10)可进一步写为
(11)
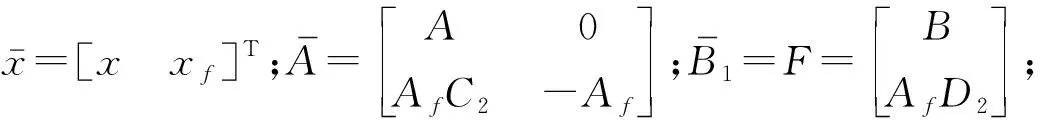
则针对系统(11)可设计如下滑模观测器
(12)
(13)
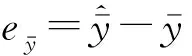
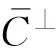
与矩阵正交三角分解(QR分解)对系统(11)进行坐标变换可得到如下干扰解耦系统
(14)
其中系统矩阵具有如下形式
进一步利用如下非奇异矩阵
(15)
对系统(14)进行坐标变换使其具有如下形式
(16)
其中系统矩阵为
对未知干扰解耦的系统(16)设计如下滑模观测器
(17)
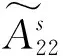
(18)
由式(16)和式(17)相减可得到观测器误差动态
(19)
(20)
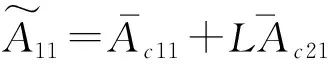
(21)
(22)
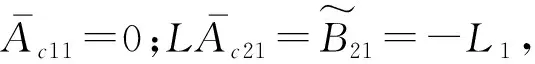
青海共和盆地沙区是我国荒漠化危害严重的地区之一,青海省治沙试验站于1959年开始在青海省共和县沙珠玉地区进行一系列的沙漠化防治工作,总结出了一些有效的高寒沙区植被恢复综合技术,并在青海省推广成功的治理模式和经验,产生了积极的带动和辐射作用。
(23)
要使(23)稳定,则需L1>0,并且L1越大,对干扰的增益也越大。如系统(23)为高阶系统,则可利用H∞技术设计观测器增益L1对干扰进行抑制。但实际系统(23)为一阶系统,可直接选择适宜的观测器增益L1,可使|e1|≤μ,其中μ=max(|e1|)>0。
(24)
结合式(18),可得
(25)
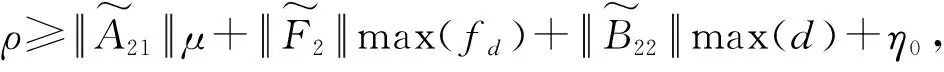
(26)
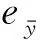
(27)
3 人体-座椅悬架系统干扰重构
(28)
其中
(29)
由于d≠0,如利用输出误差等效注入概念,得到的未知阻尼力估计
(30)
(31)
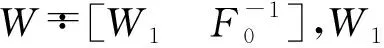
将式(28)写为
(32)
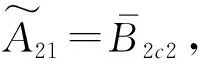
(33)
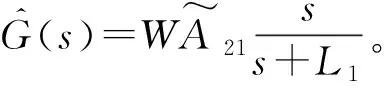
4 人体-座椅悬架系统H∞最优控制
针对系统(8),由于干扰项可由式(31)进行估计,并考虑到干扰估计误差与干扰d在同一个通道,则对系统(8)对应的名义系统:
(34)
设计H∞最优控制器可同时抑制d和fd估计误差对人体-座椅悬架系统的不利影响。
定义最优性能指标
(35)
并取值函数
(36)
则系统(34)的最优控制律为:
u0(x)=-R-1B1Px=-Kx
(37)
其中正定矩阵P为如下博弈代数黎卡提方程[11]的解
(38)
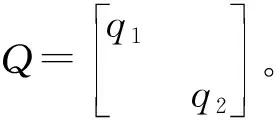
(39)
5 仿真分析
为了考察系统的性能,分别在冲击和随机路面激励[12]路面下经1/4车辆悬架滤波后作为人体-座椅悬架系统的输入进行测试。
冲击激励的数学模型为
zr=zb[1-cos(wrt)]
(40)
式中:wr=2πv/D;zb为半弓高(0.035 m);D为弓宽(0.8 m),并假设汽车以匀速v=0.8 m/s通过。
随机路面的数学模型为
(41)
式中:q(t)为路面不平度位移输入;车速v=30 m/s;wE(t)为白噪声,其强度为2σ2αv;σ=22 mm;α=0.09 m-1。
路面输入与1/4车辆悬架的车厢地板的传递率为
(42)
其中Δ=msmus4+(mscs+mucs)s3+(msks+ksmu+ktms)s2+cskts+kskt。
仿真中人体-座椅悬架系统的模型参数同文献[8],低通滤波器(42)中的参数选择如下:ms=240 kg,mu=36 kg,ks=16 000 N/m,cs=800 Ns/m,kt=160 000 N/m。
滑模观测器和控制器参数选择如下
δ=0.1,ρ=5 000,q1=1.5×105,q2=5e3,
R=0.002,γ=0.5。
5.1 滑模观测器干扰估计效果
图2和图3分别为冲击激励和随机路面激励下的干扰估计效果,冲击激励下的干扰估计误差最大值为0.48 N;随机路面激励下的干扰估计误差最大值为5.47 N,表明扰动可以被滑模观测器精确重构。由于参数摄动引起的不确定性、作动器未知输入与人体-座椅悬架系统的未建模动态在同一个通道内,都可以利用滑模观测器对其进行估计和补偿。
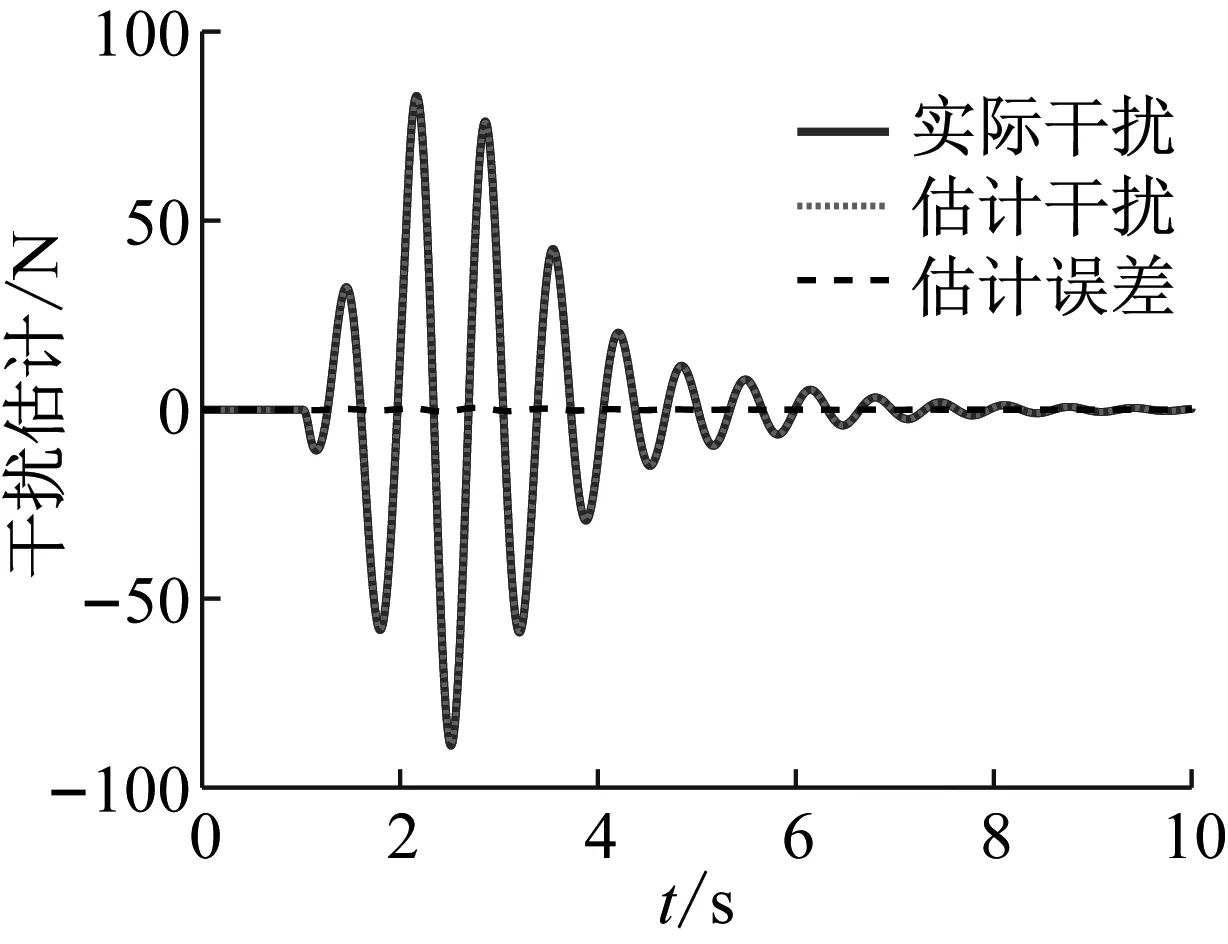
图2 冲击激励下的干扰估计Fig.2 Disturbance estimation under bump excitation
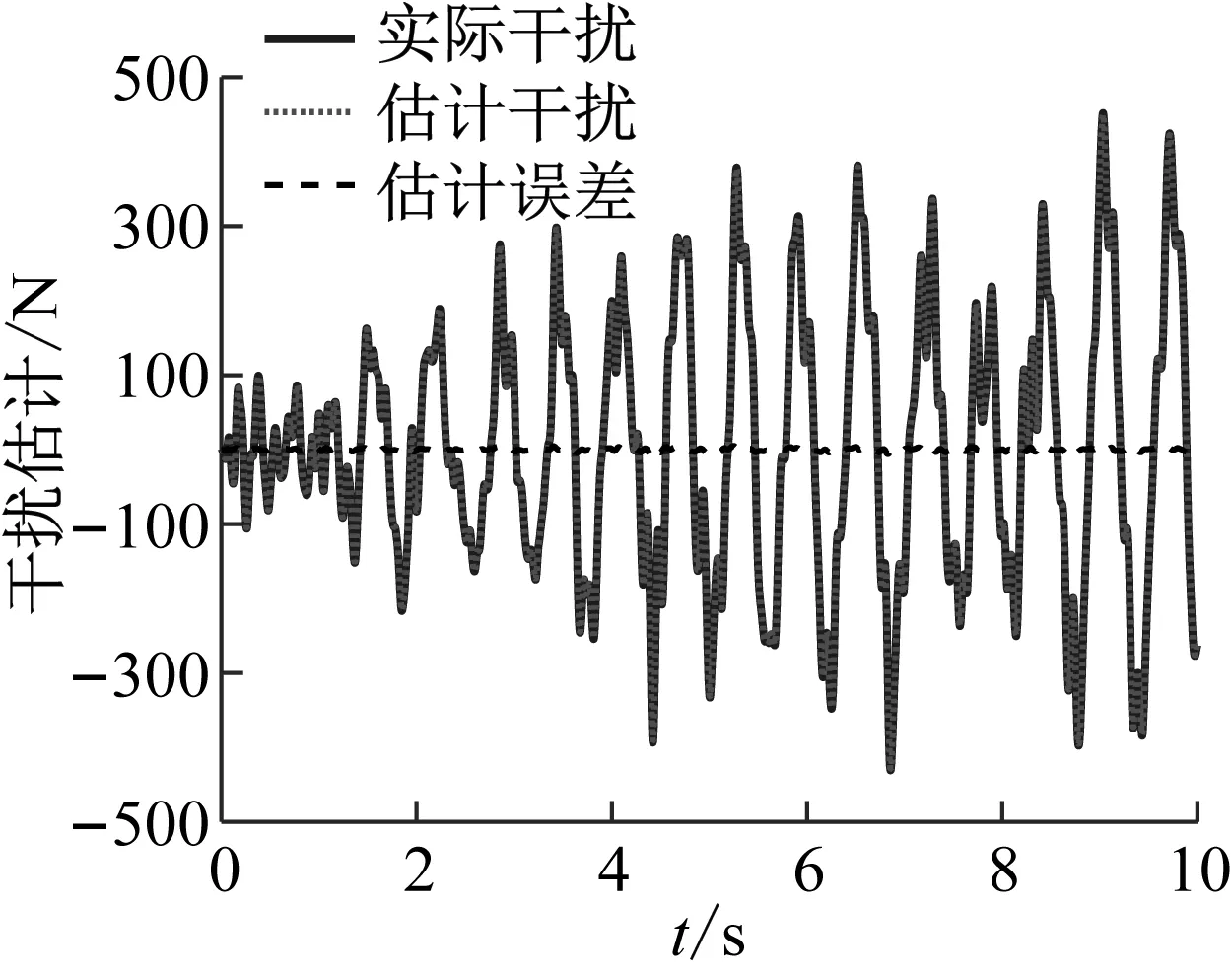
图3 随机路面下的干扰估计Fig.3 Disturbance estimation under random road excitation
5.2 控制效果
图4和图5分别为冲击激励下人体加速度和座椅悬架的位移,图6为由式(35)定义的性能指标。从图可以看出,带有滑模观测器干扰补偿的H∞控制相比无补偿的H∞控制和无控制座椅悬架在性能上有了较大的改善,人体加速度峰峰值分别降低了18.9%和27.9%;座椅悬架位移峰峰值分别降低了24.7%和36.1%,性能指标分别降低了22.7%和47.9%。
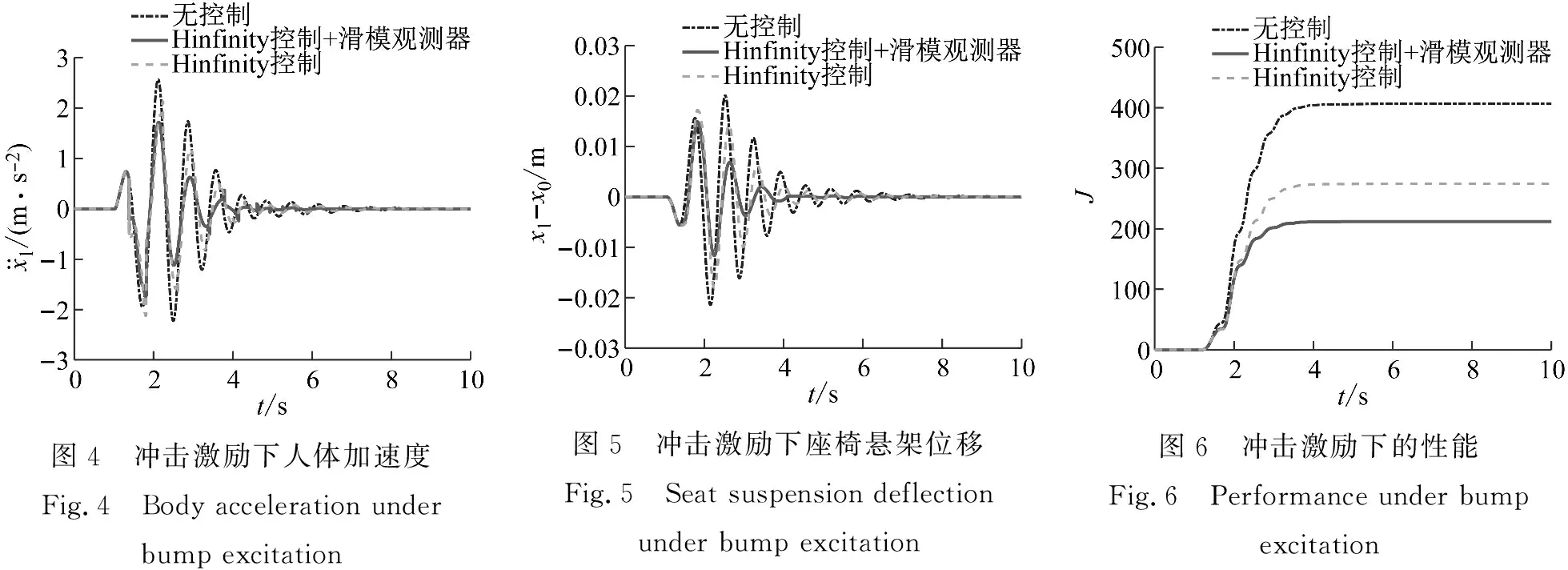
图7和图8分别为随机路面激励下人体加速度和座椅悬架的位移;图9为人体加速度的功率谱密度;图10为随机激励下的性能指标。ISO2631标准规定的人体加速度频率加权均方根值、座椅悬架位移均方根、座椅有效幅值传递率(seat effective amplitude transmissibility, SEAT:人体与车厢地板加速度频率加权均方根值之比)和性能指标见表1所示。随机激励下带有滑模观测器干扰补偿的H∞控制相比无补偿的H∞控制和无控制座椅悬架人体加速度频率加权均方根值分别降低了12.5%和29.3%;座椅悬架位移均方根分别降低了36.8%和50.0%;SEAT分别降低了7.8%和22.4%;性能指标分别降低了55.2%和25.0%。
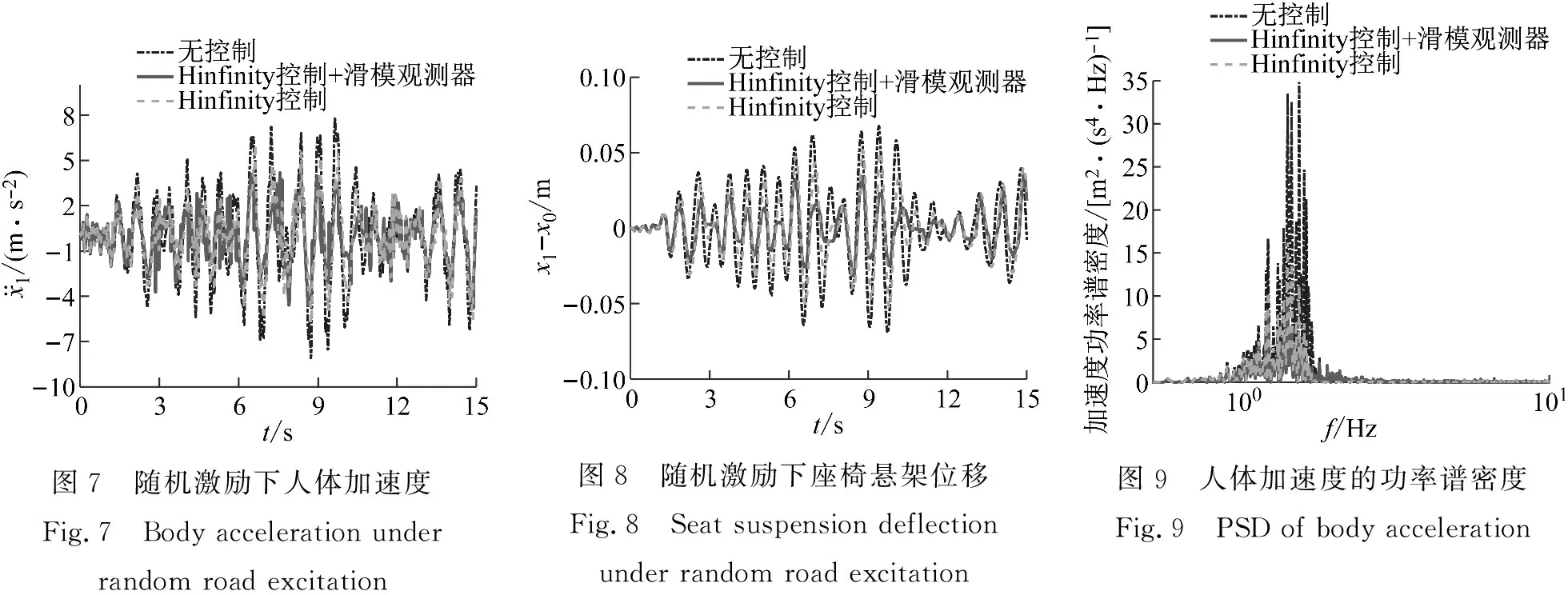
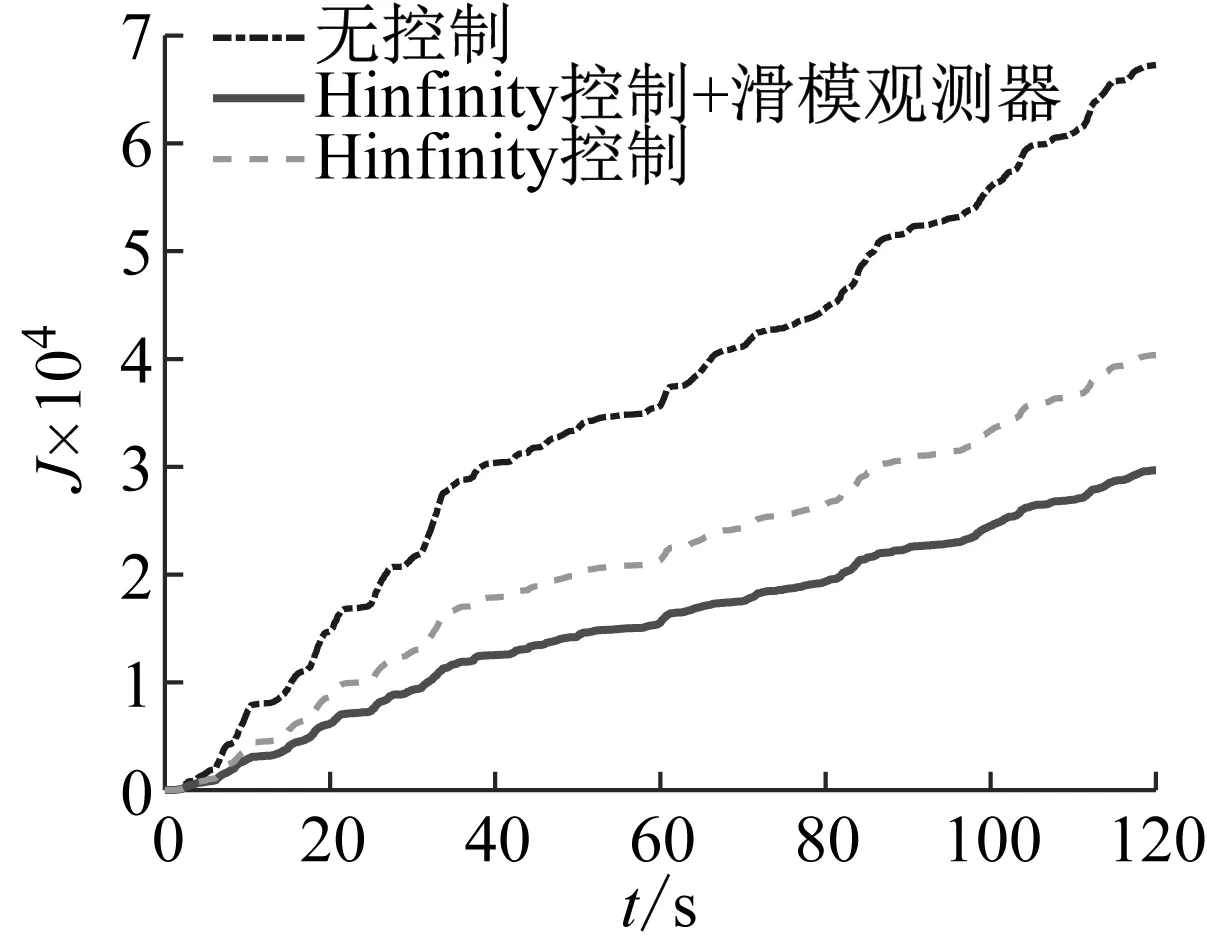
图10 随机路面激励下的性能Fig.10 Performance under random road excitation
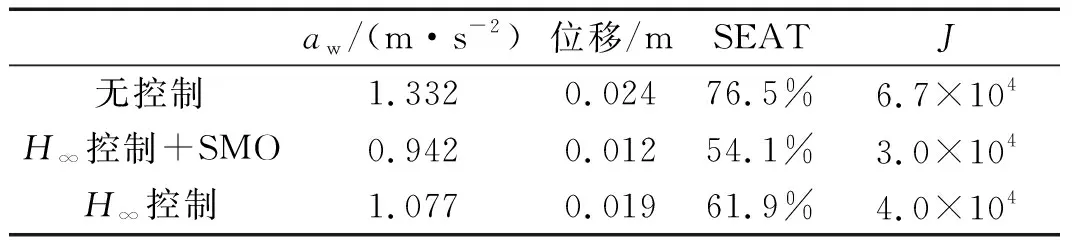
表1 随机激励下的性能Tab.1 Performance under random road
冲击和随机路面激励下的仿真结果都表明提出的带有滑模观测器的H∞控制相比单独H∞控制更能够显著提高座椅悬架的乘坐舒适性。
6 结 论
(1) 通过对座椅悬架系统直接可测量加速度低通滤波构造辅助变量建立增广系统,通过滑模观测器成功实现了对座椅悬架系统未建模动态、参数不确定性和作动器未知输入构成的集总干扰的精确估计。
(2) 由于系统集总扰动为匹配干扰,可通过滑模观测器技术进行精确估计,进而设计控制器补偿。
(3) 通过冲击工况和随机路面仿真分析,基于滑模观测器干扰补偿的H∞最优控制相较单独H∞控制具有更好的控制性能和乘坐舒适性。
