二阶非线性中立型阻尼微分方程的振动定理
2022-07-14曾云辉罗李平俞元洪罗慧慧
曾云辉, 罗李平, 俞元洪, 罗慧慧
(1. 衡阳师范学院 数学与统计学院, 湖南 衡阳 421002; 2.中国科学院 数学与系统科学研究院, 北京 100190;3. 衡阳师范学院南岳学院 数学与计算科学系, 湖南 衡阳 421008)
起源于偏微分方程的Emden-Fowler型泛函微分方程在科学理论研究和工程技术应用中发挥着重要作用,带有阻尼项的二阶中立型Emden-Fowler方程更为广泛,已被应用在天体物理,气体动力学,高速计算机无损传输,智能机器人设计和神经动力系统理论与工程等高新技术领域中[1-3]。
考虑二阶中立型非线性阻尼微分方程
(a(t)φα(z′(t)))′+b(t)φα(z′(t))+
q(t)φβ(x(σ(t)))=0
(1)
其中t≥t0,a(t),b(t),p(t),q(t),τ(t),σ(t)∈C([t0,∞),R),且
z(t)=x(t)+p(t)x(τ(t))
(2)
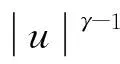
(3)
本文总假设下列条件成立:
(C1)a(t)>0,a′(t)+b(t)≥0,q(t)≥0,q(t)不恒等于0;
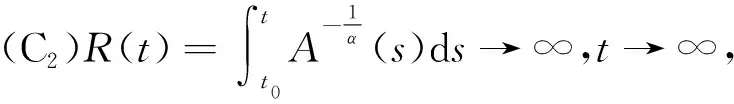
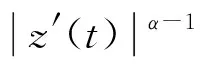
近年来,二阶中立型微分方程解的振动性研究受到广泛关注,取得了许多重要结果。例如,可以参看文献[4-25]及其引文。但是,我们注意到其中大多数文献的振动结果是关于无阻尼方程的,而对于阻尼方程的振动结果较少。我们可参看文献[6],[10]和[20]。而且,这些结果是在方程中立项系数p(t)满足有界的条件下得到的,此意味着上述文献中的振动定理不能应用于当t→∞时,p(t)→∞的情况。最近,Tunc等研究了方程(1)当α=β=1时,即线性二阶中立型方程的振动性。Grace等研究了方程(1)当α=β时,即半线性二阶中立型阻尼方程的振动准则。Bohner等给出了方程(1)当α=1,β>0时,即二阶中立型Emden-Fowler阻尼方程的振动定理。本文的第一个目的是建立方程(1)对任意α>0和β>0成立的振动定理。它们改进,推广和统一了文献[6],[10],[20]的有关结果。并且将二阶线性方程经典的Leighton振动定理[26]推广到二阶中立型阻尼微分方程(1)。
最近,Jadlovska等考虑了方程(1)的特例
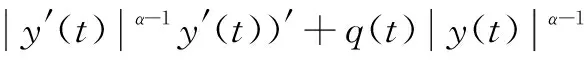
(4)
上式即为(1)中当p(t)=0,b(t)=0和α=β的情况,作者介绍了(4)中当σ(t)=t时经典的Kneser振动准则如下:
定理1.1设
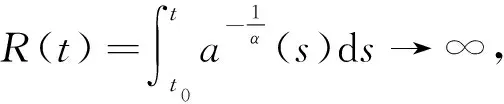
作者在文献[11]中改进了定理1.1从σ(t)=t到σ(t)≤t,他们得到:
定理1.2设
则方程(4)振动。
本文的另一个目的是推广文献[11]的结果到中立型阻尼微分方程
(a(t)φα(z′(t)))′+b(t)φα(z′(t))+
q(t)φα(x(σ(t)))=0
(5)
其中z(t)=x(t)+p(t)x(τ(t)),p(t)≥0。方程(4)是方程(5)中p(t)=0,b(t)=0时的特例。
在下面第1章中我们将给出0≤p(t)<1时的振动结果,在第2章中给出p(t)≥1的振动结果。
下面出现的函数不等式,均假设是最终成立。如通常一样,不失一般,我们仅处理方程的最终正解。
1 当0≤p(t)≤1时的振动结果
本节我们假设:
(C3) 0≤p(t)≤1;
我们需要下面的辅助结果:
引理2.1设x(t)是方程(1)的最终正解,则z′(t)>0。
证设x(t)是方程(1)的最终正解。则存在t1≥t0,使得当t≥t1时有x(t)>0,x(τ(t))>0和x(σ(t))>0。故由(1)和(2),我们有z(t)>0且
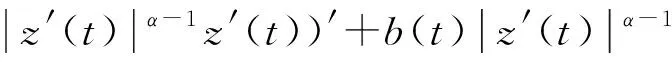
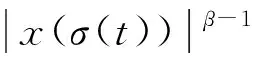
即
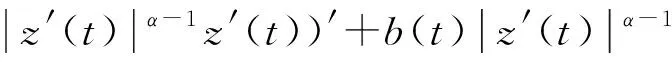
t≥t1
故有
(6)
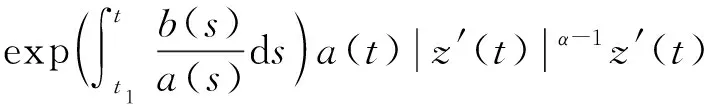
(i)z′(t)>0,t≥t2;(ii)z′(t)<0,t≥t2
下面证明情况(ii)不可能成立。为此,设z′(t)<0,t≥t2。令
(7)
则由式(6)知,存在常数C>0,使得
-A(t)(-z′(t))α≤-A(t2)(-z′(t2))α=-C<0,
t≥t2
即
(8)
对式(8)从t2到t积分,我们得到
令t→∞,由(C1)得z(t)→-∞。此与z(t)>0矛盾。引理2.1证毕。
引理2.2设λ>0,D>0,则
引理2.3设σ(t)≤t,x(t)是方程(1)的最终正解。令
(9)
则我们有
(10)
其中A(t)的定义见(2.2),λ=min{α,β},0 (11) (12) 证明设x(t)是方程(1)的最终正解,则由引理2.1知z′(t)>0。故z(t)是增函数。由式(2),我们有 x(t)≥(1-p(t))z(t),t≥t2 (13) 由引理2.1和式(13),方程(1)成为 (a(t)(z′(t))α)′+b(t)(z′(t))α+q(t)(1- p(σ(t)))βzβ(σ(t))≤0 (14) (A(t)(z′(t))α)′+Q(t)zβ(σ(t))≤0 (15) 其中A(t)见(C2),Q(t)由式(11)定义。 从式(15)和u(t)的定义式(9),我们有 t≥t2 (16) 现分两种情况考虑式(16):α≤β和α>β。 (i) 若α≤β,由式(15)知A(t)(z′(t))α是非增。因σ(t)≤t,故有 A(t)(z′(t))α≤A(σ(t))(z′(σ(t)))α 即 (17) 联合式(16)和(11),我们有 mα,t≥t2,我们得到 (18) (ii) 若α>β。由式(15)得(A(t)(z′(t))α)′≤0。再由(C1),即a′(t)+b(t)≥0,我们得到z″(t)≤0,则有z′(t)≤z′(σ(t))。因此,式(16)产生 (19) 式(19),我们得到 (20) 现式(18)和(20)可统一写为 (21) 其中Q(t),θ(t)的定义见式(11)。λ=min{α,β},且 m=min{mα,1,mβ} (22) 引理2.3,证毕。 定理2.1设(C1)~(C4)成立且σ(t)≤t。若存在ρ(t)∈C1([t0,∞),R+),使得 (23) 其中A(t),Q(t)的定义见式(15),θ(t)见式(12),0 证明:设x(t)是方程(1.1)的最终正解,且σ(t)≤t。则由引理2.3,我们有式(10)成立。以ρ(t)乘式(10)两边且从t2到t积分,我们得到 (24) 对上式右端积分的被积函数,利用引理2.2的不等式,我们有 令t→∞,我们得到上式与(23)矛盾。定理2.1证毕。 推论1(Leighton型振动准则)设 (25) 证明:只需在(23)中取ρ(t)=1即可。 注2.1。 对于二阶线性微分方程 (r(t)x′(t))′+q(t)x(t)=0,t≥t0 (26) 有Leighton振动准则:设 (27) 则方程(26)振动。 显然,当方程(1)简化为(26)时,推论2.1的条件即为条件(27)。因此,推论2.1是Leighton准则的精确推广,同时,它也改进和推广了文献[3]的定理4,放宽了其条件(19),也改进了文献[6],文献[7],文献[9]和文献[23]的定理2.1。 例2.1考虑Emden-Fowler阻尼时滞微分方程 (28) 方程(28)是Bohner等在文献[6]中考虑的例2.4,文中利用定理2.1证明了式(28)的每一解振动或者渐近趋向于零,对一切β>1成立,我们容易证明条件(C2)和式(25)满足,故由推论2.1可以得知方程(28)对一切β>0每一解是振动的。因此,推论2.1改进了文献[6]的定理2.1,而且推论2.1还可应用于方程(1)。但文献[6]的结果不能用于方程(1)。 例2.2考虑中立型时滞微分方程 (29) 方程(29)是文献[14]中考虑的方程(2.14),作者利用推论2.2证明了当q0>1.588 56时方程(29)振动。而利用文献[2]的推论2,要求q0>5.443 81才能保证方程(29)的一切解振动。 因此,由定理2.1可得当q0>1.5时,方程(29)振动。故定理2.1改进了文献[12]的推论2.2,也改进了文献[5]的推论2。 下面的定理是方程(5)的Kneser型振动定理。 定理2.2设(C1)~(C4)成立,σ(t)≤t。 若 (30) 则方程(5)振动。 其中R(t)和A(t)由(C2)定义,Q(t)由式(11)定义。 证明因当α=β时,方程(1)即为方程(5),故我们只须证明条件(30)成立保证了当α=β时条件(23)成立即可。 现设式(30)成立,则存在ε>0使得对一切充分大的t,有 (31) (32) 对上式从充分大的T>t0到∞积分,产生 dt=∞ (33) 另一方面,当α=β时,有λ=α,m=1,Q(t)=σ(t)。我们在式(23)中取ρ(t)=Rα(σ(t)),即得式(33)成立。 定理2.2证毕。 例2.3考虑半线性时滞微分方程 (34) 方程(34)是文献[21]中考虑的方程(7), 作者利用该文的定理3得到当条件 q0>1.929 16 (35) 成立时, 方程的一切解振动。 因此, 当 q0>0.163 1 (36) 成立时, 条件(30)满足, 则由定理2. 2知方程(34)振动。 故定理2.2推广和改进了文献[21]的定理3。 注2.3定理2.2推广了定理1.1和定理1.2。 我们将最近文献[11]的Kneser型振动定理从时滞微分方程推广到中立型微分方程。定理2.2给出的是中立项系数p(t)有界时的振动结果。 下面考虑p(t)无界时的情况。 本节假设: (C5)p(t)≥1且最终不恒为1; 引理3.1设σ(t)≤τ(t),x(t)是方程(1)的最终正解。 令 (37) 则 (38) 其中 (39) (40) 证明设x(t)是方程(1)的最终正解。 由引理2.1,有z′(t)>0,即z(t)是增函数,由假设得 (41) 因τ(t)>t且是增函数,故有τ-1(t)>τ-1(τ-1(t)),于是有z(τ-1(t))>z(τ-1(τ-1(t)))。利用(40)和(41)得到x(t)≥P*(t)z(τ-1(t))。由(C6),我们有 x(σ(t))≥P*(σ(t))z(g(t)) (42) 因σ(t)≤τ(t),故有τ-1(σ(t))≤t或g(t)≤t。因此,方程(1)给出 zβ(g(t))≤0 (43) (A(t)(z′(t))α)′+Q*(t)zβ(g(t))≤0 (44) 其中A(t)见式(7),Q*(t)见(39),g(t)由(C6)定义。 我们注意到(37)的ξ(t)与(9)的u(t)类似,不等式(44)和不等式(15)类似。 因此,可以用推导不等式(10)的方法来推导不等式(38),故省略。 引理3.1证毕。 引理3.2设σ(t)≥τ(t),x(t)是方程(1)的最终正解。 令 (45) 则 (46) 其中0 证明因σ(t)≥τ(t),故τ-1(σ(t))≡g(t)>t,类似引理3.1,由式(1),(43)和(44),我们得到 zβ(t)≤0 (47) 和 (A(t)(z′(t))α)′+Q*(t)zβ(t)≤0 (48) 剩下的证明类似于引理3.1,故省略。 引理3.2证毕。 定理3.1设(C1),(C2),(C5),(C6)成立,若存在ρ(t)∈C1([t0,∞),R+)使得当σ(t)≤τ(t)时,有 (49) 当σ(t)≥τ(t)时,有 (50) 其中λ,K,L,A(t),Q*(t),g(t),θ1(t)的定义均可见引理3.1和引理3.2,则方程(1)对任意α>0,β>0都是振动的。 证明设x(t)是方程(1)的最终正解,由引理2.1得z′(t)>0。因σ(t)≤τ(t),故τ-1(σ(t))=g(t)≤t。令 (51) 则由引理3.1,我们有 (52) 用ρ(t)乘式(52),从T到t积分,我们得到 (53) 对式(53)右端被积函数利用引理2.2,产生 (54) 在(54)中令t→∞,我们得到与(49)矛盾。 现考虑σ(t)≥τ(t)。利用引理3.2,令 (55) 则有 (56) 用ρ(t)乘(56),从T到t积分,我们有 (57) 对(57)右端被积函数利用引理2.2,我们得到 (58) 上式中令t→∞,我们得到与(50)矛盾。 定理3.1证毕。 在定理3.1中取ρ(t)=1,我们有 推论3.1(Leighton型振动准则)设 (59) 其中Q*(t)由(39)定义,则方程(1)振动。 下面的例子说明定理3.1的应用。 例3.1考虑中立型阻尼微分方程 (60) 下面给出p(t)无界时方程(5)的Kneser型振动准则。 定理3.2设(C1),(C2),(C5)和(C6)成立,当σ(t)≤τ(t)时,有 (61) 当σ(t)>τ(t)时,有 (62) 则方程(5)振动,其中R(t),A(t)定义见(C2),g(t)定义见(C6),Q*(t)定义见(39)。 证明由于定理3.1,定理3.2分别与定理2.1,定理2.2类似,后者都是利用前者来证明,方法是一样的。 故省略。 定理3.2证毕。 例3.2考虑二阶半线性中立型阻尼方程 t≥1 (63) 下面验证(61): 故当 (64) 我们有(61)成立,利用定理3.2知方程(63)对任意α>0都振动。 本文有两个目的,一是推广经典的Leighton振动准则和Kneser振动准则。另一个是给出二阶非线性中立型阻尼微分方程(1)的新振动准则,使得既能适合Emden-Fowler方程,又能用于半线性微分方程,从而改进、推广和统一了若干文献中的新结果。最近,Jadlovska和Dzurina在文献[8]中将Kneser振动准则推广到二阶半线性时滞微分方程,本文定理2.2和定理3.2进一步将文献[8]的结果推广到中立型阻尼微分方程。我们不仅考虑中立项系数p(t)有界,而且也考虑了p(t)可以趋向于无穷的情况,我们得到的Leighton型振动准则,也考虑了p(t)→∞(t→∞)的情况。上述结果在文献中是没有出现过的。本文给出的例子也说明所得结果是新的。 即文献中的振动定理或者不能适用,或者所得结果不如我们的定理精确。本文是在假设(C2)成立条件下,即方程是正则型的。我们下一步将考虑(C2)不成立的情况,即方程是非正则型的。欢迎有兴趣的同行一起合作和交流。

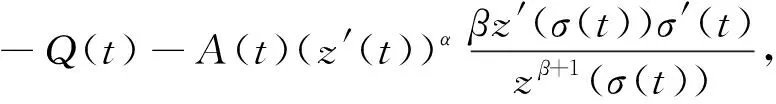

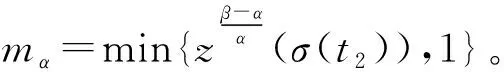
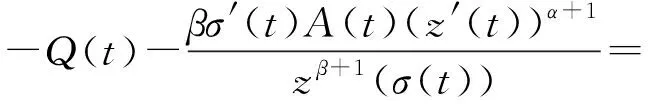
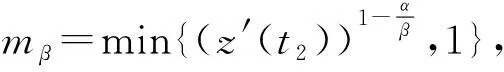


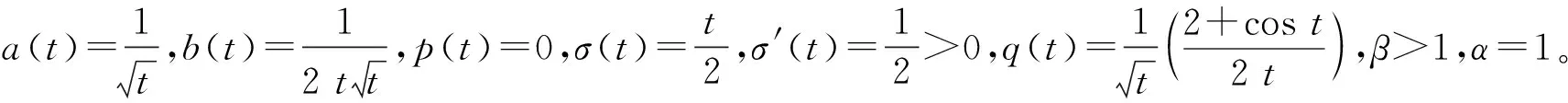
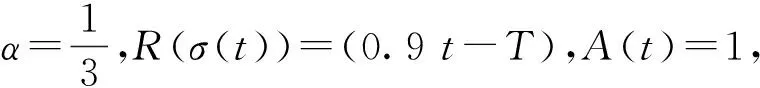
2 p(t)≥1时的振动结果
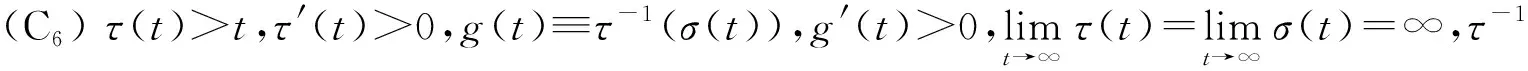
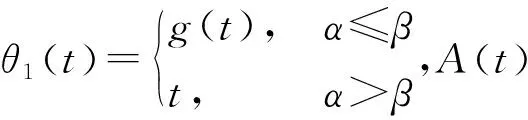
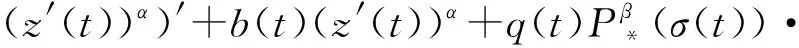
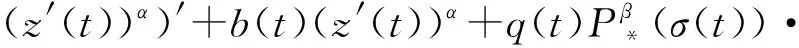


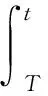


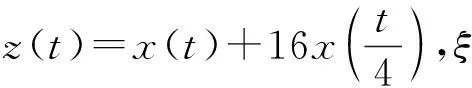
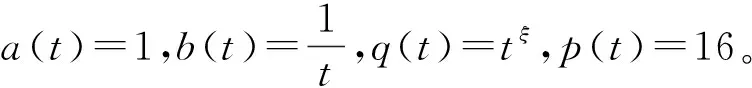

3 结 论
