人工智能在空腔气动/声学特性预测与控制参数优化中的应用

吴军强，杨党国,，张林，龚天弛，周方奇，王岩，李阳

1.中国空气动力研究与发展中心 空气动力学国家重点实验室，绵阳 621000

2.中国空气动力研究与发展中心 高速空气动力研究所，绵阳 621000

3.南京航天航天大学 航空学院，南京 210016

0 引 言

飞行器气动特性快速精准预测不仅在飞行器气动、总体和结构设计中起着至关重要的作用，还是飞控系统设计与完善、飞行仿真、性能评估及飞行试验可靠实现的基本前提和重要保障。针对不同的研究目标，飞行器气动特性预测所采用的模型主要分为两大类：一类是基于理论分析并结合一定的试验或CFD 模拟结果建立的具有明确数学表达式的气动模型，如应用于飞行器气动力建模的代数模型、阶跃响应模型和状态空间模型等，该类模型物理意义清晰、适用范围明确，但在精确处理和预测非定常非线性条件下的气动特性时存在一定困难；另一类是基于数据驱动的智能学习算法类气动模型，如支持向量机、模糊算法、遗传算法、人工神经网络等。其中，基于人工神经网络的机器学习技术具有多输入多输出特性以及精确描述任意复杂度函数的能力和能够充分利用大数据挖掘实物本质特征的能力。

近年来，机器学习与流体力学交叉融合引起了众多研究者注意，并在气动优化设计、湍流模型改造、极端约束条件下气动数据预测、复杂流场重构和非定常气动力建模等领域进行了富有创新性和前沿性的探索。为充分发挥机器学习方法强大的表征能力及其在飞行器气动特性预测方面的优势，进一步挖掘现有飞行器风洞试验数据库的潜在价值，本文以高速复杂流动条件下飞行器空腔为研究对象，对空腔气动特性和噪声载荷数据进行智能分析，构建多参数条件下的空腔噪声载荷智能预测控制模型。

空腔流动是空气动力学研究领域的一个经典模型和热点问题，广泛存在于航空航天装备中（如飞机弹舱、起落架舱、舰船舱体、燃烧室、缝隙和凹槽等），高速空腔流动机理及噪声控制研究对空腔结构设计和腔内设备安全评估具有重要意义，自20世纪50年代以来就吸引了众多学者的注意。相关研究指出，空腔噪声在一定条件下可达170 dB，对应均方压力幅值6 300 Pa，流动出现自持振荡，引发流声耦合现象，容易导致飞行器内部结构的疲劳损伤。空腔流动及噪声产生的物理机制包含了4 个典型流动过程，即剪切层对涡扰动的放大、涡–腔体相互作用下压力波的产生、声波向上游逆向传播以及上游腔体边缘对声波的感受性增大导致的压力波向涡的转换。空腔几何特征对边界层分离和再附特性影响显著，并与流致噪声的产生和演化特点密切相关。一般而言，当腔体长深比小于10 时为开式空腔流动，此时剪切层跨过空腔开口区域并再附于空腔后壁及下游区域；当长深比大于13 时为闭式空腔流动，此时边界层在空腔前缘分离后再附于腔体底面；当长深比在10～13 之间时为过渡区域。Crook 等研究了三维空腔流动的基本特性，发现流向涡对流动稳定性影响显著，改变了空腔流场自持振荡特性。Liu 等通过连续时间压力场测量研究了剪切层中的多尺度旋涡与腔体壁面的相互耦合作用，发现剪切层内的低频运动对空腔流动的自持振荡有显著影响。Tuerke 等采用稳定性分析理论研究了不可压缩腔体内由反射波导致的声振频率选择特性。Sarohia和Tam 等基于扰动反馈机制建立或改进了空腔振荡频率半经验预估模型，改进了预测结果与风洞试验结果的符合度。

近年来，面向未来先进飞行器弹舱应用的广阔前景，杨党国等提出了一种典型结构的平板–空腔标模（C201）参数选择和设计方案，利用理论分析、数值模拟和风洞试验对空腔气动特性和噪声载荷进行了研究，得到了不同马赫数和迎角下C201 空腔标模的气动特性，采用前缘锯齿/直板/圆柱等扰流装置对空腔噪声抑制效果进行了分析，为相关研究提供了基本验证数据和借鉴。与此同时，利用机器学习方法辅助流场测量、预测及控制的研究如火如荼。为降低喷气式飞机噪声对飞行甲板人员健康及安全的危害，Tenney 等利用描述超声速情况下复杂非轴对称射流近场和远场条件的数据库，建立深度学习网络，正确识别了峰值辐射方向，并准确表示了远场噪声方向性趋势。由此可见，在大数据时代，机器学习为多元非线性回归问题提供了强有力的技术支撑。

此外，针对深度神经网络容易过度拟合、预测泛性较差等问题，研究者提出了多种改善策略。例如，利用元搜索、随机搜索、贝叶斯优化等方法构建神经网络结构，增强网络非线性映射的学习能力；通过自动编码器、卷积神经网络等新型神经网络模型提取流场特征，直接学习输入流场特征与预测物理量之间深层次的映射关系，针对时间依赖问题，Vlachas 等利用长短记忆神经网络训练学习时间序列数据，在混沌动力学系统和高原气候模型应用中取得良好效果。训练前对数据进行降阶、归一等预处理，以及训练过程中融入特定流动问题的预先知识、经验和控制方程，都能够抑制神经网络过度拟合，提高预测精度和自适应性。Pawar 等采用离线、在线的策略，对复杂流体流动非侵入式模型降阶，利用神经网络学习、预测受热腔体流的流场特性；对于样本外的较高瑞利数情况，能够预测瞬时温度场和时均努塞尔数，且具备令人满意的精度。神经网络过度拟合问题的逐步改善以及预测性能的提升，为指导设计、优化流动控制问题提供了一定的性能保障和技术参考。

因此，为探索人工智能和机器学习应用于多参数影响下空腔气动/声学特性预测的可能性，以及获得空腔噪声智能化控制参数优化设计的可行性，本文在前期工作基础上，进一步开展C201 空腔标模气动特性数值计算和前缘锯齿噪声控制试验研究，形成了多参数下空腔噪声载荷数据库，应用基于数据驱动的人工智能方法，建立智能化空腔气动特性预测模型和噪声控制模型，实现空腔内部气动特性智能化分析，形成前缘锯齿降噪智能优化设计方案。

1 研究模型和方法

为建立空腔气动/声学特性智能化预测模型和噪声控制智能模型，首先对C201 空腔标模（如图1所示）进行了高速补充试验，获得了试验马赫数0.6、0.9、1.5 和2.0 下完整的空腔气动特性和噪声数据库；然后，开展了前缘锯齿被动噪声控制试验，试验马赫数为0.9 和1.5；最后，基于试验数据建立了深度神经网络智能预测模型。试验在中国空气动力研究与发展中心0.6 m 跨超声速风洞中进行。该风洞为半回流暂冲式风洞，试验段截面尺寸0.6 m×0.6 m，试验段长度1.775 m，试验马赫数0.4～3.0。

图1 C201 空腔标模[23]Fig.1 C201 cavity model[23]

1.1 C201 空腔标模风洞试验

平板–空腔试验模型的结构如图1所示。为使湍流边界层充分发展，空腔前设置一块长约200 mm的平板。空腔长度L=200 mm，深度D=33.33 mm，宽度W=66.67 mm。

与其他常规试验相同，空腔模型的静压测点、脉动压力测点交替分布于空腔模型的前缘侧壁和底面，如图2所示。一共布置9 个静压测点和8 个脉动压力测点。其中，前缘侧壁布置1 个静压测点和1 个脉动压力测点，其余测点沿底面中轴线均匀分布，静压测点和脉动压力测点的间隔为28 mm。

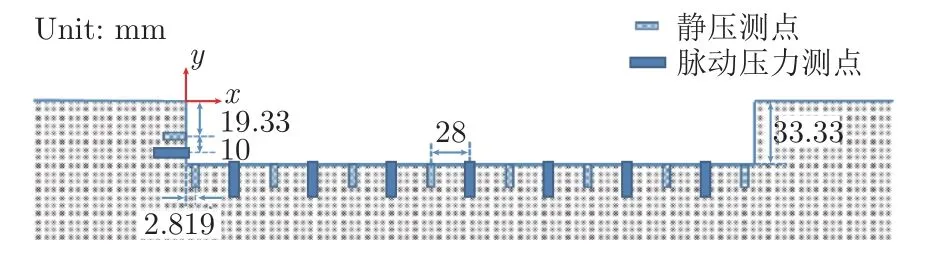
图2 空腔底部对称线上的静压和脉动压力测点Fig.2 Static and fluctuate pressure measurement points

在来流马赫数0.6、0.9、1.5 和2.0 条件下，采集空腔模型在迎角-6°、-4°、-2°、0°和2°时的静压和脉动压力数据。为描述空腔内噪声分布情况，以声压级L反映腔内流场的脉动压强。声压级可通过脉动压力测点采集的时域交流信号p（t）求得：

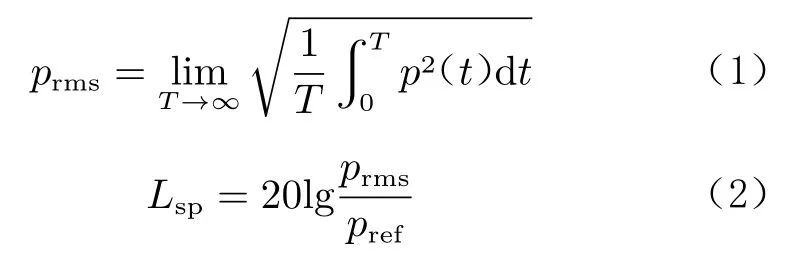
式中，p为脉动压力均方根值，T 为样本长度，参考压力p= 2×10Pa。

1.2 前缘锯齿噪声控制试验

通过在空腔前缘设置前缘锯齿的方式，改变来流边界层形态，进而达到控制流动噪声的目的。前缘锯齿布置位置及几何外形如图3所示。针对底高h、齿高e 和齿角这3 个参数，优化前缘锯齿几何外形。前缘锯齿挡板与水平方向的夹角为。前缘锯齿流动控制试验的脉动压力测点数目和分布位置与空腔模型相同。试验共设置由14 组不同几何外形控制参数（如表1所示）确定的前缘锯齿流动控制装置。各装置分别在来流马赫数为0.9 和1.5 的情形下，采集迎角为-6°、-4°、-2°、0°和2°时的腔内脉动压力时域信号。经数据后处理可获得声压级在各测点的分布情况。通过调整不同的h、e、和，研究这些参数对空腔底部声压级的影响，建立相应数据库，为建立空腔噪声智能控制预测模型奠定基础。

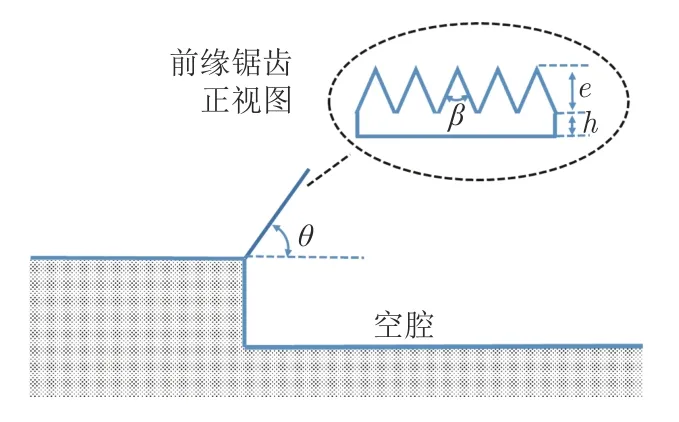
图3 前缘锯齿流动控制Fig.3 Leading-edge serrations for flow control

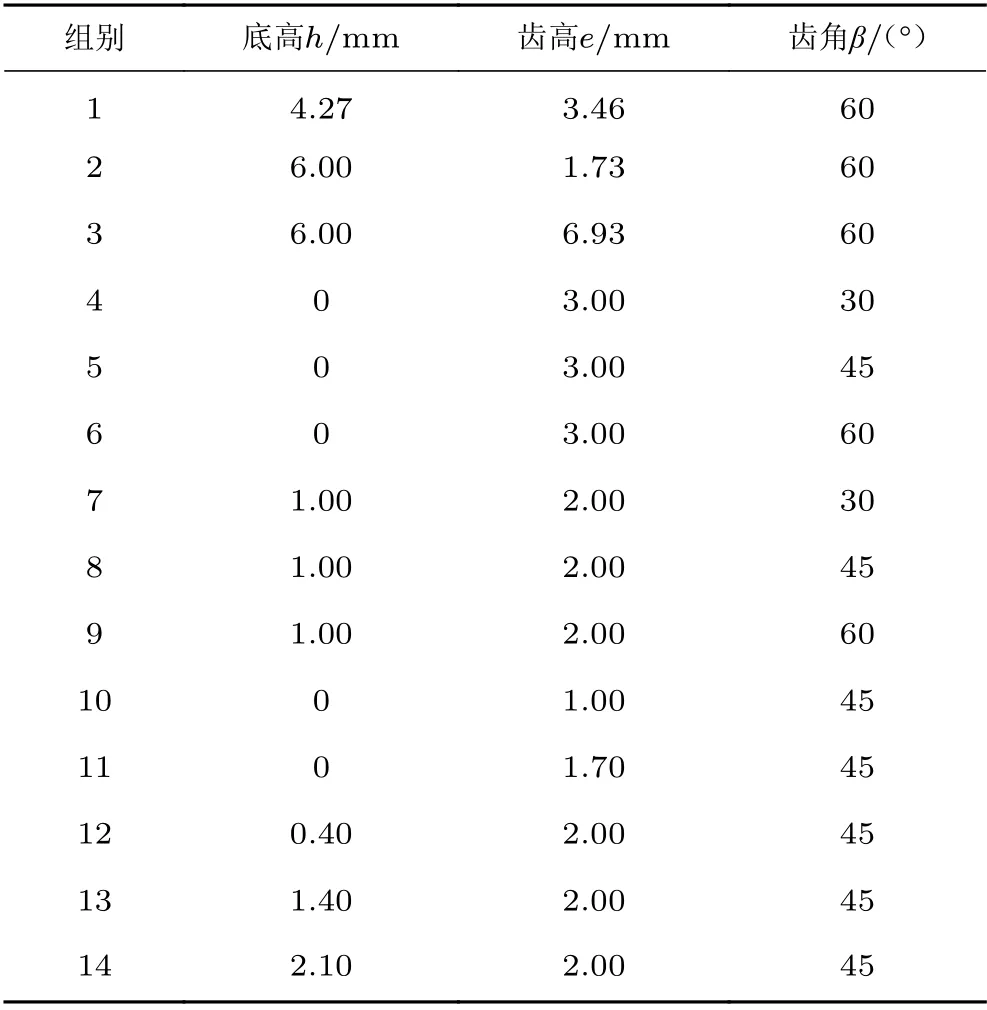
表1 不同前缘锯齿流动控制装置几何参数Table 1 Different geometric parameters of the leading-edge serrations for flow control

1.3 气动特性预测深度神经网络模型

通过C201 空腔标模高速流动试验及其前缘锯齿被动噪声控制试验，获得了不同马赫数、迎角、锯齿形状等多参数下空腔底部对称线上的静压、脉动压力和频谱特性等大量数据。这些数据实际上隐含着空腔流动和噪声载荷分布特征。基于数据驱动的深度学习方法采用多层人工神经网格（图4）在多个数据/信息处理层自动学习，建立多输入–多输出神经网络来表征任意复杂函数关系，就能够找到数据的特征关系。基于马赫数0.6～2.0 空腔流动试验数据和前缘锯齿被动噪声控制试验数据，应用深度神经网络算法，分别建立智能化气动载荷预测模型和噪声控制智能模型，实现空腔内部载荷的智能化分析和前缘锯齿形状的优化设计。

图4 多输入-多输出的深度人工神经网络模型Fig.4 Deep artificial neural network with multiple inputs and outputs

对于空腔标模流动试验，选取马赫数Ma 和迎角作为输入参数，不同位置上的静压和声压级作为输出参数，建立深度人工神经网络模型，其输入–输出关系可以表示为：

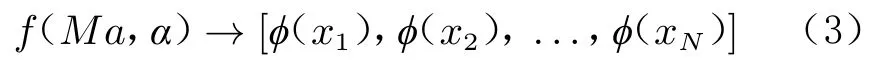
式中，函数f 表示输入–输出之间的映射关系，（x）表示腔体底部坐标为x位置上的静压或声压级，N 为测点位置总数。需要注意的是，这里没有采用传统的多输入–单输出的函数关系，避免了在不同位置上重复训练模型，使得学习过程更加简便，得到的最终模型可一次性输出所有位置上的静压或声压级，实用性更强。

对于前缘锯齿被动噪声控制试验，在固定的马赫数下，以锯齿几何参数和迎角作为输入，不同位置上的声压级作为输出，建立前缘锯齿被动噪声控制的深度神经网格模型，输入–输出关系为：

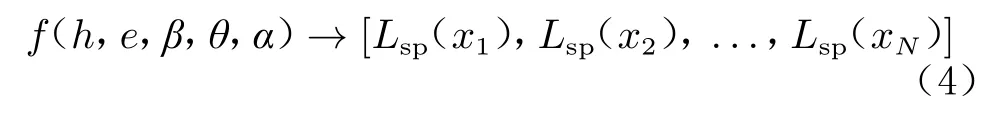
式中，函数f 表示输入–输出之间的映射关系，（x）表示腔体底部坐标为x位置上的声压级。由于输入参数的多样性（包含了长度、角度等参数），数据值变化较大，故采用了归一化处理。

深度神经网络模型的预测性能不仅依赖于训练数据，还与模型本身若干参数的选取有着重要关系，如网络的深度n、每层神经元的个数n、正则化数、学习效率和迭代次数n。从这些参数组成的参数空间内选取一组合适的超参数，不仅极具挑战性，对最终模型的性能也有着重要影响。一般而言，与增加每个隐藏层的神经元数相比，适当增加神经网络的隐藏层数（即深度神经网络）更能增强网络预测的鲁棒性和广泛性。然而，针对不同的问题，神经网络的构造会有不同的形式。

目前，比较成熟的网络结构选取方法有人工搜索算法、网格搜索算法、随机搜索算法和贝叶斯优化等。大部分研究工作默认采用的人工搜索算法基于对神经网络的浅显认知和工程经验。当问题对神经网络的超参数并不敏感或研究重心并不侧重于网络构造时，神经网络的隐藏层数、神经元数等参数可采用人工搜索算法保守估计和调整。网格搜索算法在一定程度上缓解了网络构造对研究人员个人能力的要求。然而，当涉及高维参数空间时，网格搜索会陷入“维度诅咒”困境。针对这一问题，Smolyak 稀疏网格等数值技术通过在参数空间中构造插值或积分点对参数节点稀疏采样，从而减轻计算负担。结合统计概率理论，应用随机搜索算法对问题进一步解放，并将计算控制在可接受的成本范围内。随机搜索算法在参数空间内随机选择一组超参数，先利用试验数据进行完整的训练，然后利用损失函数估计模型性能，将在所有参数中损失函数最小者视为性能最优。该算法的效率和所建立的模型性能都高于人工搜索算法和网格搜索算法，因此采用该算法对智能模型的超参数进行选择。所选取的超参数范围如表2所示。

表2 深度神经网络模型超参数范围Table 2 Ranges of hyper-parameters in DNN model

最终训练所得的模型是参数空间内损失函数最小的一个。对于C201 空腔标模流动的静压和声压级智能预测模型以及前缘锯齿被动噪声控制模型，损失函数E 定义为：

即损失函数为试验数据和智能模型预测值的L2 范数。模型的训练过程如图5所示。

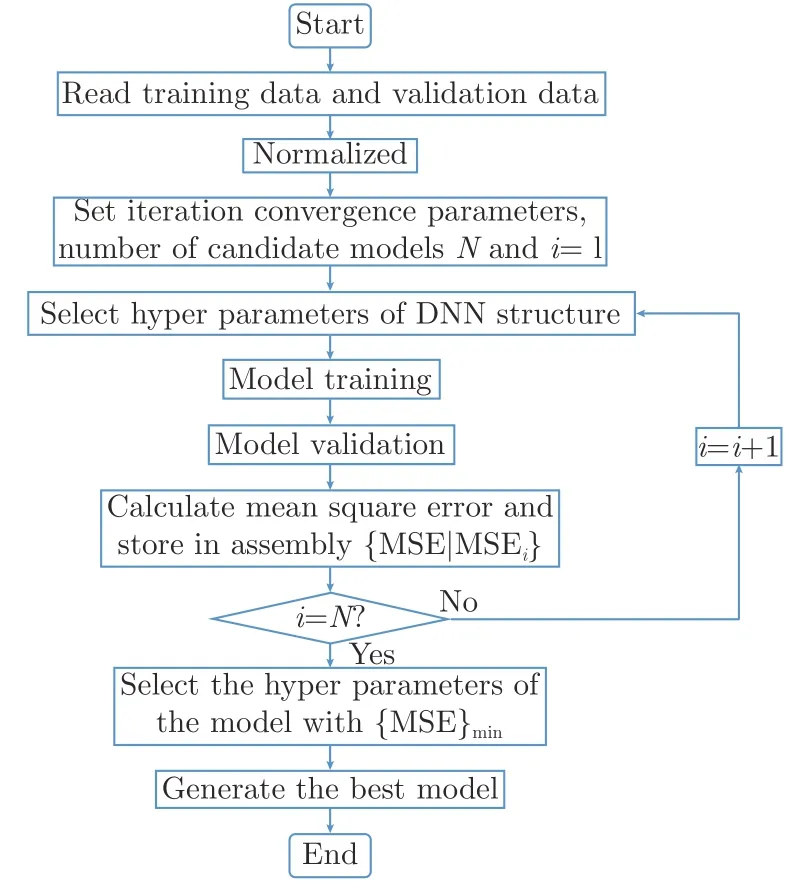
图5 空腔载荷智能模型算法训练流程Fig.5 Flowchart for the training of the deep forward neural network models for the prediction of cavity loads

2 气动特性智能预测结果分析

基于马赫数0.6～2.0、迎角-6°～2°条件下的C201 空腔标模试验所得到的静压、声压级以及频谱数据库，以马赫数和迎角为输入，不同测试点上的静压、声压级和频谱为输出，建立多层前馈神经网络模型，然后分别进行训练，最终得到静压、声压级和频谱预测的深度神经网络模型。下面对模型在训练集和测试集中的预测结果进行分析。

2.1 静压智能预测分析

建立静压智能预测模型所应用的训练集和测试集参数如表3所示。

表3 静压智能预测模型的训练集和测试集Table 3 Training and test sets for the prediction model of the static pressure coefficient

训练集含有19 组数据，测试集含有1 组数据。静压预测模型的训练过程遵循图5所展示的流程，训练好的深度神经网络模型具有7 层，各层的神经元数分别为2、41、43、25、13、19 和9。输入层有2 个神经元，用来表征马赫数和迎角；输出层9 个神经元，用来表征如图2所示的9 个静压测点上的压力系数。图6给出了静压系数C的损失函数随迭代次数变化的过程。随着迭代次数的增加，损失函数的变化逐渐趋于一个稳定的小量1.1×10，表明所训练的深度神经网络模型已经达到收敛。

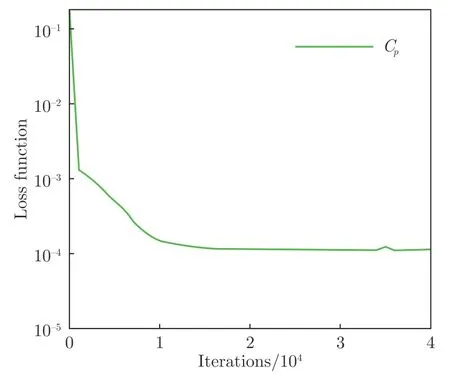
图6 损失函数随迭代次数的变化Fig.6 Evolution of the loss function with iteration number

图7给出了训练集内不同马赫数下迎角为0°和-6°时空腔底部对称线上的静压系数试验值与深度神经网络模型预测值的对比。在腔内前半部分，静压系数变化比较平稳，靠近后缘时剧增。在所考虑的来流条件下，静压系数随马赫数变化剧烈，但试验值和模型预测值始终符合良好。图8展示了测试集内空腔底部对称线上静压系数试验值与模型预测值的对比。无论训练集还是测试集，模型预测的静压系数最大误差都在1%以内。

图7 训练集内不同马赫数下空腔静压系数试验值与模型预测值对比Fig.7 Comparison of static pressure coefficients along the symmetric lines at the bottom of the cavity between the experimental data and the results predicted by the DNN model in the training data sets

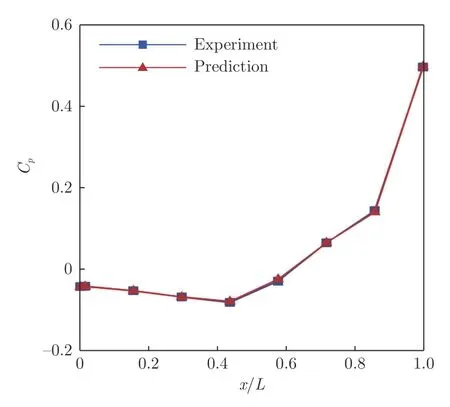
图8 测试集内空腔底部对称线上静压系数试验值与模型预测值对比Fig.8 Comparison of static pressure coefficients along the symmetric lines at the bottom of the cavity between the experimental data and the results predicted by the DNN model in the test data sets

2.2 噪声声压级智能预测分析

空腔内的流致噪声由压力脉动导致且随马赫数和迎角剧烈变化。不同空腔位置的噪声强度也不一样。建立空腔噪声声压级预测模型所采用的训练集和测试集的参数如表4所示。

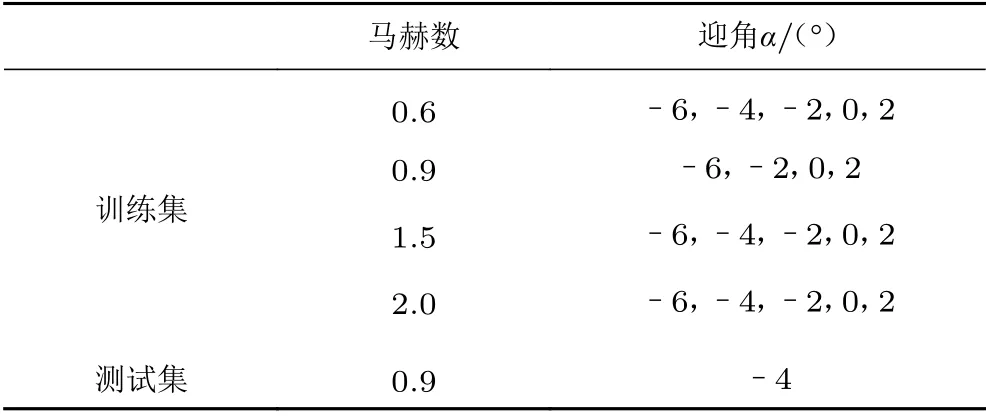
表4 声压级智能预测模型的训练集和测试集Table 4 Training and test sets for the prediction model of the sound pressure level

最终的深度神经网络模型共有6 层，各层的神经元数为2、34、20、26、14 和8。输入层有2 个神经元，用马赫数和迎角来表征影响空腔噪声特性的敏感参数；输出层有8 个神经元，用来表征如图2所示的8 个静压测点上的压强系数。图9对比了训练集内不同马赫数下空腔底部对称线上的声压级试验值与智能预测模型的预测值。可见，空腔内声压级随马赫数呈非线性变化，在马赫数1.5 时，声压级在腔内后缘达到了最大值，幅值超过了170 dB。图10 给出了测试集内的声压级对比，在腔内前半部分，声压级呈减小的趋势，靠近后缘时则逐渐增大。无论是在测试集内还是训练集内，收敛后的损失函数的相对误差均在10量级，空腔内各测点声压级的相对误差都在0.5%以内，这表明所得的智能预测模型能够精确预测不同马赫数和迎角下的噪声在空腔内的分布情况。

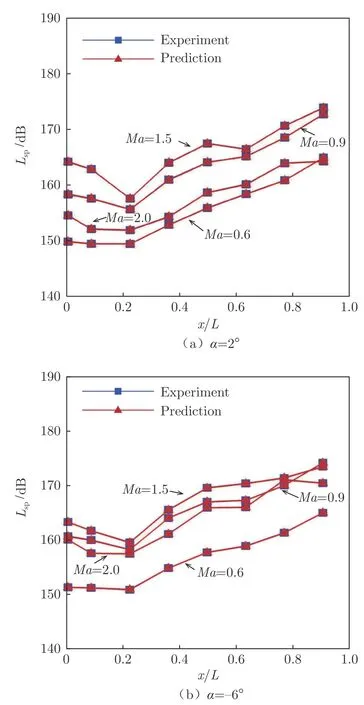
图9 训练集内不同马赫数下空腔声压级试验值与模型预测值对比Fig.9 Comparison of SPL along the symmetric lines at the bottom of the cavity between the experimental data and the results predicted by the DNN model in the training data sets

图10 测试集内空腔声压级试验值与模型预测值对比Fig.10 Comparison of static pressure coefficients along the symmetric lines at the bottom of the cavity between the experimental data and the results predicted by the DNN model in the test data sets

2.3 噪声频谱智能预测分析

表5给出了建立腔内不同位置的频谱特征深度神经网络模型的训练集和测试集参数。模型的输入为马赫数、迎角和腔内位置，输出为不同频率下的声压幅值。对试验得到的压力脉动数据进行傅里叶变换，对表5所示的每个状态和8 个腔内脉动压力测点分别建立频率范围6～7 000 Hz 的1 252 个幅频点数据库。基于该数据库的数据基础，对神经网络模型进行集成训练，最终损失函数下降了超过4 个量级，其相对值（相对于最大幅值）小于0.5%，即模型在训练集内的预测误差不超过0.5%。所建立的深度神经网络模型架构含有5 层，各层的神经元数为3、25、40、47 和1 251。

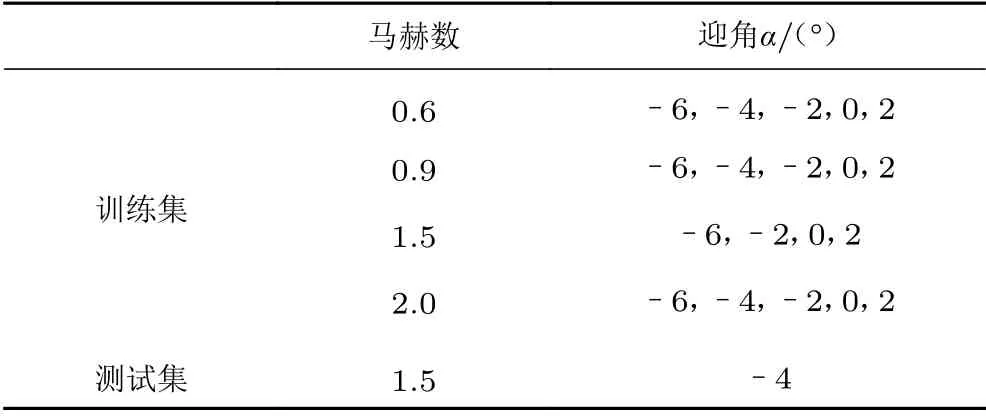
表5 频谱智能预测模型的训练集和测试集Table 5 Training and test sets for the prediction model of sound spectrum

图11 给出了训练集内马赫数0.6、迎角–4°下3 个不同位置上的气动噪声频率特性。从图中可以看出，所得到的模型对腔内噪声的幅频特征和前3 阶模态捕捉良好。随着位置后移，声压幅值在所有频段上整体抬高。图12 给出了测试集内马赫数1.5、迎角–4°下不同位置上的气动噪声频率特性。所得到的结果与试验值符合良好，且准确捕捉了最重要的前3 阶流激振荡声波模态信息，充分验证了本文所建立的深度神经网络频谱预测模型具有良好的预测能力。

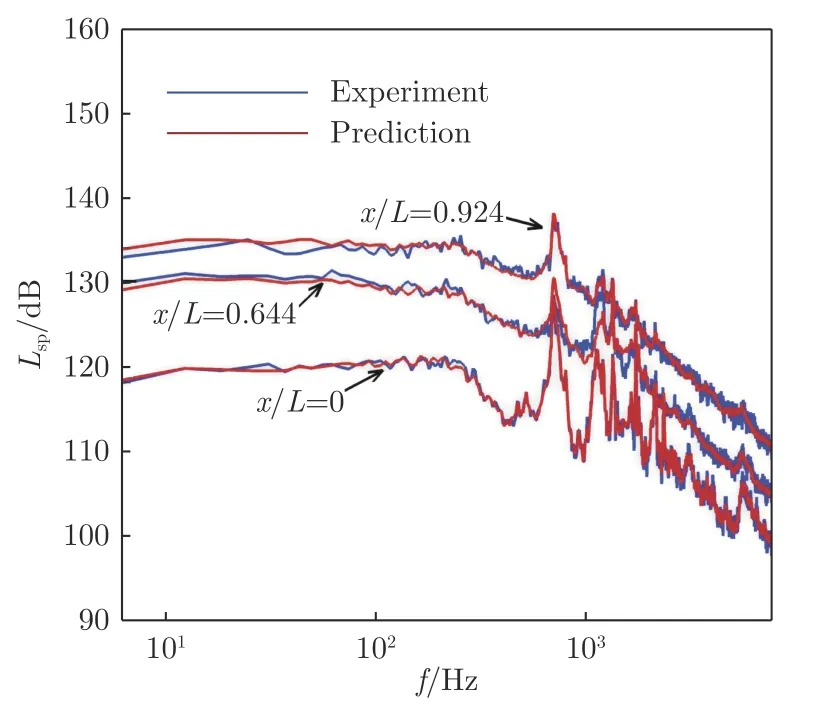
图11 马赫数0.6、迎角-4°时，训练集内不同位置上的噪声频率特性Fig.11 Comparison of spectrum at different positions of the cavity at Ma=0.6 and α=-4° between the experimental data and the results predicted by the DNN model in the training data sets

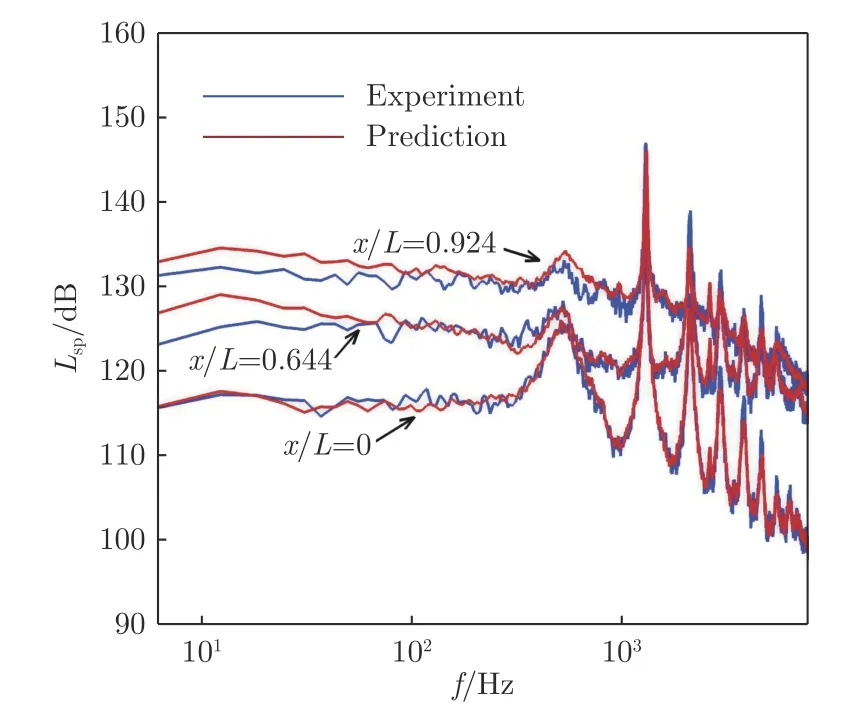
图12 马赫数1.5、迎角-4°时，测试集内不同位置上的噪声频率特性Fig.12 Comparison of spectrum at different positions of the cavity at Ma=0.6 and α=-4° between the experimental data and the results predicted by the DNN model in the test data sets

3 控制参数智能快速优化设计

试验结果表明：当Ma=1.5 时，腔内声压级在所有试验参数内最高。采用图3所示的前缘锯齿和表6和7 给出的参数，对腔内噪声进行控制试验，建立Ma1.5 时不同迎角下的声压级特性数据库，共计70 组数据。随机选取其中80%的数据为训练集，其余20%为测试集。选取前缘锯齿的3 个几何参数（底高、齿高和齿角）以及迎角作为输入，以腔内8 个不同脉动压力测点位置的声压级为输出，利用训练集的数据库对深度神经网络模型进行训练。建立了深度为4 层的神经网络模型，各层的神经元数为4、43、21 和8，损失函数（相对于声压级最大值）在10量级，表明模型已经收敛，且在训练集内预测的声压级相对误差在0.1%以下。

表6 前缘锯齿噪声控制试验参数及智能预测模型的训练集Table 6 Training sets for the prediction model of SPL with leadingedge serrations for noise control

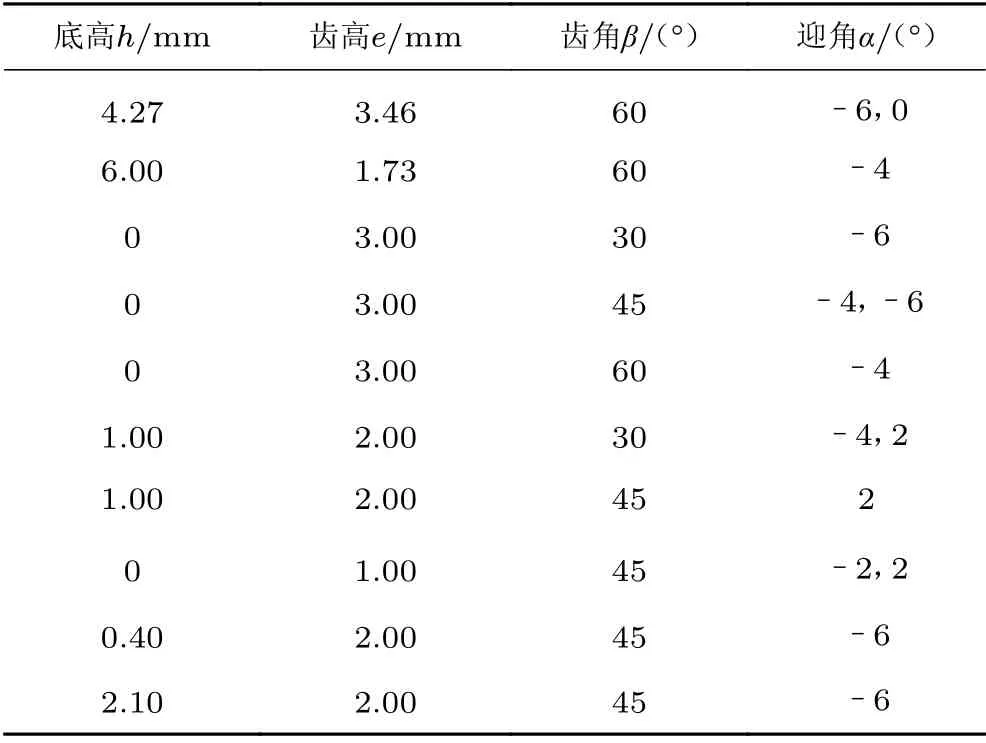
表7 前缘锯齿噪声控制试验参数及智能预测模型的测试集Table 7 Test sets for the prediction model of SPL with leading-edge serrations for noise control

图13 给出了Ma=1.5 时前缘锯齿噪声控制神经网络模型预测声压级和试验值的对比。其中，Case 1在训练集内（h=4.27 mm， e=3.46 mm，=60°，=2°），Case 2（h=1.00 mm，e=2.00 mm，=30°，=-4°）和Case 3（h=0 mm，e=1.00 mm，=45°，=2°）在测试集内。可以看到，所建立的前缘锯齿噪声控制神经网络智能模型具有良好的预测精度和广泛性，在训练集和测试集内都与试验获得的声压级分布情况吻合良好，可为后续优化前缘锯齿控制参数提供可靠的数值预测参考。

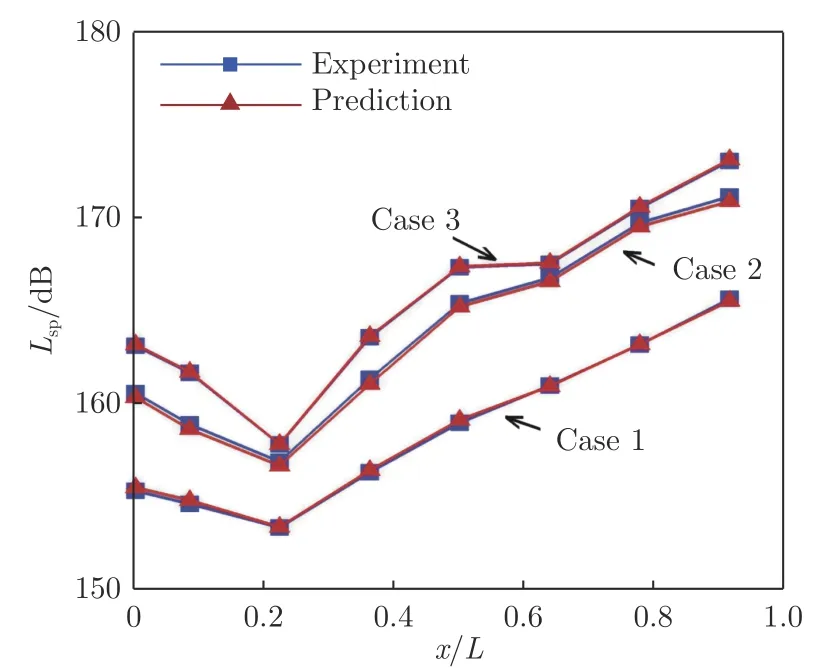
图13 Ma=1.5 时，前缘锯齿噪声控制神经网络模型预测声压级对比Fig.13 Comparison of SPL between the experimental data and the results predicted by the DNN model for cavity flows at Ma=1.5 with leading-edge serrations noise control

在试验数据库中，通过遍历搜索，发现= 0°时前缘锯齿噪声控制效果最好的一组锯齿参数为h=6.0、e=6.93 和=60°。应用前缘锯齿噪声控制神经网络智能模型，在前缘锯齿几何参数空间（底高h=0～6 mm，齿高e=1.00～6.93 mm，齿角=30°～60°）进行寻优搜索，通过循环得到声压级下降最大（即噪声控制效果最好）的几何参数，其参数为h=2.0、e=6.85 和=60°。图14 给出了当齿角固定为60°时的不同底高和齿高参数空间内的最大声压级降幅值。

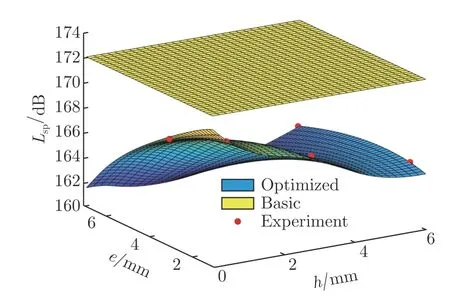
图14 齿角固定为60o 时不同底高和齿高参数空间内最大声压级降幅值Fig.14 Maximum decrease of SPL with different h and e

图15 给出了前缘锯齿参数优化前后的腔内声压级对比（Basic：无控制；Noise control：h6.0 mm，e6.93 mm，60°； Optimized noise control： h=2.0 mm，e=6.85 mm，=60°）。可以看到，优化后的锯齿能够降低的最大声压级为11.22 dB，比试验最优结果还降低了2.60 dB。

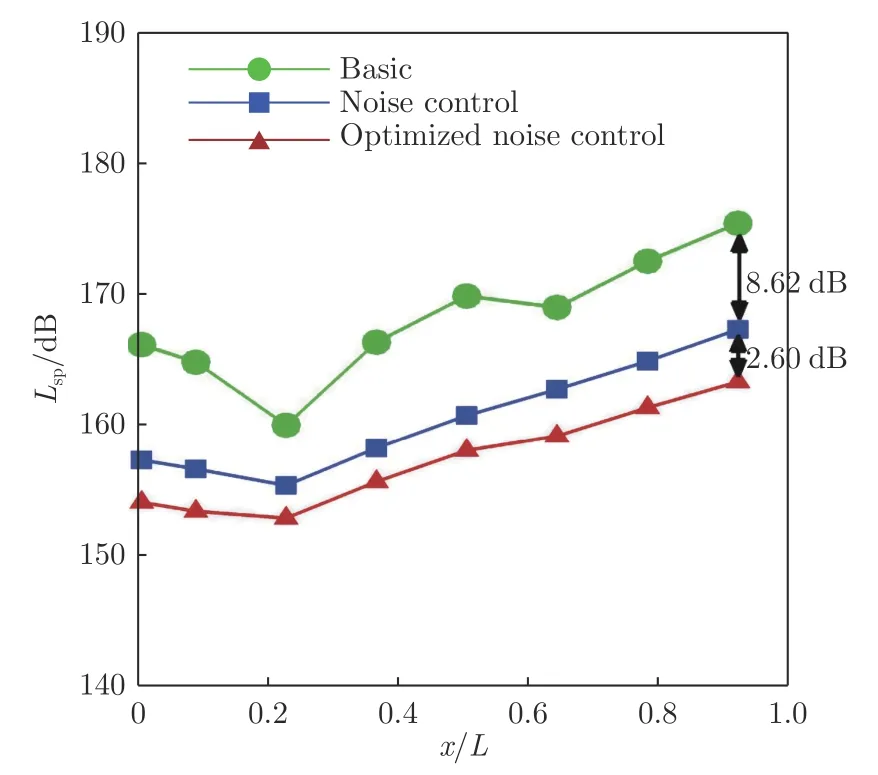
图15 前缘锯齿参数优化前后腔内声压级对比Fig.15 Comparison of SPL for cavity flows with original leading-edge serrations control and optimized serrations control

表8给出了不同迎角下前缘锯齿结构优化后的参数及噪声控制效果。可以看到，在迎角-6°～2°范围内，锯齿的几何参数在不同迎角下都具有较好的收敛性，优化后的前缘锯齿可以把腔内最大声压级降低10 dB 以上，且比优化前的锯齿控制参数下的最大声压级再降低了2.60 dB。

表8 不同迎角下前缘锯齿结构优化后的参数及其噪声控制效果Table 8 Optimized geometrical parameters for the leading-edge serrations and its noise control result

4 结 论

通过搜集整理马赫数0.6～2.0 和迎角-6°～2°条件下的飞行器典型空腔结构（C201）气动特性和噪声载荷测量试验数据，获得了腔内静压、声压级和噪声频谱特性的基本数据库；应用不同几何形状参数的前缘锯齿对腔内噪声进行了被动控制试验研究，构建了空腔气动特性和噪声载荷控制效果数据库。基于机器学习分别建立了空腔静压预测、声压级预测和噪声频谱预测的深度神经网络前馈模型，实现了有限约束条件下的空腔气动特性快速智能预测；构建了空腔模态声波数据模型，能够对空腔模态噪声分布进行智能分析。应用所建立的前缘锯齿空腔噪声控制神经网络模型，对锯齿几何参数进行了智能优化设计，参数优化后的锯齿可达到腔内最大声压级降低10 dB 以上的良好效果，为空腔噪声控制模型构建和参数智能优化提供了有效的解决途径。