高超声速风洞现代试验设计方法研究

2022-07-14尤文佳王慧杰韩仁坤陈刚

实验流体力学 2022年3期

关键词：拉丁风洞试验迎角

尤文佳，王慧杰,，韩仁坤，陈刚,*

1.西安交通大学航天航空学院机械结构强度与振动国家重点实验室，西安 710049

2.西安交通大学航天航空学院陕西省先进飞行器服役环境与控制重点实验室，西安 710049

3.中国航天科工集团第三研究院创新研究院，北京 100074

0 引言

高超声速飞行器具有高速度、强机动、超远程等特点，是当今世界航空航天强国研究的热点。由于高超声速飞行器在大气层内飞行时间长，飞行器气动力/热环境等非常严酷，给气动研究带来了巨大挑战。风洞试验在气动研究中发挥着重要的作用，在飞行器从初步设计到机型选择、定型、研制的各个阶段，总体、结构和控制等设计都需要大量的风洞试验数据提供支持。随着我国国防事业的发展，飞行器设计的战术技术指标要求不断提高，这意味着对风洞试验技术也有了更高的要求。对于风洞试验技术的研究，应朝着高精准度试验数据、低成本和短周期等方向发展。

目前，传统试验设计（OneFactoratATime，OFAT）方法是风洞试验设计采取的主要方法，即每次试验中只有一个变量（如迎角）发生变化，其他变量保持不变，获取响应变量（如气动系数）的结果，进而得到响应变量的变化规律。该方法作为一种基于大量试验数据的方法，需要进行大量的风洞试验。

近年来，现代试验设计（Modern DesignofExperiments，MDOE）方法已经广泛应用于航空航天、交通运输、农业、生物、医学等领域，在大型设备、工况复杂、耗能高等试验的优化设计中取得了良好的社会经济效益。MDOE 方法结合优化设计、数理统计等设计试验，通过少量的试验即可得到更优的试验结果、建立精度较高的模型。MDOE 方法的目的已经不是简单地获取大量“数据”，而是获取数据中蕴含的“知识”。

1997年，美国航空航天局（NASA）兰利研究中心首次提出使用MDOE 方法取代传统的OFAT 方法，目前已经成功应用于多项型号风洞试验。2011年，DeLoach 等开展了以导弹为研究对象的MDOE 方法应用研究，并与传统的OFAT 方法对比，将试验次数减少了80%。近些年，国内针对MDOE 方法在风洞试验中的应用展开了研究，但仍比较欠缺。李国帅等采用区组化的回归方法设计试验并获取数据，建立了二阶响应面模型，使样本点减少了80%左右。张江等采用IV–最优设计获取样本点进行试验，使样本点减少了46%，并发现MDOE 方法与OFAT 方法获得的气动系数相差不大。张江等随后又开展了MDOE 形式的试验设计方法研究，运用空间填充设计（而非以往的经典试验设计）可使试验样本点减少33.3%。李多等将MDOE 方法应用于2.4 m 跨声速风洞试验，采用分区间的中心复合设计，所需样本点仅为OFAT 方法的20%左右。

在国内外公开发表的研究中，MDOE 方法主要应用于二变量（如迎角+侧滑角）试验，对三及三以上变量（如迎角+侧滑角+舵偏角）的风洞试验设计还较少。在实际工程应用中，不同舵偏角情况下的三及三以上变量的风洞试验大量存在，但很多风洞模型在改变舵偏角时难以做到像二变量试验中改变迎角和侧滑角那样全自动化。因此，在现有风洞控制系统下，采用OFAT 方法的三及三以上变量试验的效率会更低。对于不具备自动调节舵偏角的风洞试验模型而言，适用于三及三以上变量试验的MDOE 方法就显得尤为重要。

大部分二变量试验设计采用经典拉丁超立方方法，样本点在二维各方向上都随机分布。虽然该方法的样本点数量比OFAT 方法明显减少，但现有风洞控制系统迎角和侧滑角可以连续变化，因此理论上该方法不会大幅度提高试验效率。同样，在三变量试验中，样本点在三维各方向上随机分布，在不具备自动调节舵偏角的风洞模型中，加大了试验走刀顺序的不便性。因此，在经典拉丁超立方方法基础上，发展一种能够尽量结合现有风洞控制系统特点，又能显著提高实际试验效率的MDOE 方法具有重要意义。

针对当前多变量风洞试验设计面临的问题，本文发展一种基于分层拉丁超立方的现代风洞试验设计方法，并将该方法运用于高超声速风洞（马赫数6）试验模型，从风洞试验数据库中获得气动数据结果，并对该方法进行验证。

1 MDOE 方法

本节主要介绍MDOE 方法涉及的相关理论，包括确定样本点的分布及数量、构建响应模型。

试验选择迎角、侧滑角和舵偏角作为设计变量，气动系数作为因变量。为避免数学模型中出现高阶项，引入分区间设计技术，将迎角区间划分为小迎角区间和大迎角区间，分别进行试验设计。

1.1 确定样本点

目前，拉丁超立方设计（Latin Hypercube Sampling，LHS）是MDOE 研究中采用的方法之一，属于空间填充设计，在解决非线性问题时具有较大的优势，多适用于设计变量维度较高的情况，可使试验次数明显减少，试验次数与设计变量的水平数相同。

拉丁超立方设计将每个设计变量的定义域区间划分成个相等的小区间，共有个设计变量，这样整个数据空间被分成q个相同的小区域，最后选取个样本点。

选取样本点时，需遵循2 个原则：1）在每个小区域中，进行随机采样；2）在每一维变量上的每个小区间上只产生一个样本点，即样本点投影在每一维变量的方向上有个样本点。

对于多变量风洞试验，直接采用经典拉丁超立方设计的效果并不理想，实际操作中也不便于风洞试验点数据采集。因此，本文在经典拉丁超立方设计的基础上，提出了分层拉丁超立方设计方法。

分层拉丁超立方设计是指先将分层变量在其一维方向的定义域内均匀分层，假设均匀分为层，即有个水平值；再将剩余的设计变量进行拉丁超立方设计，将定义域区间划分成（一般）个相等的小区间。在样本点的分布上，分层拉丁超立方设计与经典拉丁超立方设计的不同点在于：样本点投影在分层变量的方向上有个样本点，都在其水平值上；除分层变量外，样本点投影在其他每一维变量的方向上都有个样本点，且每个样本点都在其划分的小区间内。样本点数量与除分层变量外的其他变量水平数相同，即个样本点。例如，二变量试验中取迎角和侧滑角为设计变量时，选用迎角方向进行均匀分层，在侧滑角方向进行拉丁超立方设计；三变量试验中取迎角、侧滑角和舵偏角为设计变量时，选舵偏角方向进行均匀分层，在其他2 个方向进行拉丁超立方设计。

采用分层拉丁超立方设计方法，可得到迎角、侧滑角以及舵偏角组合状态下的样本点。分层拉丁超立方设计相比于经典拉丁超立方设计，可减少试验车次，提高试验效率，缩短试验周期。

1.2 样本点数量

响应面模型的阶次和试验精度决定了样本点的数量。在每个子迎角区间中，构建多项式响应面模型所需要的样本点数量不能少于此多项式的项数，最小样本点数量通过下式计算：

式中，为多项式项数，为多项式阶次，为多项式元数。

在二和三变量试验中，均采用三阶多项式模型：=2，=3，=10，最小数据量为10；=3，=3，=20，最小数据量为20。由于多项式响应面模型中存在对模型精度影响较大的点，这些点会引起“杠杆效应”，放大整个模型的误差，因此有必要增加一定量的重复点改善杠杆效应。为保证响应面预测值在平均95%置信概率水平下与设计空间中任一点的真实结果不出现显著差异，样本点数量需要满足：

在本文涉及的试验中，一个二维子数据空间只要达到17 个（=162510=1625）、一个三维子数据空间只要达到33 个（=162520=325）便可以使预测值落在95%置信区间内。在下文的二变量试验中，MDOE 方法的样本点为17 个；三变量试验中， MDOE 方法的样本点在舵偏角方向取5 层，每层17 个，共85 个。

为了进行MDOE 方法与OFAT 方法结果的对比，表1中给出了二变量试验中OFAT 方法所取的变量及水平值，小迎角区间取91 个点，大迎角区间取84 个点，是MDOE 方法的5 倍左右。

表1 二变量试验中OFAT 方法所取的变量及水平值Table 1 Variables and level values taken by OFAT method in the two-variable test

表2中给出了三变量试验中OFAT 方法所取的变量以及水平值。小迎角区间取245 个点，大迎角区间取294 个点，是MDOE 方法的3～4 倍左右。

表2 三变量试验中OFAT 方法所取的变量及水平值Table 2 Variables and level values taken by OFAT method in the three-variable test

1.3 响应面模型

多项式响应面模型在MDOE 方法中应用广泛，具有建模容易、计算量较小、预测较准的优点，可运用于工程试验设计的近似处理。本文的二变量试验和三变量试验均采用三阶模型，避免了高阶多项式表达式复杂、求解困难等问题。三阶模型的表达式为：

式中：为设计变量的响应函数，、c、c、c、c、c、c为多项式的待定系数，x表示第个自变量，表示变量个数。

2 分层拉丁超立方设计准则研究

拉丁超立方设计过程中会在每个小空间随机采样，容易出现分布不均匀的情况。为减少这种情况的发生，通常添加最大化最小距离、最小化最大距离、最小差异、相对理想累积分布最小均方根差异和相对理想累积分布最小最大差异这5 种准则促进其均匀性。最大化最小距离准则是使各样本点之间的最小距离最大化，最小化最大距离准则是使各样本点之间的最大距离最小化，最小差异准则是使偏离平均点密度的偏差最小化，相对理想累积分布最小均方根差异准则是使累积分布函数的均方差最小，相对理想累积分布最小最大差异准则是使累积分布函数的最大方差最小化。本节研究基于以上5 种准则的分层拉丁超立方设计方法，对比各准则效果。

一般情况下，针对横向气动系数的响应面模型的非线性程度较强。若样本点可以保证构建横向气动系数响应面模型，那么纵向一般也能保证。在小迎角区间（–2°～10°）开展基于不同准则的分层拉丁超立方方法的试验设计，并构建滚转力矩系数C的响应面模型，进行95%置信区间分析，结果如图1～5 所示。对于图1～5：图（a）中不同准则下的样本点为17 个，红色代表了重复点（共5 个）；图（b）中的滚转力矩系数响应面模型均为三阶模型；为了验证模型的有效性，在每个子区间选取=0 和=4时的6 或7 个OFAT 试验点，验证其是否可以落在拟合曲线的95%置信区间内，从图（c）和图（d）中可以看出，检验点均落在了置信区间内。置信区间的带宽是整体均方根误差平均值的2 倍。

图1 最大化最小距离准则的分层LHS 设计Fig.1 Stratified LHS design of maximum and minimum distance

图2 最小化最大距离准则的分层LHS 设计Fig.2 Stratified LHS design of minimum and maximum distance

图3 最小差异准则的分层LHS 设计Fig.3 Stratified LHS design of minimize discrepancy

表3中给出了不同方法的滚转力矩系数响应面均方误差、整体均方根误差和判定系数。整体均方根误差越小，判定系数越接近1，表明多项式模型的拟合效果越好。根据表3中的整体均方根误差以及判定系数可知，基于最大化最小距离准则的分层拉丁超立方设计效果最好。因此，在本文的应用示例中，采用最大化最小距离准则的分层拉丁超立方设计方法进行研究。

表3 不同准则下的响应面检验结果Table 3 Response surface test results of different criteria

图4 相对理想累积分布最小均方根差异准则的分层LHS 设计Fig.4 Stratified LHS design to minimize RMS variation from cumulative distribution function

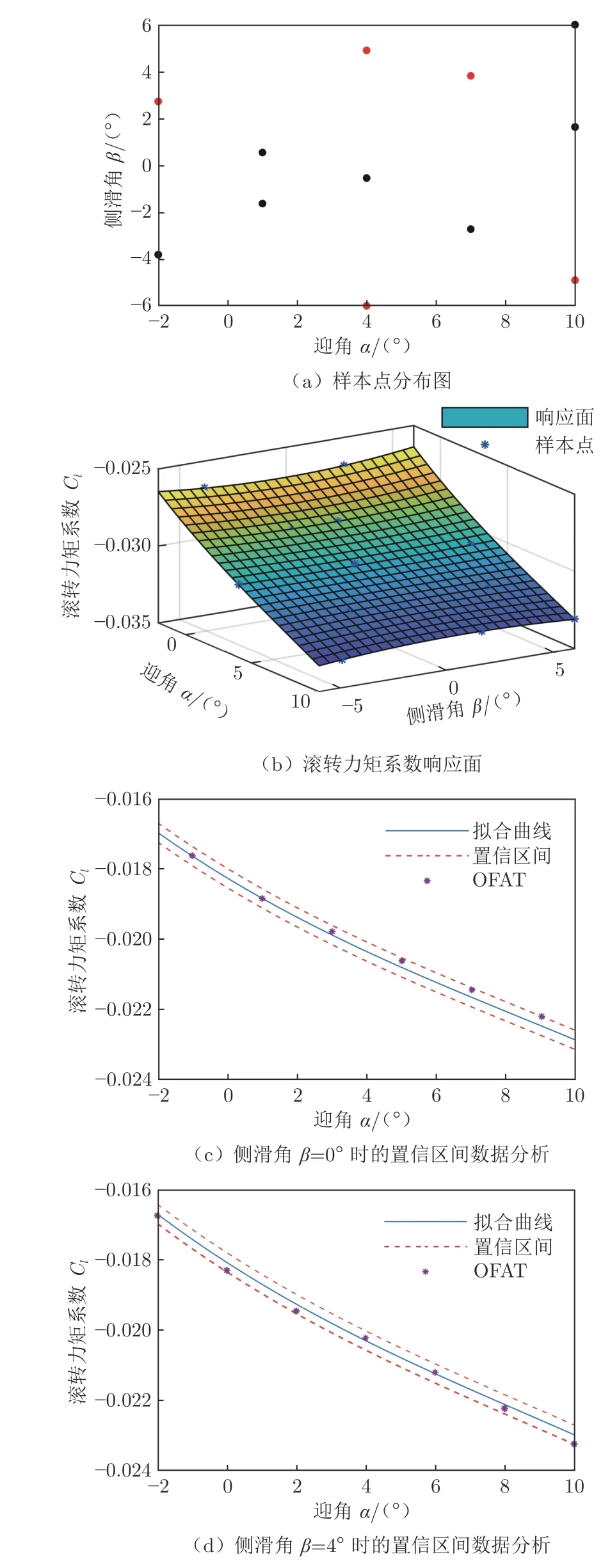
图5 相对理想累积分布最小最大差异准则的分层LHS 设计Fig.5 Stratified LHS design to minimize maximum variation from cumulative distribution function

3 二变量风洞试验设计验证

本节将基于最大化最小距离准则的分层拉丁超立方方法应用于二变量风洞试验，验证分层拉丁超立方风洞试验设计方法的可行性和有效性。采用某标准高超声速模型（舵偏角2.5°）在马赫数6 风洞中的试验数据进行设计方法验证，设计变量为迎角、侧滑角。

3.1 小迎角区间

变量取值：迎角=2～10；侧滑角=6～6。

因变量为纵向气动系数，包含升力系数C、阻力系数C和俯仰力矩系数C。在多项式响应面模型中，采取逐步回归的方法简化模型。图6（a）给出了样本点分布，数量为17 个，红色为重复点（共5 个）。从图6（b）中可以明显看出升力系数基本不受侧滑角的影响；迎角为主要影响因素，在迎角2°～ 8°之间升力系数呈现下降趋势。图6（c）中阻力系数随迎角的增大而增大。在图6（d）中，迎角越大，侧滑角越小，俯仰力矩系数越大。这体现了MDOE 方法的优势：可分析多变量对气动系数的影响。

图6 小迎角区间二变量试验的样本点分布及各纵向气动系数的响应面Fig.6 Sample point and response surface of each longitudinal aerodynamic coefficient for the two-variable test in small angle of attack

表4中给出了采用逐步回归方法确定的小迎角区间各纵向气动系数的响应面模型应含有的项，剔除了一些影响因素较小的不显著项。

表4 小迎角区间响应面多项式的构成Table 4 The formation of polynomials of response surface in small angle of attack interval

3.2 大迎角区间

大迎角区间仅迎角取值范围（= 10～25）与小迎角区间不同，侧滑角取值范围、因变量和样本点数量等都与小迎角区间相同。

图7（a）为大迎角区间的样本点分布；从图7（b）中可以明显看出，升力系数不受侧滑角的影响，迎角为主要影响因素，升力系数随迎角的增大而增大；在图7（c）中，迎角越小，侧滑角越大，阻力系数越小；在图7（d）中，迎角越大，侧滑角越小，俯仰力矩系数越大。

图7 大迎角区间二变量试验的样本点分布及各纵向气动系数的响应面Fig.7 Sample point and response surface of each longitudinal aerodynamic coefficient for the two-variable test in big angle of attack

表5中同样给出了采用逐步回归方法确定的大迎角区间各纵向气动系数的响应面模型应含有的项，即主要影响因素的构成。

表5 大迎角区间响应面多项式的构成Table 5 The formation of polynomials of response surface in big angle of attack interval

3.3 模型验证

为了验证模型的有效性，在侧滑角=0的截面上截取剖面线，选取6 个OFAT 试验点检验其是否落在95%置信区间内，置信区间的带宽与第2 节中的计算方法一样，结果如图8所示。在小迎角区间中，升力系数基本都能落在置信区间内，在阻力系数和俯仰力矩系数置信区间中，非线性强的区域（如迎角为2°时）升力系数落在置信区间上下限附近；在大迎角区间中，置信区间带宽较窄，检验点基本都能够落在上下限附近，说明响应面模型满足精度。

图8 各纵向气动系数的置信区间Fig.8 Confidence intervals of longitudinal aerodynamic coefficients

4 三变量风洞试验设计验证

本节采用某标准高超声速模型在马赫数6 风洞中的试验数据对比不同三变量风洞试验设计方法在大、小迎角区间的风洞试验结果。在此基础上，再将三变量分层拉丁超立方试验设计所得模型指定剖面预测值与二变量试验设计模型预测值进行对比，进一步验证所发展的三变量分层拉丁超立方试验设计的有效性。

4.1 小迎角区间

变量取值：迎角=2～10；侧滑角=6～6；舵偏角=75～75。

因变量为纵向气动系数，包含升力系数C、阻力系数C和俯仰力矩系数C。下面仅以俯仰力矩系数为例展示。分层拉丁超立方设计方法的样本点在舵偏角方向每层取为17 个（含5 个重复点），共5 层、85 个点，如图9（a）所示，红色为重复点。为更好地反映出多变量间复杂的耦合关系，采用3 个设计变量两两耦合的方式给出响应面图，将OFAT 方法获得的数据构建的标准响应面与拉丁超立方设计的响应面、分层拉丁超立方设计的响应面进行对比，其中拉丁超立方设计方法也是取85 个点。在俯仰力矩系数的响应面中，图9（b）中的LHS 响应面比分层LHS 响应面的误差更大；在图9（c）中的边界处，分层LHS 设计的响应面优于LHS 设计的效果；在图9（d）中，各方法吻合度较高，区别不明显。

图9 小迎角区间三变量试验俯仰力矩系数样本点分布及响应面Fig.9 Sample point and response surface of pitching moment coefficient for the three-variable test in small angle of attack

小迎角区间中，采用拉丁超立方方法时的整体均方根误差为0.014 8，而分层拉丁超立方方法的整体均方根误差为0.012 6。整体均方根误差越小，拟合精度越好，因此，分层拉丁超立方方法的拟合精度比拉丁超立方方法有一定的改善。

4.2 大迎角区间

大迎角区间仅迎角取值范围（= 10～25）与小迎角区间不同，侧滑角取值范围、舵偏角取值范围、因变量和样本点数量等都与小迎角区间相同。

图10（a）为大迎角区间三变量试验样本点分布。大迎角区间的俯仰力矩系数响应面如图10（b）～（d）所示。在图10（b）的迎角剖面中，LHS 设计和分层LHS 设计的响应面与标准响应面相比，在边界和边角处误差较大，中部区域拟合相对较好。在图10（c）和（d）的侧滑角剖面和舵偏角剖面中，3 种方法的效果相差不大，吻合度高。

图10 大迎角区间三变量试验俯仰力矩系数样本点分布及响应面Fig.10 Sample point and response surface of pitching moment coefficient for the three-variable test in big angle of attack

大迎角区间中，采用拉丁超立方方法时的整体均方根误差为0.007 5，而分层拉丁超立方方法的整体均方根误差为0.006 3。因此，分层拉丁超立方方法的拟合精度相比拉丁超立方方法有一定的改善。

4.3 三变量试验模型预测精度验证

为验证三变量试验模型的预测精度，在三变量试验获得的气动数据模型中，选取=25时的舵偏角剖面与第3 节中二变量试验所得的响应面进行相同变量条件下的纵向气动系数对比，如图11 所示。图中的结果总体吻合度较好，在边界处（非线性强的区域）以及边角处存在偏差。例如在图11（a）小迎角区间的升力系数响应面中，在侧滑角小于–5°时（非线性强的区域），边界和边角处的偏差较大。