超高速碰撞碎片云质量分布快速预测技术

周浩，李毅，兰胜威，刘海

中国空气动力研究与发展中心 超高速空气动力研究所，绵阳 621000

0 引 言

人类航天活动日趋频繁，空间碎片数量急剧增加，对航天器构成了严重威胁。目前，以国际空间站为代表的长期在轨航天器一般采用Whipple 防护屏技术进行空间碎片防护，基本思想是在航天器舱壁前一定距离处设置一薄板，在空间碎片（下文统称为弹丸）超高速碰撞（Hypervelocity Impact，HVI）下形成碎片云，使入射弹丸动能被高度分散，从而实现对航天器的有效保护。碎片云侵彻能力的影响因素包括碎片云形状、质量分布以及速度等。因此，为了设计更加有效的防护结构，研究弹丸超高速碰撞薄板形成碎片云的质量分布及其随时间变化规律具有重要意义。

对超高速碰撞碎片云进行理论研究非常困难，在二级轻气炮上开展地面超高速碰撞试验是更为有效的研究手段。与试验相比，数值模拟在成本、效率、参数范围以及数据获取等方面存在优势，越来越受到研究者重视，提出了多种工程模型来快速预测碎片云形状、质量分布以及速度分布等特性，郑建东、邸德宁等对此进行了较为系统的综述。Schäfer模型是较为典型的碎片云工程模型，它将碎片云简化为1 个均匀椭球壳、1 个内切于该椭球壳的均匀球壳以及1 个位于碎片云前端的大碎片。黄洁、马兆侠等从碎片云每个碎片的特征量（包括质量、速度和空间角度等）统计规律出发，构建了一个基于概率的碎片云工程模型。这些工程模型的计算效率非常高，但往往过度简化、精度不高。近年来，研究者开始探索神经网络技术在空间碎片防护领域的应用。Ryan 等利用人工神经网络技术预测铝球能否击穿铝板，并与经典弹道极限方程对比，结果表明人工神经网络在训练参数范围内精度较高，主要缺点在于外推能力很差。Hosseini 等采用人工神经网络技术拟合了靶板穿孔直径与弹丸半径、靶板厚度、弹丸质量、碰撞角度、弹丸和靶板材料等因素之间的关系。刘源等基于测量得到的超高速碰撞声发射信号的时域特征、频域特征以及小波能力分数，利用人工神经网络技术自动识别损伤模式（成坑和穿孔等）。

给定一组输入参数，生成一幅灰度图，条件变分自编码器（Conditional Variation Auto Encoder，CVAE）的功能与此类似。本文研究团队前期对采用CVAE 模型预测碎片云形状变化过程进行了初步研究，输入参数为弹丸速度、弹丸半径、靶板厚度和观测时间，输出结果为一个100×100 的矩阵，表征了碎片云的二维质量分布。初步研究结果表明CVAE 模型预测精度远高于传统工程模型，且计算效率远高于数值模拟；但是CVAE 模型也存在一个严重问题，即模型几乎没有外推能力。为改善模型外推能力，本文将像素点的x 和y 坐标也视为输入参数，则预测结果为一个空间点的灰度值（标量），通过采用多层感知机模型（Multi-Layer Perceptron，MLP），根据通用近似定理可以从理论上保证预测精度，从而有可能提高模型的外推能力。此外，对于数值模拟而言，同一组输入参数生成的图像是固定的，导致CVAE 模型中的编码过程并非必要，可以直接对输入参数进行解码，从而得到反卷积模型（De-Convolutional Neural Networks，DCNN）。因此，本文通过系统比较MLP 模型和DCNN 模型，重点考察模型的外推能力。

1 数据与模型

1.1 数据集

本文采用光滑粒子流体动力学（Smoothed Particle Hydrodynamics，SPH）数值模拟结果作为训练集，由PTS 软件批量计算。以弹丸（铝球）超高速正碰撞靶板（铝板）作为算例。坐标原点为弹丸与铝板的初始接触点，以沿着速度方向–4～10 cm、垂直速度方向–7～7 cm 的方形区域（忽略反溅碎片云后部质量较少的区域）作为问题域，将该区域划分为100×100 的网格，统计每个小网格中的总质量m，并以这1×10个数据表征碎片云质量分布。由于每个小网格中的质量相差很大，定义质量对数为（部分小网格中质量为0，则加上一个很小的实数）：

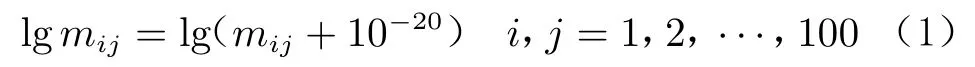
对质量对数进行归一化：

神经网络的输出层采用sigmoid 激活函数，因此模型预测结果是归一化的。参考同样的全局最小和最大网格质量对数，可将模型预测结果还原为真实质量m。

数值模拟中弹丸速度v 的范围为3～8 km/s（间隔1 km/s），弹丸半径r 范围为2～8 mm（间隔1 mm），靶板厚度d 范围为1～4 mm（间隔1 mm），观测时间t 范围为1 ～12 μs（间隔1 μs），共2 016 个数据作为训练集。输入数据同样需要归一化：

需要注意的是：当输入参数在训练集内时，归一化输入参数在0～1 之间；若输入参数大于训练集范围（如测试模型外推能力时），归一化输入参数大于1。

1.2 DCNN 模型

Bhowmik 等采用CVAE 模型对蛋白质折叠进行了模拟，解码器包括1 个全链接层和4 个的反卷积层。本文借鉴该结构设计了如图1所示的反卷积模型。模型采用2 个全链接层升维，通过5 个反卷积层（filters=256，128，64，32，1）加批量归一化层生成最后的质量分布图像。

图1 反卷积模型Fig.1 De-convolutional neural networks architecture

1.3 MLP 模型

第i 行第j 列小网格中的归一化质量对数是归一化弹丸速度、弹丸半径、靶板厚度以及观测时间4 个变量的连续函数：

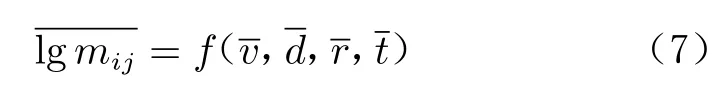
代表像素位置信息的下标i 和j 从离散值（1，2，···，100）扩展至连续值（0～1）：

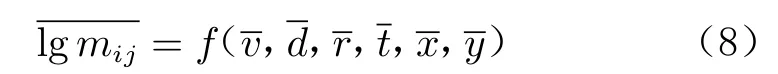
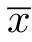
根据通用近似定理，只要神经元数量足够，采用包含一个隐藏层的多层感知机即可以任意精度拟合上述函数。据此设计了如图2所示的多层感知机模型，其中有2 个包含1 000 个神经元的隐藏层。第一层采用ReLU 激活函数，第二层采用sigmoid 激活函数。此外，为了防止过拟合，增加了2 个Dropout层[19]。

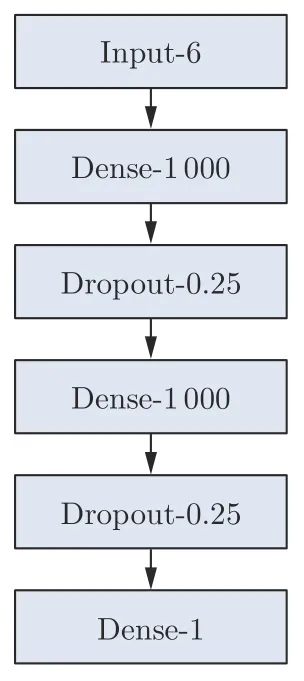
图2 多层感知机模型Fig.2 Multi-layer perceptron architecture

2 模型评估

两种模型实现都采用Keras 函数库，后台使用TensorFlow 深度学习框架执行模型训练。损失函数统一采用均方误差（Mean Square Error，MSE），模型优化使用RMSProp 算法，两种模型的参数数量都在10左右。对于DCNN 模型，在NVIDIA K6000 GPU 卡上训练400 个epochs 大约需要5 h；而对于MLP 模型，训练200 个epochs 大约需要11 h。加载已经训练好的DCNN 模型和MLP 模型后，在i7-6700CPU、内存8G 的台式计算机上生成1 个碎片云图像的平均时间分别为毫秒量级和秒量级。

2.1 模型还原能力

本节考察模型复现训练集中数据的能力。取弹丸速度8 km/s、弹丸半径2 mm、靶板厚度4 mm，此时弹丸半径较小、靶板较厚，弹丸破碎比较严重。图3为此参数条件下的数值模拟和模型预测结果对比。取弹丸速度8 km/s、弹丸半径8 mm、靶板厚度1 mm，此时弹丸较大、靶板较薄，弹丸破碎不严重，形成了一个中心大碎片。图4为在此参数下的数值模拟和模型预测结果对比。

图3 数值模拟与模型预测结果对比（v=8 km/s，d=4 mm，r =2 mm）Fig.3 Comparison of numerical simulations and model predictions（v=8 km/s,d=4 mm,r =2 mm）

图4 数值模拟与模型预测结果对比（v=8 km/s，d=1 mm，r =8 mm）Fig.4 Comparison of numerical simulations and model predictions（v=8 km/s,d=1 mm,r =8 mm）

从图3和4 中可以看出，深度学习模型预测精度远高于传统工程模型。此外，DCNN 模型能够捕捉到碎片云中质量分布的颗粒化性质，而MLP 模型对碎片云中的质量分布进行了均质化处理。

2.2 模型内插能力

考察模型在训练参数范围内的插值能力。取弹丸速度3.5、5.5 和7.5 km/s，靶板厚度1.5 mm，弹丸半径7.5 mm 以及观测时间7.5 μs，共3 个算例，模型预测与数值模拟结果的对比如图5所示。可以看到，插值结果连续且稳定，与数值模拟结果吻合。

图5 模型内插能力（d=1.5 mm，r =7.5 mm，t =7.5 μs）Fig.5 Interpolation capability in the velocity direction（d=1.5 mm,r =7.5 mm,t =7.5 μs）

为了定量描述模型的预测精度，定义每个网格内的相对误差。很多网格内的质量为0，而靶板内部网格质量为常数，可以选为基准。定义每个网格质量相对百分比误差e和总体平均误差分别为：

式中：m为模型预测网格内质量；m为对应网格内真实的物理质量（由数值模拟给出）；m为靶板内部网格真实质量；n 为每幅图片中的网格总数，本文中为10 000。对于上述3 个算例，DCNN 模型的总体平均误差约为1.86%，而MLP 模型的总体平均误差约为0.32%。

2.3 模型外推能力

设计如表1所示的4 组算例，分别测试模型在弹丸速度、弹丸半径、靶板厚度和观测时间4 个变量方向的外推能力。表中加粗数据表示该数据在训练参数范围之外。4 组算例G1、G2、G3 和G4 的数值模拟结果与对应的模型预测结果对比如图6～9 所示。

表1 外推算例参数设计Table 1 Input parameters design for model extrapolation

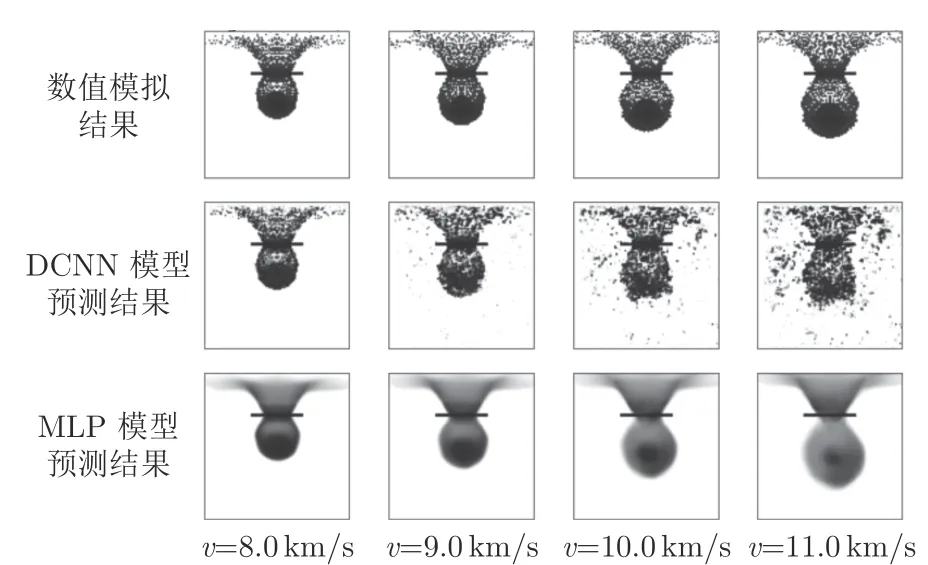
图6 模型在弹丸速度上的外推能力Fig.6 Model extrapolation capability in the velocity direction

从图6和7 可以看到，MLP 模型的外推能力明显优于DCNN 模型。从图7还可以看到，参数r 越大，预测图片上的穿孔直径（图中碎片云与靶板重合区域的横向宽度）也越大，这说明两种模型都学习到了参数r 与靶板穿孔直径之间的关系，但是MLP 模型的外推能力更强。

图7 模型在弹丸半径上的外推能力Fig.7 Model extrapolation capability in the impactor radius direction

从图8可以看到，MLP 模型在d 为6 mm 和8 mm 时预测的靶板不再是标准的长方形，因为预测结果具有一定误差。但从总的趋势来看，参数d 越大，MLP 模型预测的靶板厚度也越大，表明MLP 模型通过学习知道了参数d 与板厚之间的关系，而DCNN 模型没有学习到这一点。

图8 模型在靶板厚度上的外推能力Fig.8 Model extrapolation capability in the target thickness direction

从图9可以看到，DCNN 模型在时间方向上几乎没有外推能力，而MLP 模型能够从1～12 μs 的图像中学习规律，并且以一定精度预测24 μs 时刻的图像。表1中16 个算例的误差分布如图10 所示，可以看到最大平均误差约为4%。

图9 模型在观测时间上的外推能力Fig.9 Model extrapolation capability in the time direction

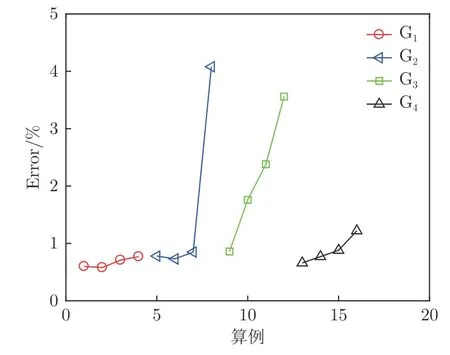
图10 外推算例的误差分布Fig.10 Error distribution for model extrapolation cases

总的来说，多层感知机模型的外推能力明显优于反卷积模型。在图像识别领域，大量研究结果表明，卷积网络结构更倾向于关注图像的纹路等细节特征，而忽略图像的整体形状，这和本文的反卷积模型的表现类似。多层感知机模型的精度有数学定理保证，外推能力也较强。

3 结 论

本文系统比较了反卷积模型和多层感知机模型在预测超高速碰撞碎片云二维质量分布时的优缺点，研究结果表明：

1）在训练参数范围内，反卷积模型和多层感知机两种模型都具有较高精度。

2）反卷积模型能够捕捉到碎片云的颗粒化性质，但是外推能力较差。

3）通过将位置信息加入到标签数据，使得多层感知机模型的精度具有数学理论保证。多层感知机模型对碎片云质量分布进行了局部均匀化处理，外推能力较好。