基于超分辨率重构方法的湍流流场重构

2022-07-14江昊王伯福庄启亮卢志明

实验流体力学 2022年3期

江昊，王伯福,，庄启亮,，卢志明

1.上海大学力学与工程科学学院上海市应用数学和力学研究所，上海 200072

2.上海市力学信息学前沿科学研究基地，上海 200072

0 引言

计算机性能的快速发展和精细化流动测试手段的不断精进，为获取高分辨率流场数据的方法提供了丰富的可能性。在工业上，我们通常希望以较小的计算和实验代价快速获得高分辨率（High Resolution，HR）流场数据。然而，传统的获取高分辨率流场数据方法（加密计算网格、缩短时间步长以及精细化实验测量等）通常都会付出很高的成本。

近年来，研究者开始将超分辨率重构技术应用于获取高精度流场数据。超分辨率重构（Superresolution Reconstruction，SR）方法可以利用低分辨率（Low Resolution，LR）数据重建对应的高分辨率数据。传统的SR 方法主要基于插值算法，例如最近邻插值法（Nearest Neighbour Interpolation）、线性插值法（Linear Interpolation）以及双三次插值法（Bicubic Interpolation，即Bicubic 方法）等。其中，Bicubic 方法重构的数据精度比其他插值方法更高，但是该方法的时间复杂度也是最高的，因此通常被用作超分辨算法的基准线（baseline）。这些插值算法被广泛应用于各个领域，但基于插值算法的超分辨率重构方法的精度依赖于插值点的小范围邻域信息，在较大的下采样比情况下，重构的数据图像往往较为模糊。

同时，机器学习技术也为研究者提供了一种直接从数据驱动角度出发重构高分辨率图像的方法。香港中文大学的Dong 等在2014年首次采用卷积神经网络方法对低分辨率图像进行超分辨率重构，并提出了超分辨率卷积神经网络（Super-Resolution Convolutional Neural Network，SRCNN）。采用SRCNN 方法重构的图像精度和清晰度比传统的插值算法更高，但该方法的网络需要在高分辨率上进行卷积操作，存在训练速度慢的问题。Shi等提出了一种直接对原始低分辨率图像进行网络训练的高效亚像素卷积神经网络（ESPCN）模型，该模型大幅降低了网络训练计算量，提高了重构方法的效率。

近年来，机器学习技术被广泛应用于湍流大数据中。同样地，基于深度学习的超分辨方法也被推广至流场数据重构的应用中。基于深度学习的超分辨率方法的性能依赖于训练数据的完备性。湍流的实验测量和数值模拟获得的数据非常丰富，使得基于深度学习的超分辨率方法成为快速生成高分辨率流场的有效途径。Fukami 等发展了下采样跳跃连接多尺度（Downsampled Skip-Connection Multi-Scale，DSC/MS）混合模型用于二维衰减均匀湍流的单瞬时数据的超分辨率重构，研究了不同下采样方法对DSC/MS 模型的影响，并将DSC/MS 方法推广至时空流场数据的超分辨率重构。Deng等采用两种基于生成对抗网络（Generative Adversarial Network，GAN）的模型—SRGAN 和ESRGAN—对双圆柱绕流的数据进行了超分辨率重构。Bai 等利用字典学习策略对不同状态下的烟雾流动进行了超分辨率重构。Gao 等利用流体力学中的守恒定律和边界条件提出了一种基于物理知识的卷积神经网络，在血管流数据的超分辨率重构和去噪中展现了出色效果。Kim 等采用无监督学习模型和CycleGAN 模型，对湍流场数据进行了超分辨率重构，该模型还可以将大涡模拟数据重构为直接数值模拟精度的高分辨率流场。

本文采用ESPCN 方法和Bicubic 方法对不同下采样比的直接数值模拟所获得的RB 湍流场数据进行超分辨率重构。考虑到实验测量数据中的环境噪声对超分辨率方法存在影响，本文也研究了边界层湍流实验测量数据的超分辨率重构。

1 超分辨率重构方法

1.1 双三次插值方法

在基于插值算法的超分辨率重构方法中，双三次插值方法（Bicubic 方法）是一种高精度的超分辨率重构方法，被广泛应用于图像和数据的处理。

Bicubic 方法是通过在数据中插值来增加或减小局部数据密度，达到改变原始数据精细程度的目的。Bicubic 方法计算了插值点周围16 个数据点（邻域大小为4×4）的加权和，其插值核为：

式中：a 为核函数的参数，在本文中取a=–0.5；d为插值点在i 方向到周围点的距离；x（x）为插值点i 方向的坐标；x（x）为原始流场数据i 方向的坐标；Δx 为原始数据均匀网格的网格大小。

1.2 基于深度学习的超分辨率重构方法

本文采用的基于深度学习的超分辨率重构方法是Shi 等所提出的高效亚像素卷积神经网络（ESPCN）方法。该方法采用三层卷积神经网络重构低分辨率数据，网络架构如图1所示。其中，输入层的低分辨数据是通过Bicubic 方法对原始高分辨率数据（H×W×C；H、W 和C 分别为数据网格高度、数据网格宽度和数据通道数）进行下采样获得，下采样比为r，则下采样后的低分辨率数据的尺寸为（H/r）×（W/r）×C；然后采用卷积神经网络层提取低分辨率数据的特征，相当于通过一组滤波器对图像进行卷积，并将这些特征纳入网络中进行优化；最后采用亚像素卷积层将这些从低分辨率数据中得到的特征上采样重构为高分辨率数据。

图1 ESPCN 模型示意图Fig.1 Sketch of ESPCN

ESPCN 模型训练所采用的损失函数（loss function）为均方误差（Mean Squared Error，MSE）：

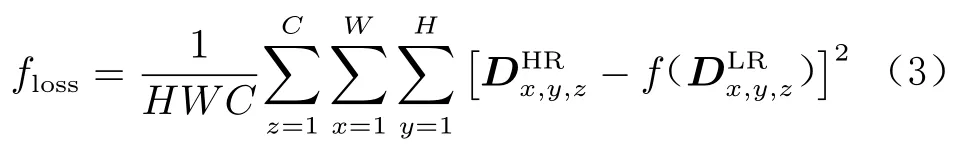
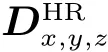
该模型的激活函数为ReLU：并且将70%的数据集用作训练集、30%用作验证集。验证集用于在模型训练时监控当前模型在验证集上的表现能力，为模型超参数的调整提供依据。

2 研究结果

2.1 Rayleigh-Bénard（RB）对流流场重构

首先，研究了直接数值模拟Rayleigh–Bénard（RB）湍流对流数据的超分辨率重构。RB 对流系统的物理模型是一个下底板加热、上底板冷却的对流系统，系统中充满流体介质。由于上下底板温度不同，导致不同高度位置的流体之间存在密度差，系统中的流体在浮力驱动下产生运动。在Oberbeck–Boussinesq（OB）近似下的无量纲控制方程组为：

控制方程分别为连续性方程、含有热浮力项的Navier–Stokes 方程和热输运方程，Ra、Pr 分别为系统瑞利数（Rayleigh number）和普朗特数（Prandtl number）。

通过有限差分法模拟了Pr=0.7、Ra=1×10的RB 对流流场，上下底板温度分别为无量纲温度–0.5 和0.5，计算网格为720×720。分别采用下采样比r为3、10、20 和30 获取低分辨率数据进行模型训练，模型的输入层大小为（720/r）×（720/r）×3，维度3 代表流场数据的3 个通道，分别为温度场、水平速度场u 和垂直速度场v。将70 个瞬时RB 流场数据用于模型训练，30 个瞬时RB 流场数据用于模型验证。图2和3 分别为温度场数据的ESPCN 方法重构结果和Bicubic 方法重构结果（下采样比r分别为3 和30）。

图2 下采样比为3 的RB 系统温度场数据的超分辨率重构结果Fig.2 The super-resolution reconstruction result of the temperature field data of the RB system with rus=3

从图2和3 可以看出，下采样比较小时，ESPCN方法和Bicubic 方法重构的结果都与原始流场数据接近；下采样比较大时，ESPCN 方法和Bicubic 方法在数据过渡比较平滑的中心区域都可以重构出较为精确的流场数据，但在数据梯度较大的边壁区域，ESPCN 方法的重构效果明显优于Bicubic 方法。图4为RB 系统的中心线温度数据剖面（黑色虚线为原始流场结果，红色圆圈为Bicubic 方法结果，蓝色圆圈为ESPCN 方法结果）。

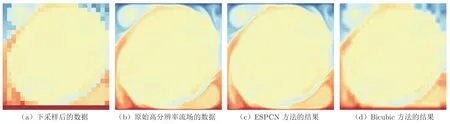
图3 下采样比为30 的RB 系统温度场数据的超分辨率重构结果Fig.3 The super-resolution reconstruction result of the temperature field data of the RB system with rus=30

图4 RB 系统中心线温度数据剖面的超分辨率重构结果Fig.4 Comparison of the results of the temperature profile of the horizontal centerline of the RB system temperature field data

图4描述了RB 系统的水平中心线局部的重构结果对比。下采样比为3 时，ESPCN 方法和Bicubic方法的结果与原始流场数据的水平中心温度剖面基本吻合。下采样比为30 时，在x 坐标靠近0 和1 处，Bicubic 方法重构的温度数据明显偏离了原始数据，ESPCN 方法重构的结果更接近于原始流场数据；在离上下板都较远的bulk 区，可以看出ESPCN 方法重构的温度数据有小范围的偏差。

图5为整个瞬时场的概率密度函数（Probability Density Function，PDF），其中，黑色圆圈为原始流场结果，红色星形为Bicubic 方法结果，蓝色三角形为ESPCN 方法结果。图5描述了整个瞬时场RB 系统温度数据的PDF 分布对比。在两个不同采样比的结果中，ESPCN 方法重构的温度数据分布更接近于原始流场温度数据分布。同样地，下采样比为30时，Bicubic 方法重构的数据在温度靠近–0.5和0.5 附近的分布与原始流场数据分布存在偏差。图4和5 的结果都表明：在数据梯度较大的边壁区域，ESPCN 方法比Bicubic 方法的数据重构更有优势，这与图3的结果也是相吻合的。

图5 RB 系统瞬时温度场数据PDF 分布的超分辨率重构结果Fig.5 Comparison of PDF results of instantaneous temperature field data of the RB system temperature field data

表1给出了不同下采样比的ESPCN 方法和Bicubic 方法重构后的流场数据的MSE。从表中可以看出：下采样比较小时，ESPCN 方法和Bicubic方法重构出的流场误差较小，且两者精度接近；在下采样比较大时，ESPCN 方法的性能优于Bicubic方法。

表1 不同下采样比的MSETable 1 MSE with different down-sampling rus

2.2 湍流边界层流场的重构

上节研究了基于直接数值模拟的RB 系统流场的超分辨率重构。由于存在环境噪声，从实验中获得的流场数据对超分辨率算法具有一定的挑战。本节讨论对湍流边界层（Turbulent Boundary Layer，TBL）实验数据的超分辨率重构结果。

实验测量数据来源于文献[30]，采用粒子图像测速法（Particle Image Velocimetry，PIV）获得。实验装置如图6所示，平板尺寸l×l= 250 cm×80 cm，l和l分别为平板流向和展向长度。平板前缘修型，减小流动分离对下游流场的影响；通过调整平板后缘角度满足零压力梯度条件。自由来流速度u=0.53 m/s。图中绿色区域为实验测量区域，大小为L×L×L63 mm×15 mm×68 mm，L、L和L分别为测量区域的流向、垂向和展向长度。

图6 湍流边界层实验装置图[30]Fig.6 Sketch of turbulent boundary layer experimental device[30]

选取距离平板底部0.41 mm 的二维流场截面（图6中红色线条表示该截面）数据用于训练。被选取的二维截面的网格为64×64，将流向速度u、垂向速度v 和展向速度w 作为ESPCN 的3 个通道的训练数据。同样地，将140 个瞬时TBL 流场数据用于模型训练，60 个瞬时TBL 流场数据用于模型验证。采用ESPCN 和Bicubic 方法对下采样比为2、4、8 的低分辨率流场数据进行重构。图7和8 分别为下采样比为4 和8 的流向速度u 的重构结果对比。

从图7和8 可以看出，对于下采样比为4 和8 的情况，ESPCN 方法仍具有良好的超分辨率重构能力；对于下采样比为8 的情况，以Bicubic 方法重构后的流场数据会丢失掉很多信息，甚至某些尺度较小的速度结构已经无法恢复。

图7 下采样比为4 的TBL 流向速度数据的超分辨率重构结果Fig.7 The super-resolution reconstruction result of the TBL streamwise velocity with the down-sampling rus =4

同样地，图9为下采样比为4 和8 的瞬时TBL流场的流向速度PDF 分布的对比（黑色圆圈为原始流场的结果，红色星形为Bicubic 方法的结果，蓝色三角形为ESPCN 方法的结果）。从图中可以看出，下采样比为4 时，ESPCN 方法和Bicubic 方法重构的流场流向速度分布与原始流场的流向速度分布接近；下采样比为8 时，ESPCN 方法重构的流场流向速度分布比Bicubic 方法重构的流场流向速度分布更可靠。这说明下采样比为8 的TBL 实验流场数据对Bicubic 方法更具有挑战性。