现代试验设计及其在空气动力学中的应用进展

海春龙，何磊，梅立泉，钱炜祺

1.西安交通大学 数学与统计学院，西安 710049

2.中国空气动力研究与发展中心 计算空气动力研究所，绵阳 621000

0 引 言

试验设计是数理统计学的一个分支，是科学试验和统计分析方法相互交叉形成的一门学科。试验设计以揭示设计变量与目标变量之间的关系为导向，选取设计变量空间中具有代表性的向量进行试验并获得结果，通过分析建立具有验证及预测功能的模型。20世纪90年代，NASA 兰利中心将不断发展的试验设计方法理论应用于空气动力学试验，形成了不同于传统单因子试验设计方法（One Fact at A Time，OFAT）的现代试验设计方法（Modern Design Of Experiments，MDOE）并付诸实践。试验设计理论在风洞试验及数值计算中的应用显著提高了试验效率；同时，由于试验和计算的高度复杂性和非线性，使得这一领域的试验设计理论与方法仍然具有极大的发展空间。

试验设计理论与方法众多，各有利弊，彼此又有一定联系。目前与试验设计相关的文献大多结合各领域的背景进行描述，缺乏系统性和通用性。MDOE 方法本身自空气动力学研究中提出，目前快速发展的CFD（Computational Fluid Dynamics）技术、人工智能技术更使试验设计技术成为近年来空气动力学研究的热点之一。本文以空气动力学试验设计问题为背景，介绍不同试验设计方法及其最新进展，演示试验设计方法算例，并对该领域的发展方向进行讨论。

1 MDOE 方法概述

1.1 试验设计问题的基本描述

应用于空气动力学研究的试验设计通常需要考察多个设计变量对目标变量的影响。目标变量往往是性能数据，如气动六分量数据。选取合适的点来反映设计变量对目标变量的影响，从而对尚未试验的点作出良好的估计，是试验设计的首要任务。

1.2 MDOE 方法与OFAT 方法的区别

Giunta 等将经典试验设计限定为全因子设计、中心组合设计、Box-betoken 设计和D 优化方法等，而现代试验设计包括拟蒙特卡罗、正交试验设计、均匀试验设计和拉丁超立方设计等。在空气动力学试验中，两者的区别不仅体现在方法上，更体现在试验思想上：OFAT 是传统试验方法，即固定其他变量进行风洞试验，获取单一变量的数据；MDOE 倾向于统筹全局，从风洞试验中归纳结果、获取知识。MDOE 与OFAT 的主要区别为：

1）试验目的不同。OFAT 方法试图通过覆盖尽可能广的试验参数组合来测试某变量对气动载荷的影响，侧重于直接获取大量风洞试验数据，强调的是通过改进风洞模拟的真实性和测试手段来提高试验数据的精准度；MDOE 方法则是以精心设计试验为基础，通过开展少量风洞试验来建立模型，进而获取科学结论。

2）试验过程组织策略不同。OFAT 方法以获取大量丰富的数据为目的，对试验对象气动特性的先验信息依赖小，试验方案规模较大，资源消耗大；MDOE 方法以揭示变量间的关系为目的，对试验对象气动特性的先验信息依赖相对较大，试验方案需要精心设计，且可能出现分阶段增加试验样本点的情况，但资源消耗相对较小。

3）试验结果及其使用方式不同。OFAT 方法产生的是结构化的气动数据，主要用于构建试验对象的基准气动数据集，通过插值获取输入状态下的气动数据；MDOE 方法生成的数据通常是非结构化的，需要先对数据建模，然后通过模型来开展后续应用。

2 MDOE 方法研究进展

MDOE 方法主要包括试验设计、试验实施、试验分析3 个环节，流程如图1所示。不同的设计问题可能会有不同的结束条件，比如建模次数或邻近两次建模函数结果作差等。

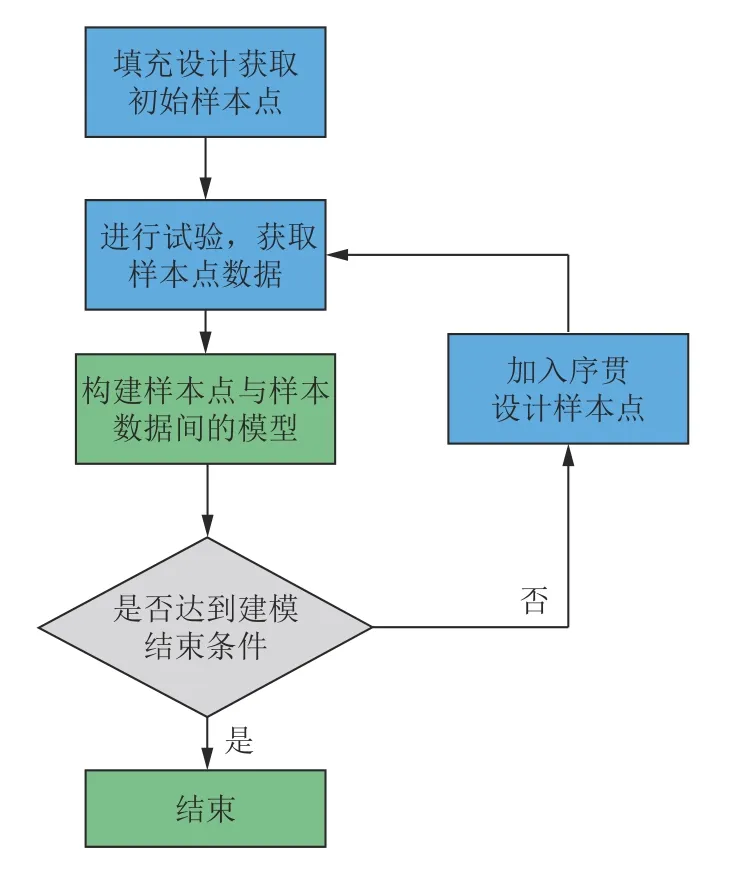
图1 MDOE 方法流程图Fig.1 MDOE method flow chart

整个流程可以概括为以下3 个步骤：1）进行全空间填充试验设计，确定初始选点方案；2）进行风洞试验；3）基于风洞试验结果进行分析，一般包括构建模型（或确定模型参数）以及误差和不确定性分析，根据分析结果进行序贯设计。相关理论方法主要涉及第1 步和第3 步，包括4 个方面：填充设计、序贯设计、模型构建和结果分析。

2.1 填充设计

20世纪50年代，Fisher 创立正交试验设计方法，系统给出了实现方法及其方差分析模型。国内学者简化了正交试验设计的应用方法，编写了系统的正交试验表。正交试验设计方法有如下要求：

1）任一设计变量的诸水平做相同数目的试验；

2）任两个设计变量的水平组合做相同数目的试验。

对于固定设计变量个数和水平组合数的问题，可以给出正交设计表。正交设计表有如下要求：

1）任一列的诸水平的重复数相同；

2）任两列所有可能的水平组合有相同重复数。

正交试验设计要求一种数学上的紧凑性，有利于后续的数据分析，更容易得出可靠的结论。

王元教授和方开泰教授创立了均匀性评价准则和均匀设计方法。在能够确定模型形式的情况下，正交试验设计往往事半功倍；但若模型未知，正交试验设计的试验摸索往往耗时费力。方开泰提出的均匀设计对真实模型的逼近能力更为稳定，其理论对均匀性的定义以中心化L偏差表示。而对均匀性理解的不同，或者评价标准的不同，会产生不同的均匀设计方法。因此，关键在于对均匀性的定义，设计良好的均匀性标准，然后给出满足此均匀性的试验设计方法。

从均匀设计的理念出发，需要考虑的是在给出要求的试验点个数的同时如何兼顾均匀性。均匀设计的求解是一个优化问题，而求解是在离散空间中进行的，缺乏有效的优化手段。针对此问题，发展了多种方法直接构造或者近似求解均匀设计，其中最为常见的是拉丁超立方设计（Latin Hypercube Design，LHD）。LHD 是一种行之有效、应用广泛的试验设计方法，取样均匀，适用于影响因素较多的情况，可显著降低试验规模。LHD 的选点方式确保了在每个维度上选点均匀，但这种均匀性并非全局均匀性的等价条件，有时会出现质量不高的选点设计。因此基于拉丁超立方设计发展了多种改进策略，例如最大最小距离准则、减少相关性准则、最小综合均方误差准则和极大熵准则等。

香农最早提出用“熵”的概念描述信息量，在试验设计中，同样可以用“熵”的概念衡量试验设计获取的信息。采用极大熵准则，使得一次试验设计获取的信息量最大，即相当于一次试验设计样本点集P的先验协方差矩阵行列式最大：

式中，为样本点的先验方差，为样本点的相关系数矩阵，为可以选择的先验协方差函数。假设样本点间的先验协方差函数为高斯函数，则：

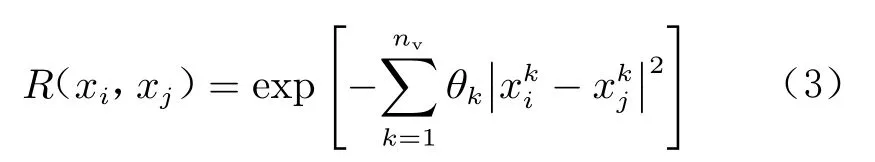
式中，n为样本点向量的维数，为未知相关参数。可由最大似然估计法计算得到，通过优化下式可以得出的值：

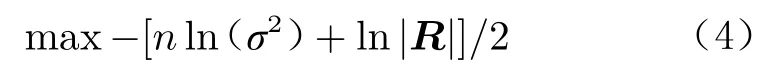
而对于已有样本点集P={x，x，…，x}，选择增加一个样本点x使其获得的信息极大，即熵极大，可通过优化下式得到x的选点位置：

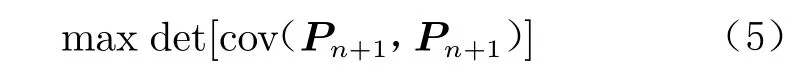
式中，

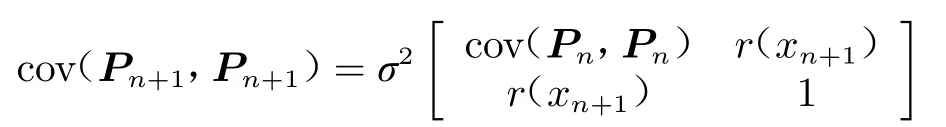
其中，

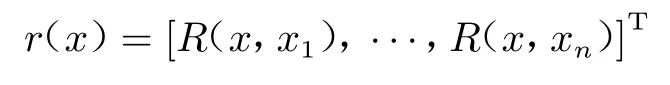
作为一种极为常用的试验设计方法，拉丁超立方设计是均匀设计的一种近似求解方法，极大熵准则的应用则是对拉丁超立方设计的改进。以先验矩阵行列式的值最大来定义点之间的混乱程度最高；行列式的值高，代表矩阵行向量之间的无关性达到最大，倾向于获取全空间信息的初始样本点集。因此，在对问题特异性尚不清楚的最初阶段，利用极大熵准则获取首次试验点，能够在全空间获取全面信息，提高近似模型的精度。

2.2 序贯设计

在MDOE 方法的应用过程中，发现组织一次试验往往并不能达到最终需要的效果。为了避免各种资源的浪费，在试验开始阶段往往倾向于选取较少的试验点，然后进行序贯加点。序贯加点的准则有两种，其一是以模型误差为依据，增加预估误差较大的试验点，从而减小模型误差，包括交叉验证准则、累积误差准则等；其二是以模型优化为依据，主要包括最小化代理模型预测误差准则、期望提高准则和均方差准则等。

实际上，序贯设计是试验设计内涵与所用建模过程数学内涵的紧密结合。以机器学习建模过程为例，机器学习的目的在于建立具有良好泛化能力的模型；试验设计则是通过设计试验点的选取，达到用更少的点获取更多空间信息及问题信息的目的。带有不确定性评估的机器学习模型可以给出用以改善不确定性的点，从而产生一种序贯加点准则。序贯加点设计可以明显降低选点数量。常用到的序贯加点准则如下：

最小化代理模型预测误差准则是操作最为简单、最为直接的加点准则，通过直接求解代理模型的最小值点，作为增加的样本点进行序贯设计。其求解问题主要为：

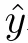
期望提高（Expect Improvement，EI）准则也称为高效全局优化（Efficient Global Optimization，EGO）准则。其求解问题主要为：

基本思想是通过计算目标函数提高的期望，把期望最大值点作为新样本点。程诗信将这一思想推广到处理多目标函数的情况，提出了一种超体积算子与EI 函数相结合的加点准则，该准则适用于多目标设计变量的问题。王彦将目标函数提高的期望分解为两部分，一部分描述局部搜索能力，一部分描述全局搜索能力，通过对这两部分赋予不同的权值构建了不同的算法。

均方差（Mean Square Error， MSE） 准则是Kriging 代理模型中的一种加点准则，直接运用Kriging 代理模型提供的均方差估计最大处作为新样本点的位置。均方差估计如下：

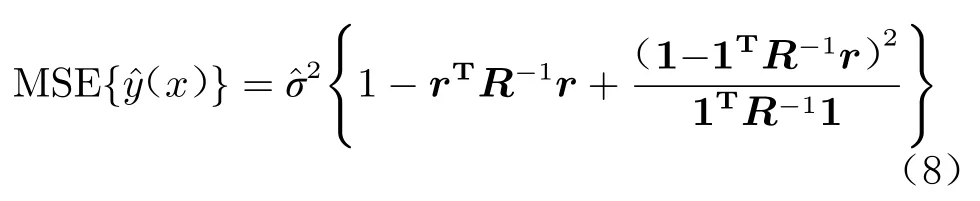
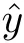
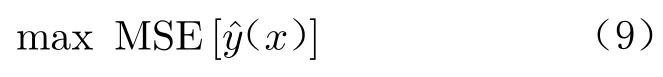
上述3 种准则的序贯设计方法有一个共同点，即运用加点准则获得相应的优化问题，通过求解优化问题确定新的样本点。

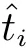
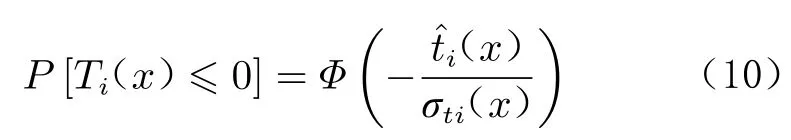
加上约束条件，优化问题变为：

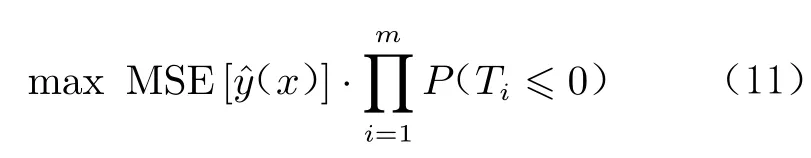
对于最小化代理模型预测误差准则，利用遗传算法进行序贯设计时，也有类似的对约束的处理方法。对于期望提高准则，文献发展了类似于上述约束的改进EGO 算法。

交叉验证准则是考虑误差大小的一种加点准则。对于由n 个样本点构成的样本点集P={x，x，…，x}，去掉其中一个样本点x（1≤i≤n），用剩余样本点构成的集合建立近似模型，以此模型估计样本点x的值，并计算该点的交叉验证误差e：

交叉验证误差能够在一定程度上体现近似模型在各个样本点附近的可信度和规则程度，交叉验证误差越大，可信度越低，不规则的概率越大。因此，交叉验证准则就是以所有样本点的交叉验证误差为基础，对全局空间设计点的误差进行估计，将最大的误差估计点作为新点加入样本点，以此增加对不可信区域或不规则区域的抽样数量，提高在该区域的近似精度。全空间误差估计近似模型表示如下：

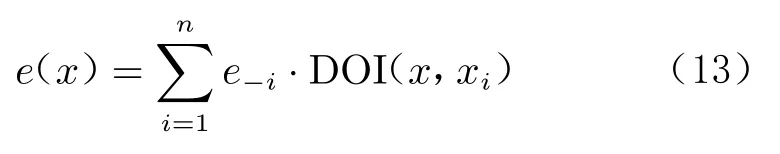
式中，DOI（x，x）表示样本点x对点x 的影响度，亦即两点间的相关性。目前有很多相关函数可用于描述设计空间两点间的相关性。例如高斯函数：

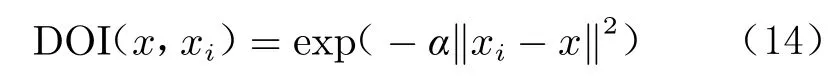
式中，为自定义系数。当样本点增加时，若对每一个点都进行交叉验证，就会耗费大量计算时间，大大降低效率。从式（12）可以看出，交叉验证误差越大的点对全空间误差估计的贡献越大。因此，从提高交叉验证效率的角度出发，发展出了部分交叉验证思想，即通过对部分关键点的交叉验证估计全局近似误差。

序贯建模累积变化准则用于记录序贯建模过程中全空间各点误差随模型的不断改变而累积的变化。设定累计变化如下：

式中，为权重系数。模型在序贯累积误差大的点具有较低的可信度，可以此为准则获取极大序贯建模累积变化点对样本点集进行扩充，提高该区域的近似精度。通过式（15）优化，可获取极大序贯建模修正累积变化点，将其加入样本点集更新模型，即可有针对性地提高模型在不规则区域或低可信度区域的近似精度。

在实际应用中，可以采取多准则结合的方式提高效率和效果。姚雯、Giunta和Swiler等提出了综合应用极大熵准则和拉丁超立方设计进行全空间填充设计的方法，以该方法构造初始样本点集，然后运用部分交叉验证和累积误差准则进行序贯设计，并给出了完整的试验设计流程。杜丽等提出了一种适用于约束空间的多准则加点方法。张泽斌等结合“MSE 和EI”的并行加点准则进行了试验设计。

对于多项式模型，有一类基于模型信息矩阵的加点方法。多项式模型可表示为：

式中：

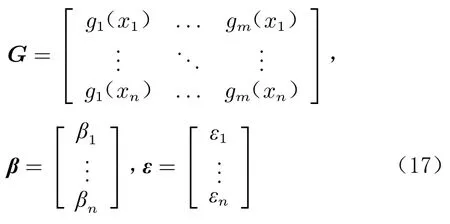
矩阵G 为结构矩阵，它既包含了试验设计的信息，又包含了拟合模型的信息；参数为模型系数；为随机误差，误差的期望为0，先验方差为。

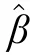
式中：取决于方法外的其他因素；信息矩阵M=GG，式中要求M 是非退化的。通常希望通过试验最准确地建立模型，即对参数作最准确的估计，根据这一要求来设计因素x 的取值。基于这一思想，产生了“最优设计”的概念（这种“最优”是指统计范式下的最优）。通过选择试验点，使得信息矩阵包含更多信息，对矩阵大小比较的定义不同，就产生了不同的最优设计方法：

D–最优设计：取试验点使M 行列式值达到极大；

A–最优设计：取试验点使tr（M）达到极大；

E–最优设计：取试验点使M的最大特征根达到极小；

G–最优设计：取试验点使响应预报值的最大方差达到极小。

以上最优设计方法都是通过增加序列、减少样本点来实现，因此可视为序贯设计策略。

2.3 模型构建

试验样本为建立模型提供数据，新样本点的加入能提升模型的精度和泛化能力，而模型本身的预测和泛化能力又会对样本点的选取产生影响。因此，无论是依据试验结果构建模型还是确定模型参数，试验设计与模型选取都是息息相关的。目前工程上常用的方法主要分为两类，一类是基于机理建模的方法，如多项式模型、径向基函数、混沌多项式模型和基于对称性的三角多项式模型等，其核心思想是运用某一个完备的函数空间，通过确定合适的线性组合系数，使模型更准确地拟合现有数据；另一类方法是包括机器学习在内的多种黑箱模型，比如Kriging 模型、高斯过程、支撑向量机、BP 神经网络模型决策树方法、模糊逻辑建模方法、RBF 神经网络建模方法等，而神经网络模型又有浅层网络和深层网络之分。这些方法的基本思想是通过训练样本数据的学习，对模型的结构、权值参数进行调整，建立随机过程、神经网络等输入–输出之间的映射模型，使其对数据具有最佳的拟合及预测效果。两类方法各有优势与弱点：运用机理建模方法构建的模型，往往能对其组合项进行物理含义解释，因此模型更具有普适性和较强的泛化能力，但拟合能力较差；包括机器学习在内的“黑箱”建模方法对非线性数据的拟合能力通常优于机理建模方法，但泛化能力较弱，可解释性差，增加网络层数可以改善泛化能力，但需要增加样本量。

在近年的相关研究中出现了一些改进模型，例如，Li和Khang等采用试验设计方法研究翼型性能对翼型几何形状的总体响应，构建了多项式模型，提出了一种筛选多项式项的方法；Thurman 等在水动力试验中提出了统计预测元模型，Thiele和Golovnya等提出了交互图模型，Wang和Meng等在这方面也做了大量工作，提出了多种组合网络模型。

2.4 结果分析

MDOE 方法往往以获取知识为目的，这些知识一方面包括代理模型本身，另一方面也包括模型中各变量的影响规律。通过影响分析，可以更好地指导序贯样本选取，获得更为准确的代理模型。目前比较通用的影响分析方法包括总响应面分析、导函数分析、干扰分析、图标分析、识别基础模型、多目标优化等，此外还有对灵敏度、不确定性和数据关联性等目标的分析方法。近年来，设计变量影响分析的研究大都从上述几个方面开展工作，有学者在吸进式高超声速飞行器中实现了参数化建模、正交试验设计、CFD 气动性能计算和方差分析相结合的灵敏度分析方法；也有学者用自组织映射等方法分析了飞行器设计参数与气动结果之间的数据相关性。在多数情况下，协同使用多种数据处理手段对结果进行分析，以达到综合验证和对比的目的。

3 试验设计方法算例

针对两个典型算例，同时采用均匀设计和序贯设计方法，建立BP 神经网络模型和Kriging 模型，基于建模误差对两种试验设计方法进行验证和对比分析。

3.1 一维标准函数算例

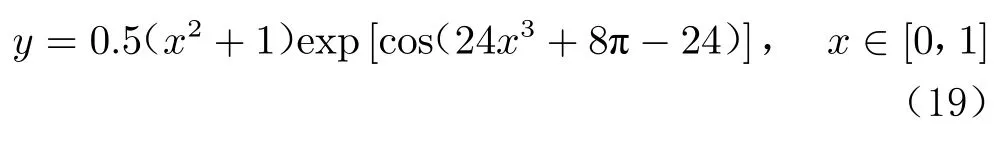
考虑一维函数式：该函数在前一小段较为平滑，而后段频率较高，以此来验证均匀设计和序贯设计的不同效果。

以BP 神经网络模型进行拟合，序贯设计采用交叉验证准则。图2为序贯设计结果，靠近底部的虚线高度代表全空间误差大小，每次选取全空间误差最大处作为下一步加点。可以看出，序贯设计曲线与真实曲线吻合得很好。

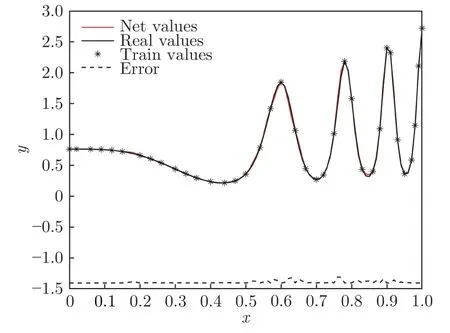
图2 BP 神经网络序贯设计误差图Fig.2 BP neural network sential design error plot

表1给出了模型的最大误差和均方差，可以看出：随着样本点增加，模型的结果越来越准确；在每一组相同的样本点中，序贯设计都比均匀设计更为准确。

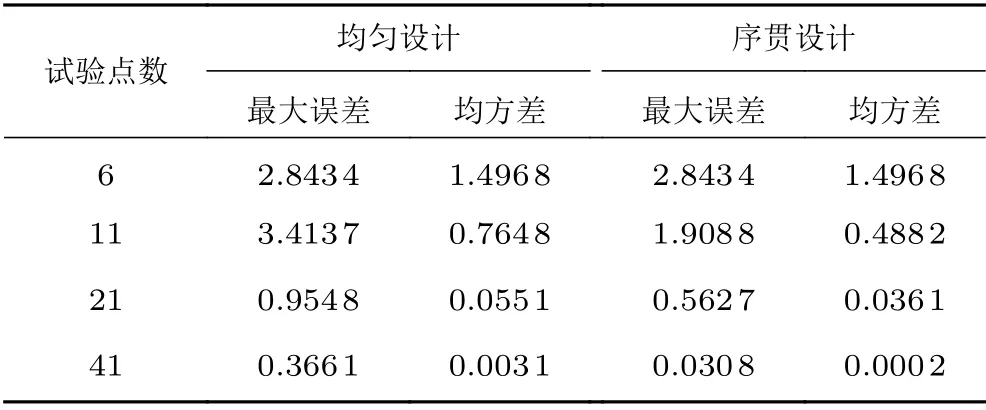
表1 BP 神经网络模型误差表Table 1 BP neural network model error table

使用Kriging 模型进行拟合，序贯设计采用最大均方差准则。图3给出了Kriging 模型的序贯设计结果。图中蓝点标注了均方差最大的位置，即下一步需要添加的点，可以看出序贯设计结果与真实函数曲线吻合较好。

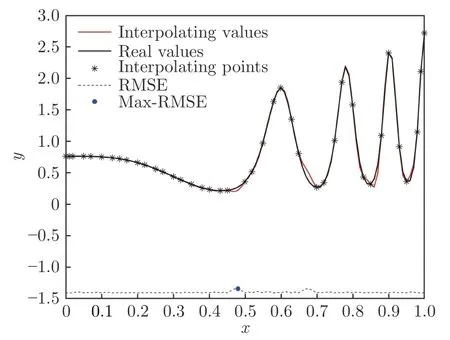
图3 Kriging 序贯设计结果Fig.3 Kriging sential design result plot

表2给出了模型的最大误差和均方差。可以看出：随着样本点增加，模型的结果越来越准确；序贯设计的最大误差结果更好，均方差有更快的下降梯度。

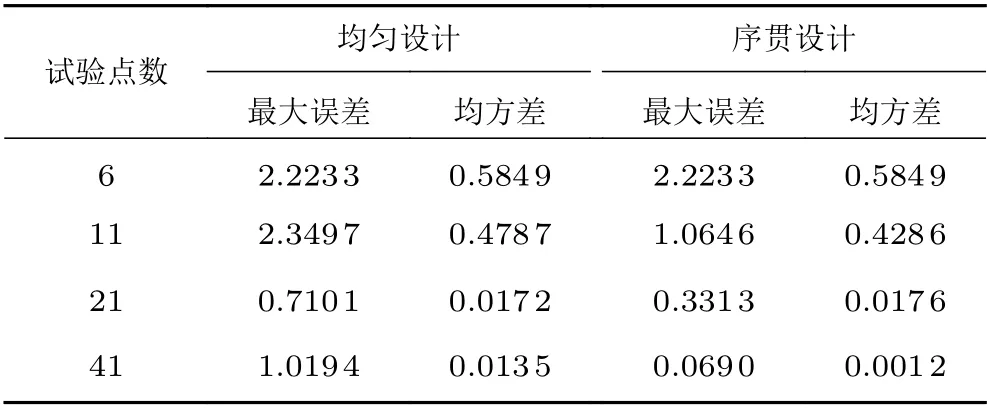
表2 Kriging 模型误差表Table 2 Kriging model error table

3.2 空气动力学算例

以钝锥标模计算得到的阻力系数为研究对象，以马赫数Ma 和迎角为设计变量（马赫数变化范围0.4～7.0，间隔取0.1；迎角变化范围0°～25°，间隔取0.5°），进行数值计算，获得气动阻力系数C，结果如图4所示，可以看到跨声速段的气动特性变化较为剧烈。

图4 气动数据图Fig.4 Pneumatic data plot

以BP 神经网络模型对气动数据进行拟合，序贯设计采用交叉验证准则。图5为序贯设计结果。表3给出了不同设计方法的最大误差和均方差。可以看出，无论是最大误差还是均方差，神经网络模型的序贯设计结果都明显优于均匀设计。

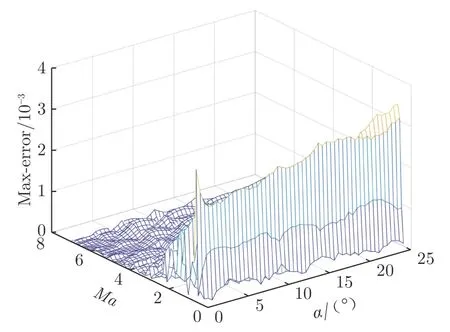
图5 BP 神经网络序贯设计误差图Fig.5 BP neural network sential design error plot

表3 气动数据BP 神经网络模型误差表Table 3 Pneumatic data BP neural network model error table

使用Kriging 模型对气动数据进行拟合，序贯设计中使用最大均方差准则。图6为Kriging 模型的序贯设计结果。表4给出了不同设计方法的最大误差和均方差。从表中可以看出：随着样本点增加，模型结果越来越准确；在相同样本点数下，序贯设计比均匀设计具有更高的精度。

表4 气动数据Kriging 模型误差表Table 4 Pneumatic data Kriging model error table

图6 Kriging 模型序贯设计误差图Fig.6 Kriging sential design error plot

以上4 组算例都显示了序贯建模的优势；另外，从一维函数和气动数据两个问题均可以看出，在相同取点规模下，BP 神经网络模型结合交叉验证的建模精度略优于kriging 模型结合最大均方差准则的建模精度，这说明样本与模型之间具有关联，需要根据研究对象选取样本和模型。

4 试验设计后续重点发展方向

近年来，随着信息化技术和智能技术在风洞试验中的应用，风洞试验呈现出日益精细化的趋势，科学、高效、智能是试验设计技术的主要发展方向。

1）序贯试验设计与模型的紧密耦合。与其他试验设计相比，序贯试验设计更高效、资源消耗更少，模型选取和样本点选取有很强关联。例如，在神经网络模型中，模型构建与选点位置相互影响，因此以模型优化为目标的序贯试验设计方法的创新与应用是主流方向，在实践中需要根据不同的模型采用不同的加点策略。例如，目前广泛采用的深度神经网络模型对样本需求量较大，可以通过生成对抗网络（Generative Adversarial Network，GAN）方法产生满足试验设计需求的样本。

2）融入物理知识的试验设计。现有试验设计方法大多依据数学理论描述的评价进行选点，而空气动力学所研究的问题都具有较强的物理背景，在激波、分离点等流动特性变化比较剧烈的位置，需要适当增加样本点。例如，文献在气动优化试验点选取中加入了对流动状态的考量。在现有试验设计方法中，如何对知识进行有效描述以及如何将知识融入试验设计过程都需要开展深入研究。

3）试验设计统计学理论的深入研究。试验设计本身来源于统计学理论，因而对试验设计方法的基础理论研究也是一个研究重点，例如对不同试验方法所能实现的精度的统计学分析描述、对所用数据建模的可解释性等。文献对机器学习可解释性在数据建模领域的应用进行了有益的探索。

4）样本空间搜索策略的改进完善。理想的样本空间搜索策略是：不遍历样本空间即可快速找到目标函数全局最优点。这一方面需要搜索算法具有较强的全局搜索能力，另一方面也需要对目标函数特性有较为准确的描述。可以考虑的方法包括采用多条并行马尔科夫链进行空间探索，例如文献中的多链算法；或是采用序贯加点准则和随机搜索策略相结合的试验设计方法，例如文献中的激励探索策略。在结合得当的情况下，这些方法有望增强加点方式的自适应能力，从而进一步增强试验设计的实用性。

5）多源数据融合分析时的试验设计理论与方法研究。目前的试验设计研究主要针对的是单一手段的试验过程，而空气动力学研究常常要面对三大试验手段（风洞试验、数值计算和飞行试验）提供多源数据条件下的试验设计问题。在此情况下，应进一步考虑多源数据之间的冗余性、衔接性、关联性以及精度匹配等。将试验设计的理念有效推广至多源数据、多准则、多模型的试验设计，在空气动力学研究中将具有更强的理论与实用价值。