基于多源数据融合的翼型表面压强精细化重构方法
2022-07-14赵旋彭绪浩邓子辰张伟伟
赵旋,彭绪浩,邓子辰,张伟伟
西北工业大学 航空学院,西安 710072
0 引 言
现有风洞试验中的载荷测量主要包括直接力测量和表面压力测量,飞行器风洞缩比模型也因此分为测力模型和测压模型。总体而言,风洞试验的可信度较高,获取的气动力/载荷结果往往作为考核数值仿真方法精度的标模。然而,由于风洞试验的周期较长,对试验人员的经验性依赖较高,试验方案的合理性直接影响气动载荷的获取效率和效果。现有的工程实践普遍认为翼型表面至少需要布置50~100 个测压孔,经过压力分布积分得到的升力和俯仰力矩系数精度才较为可信。为获得翼型表面完整的流场信息,传统方法通常在翼型表面布置足够多的测压孔进行风洞试验,通过简单的插值重构获得翼型全表面的压力分布,这往往需要较多的测压孔。对于复杂飞行器,受限于空间位置和试验成本,测压数据获得不充分,使得这种传统的方法精度不够;且复杂飞行器跨声速风洞试验的气动载荷受参数影响敏感,精细化的气动力/载荷的测量难度更大、周期更长,因此亟需发展一种利用有限测量点流场数据重构复杂飞行器表面流场信息的方法。
数据融合技术针对多种来源信息(同质或异质),根据某种标准在空间或时间上进行组合,获得被测对象的一致性描述,并使得该融合系统具有更好的性能。目前,在空气动力学领域中,已经开展了多种多源信息融合方面的研究。Belyaev 等利用CFD 计算数据与风洞试验数据融合构建了非均匀、非完整试验状态空间中的代理模型,并利用风洞试验数据验证了模型的精度。Ghoreyshi 等利用试验数据与 CFD 计算结果构建了飞行器的高维变精度气动力模型。王文正等提出了基于数学模型的气动力数据融合准则和方法,以气动力数据满足的准则为依据,将不同类型的数据进行融合。Wang 等利用本征正交分解(POD)技术分别得到低、高精度流场数据的低维表示,通过 Kriging 模型建立两者的映射关系,实现了不同状态的定常流场融合预测。Kou 等采用多核神经网络模型将变精度模型推广到非定常气动力模型中,实现了利用低精度欧拉结果对 N–S 数值结果的逼近。He 等采用Kriging 模型构建气动热流分布数据融合模型,获得了较好的效果。Misfud 等采用Gappy POD 结合风洞试验数据和CFD 计算数据构建了针对二维翼型和三维翼身组合体的数据融合模型,利用正则化方法提升了模型的预测精度。Perron针对不同构型表面压力分布场,采用POD 和流形对齐构建了高维数据融合模型,但是建模效果有待提高。Renganathan等发展了基于贝叶斯理论框架和带约束的本征正交分解技术,用于解决带噪声的不完整风洞测量场与确定但有偏的数值模拟场的融合问题。Sun 等开发了一种快速风场重建方法,提出一种传感器布局优化求解过程,基于传感器获得的有限测量数据,通过POD 技术对风场进行逆过程快速重构。Zhao 等提出了基于压缩感知算法的针对翼型表面进行压力分布重构的方法。Li 等基于深度神经网络,融合风洞试验数据和CFD 计算数据,预测了机翼不同状态、不同截面的压力系数。
现代数值模拟规模和分辨率的提高,提供了大量仿真数据,因此本文提出了一种融合有限的风洞试验数据和数值计算(CFD)数据的新方法,通过本征正交分解技术对仿真得到的压力分布数据进行特征提取,然后融合稀疏的风洞试验测压数据,基于压缩感知(Compressed Sensing,CS)算法进行分布载荷精细化重构研究。与Misfud、Renganathan等工作的不同之处在于:本文采用稀疏的试验测压数据进行压力分布重构,通过压缩感知算法求解基函数对应的坐标,提高了方法的鲁棒性,对于变几何变来流状态算例仍具有较好的适应性,对不同翼型具有较好的泛化性,且积分获得的升力系数和俯仰力矩系数精度较高。
1 研究模型及方法
1.1 研究模型
算法框架如图1所示,主要包括以下4 个方面:
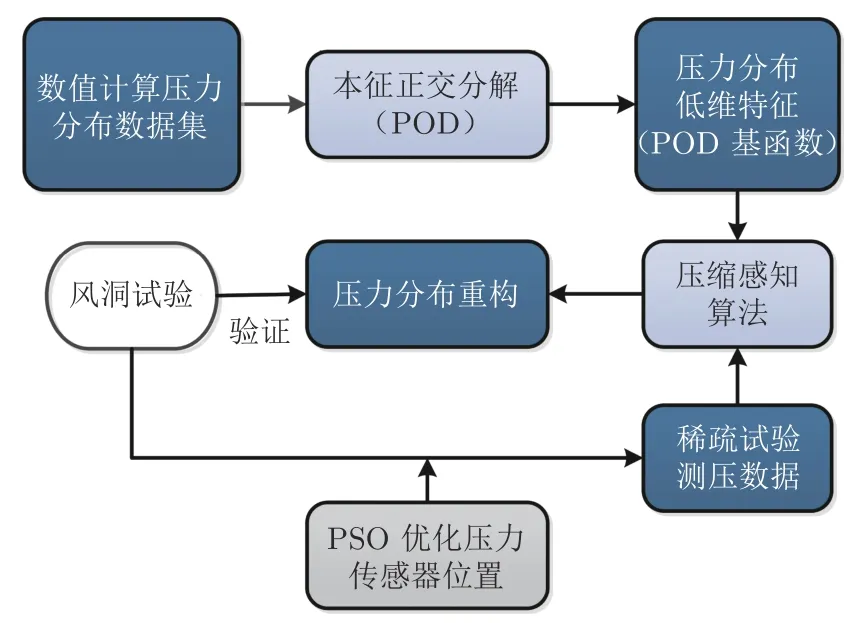
图1 算法框架流程Fig.1 Algorithm framework process
1)使用CFD 方法计算不同工况下(几何改变、状态改变)的压力分布数据。
2)采用本征正交分解技术提取CFD 计算的压力分布数据的低维特征,即POD 基函数。
3)优化翼型表面压力传感器位置:采用粒子群优化算法(PSO)获得最佳测量点位置。
4)利用有限试验测压数据,基于压缩感知算法进行压力分布重构,对压力分布进行积分获得升力系数和俯仰力矩系数,并通过试验数据进行验证。
1.2 研究方法
本文中算例均为定常流动,CFD 求解器基于定常雷诺平均Navier-Stokes(N-S)方程,求解方法采用二阶有限体积法,空间离散格式采用Roe 格式,采用伪时间推进法,通过隐式Gauss-Seidel 迭代求解。
本征正交分解技术是一种常用的降维手段,能够将复杂动力学从高维离散化系统投影到低维系统。该技术的本质是通过对流场样本进行矩阵变换及正交分解,得到使样本残差最小的若干正交基函数,用于描述流场的主要规律。基于POD 技术,根据特征值的大小对模态按照能量进行排序,可以提取出主要的流动模态。通常采取降维方式简化模型:按能量截取一个维数为M(M<<N)的低维空间(式(1))使()≥;一般取99%(略小于1),以捕获绝大部分能量。
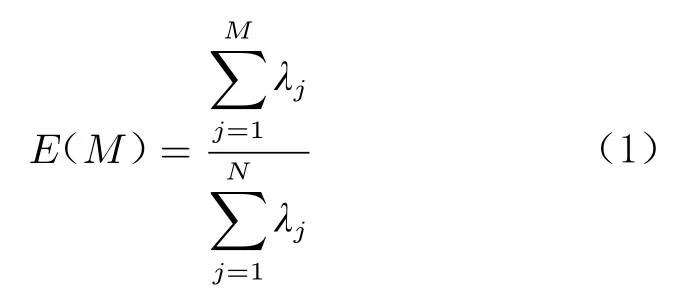
其中,N 为样本空间维度,为特征值大小,为能量大小。
粒子群优化算法是一种进化计算技术,其基本思想是通过群体中个体之间的协作和信息共享来寻找最优解。本文使用粒子群优化算法获得测压点位置,基本步骤如下:
1)将CFD 所计算的压力分布数据分为两部分,一部分为训练集,另一部分为测试集,基函数在训练集中通过POD 获取。
2)在测试集中选取一部分压力分布数据,通过粒子群优化算法,测量点遍历翼型上所有点,通过压缩感知算法重构流场,以重构误差作为判断标准。
3)输出一组使重构误差较小的测量点位置,将输出的测量点位置用于压力分布重构。
压缩感知技术突破了香农采样定理的局限,可用较少的数据实现高精度的完整信号重构。压缩感知技术一经提出即引起广大研究者的兴趣,被广泛应用于地理、航天、通信等各个领域。压缩感知基本框架如图2所示。假定观测值y ∈R是通过测量矩阵φ ∈R建立在原信号x ∈R上得到的,即=,压缩感知的目的是通过稀疏的观测值恢复原信号(欠定条件下,M<<N)。

图2 压缩感知框架Fig.2 Compressed sensing framework
信号通过稀疏矩阵可以进行稀疏表示,即:

因此,方程转化为:
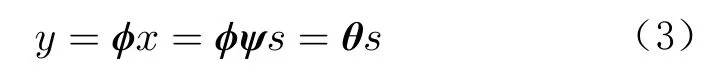
可通过下面的优化问题近乎完美地从y 中恢复出稀疏信号s,进而恢复x:

上式即L0 范数最小化问题。若直接求解式(4),则是一个N-P hard 问题。在一定条件下,L1 范数最小化与L0 范数最小化共解,于是式(4)转化为:

本文将POD 和CS 技术相结合,原信号x 为翼型表面完整压力分布,观测值y 为稀疏的压力试验数据,算法如下:
1)通过POD 提取CFD 计算得到的压力场数据,得到POD 基函数,即提取计算数据的低维特征。
2)对翼型表面进行压力点采样,即=,为测量矩阵,y 为采样点压力值。
3)基于压缩感知技术进行流场重构(L1 范数最小化)。
2 算例验证
2.1 亚声速流动
采用CFD 计算了132 组NACA0012 翼型亚声速状态的压力分布数据(马赫数Ma=0.1~0.6,迎角=0°~11°),采用本征正交分解技术提取了8 组CFD 计算数据的POD 基函数,采用粒子群优化算法得到4 个测压点位置,并基于4 个测压点处的数据进行重构。CFD 计算NACA0012 翼型采用的结构化C 型网格如图3所示:
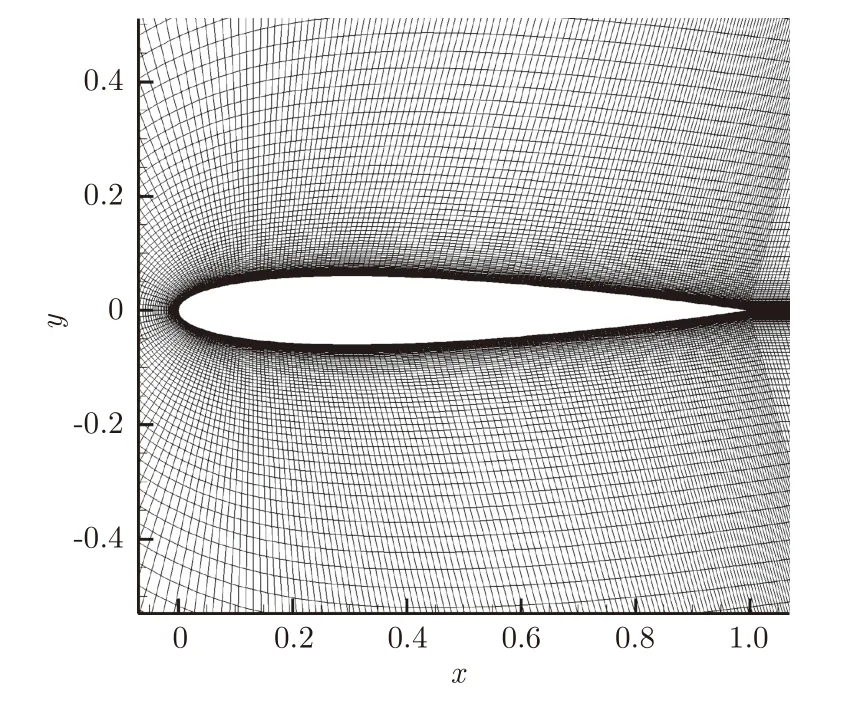
图3 NACA0012 翼型网格Fig.3 NACA0012 airfoil grid
为了量化说明重构流场与实际流场的偏差程度,定义误差如下:
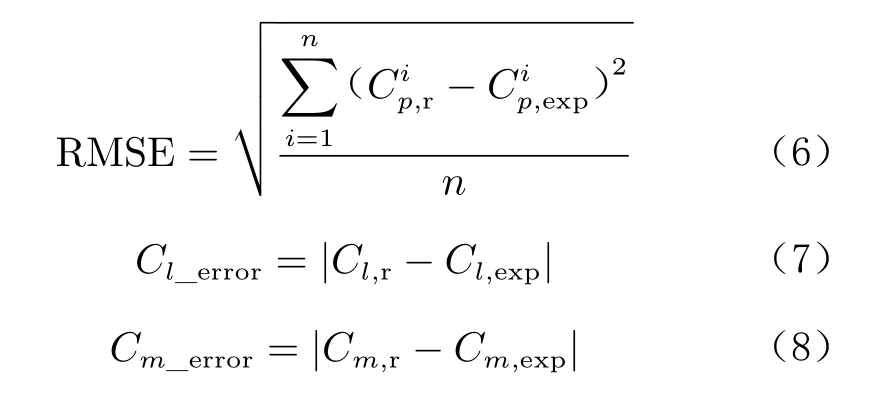
其中:RMSE 为均方根误差;C为重构得到的压力系数,C为试验测得的压力系数;n 为翼型表面试验压力点的个数;C为通过重构的压力分布积分得到的升力系数,C为试验数据对应的升力系数;C表示通过重构的压力分布积分得到的俯仰力矩系数,C表示试验数据对应的俯仰力矩系数;C和C分别表示升力系数和俯仰力矩系数重构值与试验值之间的误差,俯仰力矩系数是对翼型1/4 弦线处进行积分的。
图4为NACA0012 翼型在Ma=0.3、=0.106 9°、Re=6.0×10工况与Ma=0.3、10°、Re=6.0×10工况的重构结果及其与试验、CFD 数据的对比,两组工况的试验数据与重构数据之间的RMSE 分别为 0.042 1、 0.074 5。 图5为 NACA0012 翼型在Ma=0.504、=4.06°、Re=3.8×10工况下的重构结果与试验、CFD 数据的对比,试验数据和重构数据之间的RMSE 为0.064 1。图中蓝色虚线为CFD数据,黑色实线为重构曲线,红色空心三角形为试验数据,绿色实心倒三角形为所采用的测压点数据。表1给出了图5对应试验状态的升力系数和俯仰力矩系数以及对应误差,表2给出了较多试验工况下重构的升力系数和俯仰力矩系数误差上下限统计结果。通过对比误差以及重构曲线,发现压力分布曲线与试验数据匹配完整,且精度较高,升力系数误差和俯仰力矩系数误差在0.005 以内。
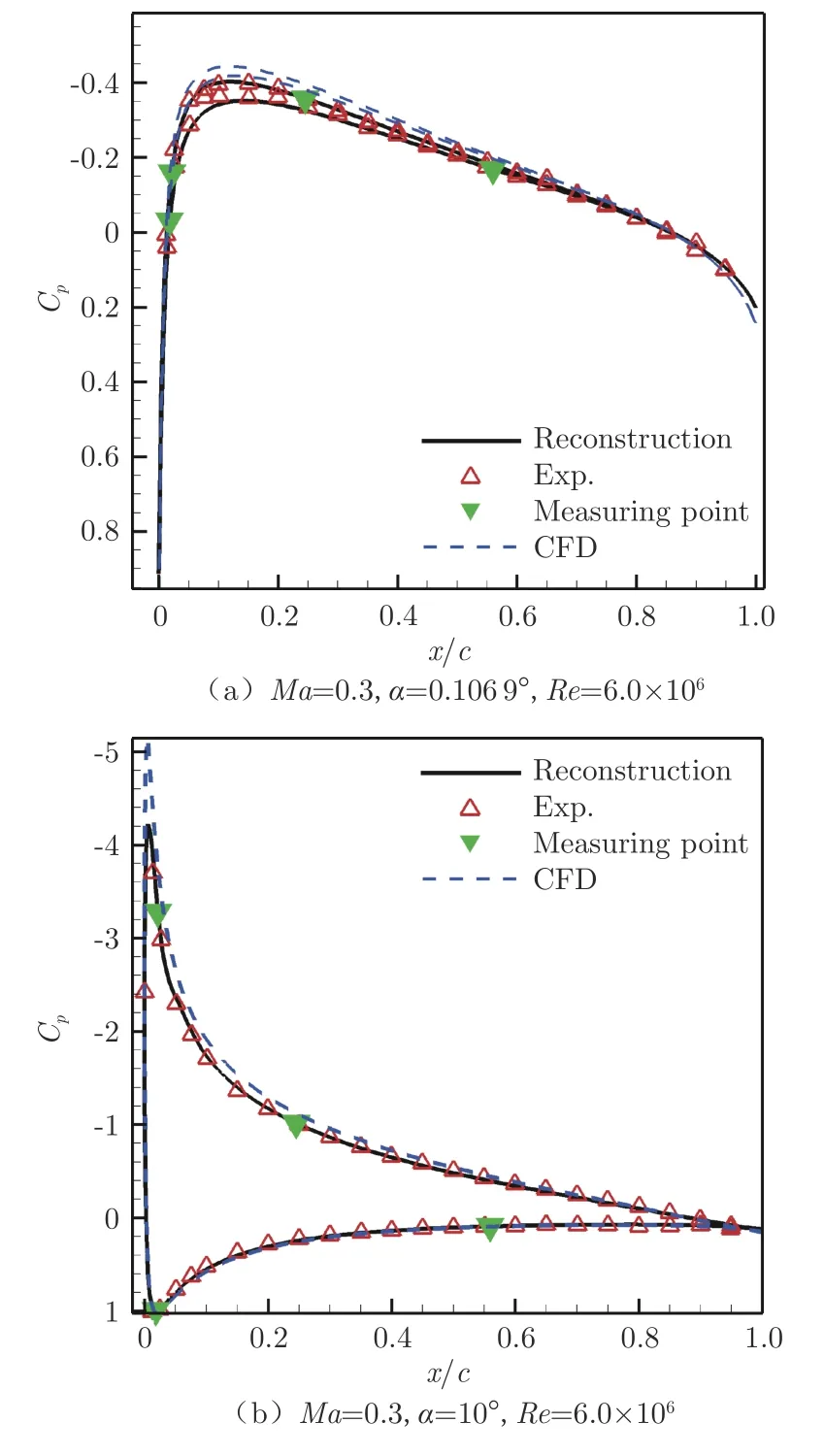
图4 NACA0012 亚声速重构结果Fig.4 Subsonic reconstruction results of NACA0012 airfoil
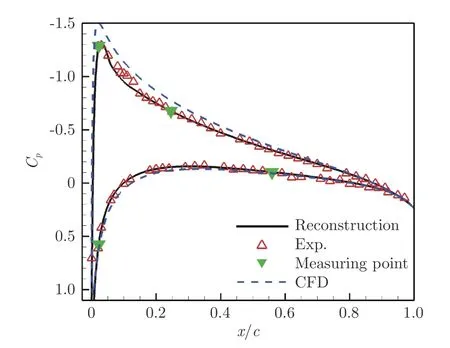
图5 NACA0012 亚声速重构结果Fig.5 Subsonic reconstruction results of NACA0012 airfoil
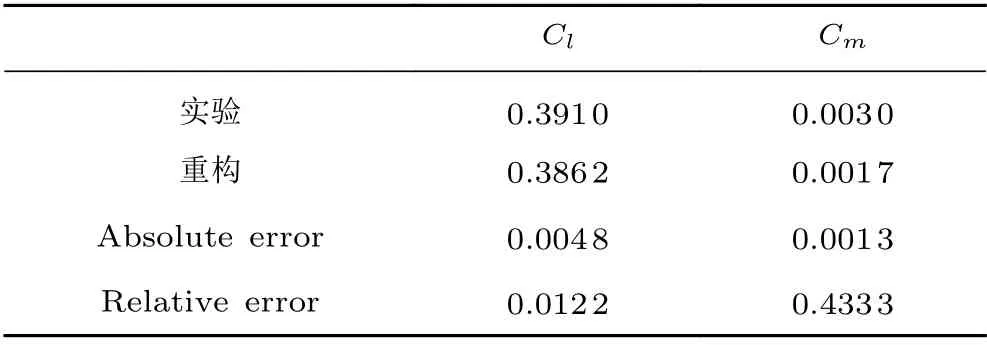
表1 重构误差Table 1 Reconstruction error
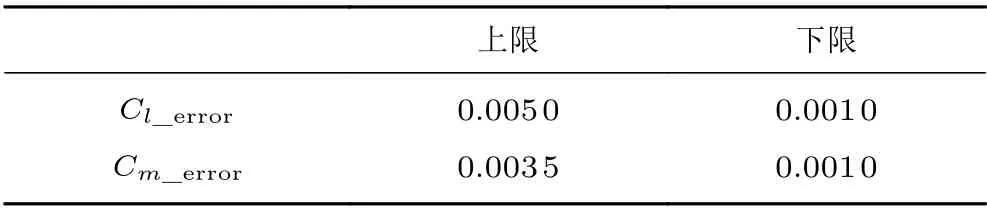
表2 误差区间Table 2 Error interval
图6为基于稀疏试验数据重构和传统插值方法重构的结果对比,其中试验数据与图5相同。图6(a)为翼型表面测压数据均匀采样结果,图6(b)为升力系数和俯仰力矩系数精度随试验点数量的变化曲线。图中,1–Error=1–|Intergral–Exp|,Integral表示积分获得的升力系数或俯仰力矩系数,Exp 表示升力系数或俯仰力矩系数的试验数据;绿线表示俯仰力矩系数精度,黑线表示升力系数精度,蓝色圆圈和红色菱形分别表示基于4 个试验点重构获得的压力分布积分得到的升力系数和俯仰力矩系数精度。如图6(b)所示, 22 个试验点重构误差的原因在于:其压力采样点位置没有选到吸力峰位置,导致积分误差较大,说明压力采样点位置的选取会影响插值重构方法的精度。可以看到,相比于传统插值重构方法,本文重构方法以稀疏的试验数据获得了高精度的升力系数和俯仰力矩系数。

图6 稀疏重构与插值重构结果对比Fig.6 Comparison of sparse reconstruction and interpolation reconstruction
2.2 跨声速流动
采用CFD 计算了100 组NACA0012 翼型跨声速状态的压力分布数据(Ma=0.6~0.8,=0°~4°),通过本征正交分解技术提取了14 组CFD 计算数据的POD 基函数。为了更好地捕捉激波特性,选取了14 个试验测压点处的数据进行重构。
图7为NACA0012 翼型在 Ma=0.652、=5.86°、Re=3.0×10和Ma=0.697、=4.86°、 Re=3.0×10这2种工况下的重构结果及其与试验和CFD 数据的对比,表3为CFD 计算、试验和重构得到的升力系数及对应误差。图8为NACA0012 翼型在Ma=0.756、=3.99°、Re=3.76×10,Ma=0.754、=2.98°、Re=3.80×10和Ma=0.754、=0.99°、 Re=3.96×10这3 种工况的重构结果及其与试验和CFD 数据的对比,表4为试验及重构的升力系数、俯仰力矩系数及其对应误差。可以看到,俯仰力矩系数相对误差较大。一方面,由于俯仰力矩系数积分点位于1/4弦线处,该点与气动中心距离较近,所以俯仰力矩系数值较小,导致其相对误差较大;另一方面,俯仰力矩系数不仅与压力分布相关,还与摩擦力分布相关,这可能导致相对误差较大。表5为较多试验工况下重构升力系数和俯仰力矩系数绝对误差上下限的统计结果。可以看出,即使CFD 计算结果与试验数据误差较大,但经过重构得到的压力分布曲线与试验数据吻合较好,能够获得与真实试验最完整匹配的压力分布曲线,且对激波站位捕捉较好。通过误差对比,能够将升力系数误差控制在0.005 以内,俯仰力矩系数误差控制在0.006 以内。
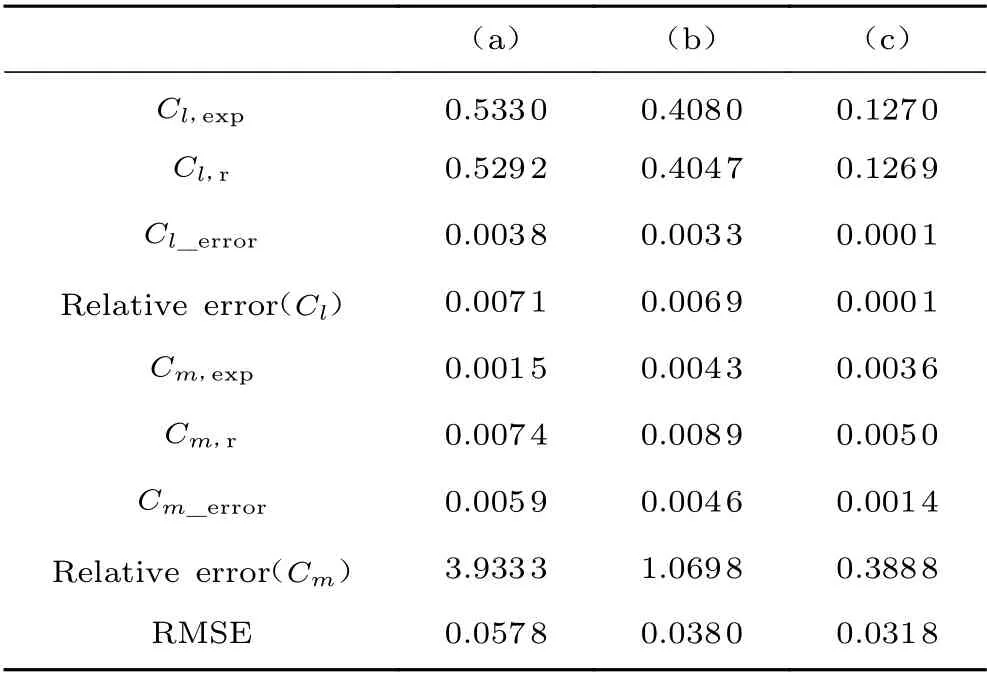
表4 重构误差Table 4 Reconstruction error
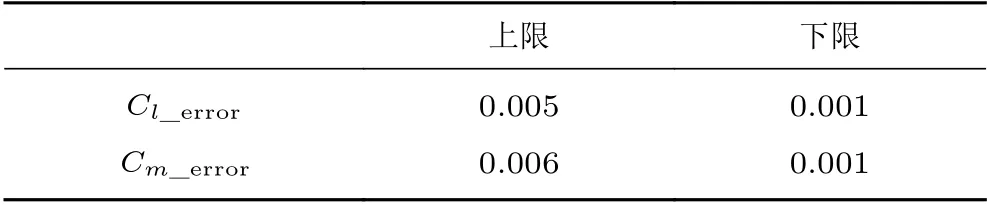
表5 误差区间Table 5 Error interval
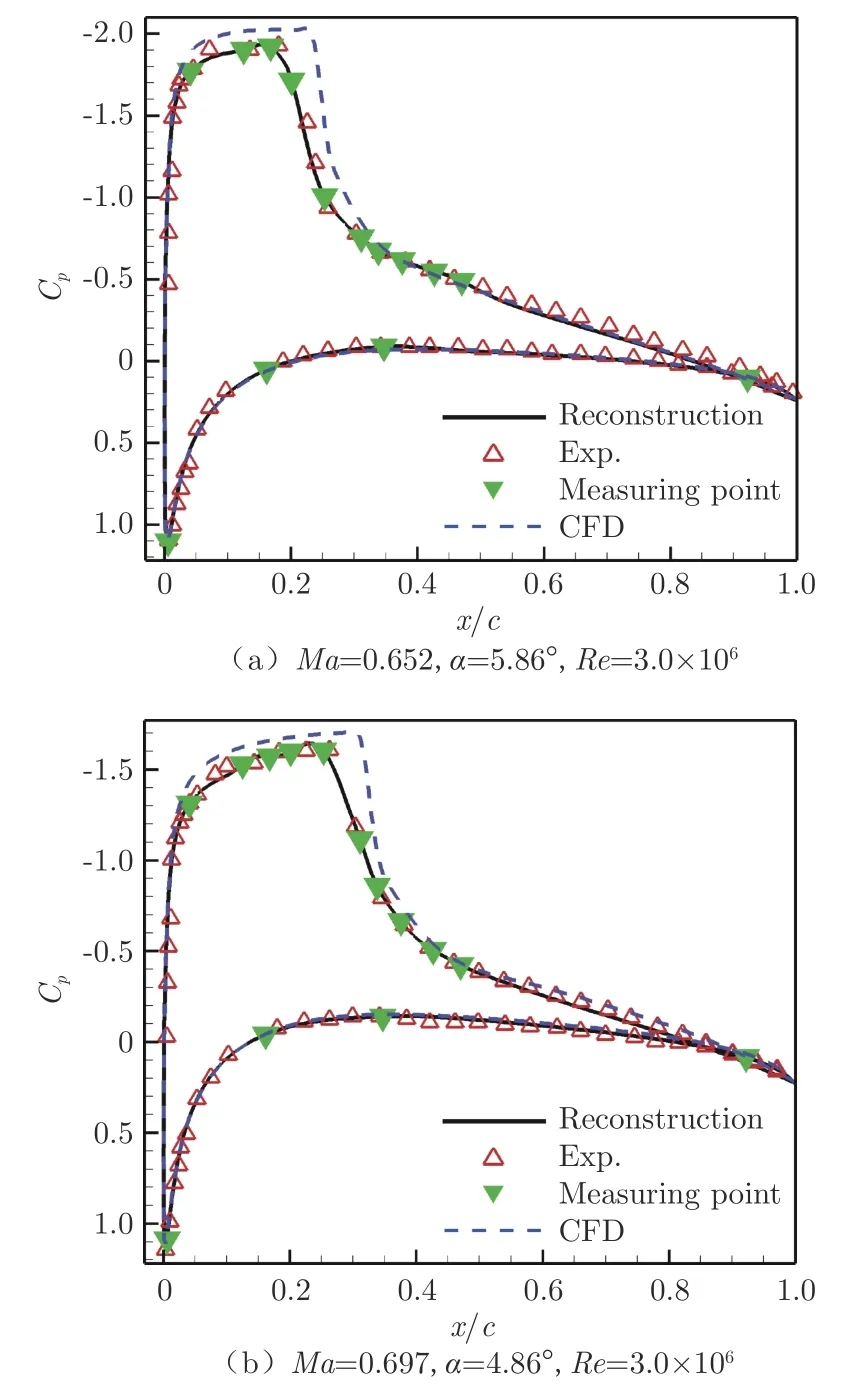
图7 NACA0012 翼型跨声速重构结果Fig.7 Transonic reconstruction results of NACA0012 airfoil

图8 NACA0012 翼型跨声速重构结果Fig.8 Transonic reconstruction results of NACA0012 airfoil
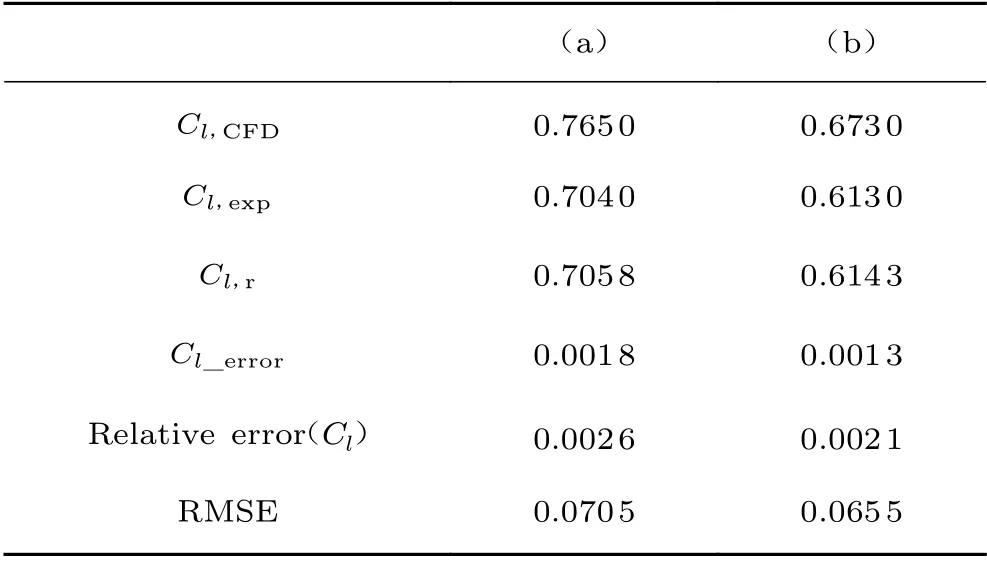
表3 重构误差Table 3 Reconstruction error
2.3 变几何变来流状态
本文采用CST 参数化方法,选用12 个CST 参数描述翼型表面几何形状,采用拉丁超立方抽样,在NACA0012 翼型CST 参数的1±30%范围内进行扰动,随机抽取样本翼型(所有样本翼型都与NACA0012 翼型不同)。采用CFD 计算了900 组压力分布数据,来流状态范围为Ma=0.6~0.75、=0°~4°。采用本征正交分解技术提取了20 组CFD 计算数据的POD 基函数,选取了18 个试验测压点处的数据进行重构。
为了证明本文发展的方法对于不同翼型仍然具有很好的泛化性,对3 种翼型进行测试,如图9所示,其中黑色点画线表示NACA0012 翼型,红色虚线表示MBB-A3 翼型,橙色实线表示RAE2822 翼型,浅蓝色线条表示通过CST 参数化随机采样获得的样本翼型。针对不同翼型表面选取测压点,首先将其横坐标归一化在[0,1]之间,然后根据之前所得18 个测压点位置,布点获得对应点的压力数据。

图9 翼型采样空间Fig.9 The airfoil sampling space
图10 为MBB-A3 翼型(Ma=0.698、=5.49°、Re=6.17×10工况)、NACA0012 翼型(Ma=0.753、=1.95°、Re=3.3×10工况)和RAE2822 翼型(Ma=0.676、=2.4°、Re=5.7×10工况)的重构结果及其与试验数据的对比,表6为试验和重构的升力系数、俯仰力矩系数以及对应误差。通过3 种翼型测试算例可知,与试验压力分布曲线相比,重构曲线存在小幅振荡。原因可能有两方面:一方面,由于CFD 计算样本量太少,提取的低维特征不足以完全捕获任意翼型在不同来流状态下压力分布所构成的特征空间;另一方面,提取的低维特征中存在高阶POD 基函数使其存在微小振荡。基于重构的压力分布曲线积分获得的升力系数和俯仰力矩系数仍满足要求,该方法针对变几何变来流状态算例仍然适用,但需要更多的POD 基函数和测压点数据。表7为较多试验工况下重构升力系数和俯仰力矩系数绝对误差上下限的统计结果,通过误差对比,能够将升力系数和俯仰力矩系数误差控制在0.005 以内。
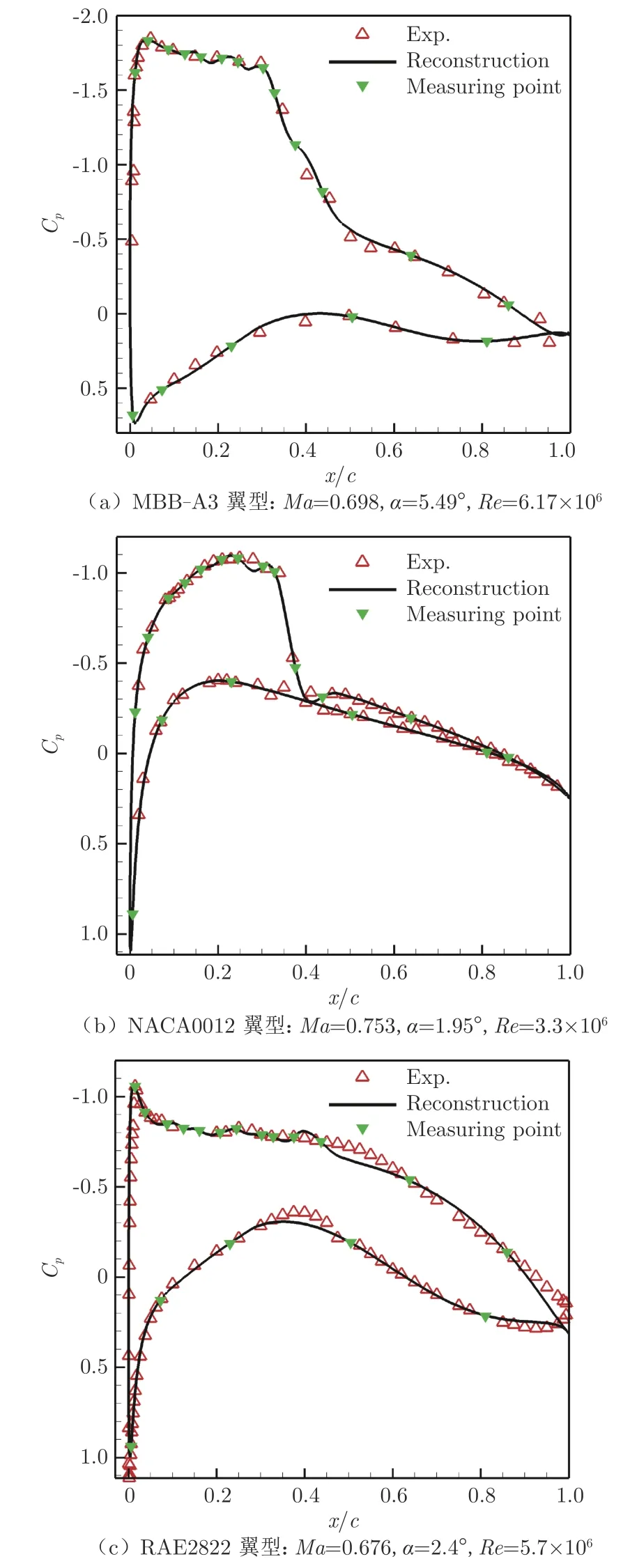
图10 变几何变来流状态重构结果Fig.10 Reconstruction of variable geometry with variable flow state
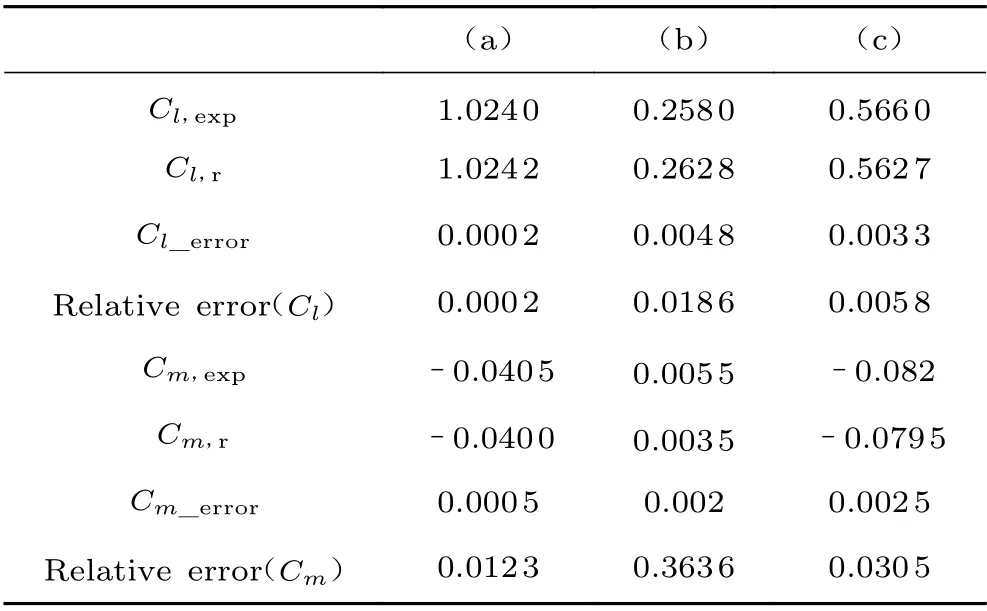
表6 重构误差Table 6 Reconstruction error
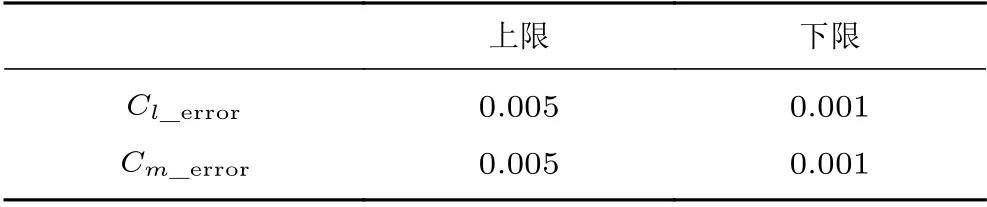
表7 误差区间Table 7 Error interval
3 结 论
本文提出了一种融合风洞试验数据和数值计算数据的新方法,基于较少的试验数据重构获得与真实试验最完整匹配的压力分布曲线。所发展的重构方法可在一定程度上解决空间受限稀疏观测条件下的分布载荷精细化重构难题。主要结论如下:
1) 通过提取压力分布CFD 计算数据的低维特征,利用有限试验压力测量数据获得的升力系数和俯仰力矩系数比直接通过试验数据积分获得的精度更高。
2) 该方法在固定翼型亚声速、跨声速算例以及变几何变来流状态算例中得到了验证,对不同翼型具有良好的泛化性,重构得到的分布载荷、升力系数和俯仰力矩系数均能精确匹配试验结果。
3) 由于跨声速区激波非线性的影响,需要更多的基函数和测压点来进行压力分布重构。
本文虽然是对压力分布进行重构,但提出的基于稀疏试验数据的融合方法可应用于剪应力和气动热测量等领域,对于其他学科也具有应用价值。
