基于CE/SE 方法对模块装药点传火过程的数值模拟及特性研究
2022-07-13森思义陶如意
森思义,王 浩,陶如意
(南京理工大学能源与动力工程学院,江苏 南京 210094)
1 引言
模块装药是一种用单元容器装填火药并分装式填进炮膛的装药方式,每一个模块单元都包含传火管与装药药筒。相较于其他装药方式,模块装药具有如下特点:便于进行药量组合并且便于变化药号,可以实现装药的自动化装填、提高火炮的应急能力,减少了火炮发射的机械动作,从而提高了火炮的可靠性,目前模块化装药方式已经在自行火炮中被广泛采用[1]。
模块装药作为目前内弹道领域的一个重要的研究方向,由于其装药结构的复杂性,其内弹道过程十分复杂,近年来研究者们针对这种装药方式,进行了诸多数值计算方向上的研究,如陆忠兵和周彦煌[2]针对模块装药的内弹道过程,考虑了模块间的隔仓区以及模块外的环形区,对各个区域建立了不同的计算模型并进行了数值仿真,数值结果表明受隔仓影响,膛内过程中形成了火焰传播的隔离带,各模块主装药区存在逐级燃烧的现象,轴向压力分布在隔仓区形成了明显的落差。赵毅[3]对模块装药的点传火过程进行了研究,其建立了传火管的一维两相流模型,对模块主装药区则采用集总参量法进行仿真,研究发现由于可燃传火管强度较低,传火管很早就会发生破碎并造成局部点火的现象。马昌军[4]针对模块装药的内弹道过程提出了一种新的计算模型,其建立了单独的膛内主装药床计算区域,模块破裂前对各个传火管及主装药区单独进行解算,破裂后各区域内的火药进行融合并在单独的主装药床上进行计算,数值结果表明模块间的阻隔效应影响了模块装药结构的传火性能,各模块不能同时破裂。
值得注意的是,大部分研究者对于这种装药方式的内弹道过程仿真均采用一维模型描述传火管,忽略了传火管燃气的径向效应;炮膛燃烧室内的自由空间采用集总参数法进行描述,忽略了模块端盖破裂后燃气在这一部分空间的发展过程。综上,为了深入研究模块装药内弹道过程中的多维特性,本研究主要针对单个模块的点传火过程,设计了一种金属装药模块并进行了点传火试验,构建了其点传火过程的二维轴对称两相流模型,采用CE/SE(The Method of Space-Time Conservation Element and Solution Element)方法对试验过程进行了数值仿真,并对仿真结果进行了详细分析。
2 实验部分
2.1 试验装置及相关试验参数
试验采用自制的金属模块药筒于燃烧装置内进行点传火试验,图1 为金属模块药筒及传感器转接装置示意图,其中药筒的半径和长度分别为50 mm 和153 mm,传火管的半径和长度分别为18 mm和153 mm,传火孔在空间上均匀分布,截面方向上为4 排孔,垂直于截面方向上为3 排孔,每排孔均各有2 个孔,孔径为2 mm;药筒上部以及燃烧试验装置均开孔,并配备传感器转接装置,以便传感器能够深入至筒内测量药筒内压力变化,具体如图1 所示,图2 为装配了金属药筒的燃烧模拟试验装置,表1 给出了不同区域的火药参数与装填密度。
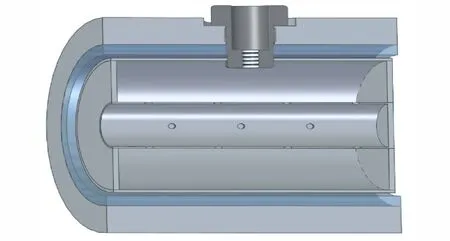
图1 金属模块药筒及测压装置示意图Fig.1 Schematic diagram of metal module cartridge and pressure measuring device

图2 燃烧试验装置Fig.2 Combustion device

表1 装药参数与装填密度Table 1 charge parameters and charge density
2.2 试验过程
试验通过数据采集仪与压电式压力传感器记录药筒内的压力变化,传感器型号为KISTLER-601H,其量程为0~100 MPa。药筒内传火管尾部封闭且传火孔无膜片,药筒及燃烧室尾部均有一层薄铝膜片,这种条件下的点传火过程为:点火头激发后产生底火流进传火管,靠近底火附近的黑火药优先被点燃,火焰及火药颗粒主要沿轴向朝尾部传播、扩散,其余黑火药逐渐被点燃,产生高温高压燃气并通过传火管上的传火孔流进药筒主装药区,点燃发射药,当药筒内主装药区压力达到膜片破膜条件时,膜片破裂,燃气及未燃完的火药颗粒流进燃烧室无火药的自由空间内,直到燃烧室膜片破裂,燃气与剩余火药颗粒开始外流,直至完全流出。
3 理论模型与数值计算方法
3.1 计算模型
本研究的模块药筒为一圆柱体,与燃烧室内壁存在大量不规则的狭窄间隙,且点传火过程主要发生在传火管、模块主装药区及燃烧室自由空间3 个区域,在尽量不影响计算结果的前提下,可只考虑上述3 个主要区域并忽略试验装置部分的复杂结构,对计算模型进行简化,其简化后的模型如图3 所示。
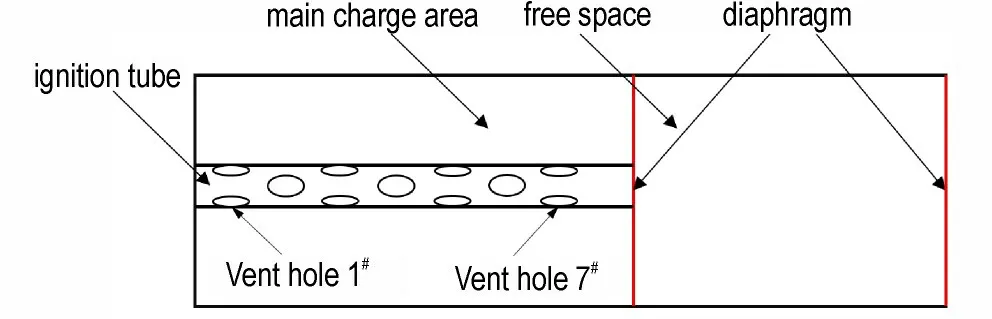
图3 计算模型示意图Fig.3 Schematic diagram of calculation model
值得注意的是,药筒和燃烧室尾部的膜片破裂过程实际上是一个复杂的流固耦合过程,为便于计算,提出一种假设,即它们的破裂完全是由内外压差导致,且达到破裂条件时膜片瞬时完全破碎,数值上表现为模块及燃烧室自由空间的膜片处壁面边界失效,模块与燃烧室之间变为自由流通的边界条件,燃烧室尾部变为流出边界条件;对于传火管,二维模型无法准确描述传火孔在周向上的空间分布以及孔的实际面积,在离散的传火管计算域内,孔所处位置均位于与模块主装药区相连接的边界处,显然二维轴对称模型下径向边界处的网格等效于三维模型下的最外环,因此需采用等效环模型处理传火孔,如图4 所示,即孔所处流出区的面积需满足ΔxΦ=Sh,这里Φ表示传火管的周长,Sh为传火孔面积,均为已知量,可求得Δx,以此推导出计算域传火孔处的网格尺寸。
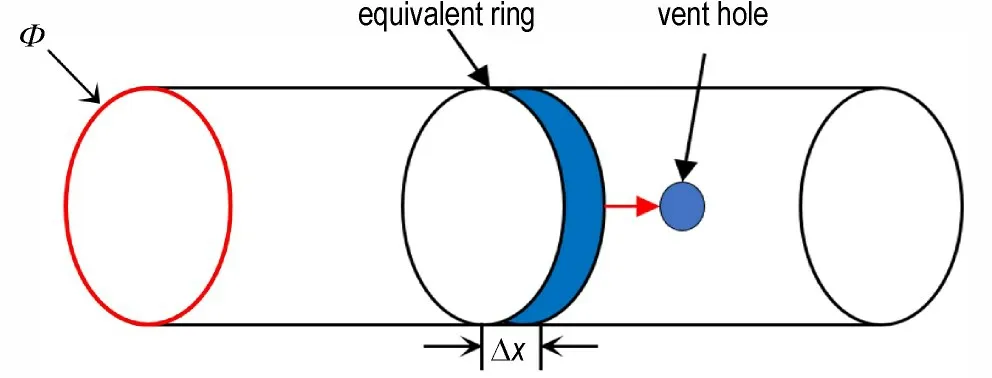
图4 传火孔等效环模型Fig.4 Equivalent ring model of vent hole
3.2 两相控制方程
针对试验过程,本研究建立了燃烧室内单模块装药条件下的二维两相流轴对称计算模型,整个计算域被划分为3 个区域,即传火管、模块主装药区以及燃烧室无火药的自由空间,计算设定条件如下:
(1)两相流模型采用双流体模型,即把火药颗粒作为具有连续介质特性的拟流体来处理;
(2)不考虑湍流的影响,忽略气体的黏性耗散以及壁面的热损失;
(3)固相颗粒是不可压缩的,即火药密度不变,所有药粒的尺寸均为当量尺寸;
(4)燃气服从Nobel-Abel 状态方程;
(5)火药燃烧服从几何燃烧和指数燃烧规律,火药一旦着火,其温度瞬间达到爆温。
3 个区域的两相控制方程均可用如下方程组描述[5]:
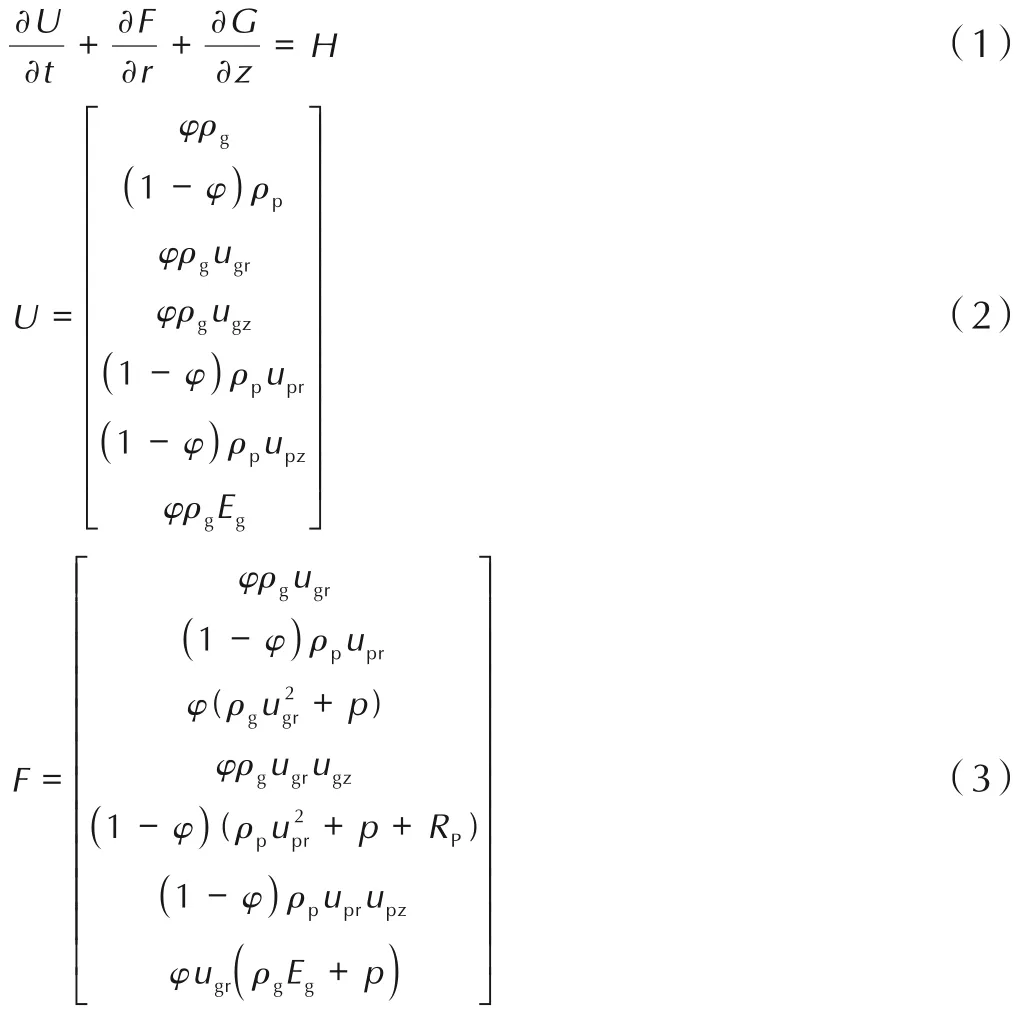
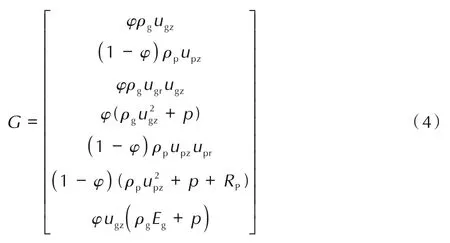
式中,径向通量F及轴向通量G均为守恒变量U的函数,φ为空隙率;ρg为气相密度、ρp为固相密度,kg·m-3;ugr和ugz分别为气相的径向速度和轴向速度,m·s-1;upr和upz是固相的径向速度和轴向速度,m·s-1;Eg为气相总能,J·kg-1。p为气相压强,Pa;Rp为颗粒间应力,Pa。
需要特别指出一点,对于不同的区域,源项H的表示方法是不同的,除传火管外,其余区域均不含与底火有关的项,而其它项的表示方法则相同,传火管的源项为:

式中,mc为单位时间单位体积内的燃气生成量,kg·s-1·m-3;Fsz和Fsr为两相间的轴向阻力和径向阻力,N·m-3;mig为底火源的燃气生成量,kg·s-1·m-3;ep为单位质量的火药化学潜能,J·kg-1;Hig为底火燃气流入的滞止焓,J·kg-1;Uigr和Uigz分别为底火燃气的径向速度和轴向速度,m·s-1;Qp为相间传热量,J·s-1·m-3。为构建封闭方程组,关于火药燃烧及相间作用的辅助方程主要参考文献[6]。
3.3 数值计算方法
对含有强间断现象的内弹道过程的数值模拟,所采用的数值计算方法必须在保持计算精度的前提下同时具备对间断的高效捕捉能力。本研究采用的CE/SE方法是一种计算守恒性方程的格式,其特点是同时考虑流场域空间与时间两个维度,统一划分成若干个网格,并将其分解为若干守恒元和解元,基于守恒元边界上空间通量与时间通量的守恒性构造出其差分格式。此格式构造简单、计算精度较高,并且对间断具有很强的分辨率,简单地引入权函数即可进行捕捉[7-8],避免了传统迎风格式用以处理间断的限制器可能导致的过度数值耗散。二阶CE/SE 计算格式的推导过程及其相关项的求解方法可参见文献[9],其在轴对称坐标系下的二维无粘反应流的计算格式为:
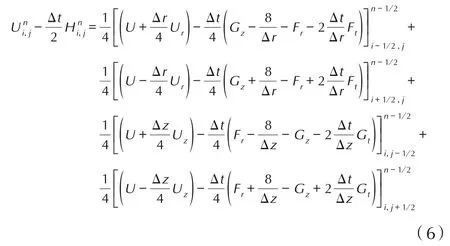
式中,i,j分别对应径向r和轴向z空间网格点的坐标,n为时间迭代步数,由于流场中存在强间断现象,Ur和Uz这两项需采用差分重构的方法进行求解[10],即:
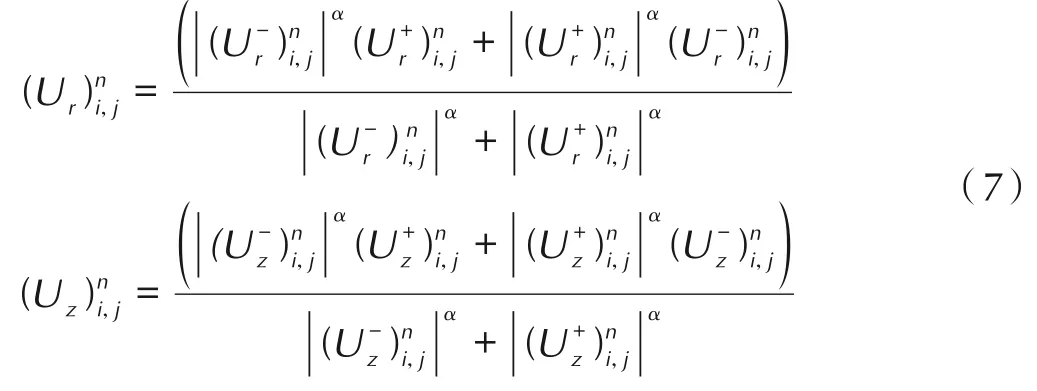
α为可调节常数,通常取1-2,本文中取2。
格式稳定性条件为:
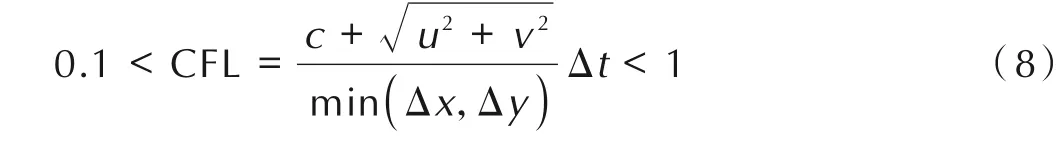
式(6)中所介绍的CE/SE 方法含有带火药燃烧反应的源项,相对于流场反应的特征时间,燃烧反应过程的时间尺度是较小的,直接求解式(6)可能会导致数值解的不收敛,所以这里采用分步求解的方法:对于任意时间步,在不考虑源项的 情 况 下 求 解 出,即求解不 含的式(6),再通过计算中间参量得到的值,最后采用四阶龙格库塔法求解常微分方程组dU/dT=H,即可得到下一时间步的。
3.4 边界条件与初始条件
本研究中计算域选择中心轴线以下的部分,对于各个计算域,其边界条件设置如下:
(1)轴对称边界条件:轴线上流体的速度沿法向的分量为零,其他物理量沿轴线法向方向上梯度为零。
(2)流通区域边界条件:对于各个计算域,未连通时边界条件设置成固壁条件,形成流通状态后,即破孔或破膜后,各个计算域相连通位置处的边界条件变为自由输入、输出边界,即边界处各物理量沿流动方向的梯度为零。
(3)固壁条件:无粘流动中,固壁边界设置成有滑移边界条件,气相与固相的速度沿法向的分量为零。
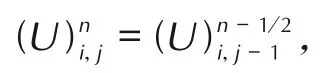
初始时刻,传火管与主装药区的空隙率由火药装填密度决定,燃烧室自由空间区空隙率为1,初始压力p0为0.1 MPa,气固两相初始速度均为0,初始温度T0为室温,初始气相密度为ρg0=p0(p0β+ RT0),其中β为火药气体余容,R 为火药气体的气体常数。
4 计算结果及分析
4.1 传火管点传火过程分析
图5 给出了不同时刻传火管内气相的压力与径向速度分布图,图6 给出了传火孔1 至孔7(分别对应底火端至传火管尾部的7 个传火孔)随时间的气相径向速度分布图。图5a 是点火初期的压力分布图,由于底火源是一种高强度的瞬态源,在点火初期流场中就形成了明显的轴向压力梯度。由图5b 可见,当传火管内黑火药被点燃后,伴随着传火孔处燃气的外流,轴向压力梯度整体不再明显,而传火孔周围则呈现了明显的径向压力梯度;黑火药颗粒药床主要受燃气轴向上的推动作用,逐渐向传火管尾部堆积,燃气经过颗粒密集区时会生成大量燃气,且伴随着局部燃气密度的增大,6.39 ms 左右时尾部处已形成了明显的高压区,波峰处约为12 MPa,随后压力波反射,如图5c~5d 所示,图5d 也给出了同一时期的气相密度分布图,显然高压区同时伴随着高气相密度。在整个点传火过程中,径向上的压力梯度推动了燃气的外流,气体朝着传火孔所处方向不断加速,从点火过程开始,传火管内压力不断升高,径向流速也在不断提高,随着燃气向药筒主装药区不断注入,主装药区的压力逐渐上升,管内外压差逐渐减小,使得在一段时间内传火孔处气体的径向流速趋于平缓,当压力波形成后,局部的高压高密度燃气会促使传火孔处气相径向流速的陡增,最大径向流速可达127 m·s-1,如图6 所示。
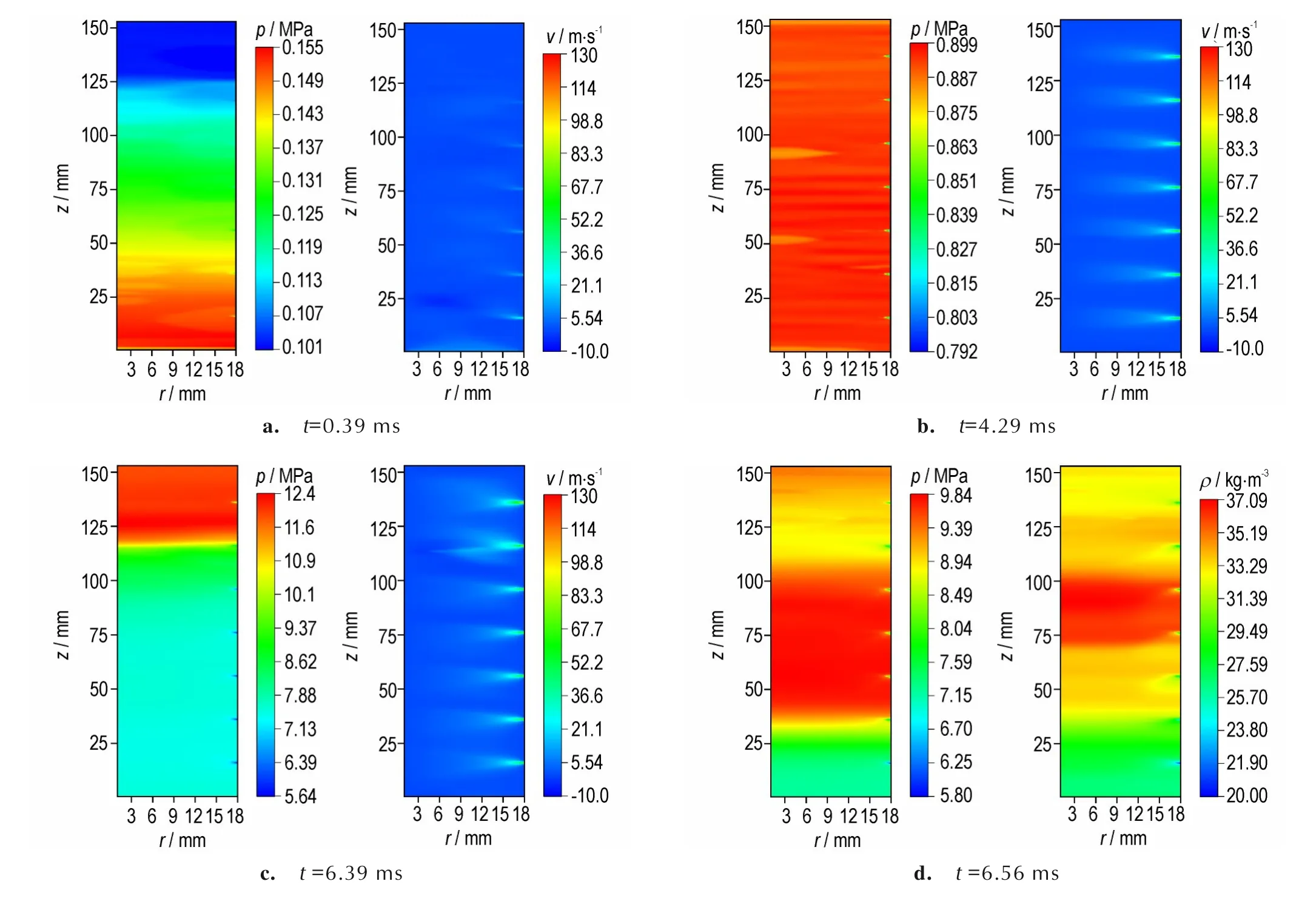
图5 不同时刻传火管内压力分布与气相径向速度分布图Fig.5 The distribution of pressure and gas radial velocity in ignition tube
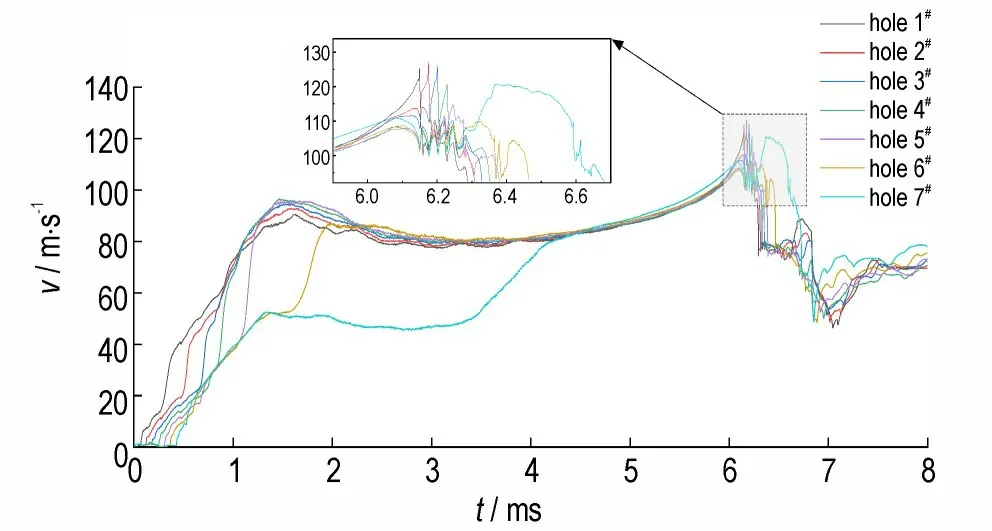
图6 传火孔处气相径向速度曲线Fig.6 The gas radial velocity of vent holes
4.2 主装药区火药燃烧过程分析
主装药区不同时刻的火药温度及压力分布如图7所示。图7a 还给出了初始时刻主装药区的空隙率分布,可见对于主装药区,当传火管燃气开始注入时,火药颗粒逐渐向边界处堆积,继而会导致初始时期径向上的压力落差;在相间传热的作用下,近传火孔处火药最先被点燃,火药一经点燃,随即达到爆温,如图7b 所示;由图7c 可以看出,在传火孔处燃气射流的作用下,由于气相的径向流动效应显著,燃气能量主要沿径向传播,火药也主要随径向被点燃。而随着火药的逐层点燃,除传火孔射流区域外,主装药区此时已无明显的径向压力梯度,压力分布整体显得较为平均;在整个点传火过程中,除燃气射流导致的火药燃烧,局部火药点燃后向外释放的大量化学能也促使了其余火药的燃烧,由图7d 可见大约在6.81ms 左右时整个主装药区的发射药几乎被完全点燃,此后主装药区压力上升幅度逐渐向峰值逼近;当主装药区的膜片破裂后,燃气的出流会导致出口处形成明显的轴向压力梯度,如图7e所示。图8 给出了主装药区测压点的圧力曲线的仿真值与试验值,计算所得最大压力为2.64 MPa,试验结果为2.66 MPa,计算所得结果与实验结果相比基本吻合。
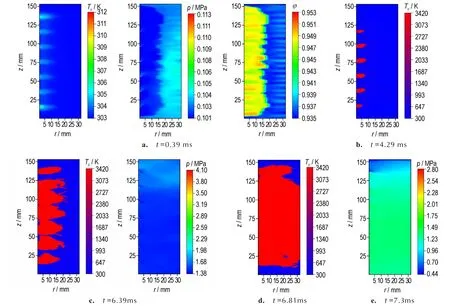
图7 不同时刻主装药区火药温度及压力分布图Fig.7 The distribution of pressure and propellant temperature in main charge area
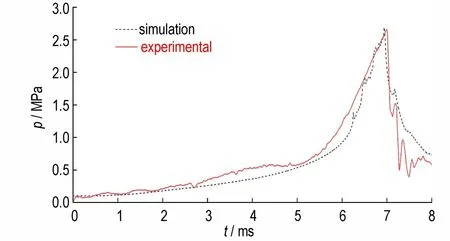
图8 测压点圧力曲线Fig.8 The pressure curves of simulation and experiment
4.3 燃烧室自由空间激波形成分析
图9 是破膜瞬间即主装药区膜片处达到破膜压力时,燃烧室自由空间的气相密度和马赫数分布图,可以明显的看出有一道激波在此时产生,这是由于相对于燃烧室无装药的自由空间,主装药区为一高压高密度区域,破膜瞬间高温高压燃气射流进入燃烧室自由空间,燃气的密度远高于自由空间内气体的密度,燃气向出口外膨胀,压缩波汇聚叠加,因此在燃气射流区域形成了明显的高密度区域,同时在射流的作用下,出口处的高马赫数区域随之形成。可以预见的是,模块装药结构的特殊性极易在膛内点传火过程中产生激波现象,典型如药筒内传火管的破孔过程,其破孔后的燃气射流同样会伴有激波形成,进而影响主装药区的升压过程,针对这一构想,4.4 节专门对一假设工况下(此工况下传火孔孔径设定为4 mm)3 种不同破孔压力的传火孔燃气射流过程进行了仿真分析。
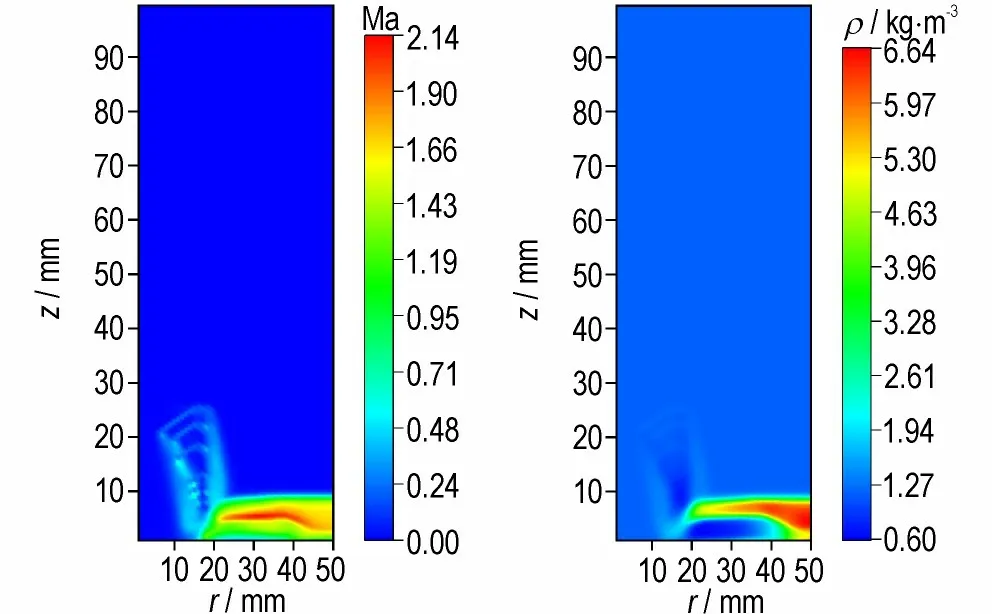
图9 破膜瞬间燃烧室自由空间马赫数与气相密度分布图Fig.9 The distribution of gas density and Mach number in free space of combustor at the moment of diaphragm breaking
4.4 传火孔破孔过程的仿真及分析
图10 给出了破孔压力为3 MPa 时不同时刻主装药区的气相马赫数分布图和速度矢量图。显然传火管内压力的分步不均会导致破孔明显存在时序上的差异;破孔后的主装药区形成了向四周扩散的激波,这与文献[12]所讨论的传火孔射流激波现象基本接近。当传火通道形成后,燃气在狭窄的区域内向外释放,且主要沿径向方向流动,如图10a 所示。受激波影响,传火孔出口位置的气相流速接近音速,大约在离轴线1 mm 的位置处便形成了明显的超音速流域,燃气经传火孔向外传播,并主要沿径向方向上扩散,破孔初期气相的径向流速在马赫数最大区域约为502 m·s-1,之后不断加速,在3.33 ms时达到了729 m·s-1,如图10b~10c 所示,相较于无膜片的情况,气相流速显著增大。图11 给出了不同破孔压力下主装药区某网格点的压力随时间变化的曲线图,对比可知,传火孔无膜片的主装药区升压过程中的压力曲线较平滑,但当存在破孔条件时,气相径向流速的增大会显著提高传火孔燃气射流的流量,因此主装药区压力上升的趋势更为剧烈且伴有明显的震荡。
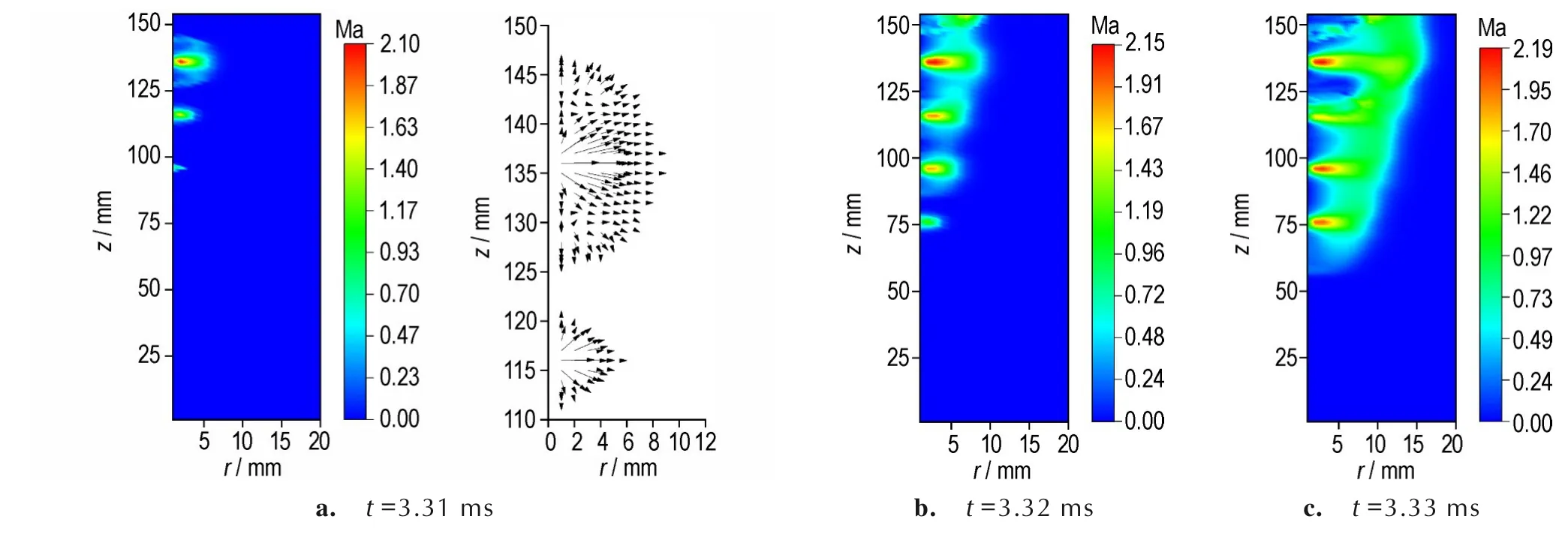
图10 不同时刻主装药区气相马赫数与速度矢量分布图Fig.10 The distribution of gas Mach number and velocity vector in main charge area
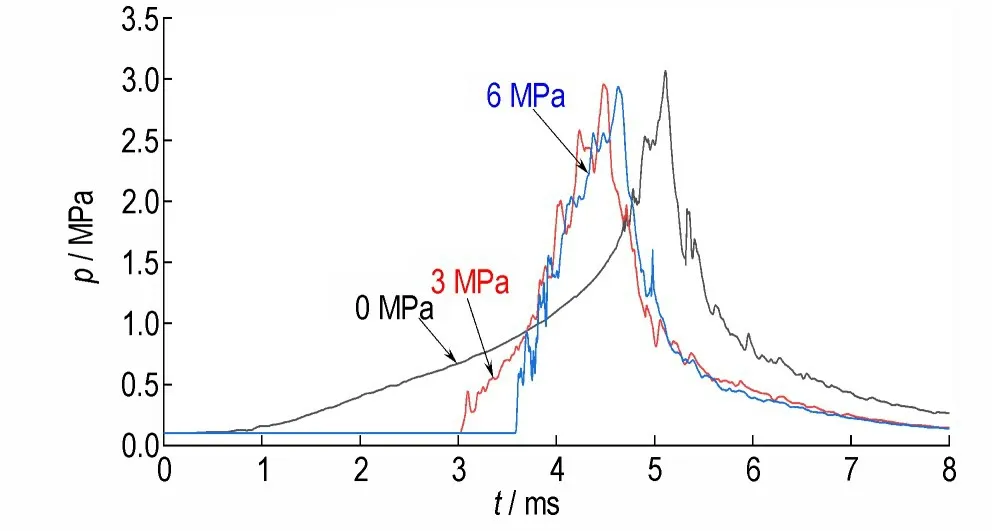
图11 不同破孔压力下主装药区测压点的压力曲线Fig.11 Pressure curves of a pressure measuring point in main charge area under different breaking pressure of vent holes
5 结论
基于模块装药条件下的点传火试验,建立了试验条件下的计算模型并采用CE/SE 方法进行了数值仿真,通过试验结果与计算结果的对比,验证了模型的准确性,所建立的模型能较准确的描述试验过程。揭示了模块药筒传火管的传火与破孔规律、主装药区火药着火规律和升压规律,以及点传火过程中的激波形成现象。主要结论如下:
(1)对于传火管,点火初期轴向上存在着较大的压力梯度,之后逐渐平缓直至压力波形成,伴随着传火孔处燃气向管外的流出,传火孔区域会逐渐形成较为明显的径向压力梯度;整个点传火过程中气相的径向流动效应十分明显,其径向流速受管内外压差影响呈现增减的趋势。
(2)受燃气射流的径向传播影响,主装药区发射药主要沿径向方向被点燃;传火初期,火药颗粒受径向上的推动作用会逐渐堆积在边界处,此时会形成较为明显的径向压力落差,随着火药的逐层点燃,径向上的压力落差消失;当膜片破裂后,燃气的轴向外流会导致出口处形成明显的轴向压力梯度。
(3)药筒的膜片破裂后,主装药区燃气射流进入无火药的燃烧室自由空间,燃气射流区会发生明显的激波现象,形成局部的高密度、高马赫数分布。
(4)对假设工况下的传火孔破孔的射流过程进行了研究,传火孔的破孔具有不一致性;传火孔破孔后会导致激波在孔外产生,并向四周扩散。受激波影响,气相流速显著提高,进而导致主装药区在升压过程中的压力震荡十分明显且升压幅度相较于传火孔无膜片的情况下更为剧烈。
