拉伸载荷下PBX-9501 裂纹产生的数值模拟

何各燚，刘占芳，2，段连龙

（1. 重庆大学 航空航天学院，重庆 400044；2. 非均质材料力学重庆市重点实验室，重庆 400044）

1 引言

PBX 材料中占极大体积分数的单质炸药颗粒（通常可达90%以上）与高聚物黏结剂之间存在相互作用，力学响应较为复杂，从宏观角度准确描述PBX 材料的性质和力学行为特征较为困难，因此采用细观结构表征技术以及与宏观力学性能相关联的研究方法是非常有效的研究手段［1］。PBX 所具有的含能敏感特性给力学性能的实验研究带来了困难，通过数值模拟方法来研究炸药的力学性能越来越受到人们的重视，如何建立符合实际PBX 材料的细观结构模型是进行数值模拟的关键。

国内外对PBX 细观结构的几何建模研究主要是通过建立以材料细观结构为基础的数值模型［2-3］，证明二维代表体积元方法的有效性［4-5］，这在一定程度上较好地预测了炸药颗粒的性质、体积分数、形状和级配以及黏结剂的性质等对有效弹性模量的影响［6-7］。为了建立合适的PBX 细观模型，许多研究者通过数字图像处理技术手动建立材料模型。Arora 等［8］通过对显微电子图像中不同相的识别建立了PBX 细观结构模型，Manner 等［9］利用X 射线对HMX-HTPB 基的PBX 炸药进行扫描，并在此基础上建立了PBX 细观结构模型，但此方法需要昂贵的设备和时间成本。韦兴文等［10］尝试利用随机投放方法建立PBX 随机圆形颗粒模型，然而这种方法很难使炸药颗粒体积分数达到85%及以上。戴开达等［6］为了提高PBX 细观模型中炸药颗粒的体积分数，以规则的多边形炸药颗粒来替代圆形的炸药颗粒，但颗粒的不规则性以及随机分布性却无法保证。Guo 等［11-13］采用Voronoi 方法建立了PBX 细观模型，此时Thiessen 多边形颗粒能够保证随机分布和体积分数的要求，但生成的颗粒尺寸过于均匀。康歌等［14-17］利用随机模拟方法，在给定区域随机生成多种类型的圆形颗粒，再由各圆心生成Voronoi 图建立PBX 细观模型，该模型不仅能够反映级配，且能达到较高的颗粒体积分数，然而由大圆周围的小圆生成有规律的条状散射形状的Thiessen 多边形，以及由大圆生成的Thiessen 多边形面积明显变小，因此仍需要对模型进行修正。

大量的实验结果表明，在拉伸载荷作用下，PBX 的主要损伤形式为界面脱粘［19］，PBX 在拉伸下的断裂行为受到晶体间界面性质的显著影响［20］，但是界面属性很难描述。大多数研究是基于牵引力和开口位移之间关系为线性这一假设［21-22］，其中Tan［23］使用数字图像相关方法获得内聚力规律，并提出了三阶段黏结界面本构关系。

相较于三维模型，对二维模型进行数值模拟能够得到更加直观的结果并减少大量的计算量，得到的结果也具有一定的可靠性。用二维的平面模型来表征三维的实体结构时，通常是参考三维实体的截面几何分布，但值得注意的是二维截面并不一定是三维颗粒的最大截面，即截面中的颗粒面积大小并不能表征颗粒体积的大小。因此本研究将通过随机生成三级配圆，并采用大级配最大化方法，以达到所有圆面积总和最大化的目的，这与PBX 压制工艺中采用级配以增加颗粒体积比的思想相一致。本研究基于Voronoi 方法，对于PBX 细观几何结构上的建模进行改进，建立更加符合实际的不同级配下晶粒分布的二维几何模型。在此基础上建立二维代表体积元，采用三阶段黏结界面损伤本构关系，对含有细观结构的PBX-9501 进行静态拉伸下的界面脱粘数值模拟，研究静态拉伸下颗粒与黏结剂界面力学行为。

2 具有细观结构特征的PBX 几何建模

2.1 PBX 几何建模布种

运用随机模拟方法，在给定区域生成3 种类型的圆形颗粒，将所有圆称为种子，圆半径称为种子大小。每个种子除了位置坐标信息外，还有种子大小的信息。

运用Matlab 软件，首先在S=1 mm×1 mm 区域内随机产生N=106个点，由随机产生的点为圆心，以半径为r1=50 μm 依次作圆，后产生的圆与之前的圆不能相交，且与之前产生的圆中至少存在一个满足（1）式关系：

式中，L为两圆之间的距离，r为存在的圆的半径，δ1为控制参数，本研究中取值为2，遍历所有的随机点。同理逐次产生r2=12.5 μm，r3=3 μm 的圆（控制参数同样取2），分别在S区域内生成大种子79 个，中种子379个，小种子3534 个，如图1 所示。

图1 三级配颗粒逐步布种Fig.1 Seed distribution of three graded particles gradually

2.2 生成Voronoi 模型

由种子位置信息生成Voronoi 图，在Matlab 软件中生成CAD 命令流文件，并将每一个Thiessen 多边形缩放形成黏结剂层，缩放为向内偏移m/2=0.5 μm，生成黏结剂厚度m=1 μm 的模型，如图2 所示。由于颗粒采用的是三级配，而且Voronoi 方法生成的模型只用到了种子的位置信息，所以明显可观测到由大种子生成的Thiessen 多边形面积偏小，由大种子周围的小种子生成Thiessen 多边形成条状的散射状。

2.3 改进的几何模型

Thiessen 多边形的每个顶点对应Delaunay 三角形的外心［18］，是由3 个种子的位置信息确定。如图3所示，图3a 中O点为修改前的顶点位置，图3b 中O点为修改后的顶点位置，将每个顶点的位置进行修改，加入种子大小的信息，为了保证所得顶点仍然在三角形内部，并且顶点位置更加偏向小种子，采用面积加权来重新确定多边形的顶点位置O，使得顶点与三角形组成的3 个三角形的面积之间满足（2）式：

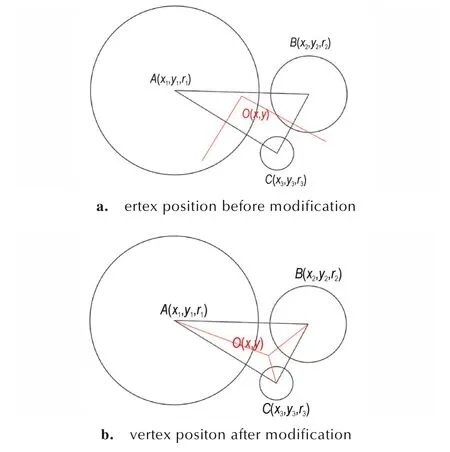
图3 在Delaunay 三角形中重新生成多边形顶点Fig.3 Regenerating polygon points in Delaunay triangles

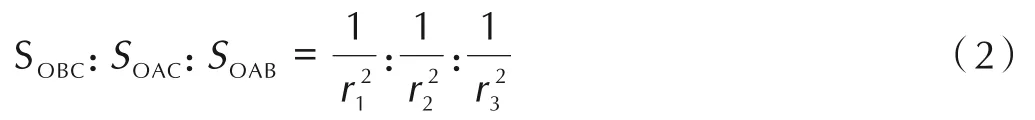
则可得顶点坐标为：

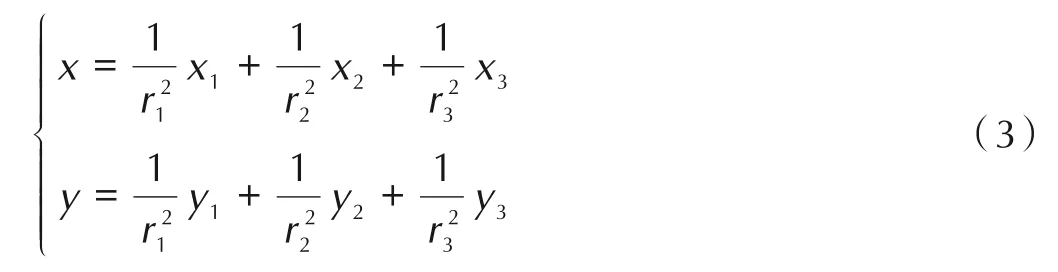
由修改后的多边形同样缩放形成黏结剂层，缩放为向内偏移m/2=0.5 μm，生成黏结剂厚度m=1 μm的模型，如图4 所示，模型颗粒面积分数为90.5%，黏结剂面积分数为9.5%。改进后的模型与种子的契合度明显提升，颗粒为三级配时比Voronoi 图模型更加符合PBX 实际细观结构，但仍存在大颗粒多边形趋于圆形的缺点。模型的颗粒分布如图5 所示，其中图5a为不同面积颗粒数量分布，图5b 为不同面积的颗粒面积分布，从中可以得出模型具有小颗粒数量多、大颗粒与小颗粒面积占比相当、中颗粒面积占比最少的特征。

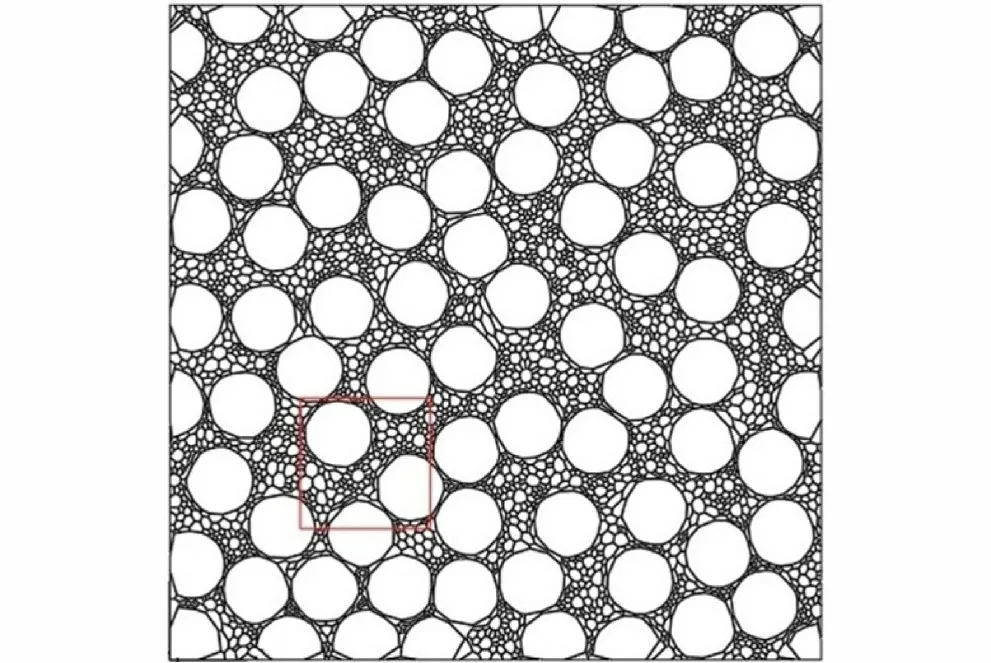
图4 改进后的模型Fig.4 Improved model

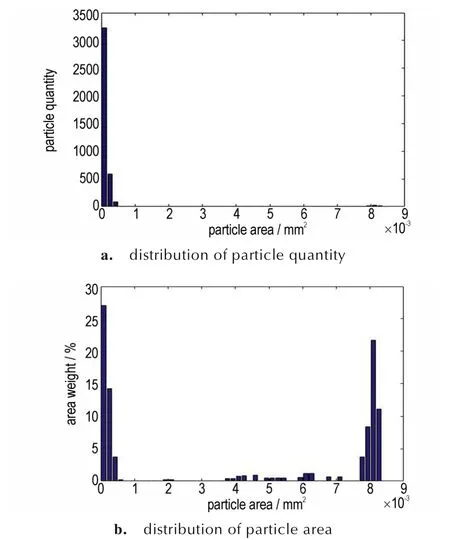
图5 模型中的颗粒分布Fig.5 Particle distribution in model

3 PBX-9501 静态拉伸下的界面脱粘数值模拟

3.1 有限元单元划分

采用有限元方法模拟PBX-9501 在准静态拉伸下的断裂行为，所有仿真均在Abaqus 软件中实现。选取模型中区域0.2 mm×0.2 mm（图4 中的红色区域），生成草图导入Abaqus 建立几何模型，并作为PBX-9501周期性边界条件代表体积元，如图6 所示。

图6 在Abaqus 中建立模型Fig.6 Modeling in Abaqus

网格和加载边界如图7 所示。颗粒与黏结剂实体均采用三角形平面应变单元，约有11000 个。在黏结剂内部及颗粒与黏结剂界面插入黏结面单元，约有7000 个。左边界固定x方向位移，下边界固定y方向位移，在上边界加载y方向位移。

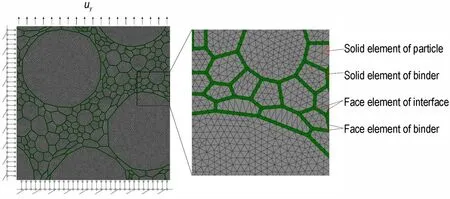
图7 约束与载荷边界条件及网格划分Fig.7 Boundary conditions and meshing

3.2 颗粒与黏结剂界面的本构模型

大量实验结果表明，在拉伸载荷作用下，PBX 的主要损伤形式为界面脱粘。PBX-9501 在拉伸下的细观裂纹路径如图8 所示。由图8 可见，在拉伸载荷作用下PBX-9501 明显存在一条主裂纹路径，裂纹主要沿颗粒的边缘扩展［19］。

图8 拉伸载荷下PBX-9501 的微观裂纹路径［19］Fig.8 The microscopic crack path of PBX-9501 under tensile loading［19］

PBX 在拉伸下的断裂行为受到晶体间界面性质的显著影响［20］，但是界面属性很难描述。大多数研究假设牵引力和开口位移之间的关系是线性的［21-22］，Tan［23］使用数字图像相关方法获得内聚力规律，并提出了一个解析表达式。该表达式有3 个参数：黏合强度最大值、刚度和退化刚度

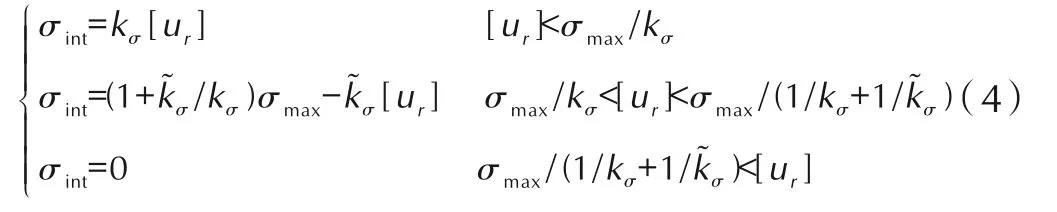
式中，σint为界面法线应力，ur为开口位移。如图9 所示，该关系由3 个线性阶段组成。

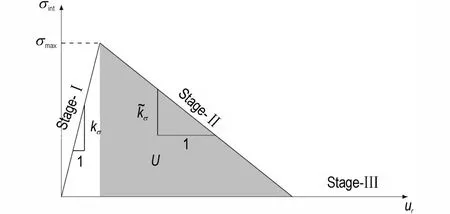
图9 界面法向力与张开位移的关系Fig.9 The relationship between the normal stress and the opening displacement of interface

在数值模拟中，由弹性实体单元与黏结面单元共同描述黏结剂力学行为，其中弹性实体单元描述第一阶段，黏结面单元描述第二、三阶段，如图10 所示。

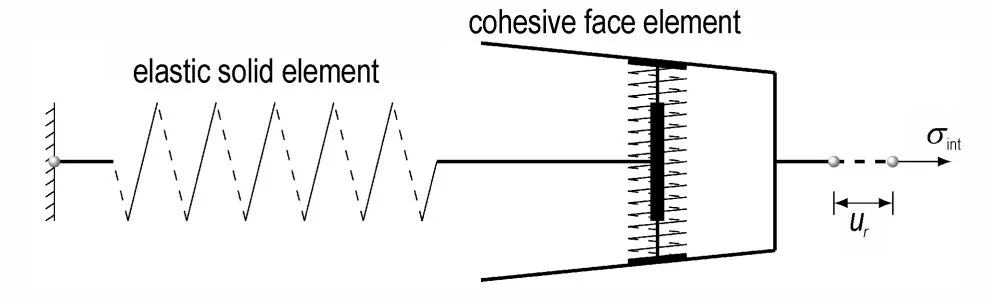
图10 黏结剂层本构关系示意图Fig.10 Diagram of the constitutive of the binder layer

切向应力与切向位移的关系与法向关系相同。参考文献［24］中的参数选取，界面黏结强度为1.66 MPa，刚度为1.55 GPa·μm-1，退化刚度为17 MPa·mm-1；黏结剂假定为线弹性，弹性模量为1 MPa，泊松比为0.499；晶体颗粒假定为线弹性，弹性模量为30 GPa，泊松比为0.322。

4 结果与讨论

本研究通过随机生成三级配圆，并采用大级配最大化方法，建立了不同级配下晶粒分布的二维几何模型，采用三阶段黏结界面损伤本构关系及有限元方法模拟了PBX-9501 在准静态拉伸条件下无初始损伤模型的断裂过程。为了验证模拟的有效性，将模拟得到的拉应力应变关系结果在图11 中用实线表示，将文献［25］中PBX-9501 巴西圆盘实验数据在图11 中用虚线表示，对比表明：在数值模拟与实验中具有几乎相同的拉伸强度和初始刚度，但在数值模拟中明显存在一个较大的刚度退化阶段，而实验结果的刚度退化不明显；在数值模拟结果中曲线末端出现波动，但实验曲线只有上升阶段而无下降阶段。分析产生差异的原因：一是因为数值模拟的对象为代表性体积单元，尺寸小，单个微裂纹的产生对整个材料影响大，而实验对象的尺寸很大，单个微裂纹的产生对整个材料影响小，所以在数值模拟中出现波动，而实验中波动不明显；二是采用静态加载方式，数值模拟出现下降段是因为在该阶段有静态稳定解，实验无下降段是因为在该阶段无静态稳定解，裂纹产生过程的静态稳定性与对象尺寸相关，所以实验中只有上升阶段而无下降段，而数值模拟中有下降段。

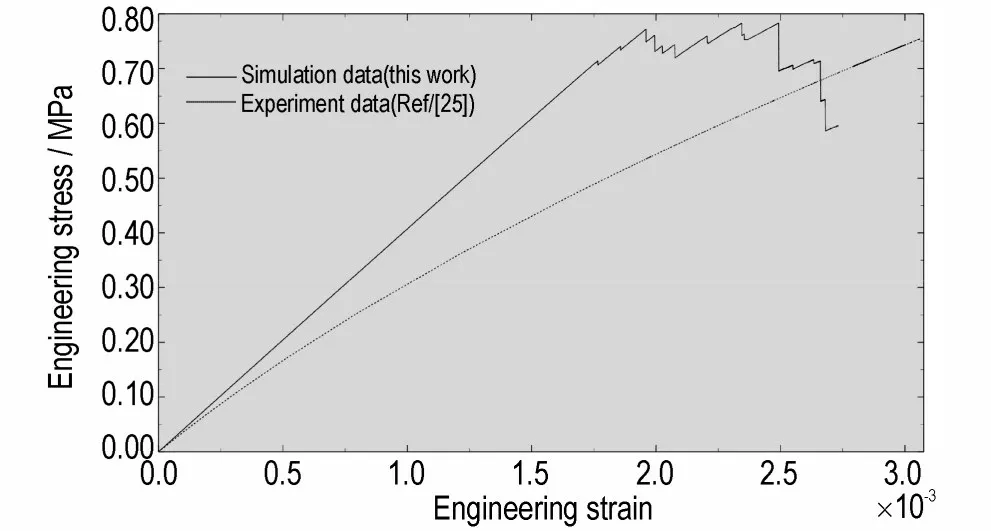
图11 拉应力应变关系的数值模拟与实验数据［25］结果对比Fig.11 Comparison of the stress-strain relationsip of simulation with the experimental data［25］

图12 为模拟中PBX-9501 主要裂纹的形成过程，其 中a、b、c 分 别 为y方 向 应 变 为0.0015、0.0025、0.0027 时的微裂纹的形成及分布。由于PBX-9501 颗粒的刚度远远大于黏结剂刚度，在数值模拟中接近刚性体的变形行为。从图12 可以看出，界面刚度退化以及微裂纹的产生是由于PBX-9501 整体变形的协调性与严重的局部刚度不均匀之间的矛盾所引起的。过大的局部刚度需要释放，整体上主裂纹方向垂直于应变加载方向，并沿大颗粒边界扩展；局部裂纹的产生与颗粒间相对位移相关。图13 为图12c 中a、b、c 3 个区域放大图，模拟中微裂纹产生的结果由图13 可见，其中a为相邻颗粒的相对错开而产生的微裂纹，b 为相领颗粒相对张开而产的微裂纹，c 为相邻颗粒的相对转动而产生的微裂纹。

图12 拉伸载荷下模型的断裂过程Fig.12 Fracture process under tension

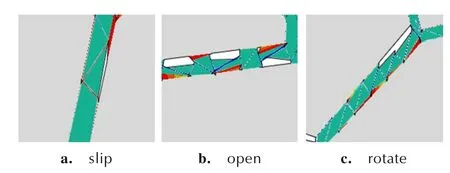
图13 协调变形中微裂纹产生的3 种情况Fig.13 Three cases of microcracks in coordinated deformation

在图11 中数值模拟与实验结果存在的差异有以下原因。一是数值模拟的模型过于理想化，实际上PBX 内部包含着大量不规则、跨尺度的孔隙［26-28］，以及PBX 在制备与存储过程中在各种复杂载荷作用下使得部分界面产生刚度退化甚至产生微裂纹，会使得数值模拟的初始刚度偏高。 二是巴西圆盘实验中PBX-9501 的应变与应力关系是在一定的假设下通过间接测量而得出，表现为当应力达到断裂强度时PBX-9501 就产生宏观裂纹。三是数值模拟结果与代表体积元的尺寸密切相关，存在尺寸效应。从应变和能量两个角度分析收敛性，如图14 所示。

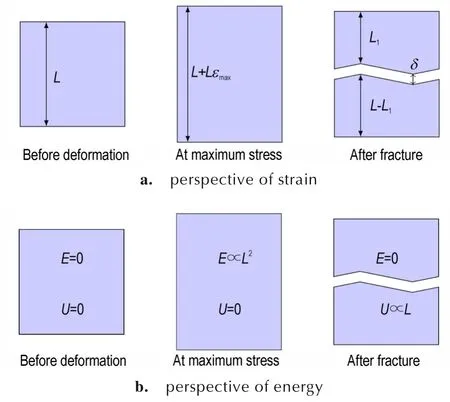
图14 从两种角度分析收敛性Fig.14 Analysis of convergence from two perspectives

从应变的角度来看，如图14a，其中εmax为最大应力时对应的应变，δ为界面断裂时的张开位移，在达到最大拉伸强度前，应变几乎均匀产生于代表体积元，而达到最大拉伸强度之后应变的产生主要来源于断裂面之间的位移，代表体积元的尺寸越小则数值模拟的应变与应力关系中的刚度退化阶段就越大。而当代表体积元的尺寸L足够大，则无刚度退化阶段。用数学公式可表达为

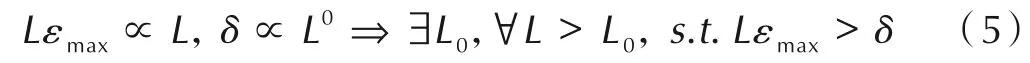
界面断裂所需位移完全能够由代表体积元应变减小而产生的位移提供，则数值模拟的应变与应力关系中刚度退化阶段将不存在，达到最大应力时主裂纹产生过程不可能静态平衡，是一个失稳的过程，采用静力隐式分析难以收敛。

从能量的角度分析，如图14b，其中E为弹性能，U为断裂能，代表体积元在最大应力时的弹性能正比于代表体积元尺寸的平方L2，而断裂面所需能量正比于代表体积元的尺寸L。随着L的增大，当弹性能大于断裂能时裂纹的扩展不需要外界能量，主裂纹产生是一个失稳的过程。用数学公式可表达为

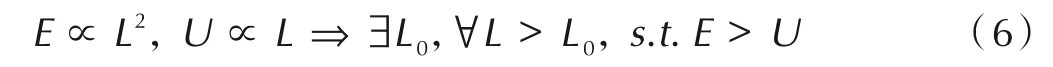
尽管实际断裂过程中所需的断裂能与断裂面相对位移并非简单的线性关系，但同样可以得出随着代表体积元尺寸的增加进行有限元静力隐式分析时收敛性越差的结论。

5 结论

考虑由到Voronoi 方法得到的模型的局限性，本研究首先通过随机生成三级配圆，并采用大级配最大化方法，在Voronoi 方法的基础上进行改进，建立了更加符合实际的不同级配下晶粒分布的二维几何模型。改进后的模型中组分含量可通过黏结剂厚度调节，颗粒分布随机，相对于单纯的Voronoi方法得到的模型更加符合实际PBX 的细观结构。由改进后的模型建立二维代表体积元，采用三阶段黏结界面损伤本构关系，对含有细观结构的PBX-9501 进行静态拉伸下的界面脱粘进行了数值模拟，研究了静态拉伸下颗粒与黏结剂界面力学行为。结果表明，本研究建立的模型所模拟的应力-应变曲线与实验数据对比存在较小的差异。本研究从PBX-9501 细观结构、实验与数值模拟3 个方面分析了产生差异的来源，得出进行有限元隐式静力分析界面脱粘行为时代表体积元的尺寸越大则收敛性越差的结论。