基于国密SM2 和SM9 的加法同态加密方案*

唐 飞, 凌国玮, 单进勇

1. 重庆邮电大学计算机科学与技术学院, 重庆 400065

2. 重庆邮电大学网络空间安全与信息法学院, 重庆 400065

3. 北京数牍科技有限公司, 北京 100083

1 引言

近年来, 人们更加倾向于使用公有云或互联网存储数据, 进而降低存储成本. 为了实现用户数据的隐私保护机制, 常用的方法是将数据加密后再存入数据库中. 然而, 当用户要对加密的数据进行相关计算, 例如求和、内积等, 如果是普通的加密方法, 则用户需要自己下载数据再解密并计算, 或授权云服务提供商获取原始数据从而实现云计算服务. 针对这一问题, Rivest 等人[1]提出了同态加密的概念, 同态加密是一种可对密文进行同态运算的加密方案, 即对密文计算后再解密可以得到对原始数据直接计算的结果, 从而同时实现云存储数据的机密性与用户的隐私保护性.

同态加密方案一般分为全同态加密和部分同态加密两类[2]. 其中, 全同态加密方案[3]可对密文进行任意的同态计算, 部分同态加密方案只能单独对密文做加法或乘法同态计算. 尽管部分同态加密方案只能支持单一的同态计算, 但这类方案的实现效率往往比全同态加密方案高很多, 因此具有更高的可用性. 部分同态加密方案中以加法同态加密方案最为典型, 已广泛应用于数据聚合[4]、多方计算[5]、联邦学习[6]、区块链支付系统[7]等现实应用场景中. 例如, 无线传感器网络中的数据聚合方案[4]利用加法同态加密保护了数据隐私, 同时降低了网络带宽; 智能电网[5]利用加法同态加密对用户电量数据进行加密, 从而实现电量的隐私保护与快速求和计算; 联邦学习[6]利用加法同态加密使得在多方联合训练模型的同时保持原始数据不泄露给服务方.

加法同态加密方案中若干密文运算后的结果为对应明文之和的密文, 即Enc(m1)∗Enc(m2) =Enc(m1+m2). 现有的经典加法同态加密方案均为国外研究人员设计, 例如Paillier[8]、基于ElGamal[9]的同态加密方案Exponential ElGamal[10](简写为Exp-ElGamal)、BGN[11]等, 缺乏支持国密标准的加法同态加密方案. 因此, 在需要同态加密的应用场景中一般都使用上述方案, 尤其是Paillier 方案使用特别广泛, 例如微众银行的FATE 联邦学习平台[12]等均使用Paillier 方案作为其基础核心组件. 截至目前, Paillier 论文[8]已被引用7762 次(Google 学术被引数据).

商用密码是我国自主研发的密码标准方案, 常用的商密标准包括 SM2[13]、SM3[14]、SM4[15]、SM9[16]等. 其中, SM2 是普通的公钥密码方案, SM9 是基于身份的公钥密码(标识密码) 方案. SM2和SM9 均基于椭圆曲线, 在同等安全强度下相对RSA[17]、Paillier[8]等类型的公钥密码方案而言, 具有密钥更短、系统参数更小等优点, 并且硬件实现椭圆曲线密码算法所需逻辑电路门数要较RSA 类型少得多, 功耗也更低. 目前, 国密系列标准方案已得到广泛应用, 研究者们也基于国密方案构造了多种类型的密码方案, 例如区块链隐私保护[18]、多接收方公钥加密[19]、多方签名[20,21]、环签名[22,23]、门限解密[24]、广播加密[25]、标识签密[26]、范围证明[27]等.

如上所述, 目前缺乏基于国密标准的同态加密方案, 使得相关企业只能采用Paillier 等加法同态加密方案. 针对这一问题, 本文基于国密SM2 和SM9 设计具有加法同态性质的公钥加密方案, 本文的主要贡献如下:

分别基于国密SM2 和SM9 构造了加法同态加密方案和标识加法同态加密方案. 两个方案均兼容原标准方案中的推荐曲线参数和密钥生成算法, 仅对原方案的加解密算法作出调整, 使新方案在尽可能保留原方案结构的基础上具备加法同态性质. 对所提方案做安全性与效率分析. 安全性方面, 首先通过与原标准方案的密文形式进行对比, 所提方案与原标准方案具有类似的安全性, 再证明了所提方案具有INDCPA 安全性. 效率分析方面,编程实现所提方案,并与Paillier[8]、Exp-ElGamal[10]、Twisted-ElGamal[7]方案做对比分析, 实验结果表明所提方案的绝大多数指标均优于Paillier、Exp-ElGamal. 其中所提SM2加法同态加密方案的解密耗时大约仅为Exp-ElGamal 方案的3/5, Paillier 方案的1/8; SM9 加法同态加密方案的解密耗时大约仅为Exp-ElGamal 方案的3/4, Paillier 方案的1/6.

为了降低私钥泄露导致密码系统可用性和安全性受损的风险, 进一步构造具有门限解密性质的加法同态方案. 门限解密方案的安全性与一般的基于Shamir 秘密共享[28]的门限解密方案类似, 为基于国密SM2 和SM9 的同态加密方案的分布式应用提供理论支撑.

2 预备知识与定义

2.1 椭圆曲线与相关复杂性假设

令p是大素数,E为定义在有限域Fp上的椭圆曲线,G为椭圆曲线的q阶基点(xG,yG), 群G 代表以G为生成元生成的椭圆曲线点集. 若x ∈Z∗q, [x]G代表椭圆曲线基点G的x倍点. 椭圆曲线上的运算规则此处不再赘述.

在SM2 方案[13]中, 推荐的曲线方程为y=x3+ax+b, 建议的参数a,b分别如下:

a: 787968B4 FA32C3FD 2417842E 73BBFEFF 2F3C848B 6831D7E0 EC65228B 3937E498;

b: 8542D69E 4C044F18 E8B92435 BF6FF7DE 45728391 5C45517D 722EDB8B 08F1DFC3.

假设1离散对数(discrete logarithm) 问题. 给定(E,G,p,q) 与群G, 随机选择P ∈G, 计算一个随机数, 满足P=[x]G是困难的.

假设2CDH(computational Diffie-Hellman)问题. 给定(E,G,p,q)与群G, 随机选择[x]G,[y]G ∈G, 计算[xy]G是困难的.

假设3DDH(decisional Diffie-Hellman)问题. 给定(E,G,p,q)与群G,随机选择[x]G,[y]G,[z]G ∈G, 判断z=xy是否成立是困难的.

2.2 双线性映射与相关复杂性假设

令G1,G2为阶为大素数N的加法循环群, GT为阶为大素数N的乘法循环群,P1,P2是G1,G2的生成元, 若x ∈Z∗N, [x]Pi代表生成元P1,P2的x倍, 其中i ∈{0,1}, 满足:

(1)双线性: 对任意的a,b ∈ZN,e([a]P1,[b]P2)=e([b]P1,[a]P2)=e(P1,P2)ab;

(2)非退化性:e(P1,P2)̸=1;

(3)可计算性: 存在有效算法能高效计算双线性对e, 如基于Weil 对[29]的改进算法.

在SM9 方案[16]中, 群G1,G2中元素均为椭圆曲线上的点, 曲线方程采用y2=x3+5.

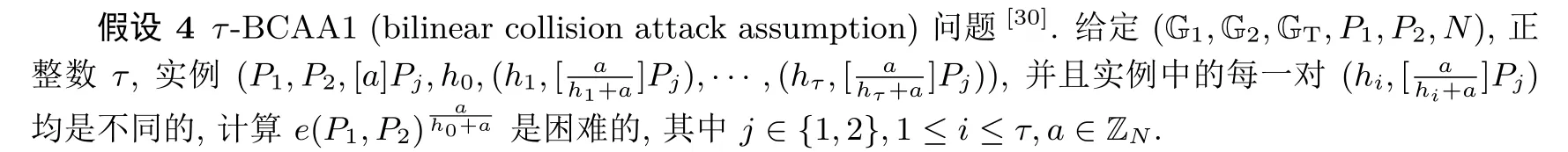
2.3 加法同态公钥加密

一个普通的加法同态加密方案包含如下四个算法.

(1)系统建立Setup(1ℓ): 系统建立算法输入安全参数ℓ, 输出公共参数pp, 包含明文空间M、密文空间C 等系统公开参数的描述.

(2)密钥生成KeyGen(pp): 密钥生成算法输入系统参数pp, 输出用户公钥pk 和私钥sk.

(3)加密Enc(pk,m): 加密算法输入公钥pk 与明文m ∈M, 输出密文c ∈C.

(4)解密Dec(sk,c): 解密算法输入私钥sk 与密文c ∈C, 输出m ∈M; 否则输出⊥, 代表解密失败.方案具有如下三个性质.

(1)正确性. 对于所有pp←Setup(1ℓ), (pk,sk)←KeyGen(pp),c ←Enc(pk,m), 均有m ←Dec(sk,c).

(2)同态性. 所有pp←Setup(1ℓ), (pk,sk)←KeyGen(pp), 对于任意两个密文c1←Enc(pk,m1),c2←Enc(pk,m2), 均有c1∗c2=Enc(pk,m1+m2).

(3)安全性. 加法同态公钥加密方案的安全性要求敌手无法从密文得到关于明文的任何信息.

2.4 加法同态标识加密

标识密码即基于身份的密码(identity-based cryptography, IBC), 是Shamir[31]于1984 年提出的概念, 在标识密码方案中, 用户的私钥由密钥生成中心(key generation center, KGC) 根据主密钥和用户标识计算得出, 用户的公钥由用户标识充当, 从而用户不需要通过第三方保证其公钥的真实性. 与基于公钥基础设施(public key infrastructure, PKI) 的密码方案相比, 标识密码方案中的密钥管理环节可以适当得到简化. 在大数据隐私计算中, 一般的加法同态加密方案由于更新密钥需要花费太多的时间, 故越来越多人开始注意到基于身份的同态加密方案, 例如Gentry 等人[32]基于容错困难(learning with errors,LWE) 问题构造的同态加密方案等.

一个加法同态标识加密方案通常由如下四个算法组成.

系统建立Setup(1ℓ): 算法输入一个安全参数ℓ, 输出加密主公钥mpk 和加密主私钥msk, 以及系统参数pp, 其中包含明文空间M、密文空间C、加密主公钥mpk 等公开参数的描述.

密钥生成KeyGen(pp,msk,id): 密钥生成算法输入加密主私钥msk 与用户标识id, 输出用户私钥skid.

加密Enc(id,m): 加密算法输入用户标识id 与明文m ∈M, 输出密文c ∈C.

解密Dec(sk,c): 解密算法输入用户私钥skid与密文c ∈C, 输出m ∈M; 否则输出⊥, 代表解密失败.

方案具有如下三个性质.

正确性. 对于所有(mpk,msk,pp)←Setup(1ℓ), skid←KeyGen(pp,msk,id),c ←Enc(id,m), 均有m ←Dec(skid,c).

同态性. 方案满足对于所有(mpk,msk,pp)←Setup(1ℓ), skid←KeyGen(pp,msk,id), 对于任意两个密文c1←Enc(id,m1),c2←Enc(id,m2), 均有c1∗c2=Enc(id,m1+m2).

安全性. 加法同态标识加密方案的安全性要求敌手无法从密文得到关于明文的任何信息.

2.5 大步小步走(Baby Step Giant Step, BSGS) 算法

2.6 秘密共享

Shamir 秘密共享[28]是构造门限密码方案的基础组件. 在Shamir 秘密共享方案中, 假设一共有n个参与者, 只有当大于等于t位参与者共同参与计算时, 才能恢复秘密值s, 小于t位参与者无法获得关于秘密的任何信息. 令GF(p) 是阶为大素数p的有限域, 秘密信息s ∈Z∗p.

2.6.1 Shamir 秘密共享方案

可信中心给n位参与者{U1,U2,··· ,Un}分发秘密份额, 使得其中任意t位及其以上诚实的参与者才可以重构出秘密信息s, 而任意小于t位的参与者不能得到关于秘密s的任何信息.

2.6.2 Shamir 联合随机秘密共享方案

在无可信中心的情况下, 需要参与者{U1,U2,··· ,Un}联合决定并生成随机的共享秘密值.

3 基于SM2 算法的同态加密方案

SM2[13]是中国于2010 年12 月发布的基于椭圆曲线的公钥密码方案, 并于2012 年3 月成为商用密码标准. 本节基于SM2 构造具有加法同态性质的公钥加密方案.

3.1 方案构造

系统建立. 令A、B分别为加密用户与解密用户, 他们提前设定相同的公共参数pp, 其中p是大素数,E为定义在有限域Fp上的椭圆曲线,G是椭圆曲线的q阶基点, 明文空间M 的比特长度mlen 设为32 比特[7]. 若k ∈, [k]G代表椭圆曲线基点G的k倍点. 密码杂凑函数H:{0,1} →Zq.x||y代表字节串或比特串x与y的拼接.⊕代表比特串之间的异或运算.

密钥生成.B用户随机选取私钥sk∈, 公开公钥pk=[sk]G.

加密. 设用户A需要发送给用户B的消息为m, 用户A需要进行以下计算:

标准SM2 方案[13]的c2部分是m ⊕t, 其中t= KDF(x2||y2,mlen), KDF :{0,1}∗×mlen→{0,1}mlen. 但由于本方案的后续计算过程没有用到t, 故在本方案中无需计算该值.

解密. 用户B收到用户A发送的密文c=(c1,c2,c3), 进行如下运算解密:

(1) 验证c1是否满足椭圆曲线方程, 若不满足则报错并退出;

(2) 计算椭圆曲线点S=[h]c1, 其中h=1, 若S是无穷远点, 则报错并退出;

(3) 计算椭圆曲线点[sk]c1=(x2,y2),[m]G=c2−[sk]c1;

(4) 利用BSGS 算法从[m]G中恢复m;

(5) 若是同态运算后的密文, 直接输出明文m, 解密完成并退出;

(6) 否则计算u=H(x2||m||y2), 判断u=c3是否成立. 若成立, 输出明文m, 否则报错并退出.

标准SM2 方案[13]支持消息完整性校验, 故本文提出的基于SM2 的同态加密方案相比一般的加法同态加密方案还具有密文校验的功能. 然而c3部分是密码杂凑函数生成的摘要, 不具备加同态性, 所以无法支持同态计算后的密文校验. 但从实际应用来看, 这是可以接受的. 如联邦学习中最典型的两方纵向(无第三方存在的情况), 双方通过加密自身训练过程中的中间值, 进而共同完成模型训练. 然而, 进行密文计算(同态加、标量乘等操作) 的一方无法对密文进行解密, 同时解密一方解密得到的明文一般为不可区分的随机值, 失去了密文校验的价值, 如两方纵向逻辑回归[34]; 另一方面, Paillier[8]、Exp-ElGamal[10]、BGN[11]等使用广泛的同态方案均不支持同态密文校验, 但仍被广泛使用, 这也能说明同态密文校验并不是必须的. BSGS 算法无法在有效的时间内恢复比特长度过长的明文, 故限定了明文空间M 的比特长度,此处以32 比特[7]为例.

正确性. 如果用户A、B是诚实的, 那么有:

3.2 门限解密

门限密码概念由Desmedt[35]提出, 假设系统中存在t位参与者{U1,U2,··· ,Un}, 他们共享解密私钥sk, 当对密文进行解密时, 至少需要t位参与者共同参与才能恢复密文所对应的明文, 少于t位的参与者无法得到关于明文的任何信息. 门限解密能够降低或避免因个体完全掌握解密密钥而导致的滥用权限、密钥丢失, 或某个参与者被攻击者完全控制而造成系统瘫痪等安全风险, 使系统的容错率和安全性得到较大提高. 一般的门限密码方案可分为有可信中心和无可信中心两类. 当可信中心存在时, 由可信中心进行秘密分发, 减少参与者之间的通信量和计算量; 但一个被所有参与者都信任的可信中心可能并不存在, 此时需要参与者联合实现对秘密的分享, 即无可信中心方案. 本节基于Shamir 秘密共享[28]构造3.1 节加法同态加密方案的门限解密方案.

系统建立. 系统建立阶段的公开参数与符号定义在有可信中心时由可信中心产生, 无可信中心时由t位参与者共同决定, 它们应与3.1 节系统建立的公开参数与符号定义保持一致.

密钥生成. 当存在可信中心时, 由可信中心完成生成密钥对(pk,sk)、公开公钥pk、生成关于sk 的秘密份额、秘密份额的分发. 可信中心需进行如下运算:

3.3 安全性分析

基于SM2 的加法同态加密方案是将标准SM2 方案的密文c2部分从m ⊕t变为[m]G+[k]pk, 从而使方案具备加法同态性. 其中t是由[k]pk 通过密钥派生函数KDF 生成的比特串, 即t近似于的[k]pk摘要. 也就是说标准SM2 方案的c2部分是将明文m与[k]pk 的摘要进行异或得到的. 而本文所提出的基于SM2 的加法同态加密方案是将[m]G与[k]pk 直接相加. 两种方案的密文c2部分生成本质上是一致的, 均为明文与[k]pk 进行运算. 且在其余运算过程与密文部分均不变的的前提下, 基于SM2 的加法同态加密方案与标准SM2 方案应有类似的安全性. 从另一个方面来说, 基于SM2 的加法同态加密方案的c2密文形式与Exp-ElGamal 也是一致的, 也可说明该方案与Exp-ElGamal 也有类似的安全性.

定理1如果DDH 问题是难解的, 那么基于SM2 的加法同态加密方案是IND-CPA 安全的.

证明:如果存在一个概率多项式时间(probabilistic polynomial time, PPT) 敌手A能以不可忽略的优势ε打破基于SM2 的加法同态加密方案, 则可以构造挑战者C以不可忽略的优势解决DDH 问题.

系统建立.C得到DDH 问题的实例([x]G,[y]G,z[G]). 然后运行系统建立算法, 得到系统参数pp,设置公钥pk=[x]G. 将pp 与pk 发送给A.

挑战.A提交两个任意的明文m0,m1∈M 给C.C随机选择一个比特α ∈{0,1}, 进而计算c∗=([y]G,[mα]G+[z]G), 然后将c∗发送给A.

猜测.A输出对α的猜测α′. 如果α=α′, 则说明A获胜. 定义:

定义A获胜的优势为:

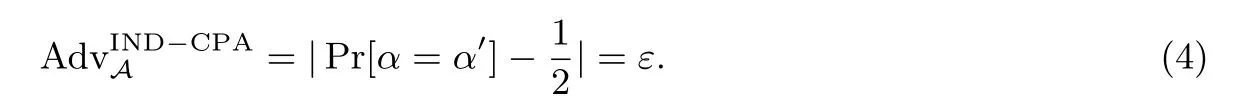
那么C解决DDH 问题的优势为:

本节提出的门限解密方案是基于Shamir 秘密共享构造的, 采用了Desmedt[35]构造的ElGamal 的门限解密方案的思路. 同时关于以基于Shamir 秘密共享方案构造公钥加密方案的门限解密的安全性已在多篇文献中得到证明, 如文献[24,35] 等, 故本文不再赘述.

4 基于SM9 算法的同态加密方案

2016 年国家密码管理局正式发布SM9 标准[16], 它是一种基于双线性对的标识密码方案, 同时也是我国商用密码算法中的第一个标识密码算法. 本节基于SM9 构造具有加法同态性质的标识加密方案.

4.1 方案构造

系统建立. 令A、B分别为加密用户与解密用户. KGC 提前设定公开参数pp, 其中G1、G2为阶为素数N的加法循环群,P1、P2是它们的生成元, GT为阶是素数N的乘法循环群, hid 是加密私钥生成函数识别符.e是从G1×G2到GT的双线性对, 明文空间m的比特长度mlen 设为32 比特[7]. 若u是随机数, [u]P代表群G1、G2中元素P的u倍. 密码杂凑函数H1:{0,1}∗×N →Z∗N, 消息验证码函数MAC :{0,1}∗×GT→Z∗N, 密钥派生函数KDF :{0,1}∗×klen→{0,1}klen, 其中klen = mlen+256.随机选择msk∈Z∗N作为加密主私钥, 计算G1中的元素mpk=[msk]P1作为加密主公钥, 则加密主密钥对为(mpk,msk). KGC 保存msk, 公开mpk.

密钥生成. 设用户B的标识为idb, KGC 在有限域FN上计算t1=H1(idb||hid,N)+msk, 若t1=0则需重新执行系统建立算法, 否则计算t2=msk·t−11. 用户B的解密私钥skidb=[t2]P2.

加密. 设用户A需要发送给用户B的消息为m. 用户A应实现以下运算步骤:

标准SM9 加密方案[16]的c2部分是m ⊕K1, 其中K1是KDF 生成的K的前mlen 比特. 由于本方案中后续无需用到K1, 故K1部分在本方案中被丢弃.

解密. 用户B收到用户A发送的密文c=(c1,c2,c3), 进行如下计算解密:

与SM2 同态加密方案类似, 单个密文可以通过c3进行解密校验. 但是由于c3是消息验证码函数生成的, 不具备加法同态性, 因此无法校验同态计算后的密文. 同时本方案需要利用BSGS 算法从gm中恢复出m, 此处同样限定明文空间M 的比特长度mlen 为32 比特.

正确性. 如果用户A、B是诚实的且KGC 未被攻击, 那么一定有:

4.2 门限解密

Boneh 等人[29]最早将门限思想引入到基于身份的加密方案中, 其目的主要是为了解决KGC 完全掌握系统主私钥msk, 从而导致的权限过大问题. 主要采用的方法是将msk 分割为秘密份额分发给各个分KGC, 每个分KGC 为用户生成部分用户私钥份额, 至少需要t个KGC 产生的用户私钥份额, 才能构成完整的用户私钥, 完成对密文的解密, 因此也被称作分布式密钥生成. 但此方法存在两个弊端: 首先要求KGC 必须实时在线, 其次是必须要足够的t个KGC 才能完成解密. 所以Baek 等人[36]认为, 在基于身份的门限解密方案中, 直接对用户密钥进行分割也是有必要的, 此类门限解密和传统的基于PKI 的门限解密类似, 单个KGC 作为可信中心存在. 于是我们可将基于身份的门限解密方案分成单中心(单个KGC) 与多中心(多个KGC) 两种类型. 本节以假设系统中存在n位参与者{U1,U2,··· ,Un}, 然后再基于Shamir 秘密共享构造4.1 节的门限解密方案.

系统建立. 单中心情况下, 仅有一个KGC 存在. KGC 首先参照4.1 节系统初始化部分得到公开参数pp 与相关符号定义, 然后选择随机数t2= msk·[H1(idb||hid,N)+msk]−1∈Z∗N−1作为秘密, 通过计算H1(idb||hid,N) 与上式联立可求得加密主私钥msk, 进而可以计算G1中的元素mpk = [msk]P1作为加密主公钥. 最后保存msk, 公开mpk.

多中心情况下, 系统中存在n′个可信中心{KGC1,KGC2,··· ,KGCn′},n′≥2t −1, 它们需要共同确定公开参数与相关符号定义. 由于SM9 方案的用户密钥形式为skidb= msk·[H1(idb||hid,N)+msk]−1P2, 为了防止msk 泄露, 此处不能直接以msk 作为秘密. 我们首先将用户密钥形式写为skidb=[1−H1(idb||hid,N)·[H1(idb||hid,N)+msk]−1]P2, 然后以[H1(idb||hid,N)+msk]−1作为秘密实现门限解密. KGC 们为了生成秘密份额, 并公开mpk, 需要进行如下运算:

多中心情况下, 此阶段KGC 们不需要做出任何运算.

加密. 加密算法中, 单中心情况与多中心情况是一致的, 加密用户直接使用标识idb加密发送的消息m得到密文c即可, 具体的计算过程见4.1节加密部分.

4.3 安全性分析

基于SM9 的加法同态加密方案与基于SM2 的加法同态加密方案采用了类似修改思路, 将标准SM9方案的密文c2部分从m ⊕t变为gm·w, 从而使方案具备加同态性.t是由w、密文c1部分、用户标识通过密钥派生函数KDF 生成的比特串. 然而,w是由c1与p2通过双线性对e求得的GT群元素, 用户标识也包含在c1中. 故KDF 的主要参数就是w, 所以t实质上近似于w的摘要. 由此可知, 标准SM9方案的c2是由明文m与w的摘要t进行异或运算得到的, 而本文提出的基于SM9 的加法同态加密方案是将明文m以gm的形式放到乘法群GT中再直接与w相乘得到的. 两种方案的密文c2部分本质是一样的, 均是明文m与w的运算. 故在其他运算过程以及密文部分不变的前提下, 两种方案应有类似的安全性.

定理2令密码杂凑函数H1是随机谕言机, 如果DDH 问题是难解的, 那么基于SM9 的加法同态加密方案是IND-CPA 安全的.

本节所提的门限解密方案是以Shamir 秘密共享为基础构造的, 构造思想与Baek 等人[36]构造的基于身份的门限解密方案一致. 此类门限解密方案的安全性已在文献[36] 中得到证明, 本文不再赘述.

5 效率分析

本文的主要工作是分别基于国密SM2 和SM9 构造了加法同态加密方案. 为保证本文所提出同态加密方案的高效性, 本节将对128 比特安全等级(256 位椭圆曲线、3072 位Paillier)、明文比特长度为32比特下(参照Chen 等人[7]的方案) 的SM2 同态加密方案、标准SM2 加密方案、SM9 同态加密方案、标准SM9 加密方案、Exp-ElGamal 方案、Twisted-ElGamal 方案、Paillier 方案进行对比实验. 选取Exp-ElGamal 方案、Paillier 方案进行对比实验的原因是因为它们是最常用的加法同态加密方案, 而选取Twisted-ElGamal 方案是因为它的密钥与密文长度是相对较小的, 并且能很好的应用于Sigma 协议与范围证明协议. 测试的硬件平台采用Intel i7-1165G7 处理器、内存为16 GB、主频为2.8 GHz. 操作系统为Ubuntu 18.04, 编程语言是Go 1.19. 标准SM2 和SM9 加密方案使用的代码库为cryptogm[38], 本文所提出的同态加密方案的具体实现[39]也是基于cryptogm 代码库; Exp-ElGamal 方案使用的将Go 语言版Bitcoin 的btcec[40]里的EC-ElGamal 方案改为Exp-ElGamal 方案[41]; Paillier 方案使用代码库Go-Paillier[42]; Twisted-ElGamal 方案使用Chen 在GitHub 上提供的开源代码库[43].

5.1 通信与存储开销

从解密算法中可以看出, 如果需要得到明文m, 那么必须求解一个离散对数. 加快求解离散对数的算法例如kangaroo 算法[44]、Galbraith-Ruprai 算法[45]、BSGS 算法[33]、Bernstein-Lange 算法[46]等.Chen 等人[7]对它们进行了算法复杂度的分析, 且比较了它们的特性. 例如, kangaroo 算法与Galbraith-Ruprai 算法的平均时间复杂度为O(2mlen/2) 且需要一个固定的内存开销; BSGS 算法平均时间/空间复杂度均为O(2mlen/2), 且它可通过调整参数的方式灵活调整时间以及空间开销. Bernstein-Lange 算法的平均时间/空间复杂度为O(2mlen/3), 但它并不支持并行计算. 本文选择BSGS 算法恢复明文, 因为它的时间与空间开销是灵活的, 并且支持并行计算. 经过实验分析, 该算法需要128 MB 左右的内存空间.

经过对比分析, 各方案的密钥、密文长度如表1 所示.

表1 各种方案的密钥与密文长度(明文长度为32 比特, 单位bits)Table 1 Key and ciphertext length for various schemes (plaintext length is 32 bits, unit: bits)

需要注意的是, 表1 中密文长度是在已知明文比特长度为32 比特下进行计算得到的. 并且标识密码方案(标准SM9 方案、基于SM9 的同态加密方案) 的用户公钥为用户标识, 即公钥长度就是标识长度, 故在表中没有给出它们的公钥长度.

5.2 计算开销

经过实验测试, 各加密方案的效率计算开销结果如表2 所示.

标准SM2 方案与标准SM9 方案不具备同态性, 故表2 中没有同态加与标量乘的实验结果.

关于基于SM2 的同态加密方案, 如表2 所示, 本文所提出的基于SM2 的同态加密方案相较于经典加法同态加密方案的Exp-ElGamal、Paillier 在各个指标上均存在效率优势. 解密运算方面, 本方案的解密耗时大约仅为Exp-ElGamal 方案的57%, Paillier 方案的12%. 与标准SM2 方案相比, 加密效率有所降低的原因是由于密文部分的生成从密钥扩展和异或运算(即t= KDF(x2||y2,mlen) 与m ⊕t) 变成了椭圆曲线点乘与点加运算(即[m]G与[m]G+[k]pk), 后者的效率是低于前者的; 解密效率降低的原因是需要进行BSGS 算法恢复明文m.

表2 各种方案的效率测试(运行1000 次的平均值, 单位: ms)Table 2 Efficiency tests of various schemes (average value of 1000 runs, unit: ms)

关于基于SM9 的同态加密方案, 如表2 所示, 本文所提出的基于SM9 的同态加密方案在各个指标上与Paillier 方案相比均有一定优势, 与Exp-ElGamal 方案相比也仅在加密运算上不及. 解密运算方面, 本方案的解密耗时大约仅为Exp-ElGamal 方案的75%, Paillier 方案的16%. 所以该方案相较于其他加法同态加密方案仍是高效的. 同时, 该方案的密文c2是一个GT群元素而非一个椭圆曲线的点, 无需做椭圆曲线点加法时需要的模逆运算, 而模逆运算是相当耗时的, 所以该方案的同态加运算效率很高. 与标准SM9 方案相比, 加密效率有所降低的原因是由于密文c2部分的生成从异或运算(m ⊕K2) 变成了群上的模幂与乘法运算(gm与gm×w), 后者的耗时高于前者. 解密效率降低的原因同样是需要进行BSGS 算法恢复明文m.

综上所述, 本文提出的基于国密SM2 和SM9 的同态加密方案与常用的加法同态加密方案(Exp-ElGamal、Paillier) 相比在各个运算指标上均是高效的. 解密运算方面, 所提SM2 加法同态加密方案的解密耗时大约为Exp-ElGamal 方案的3/5, Paillier 方案的1/8; SM9 加法同态加密方案的解密耗时大约为Exp-ElGamal 方案的3/4, Paillier 方案的1/6. 尽管基于SM9 的同态加密方案的加密效率不及Exp-ElGamal, 但它的同态加运算效率很高, 在大规模联邦学习和隐私计算中仍应具有较大优势. 为了便于读者参考, 我们将本文所提两个加密同态加密方案的源代码的上传至Github 网站中(详见https://github.com/ShallMate/-Homomorphic-SM2-9).

6 结束语

本文基于国密SM2 与SM9 设计了具有加法同态性质的公钥加密方案, 并构造了相应的门限解密方法, 解决了目前缺乏基于国密标准的同态加密方案这一问题, 使国密算法能够用于同态加密场景. 对本文所提方案进行了安全性证明, 然后编程实现了本文所提同态加密方案, 实验结果表明本文提出的两个加法同态加密方案在大多数指标上与经典的Exp-ElGamal、Paillier 方案相比均占优势, 其中SM2 加法同态加密方案的解密耗时大约仅为Exp-ElGamal 方案的3/5, Paillier 方案的1/8; SM9 加法同态加密方案的解密耗时大约仅为Exp-ElGamal 方案的3/4, Paillier 方案的1/6.