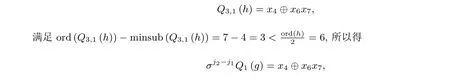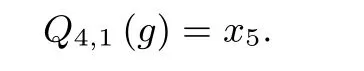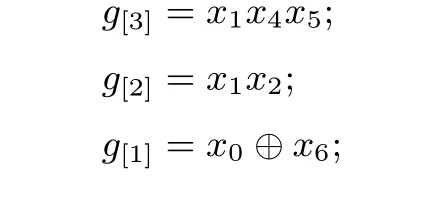h = g ∗g 型布尔函数的星积分解*
2022-07-13孙泽昊王中孝赵肖鑫郑群雄
孙泽昊, 王中孝, 赵肖鑫, 郑群雄
战略支援部队信息工程大学, 郑州 450001
1 引言
序列密码作为对称密码的重要分支之一, 不仅在军事上扮演着重要角色, 它还在外交、政府以及商业领域起着至关重要的作用, 比如GSM 中的A5/1[1]、WEP 中的RC4[2]、蓝牙中的E0[3]、3GPP 中的Snow 3G[4]和ZUC[5]以及面向5G 应用场景设计的Snow V[6]和Snow VI[7]等都是序列密码算法.
随着密码分析技术的发展, 序列密码的设计已经进入非线性驱动的时代. 非线性反馈移位寄存器(nonlinear feedback shift registers, NFSRs) 是一类重要的非线性序列生成器, 在序列密码中广泛使用,例如欧洲序列密码计划eSTREAM 项目最终胜选的两个算法Grain[8]和Trivium[9]都使用NFSR 作为重要部件, 其中Trivium 在2012 年成为国际标准密码算法.
串联结构是NFSRs 的一种重要结构模型, 它是1970 年由美国学者Green 等人[10]首次提出的. 通过引入布尔函数的星积运算(也称∗运算), Green 等人证明了以f1(x0,x1,··· ,xn) 为特征函数的NFSR串联到以f2(x0,x1,··· ,xn) 为特征函数的NFSR 和以f1∗f2为特征函数的NFSR 生成相同的序列簇.对设计者而言, 串联结构可以有效地控制NFSR 的电路深度和输出序列的周期. 例如, Grain v1 算法采用80 级本原线性反馈移位寄存器(linear feedback shift register, LFSR) 来控制80 级NFSR, 使得输出序列的周期都是280−1 的倍数. 对攻击者而言, 更关心的是NFSR 的串联分解问题, 即能否将一个较大级数的NFSR 分解为两个级数较小的NFSR 的串联, 通过结构的等价变形来有效降低攻击的复杂度. 例如当存在分解h=f ∗g, 且f不含常数项1 时, 在某些状态下以h为特征函数的NFSR 就退化为以g为特征函数的NFSR, 特别地, 当g是线性布尔函数时, 这种退化可能会导致非常有效的攻击方法, 从而大大削弱相应算法的安全性.
然而, 如何将一个NFSR 分解为两个级数更小的NFSR 的串联是一个富有挑战性的问题. 到目前为止仅对某些特殊情形有高效的分解算法, 而对一般情形的分解算法仍有待进一步研究. NFSR 的串联分解首先在文献[11] 中研究, 它给出了一种特例, 即右线性星积分解, 可以将特征函数h分解为f ∗l, 其中l是线性布尔函数. 但是由于这种分解算法只利用了最高次项中部分项的信息, 故它得到的候选集并不精确.文献[12] 中给出了右线性星积分解的等价条件, 同时给出了一种改进算法, 因为改进算法利用了所有最高次项的信息, 所以得到了更精确的候选集. 文献[13] 在总结梳理上述两种方法的基础上, 给出了更加具有一般性的高阶差分的方法, 可用于进一步缩小候选集的范围. 文献[13] 也给出了左线性星积分解的高效算法, 得到了很好的结果, 能够直接求解最大阶左线性星积因子. 更重要的是, 文献[13] 还给出了NFSR 的非线性串联分解算法, 但算法实现较为复杂, 对计算和存储都有很高的要求, 对小规模的NFSR 可以有效分解, 但当级数较大时分解算法仍有待进一步优化和改进.
此外, 关于NFSR 串联分解的唯一性, 也有学者进行了研究. 文献[13] 证明了最大阶的左线性星积因子是唯一的; 文献[14] 证明了最大阶的右线性星积因子也是唯一的, 并且举例说明, 在一般情形下, NFSR的串联分解未必唯一; 文献[15] 在研究NFSR 串联分解唯一性的基础上, 给出了当一个NFSR 既存在右线性星积因子分解,又存在左线性星积因子分解时,两种分解方式的内在联系; 文献[16]研究了Grain-like结构串联分解的唯一性, 并证明了Grain v1、Grain-128、Grain-128a 三个算法中驱动寄存器的串联分解是唯一的.
从目前已有结果来看, 对于给定的特征函数h=f ∗g, 其中f和g是两个非线性特征函数, 想要由h分解出f和g并非易事. 考虑到对于随机给定的两个大素数p和q, 如果p,q较为接近, 也即|p −q| 较小, 则可以利用费马因子分解方法[17]由N=pq有效地分解出p和q. 特别是当p=q时, 还可用快速整数开方算法[18]求出p. 那么对于特征函数, 是否也有类似情形呢? 即当f和g较为“接近” 时, 甚至当f=g时, 是否存在由h=f ∗g分解出f和g的高效算法呢? 本文我们研究上述特殊情形的星积分解问题, 以期能为一般的星积分解问题提供借鉴和探索分解之法. 首先, 本文给出h=g ∗g的两个必要条件. 随后, 基于对布尔函数“求偏导” (定义见第2.1 节) 的思想给出两种情形下由h=g ∗g求解g的高效算法, 并给出算法的时间复杂度分析. 与文献[13] 中算法相比, 本文的算法在时间复杂度方面有明显优势.最后, 本文从星积分解的角度给出了两个特征函数较为“接近” 的一种刻画, 并将两个较为“接近” 的特征函数的星积分解问题转化为h=g ∗g的星积分解问题. 此外, 上述结论也可以拓展至h=g ∗g ∗···∗g的星积分解.
本文后续章节安排如下: 第2 节给出本文所需的预备知识; 第3 节给出本文的主要结果, 即关于h=g ∗g的星积分解理论以及星积分解算法; 第4 节首先给出h=g ∗g的另一种求偏导方式的结果, 接着将一类非线性星积分解问题转化为h=g ∗g的星积分解问题, 最后进一步研究了h=g ∗g ∗···∗g的星积分解问题; 第5 节对本文进行总结, 并提出有待进一步研究的问题.
2 准备知识
记“⊕” 为异或加; “+” 为一般的整数加法; “·” 为一般的多项式乘法. 设k ∈R, 记「k⏋为大于等于k的最小整数,⎿k」为小于等于k的最大整数.
2.1 布尔函数
设n是正整数, 一个n元布尔函数为二元域F2上的n维向量空间Fn2到F2上的一个映射. 记全体n元布尔函数构成的集合为Bn. 对f ∈Bn, 其可以唯一地表示为如下形式:

并记T(f) 中所有变元的最大下标与最小下标分别为ord(f) 与minsub(f), 其中ord(f) 通常称为f的阶.
设f(x0,x1,··· ,xn−1)∈Bn, 则f关于变元xi可唯一地表示为如下形式

令h=f ∗g, 则h ∈Bn+m+1. 值得注意的是, 星积运算通常不可交换, 即f ∗g ̸=g ∗f. 称f为h的左星积因子,g为h的右星积因子. 根据上述定义, 易知命题1成立.
命题1设f,g,h为三个布尔函数, 则

其中ϕ为全体线性布尔函数到单变元多项式环F2[x] 的一一映射. 进一步, 记ϕ−1为ϕ的逆, 可知

设f,g是线性布尔函数, 容易验证

2.2 非线性反馈移位寄存器
一个n级Fibonacci 型非线性反馈移位寄存器(简称NFSR) 如图1 所示.
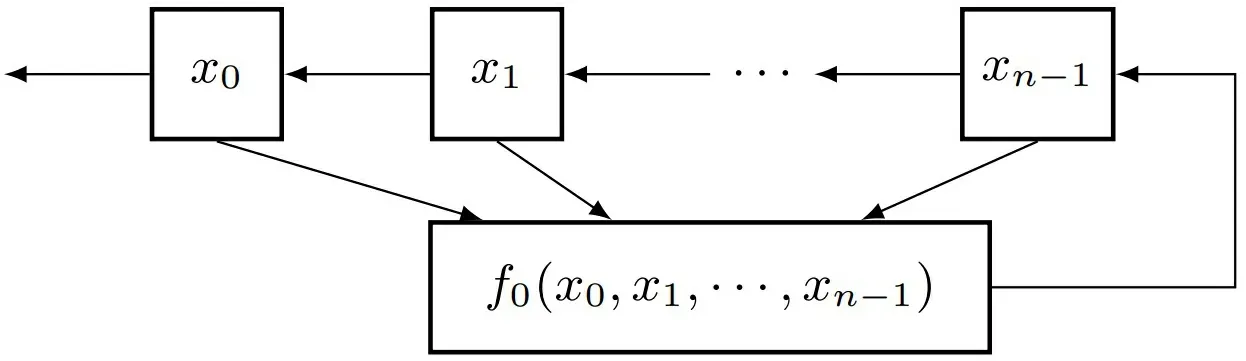
图1 n 级Fibonacci 型非线性反馈移位寄存器Figure 1 n-stage Fibonacci NFSR
其中f0∈Bn称为其反馈函数. 特别地, 若f0是线性的, 则称该NFSR 为线性反馈移位寄存器(简称LFSR). 给定NFSR 的一个初态(a0,a1,··· ,an−1)∈, 其输出序列(a0,a1,···)∈满足n阶递归关系式
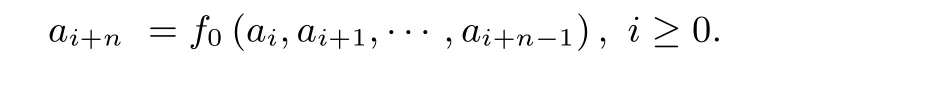
令

称f为该NFSR 的特征函数, 并记该NFSR 为NFSR(f). 遍历2n个初态, NFSR(f) 可以生成2n条不同的序列, 称这些序列构成的集合为NFSR(f) 生成的序列簇, 记作G(f). 进一步, 若G(f) 中的序列均是周期的, 则称NFSR(f) 是非奇异的. 文献[19] 证明了NFSR(f) 是非奇异的当且仅当f可写作如下形式:

称形如式(1)的任一布尔函数为一个n阶非奇异特征函数. 记C为全体非奇异特征函数构成的集合, 记C∗={f ∈C|f(0)=0}.
设f=f0(y0,y1,··· ,yn−1)⊕yn, g=g0(x0,x1,··· ,xm−1)⊕xm分别为两个NFSR 的特征函数.如图2 所示为NFSR(f) 到NFSR(g) 的串联结构, 记作NFSR(f,g). 最左端寄存器为该装置的输出端, 其输出的全体序列构成的集合为G(f,g). 文献[10] 证明了NFSR(f,g) 的输出实际上等价于一个m+n级NFSR(h) 的输出, 即G(f,g) =G(h), 其中后者的特征函数h=f ∗g. 这一结论表明对NFSR 串联结构的研究本质上可以转化为对布尔函数星积性质的研究. 进一步, 文献[12] 证明了NFSR(h) 是非奇异的,当且仅当NFSR(f) 与NFSR(g) 均是非奇异的, 即

图2 NFSR(f) 到NFSR(g) 的串联Figure 2 Cascade connection of NFSR(f) into NFSR(g)
命题2[12]设h=f ∗g, 则h ∈C当且仅当f,g ∈C.
2.3 左线性星积分解
命题3[13]给定h,g ∈C∗, 若存在f1,f2∈C∗使得h=f1∗g=f2∗g, 则f1=f2.
命题3说明, 给定h的右星积因子时,h的左星积因子是唯一的.
设h ∈C∗, 称如下集合

为h的标准项集合(standard term set). 对任意给定的h ∈C∗,h可唯一表示为

其中lt是由h和t唯一确定的线性布尔函数. 称式(2)为h的标准项表示.
例1设h=x0⊕x1⊕x5⊕x1x2⊕x3x4⊕x1x4⊕x1x2x3⊕x2x3x4⊕x1x2x3x4, 则

h的标准项表示为
2)生活习性。桃小食心虫在渭北果区每年发生1~2代,以老熟幼虫在土壤内结茧越冬。一般5月下旬至6月上旬越冬幼虫破茧出土,成虫多产卵于果实梗(萼)洼处。幼虫孵化后,蛀入果实,在果实内蛀食20天左右,老熟后咬破果皮,脱果而出;脱果早的在土表作夏茧化蛹发生第2代,脱果晚的入土越冬。6月下旬至7月上中旬出现第1代成虫,8月上中旬出现第2代幼虫,在采果前大部分脱果。

命题4[13]设h ∈C∗且其标准项表示为

l是线性布尔函数, 则存在布尔函数g使得h=l ∗g当且仅当
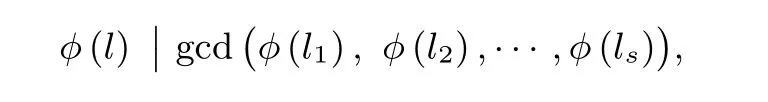
其中gcd 表示F2[x] 中多项式的最大公因式.
注1gcd(ϕ(l1), ϕ(l2),··· ,ϕ(ls))为h的最大阶左线性星积因子.
下面给出求解最大阶左线性星积因子的具体算法.

算法1 GetMaxOrderLeftLinearFactor Input: 特征函数h Output: 最大阶左线性星积分解结果(l,g)1 将h 表示成标准项表示h = l1 ∗t1 ⊕l2 ∗t2 ⊕···⊕ls ∗ts 2 L ←gcd(ϕ(l1), ϕ(l2),··· ,ϕ(ls))3 l ←ϕ−1(L)4 g ←ϕ−1(ϕ(l1)/L)∗t1 ⊕···⊕ϕ−1(ϕ(ls)/L)∗ts 5 Return (l,g)
3 主要结果
本节我们给出在h=g ∗g情形下分解的主要结果. 由于线性情形是简单的, 所以仅考虑deg(g)≥2的情形, 并且我们令g ∈C∗. 注意到g可以唯一地表示为以下形式
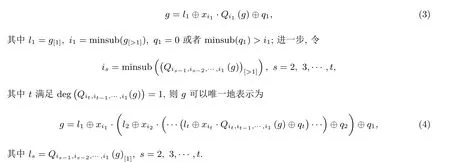
3.1 两个必要条件
由命题2和星积运算的定义知, 如下命题5显然成立.
命题5设h=g ∗g是特征函数, 则ord(h) 为偶数且g是特征函数满足ord(g)=ord(h)/2.
命题5表明, 当ord(h) 为奇数时, 不存在特征函数g, 使得h=g ∗g.
下面进一步讨论h=g ∗g的必要条件. 作为准备, 先给出三个引理.引理1是偏导符号的一个性质,根据第2.1 节符号定义可知引理1是显然成立的;引理2是f ∗g与g的次数关系, 结论证明在文献[20] 中已经给出.

引理2[20]设f是布尔函数且f ̸=0 或1,g是特征函数, 则
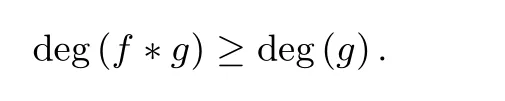
进一步, 上式等号成立当且仅当deg(f)=1.
基于上述两个引理, 可以得到特征函数h的一个基本性质.
引理3若h=g ∗g且h ∈C∗,j1=minsub(h[>1]), 则j1=i1, 并且

证明:由式(3)可知

其中0
命题6若h=g ∗g, 且deg(h)≥2, 则z1≡z2≡···≡zk ≡0 mod 2,且g具有如下形式
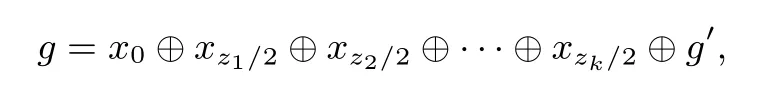
其中deg(g′)≥2 且minsub(g′)>zk/2.
证明:由于h=g ∗g=l1∗l1⊕l1∗g[>1]⊕g[>1]∗g, 则

由引理3知j1=i1, 故

所以

且xzs/2∈T(l1), s=1,2,··· ,k, 即g具有如下形式

命题6不但给出了一个新的必要条件, 而且当h=g ∗g时, 其还可以用于确定g的部分线性项.
3.2 h =g ∗g 的星积分解
本小节假定h=g ∗g已知, 但g ∈C∗未知, 针对两种情形分别给出了两个求取g的高效算法. 在第一类情形中, 基于对布尔函数求偏导降次的思想, 我们将g ∗g的分解问题转化为l ∗g的分解问题, 其中l是线性布尔函数, 进而利用现有的左线性星积分解算法求得g. 在第二类情形中, 我们首先构建关于布尔函数求偏导的函数方程, 然后利用按照次数进行“分层剥离” 的思想依次求取g[d], g[d−1], ··· , g[1], 从而最终求得g, 其中d=deg(g). 下面给出第一类情形的分解算法. 在引理3的基础上, 定理1 将一类g的求解问题归结为2.3 节中的左线性星积分解问题.
定理1若h=g ∗g, 且g ∈C∗满足i1≥is −is−1, s=2,3,··· ,t, 记

则有js=is, 进一步有
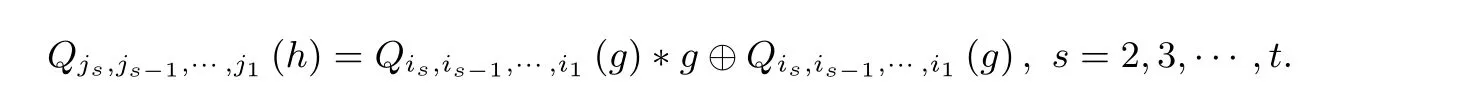
证明:在式(4)定义下, 由引理3知,s=1 时结论成立; 假设s=k时结论也成立, 则当s=k+1 时

分下面两种情况讨论:
(1) 当lk+1=0 时,jk+1=ik+1;
(2) 当lk+1̸= 0 时,jk+1= min{ik+1,minsub{lk+1}+i1}, 由于i1≥ ik+1−ik且ik 因此由上述两种情况得jk+1=ik+1. 于是, 综上, 由归纳假设可知, 结论对s=1,2,··· ,t都成立. 对上述定理1, 当s=t时, 由式(4)定义可知,Qit,it−1,···,i1(g) 为线性函数, 则由命题1-(5) 知 算法2 h=g ∗g 型的第一类分解算法Input: 非奇异特征函数h Output: h = g ∗g 对应的因子g 1 h′ ←h 2 j1 ←minsub(h[>1])3 h ←Qj1 (h)4 j2 ←minsub(h[>1])5 s ←2 6 while j1 ≥js −js−1 do 7h ←Qjs (h)8s++;9js ←minsub(h[>1])10 end 11 (l,g′) ←GetMaxOrderLeftLinearFactor(h)12 a ←ϕ(l) 中因子x 的最大重数13 L ←ϕ(l)/xa 14 b ←ord(h)/2 −ord(g′)−(a −(js −j1))15 Ω ←{L1 : L1 |L and deg{L1} = b}16 if Ω = ∅then 17g ←xa−(js−j1) ∗g′ ⊕x0 18Return g 19 end 20 for all L1 in Ω do 21L2 ←xa−(js−j1) ·L1 22g ←ϕ−1(L2)∗g′ ⊕x0 23if h′ = g ∗g then 24Return g 25end 26 end 下面先对算法2 的时间复杂度进行简要分析, 记N为h的项数,D为h的次数, 算法2 中第1 行到第10 行的时间复杂度上限为O(DN), 子函数GetMaxOrderLeftLinearFactor的时间复杂度上限为O(N), 第12 到20 行的时间复杂度相比之下可以忽略不计, 则最终算法2 的时间复杂度为O(DN). 为了便于更准确地理解算法2 的分解过程, 在本文附录1 中我们给出了详细分解示例. 当定理1 条件不满足时, 情况有些复杂, 但依然可以通过类似定理1 的求偏导来求取g. 作为准备, 我们首先给出引理4. 引理4若h=g ∗g且g ∈C∗满足i1≥is −is−1, s=2,3,··· ,k,i1+minsub(lk+1) 证明:在式(4)定义下, 由定理1 可知 这里s=2,3,··· ,t. 故s=k+1 结论成立. 综上, 根据归纳假设可知引理结论成立. 当引理5中s=t时有 根据式(4)定义可知deg(Qit,it−1,···,i1(g))=1, 下面给出定理2, 通过定理2 可唯一求解出特征函数g, 具体求解算法见算法3. 算法3 h=g ∗g 型的第二类分解算法Input: 非奇异特征函数h Output: h = g ∗g 对应的因子g 1 h′ ←h 2 j1 ←minsub(h[>1])3 h ←Qj1 (h)4 j2 ←minsub(h[>1])5 s ←2 6 while j1 ≥js −js−1 do 7h ←Qjs (h)8s++9js ←minsub(h[>1])10 end 11 h ←Qjs (h)12 if ord(h)−minsub(h) ≥ord(h′)/2 then 13Return None 14 end 15 d ←js −j1 16 h ←σ−d(h)17 由h 得到i2,i3,··· ,it; Qi2,i1 (g), ··· ,Qit,it−1,···,i1 (g)18 h ←h ⊕Qj1 (h′)19 h ←Qit,it−1,···,i2 (h)20 由h 计算出g 21 Return g 定理2对于式(6), 记l0=Qit,it−1,···,i1(g), QH=Qit,it−1,···,i3,i2(H), d= deg(QH), 则d=deg(g) 且 即g是被QH唯一确定的. 证明:由星积运算性质以及偏导数定义可知deg(g) = deg(l0∗g) =d; 且根据式(6)和定理中符号定义可知 下面按照次数分类, 得到下列等式 将上述等式移项整理则得到所证结论, 根据左线性星积分解的唯一性理论可知,g的各次项被QH唯一确定, 即g是被QH唯一确定的. 下面对算法3 的时间复杂度进行简要分析, 记N为h的项数,D为h的次数, 算法3 中第1 行到第14 行的时间复杂度上限为O(DN), 第15 行到第19 行的时间复杂度上限为O(DN), 由h计算出g的时间复杂度上限为O(DN), 则算法3 的时间复杂度为O(DN). 为了便于更准确地理解算法3 的分解过程, 在本文附录2 中我们给出了详细分解示例. 值得注意的是文献[13] 中虽然给出了分解h=f ∗g的一般算法, 但是在具体分解过程中需要合理猜测r[d−1],r[d−2],...,r[1](详见文献[13] 中的Section VI), 这使得分解算法的时间复杂度往往不可控制, 当h的阶数和项数稍大时, 分解算法往往难以给出分解结果. 本节在第3 节的基础上, 进一步给出相关结论, 主要分为三个小节. 4.1 节是在第3 节的基础上给出以非线性最大下标求偏导的结果, 作为第3 节结论的补充, 可以处理第3 节无法处理的情形; 4.2 节给出一类一般情形的分解向h=g ∗g分解的转化, 从而可以快速实现分解; 4.3 节将h=g ∗g的结论推广到h=g ∗g ∗···∗g这一情形. 对任意的n阶布尔函数f(x0,x1,··· ,xn), 记R(f(x0,x1,··· ,xn))=f(xn,xn−1,··· ,x0), 则由星积运算的定义易知如下引理6成立. 引理6若h=f ∗g, 则R(h)=R(f)∗R(g). 由引理6知若h=g ∗g, 则R(h)=R(g)∗R(g). 因此对h非线性最大下标求偏导等价于对R(h) 的非线性最小下标求偏导, 从而易得类似于第3 节的结论, 这里不再重复给出. 从分解角度看, 当h不满足第3 节的条件时, 可以直接用R(h) 进行判断是否满足条件, 不需要转化为非线性最大下标求偏导. 已有的非线性星积分解算法的计算复杂度和存储复杂度较高, 因此我们考虑一类特殊的非线性星积分解情形, 当其星积因子较为“接近” 时, 将这一类非线性星积分解转化为便于分解的g ∗g的情形, 从而降低这一类非线性星积分解的时间复杂度. 这里只考虑非平凡情形, 即h=f ∗g, 其中deg(f)>1,deg(g)>1. 证明:已知 其中(f ⊕g)∗g=(f ⊕g)[1]∗g ⊕(f ⊕g)[>1]∗g. 由f和g都是非奇异特征函数知 所以minsub((f ⊕g)[>1]∗g)>i1, 因此 根据定理3 我们可以得到当f和g较为“接近” 时, 即其满足条件minsub((f ⊕g)[>1])>i1时,h=f ∗g的分解就转化为h=g ∗g这一类型, 此时若g满足第3 节的条件, 即可求解出g, 得到右星积因子, 通过文献[13] 第VI-C 节结论可以求得左星积因子f. 上述部分主要研究h=g ∗g的情形, 其分解方法可以推广到一般的h=g ∗g ∗···∗g这一情形, 从而可以得到h=g ∗g ∗···∗g的两类分解算法. 结论推广主要利用归纳法以及引理1的结论, 将最左侧的g看作h的左星积因子, 其余的看作h的右星积因子, 记作f, 则h=g ∗f, 通过归纳和逐层求偏导即可得到推广结论, 这里不再给出. 值得注意的是,g的个数的奇偶性影响类似式(5)中的右星积因子的形式, 当其为偶数时, 右星积因子为g ⊕x0, 当其为奇数时, 右星积因子为g, 该形式对第一类算法有影响, 但最终都可以利用左线性星积分解方法求得g. 本文主要探讨h=g ∗g型特征函数的星积分解问题, 以期能为一般的星积分解问题提供借鉴和探索分解之法. 针对两类情形, 我们给出了由h=g ∗g求取g的高效算法. 在第一类情形中, 基于对布尔函数求偏导降次的思想, 我们将g ∗g的星积分解问题转化为l ∗g的星积分解问题, 其中l是线性布尔函数,然后基于现有的l ∗g分解算法高效地求得g; 在第二类情形中, 我们首先给出关于h求偏导的函数方程,然后利用按次数进行“分层剥离” 的思想依次求取g[d],g[d−1],··· ,g[1], 从而最终求取g, 其中g[k]的求取也是转化为l ∗g[k]的星积分解来实现. 此外, 本文从星积分解的角度给出了两个特征函数较为“接近” 的一种刻画, 并将较为“接近” 的特征函数的星积分解问题转化为h=g ∗g的星积分解问题. 遗憾的是, 仍然存在本文算法无法解决的情形, 因此关于h=g ∗g的进一步研究是我们下一步工作的重点. 另外, 需要进一步研究如何由h=g ∗g的星积分解探索一般的非线性星积分解. 由于j1=1, 此时 由于j2=2, 满足条件j1≥j2−j1, 此时 由于j3=4, 不满足条件j1≥j3−j2, 对Q2,1(h) 进行左线性星积分解得 此时Ω 为空集, 则 验证可知,h=g ∗g, 分解成功. 附录2第二类情形示例 已知待分解的非奇异特征函数 由于j1=1, 此时 由于j2=3, 不满足条件j1≥j2−j1, 此时 即Q1(g)=x2⊕x4x5, 因此i2=4, 且 下面按次数对g进行求解. 则Q4(Q1(h)⊕Q1(g))=x3⊕x5⊕x6x7⊕x6x9x10⊕x11=x5∗g ⊕Q4(x2∗g),故deg(g)=3, 且 解得 因此g=x0⊕x1x2⊕x1x4x5⊕x6. 验证可知,h=g ∗g, 分解成功.


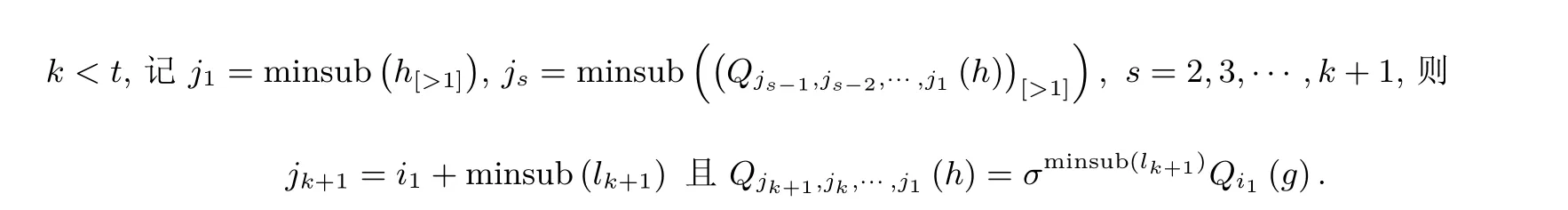




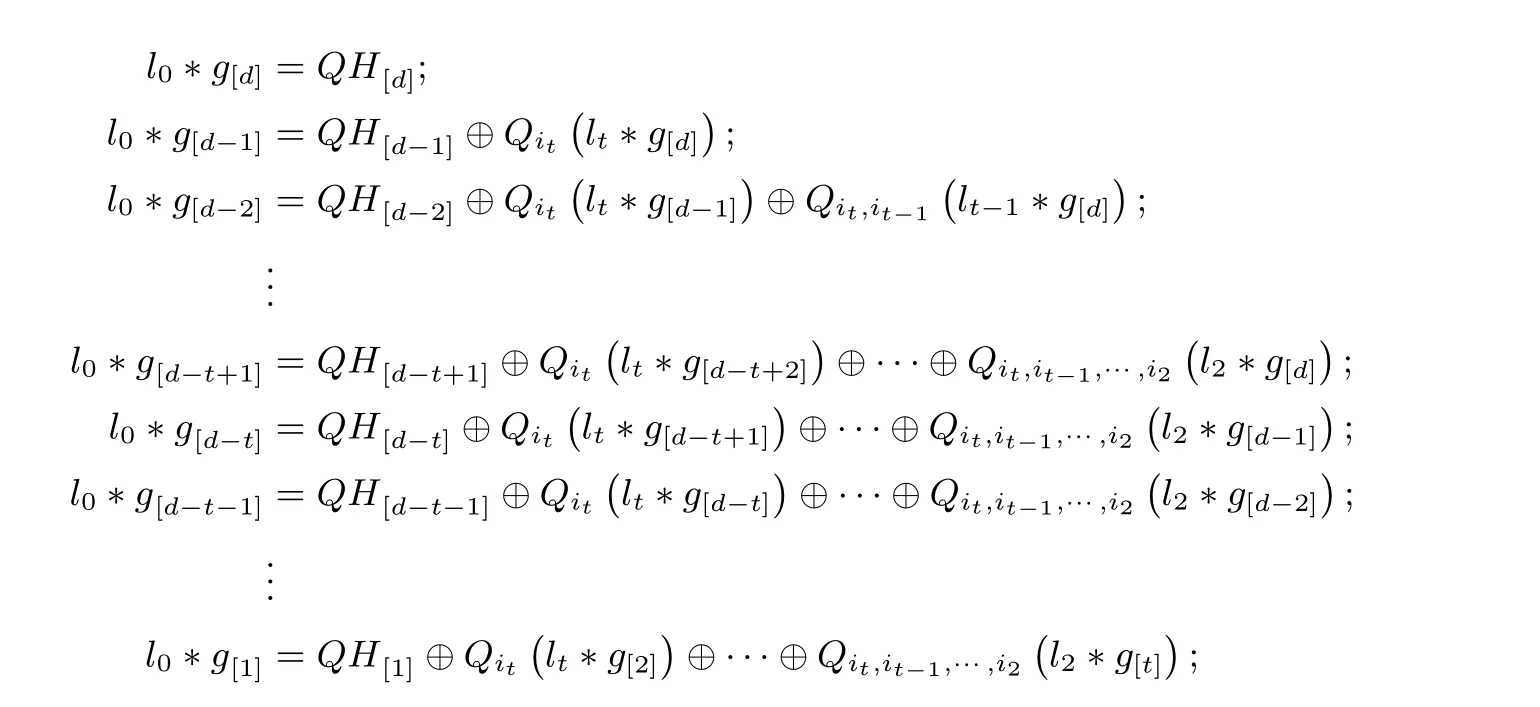
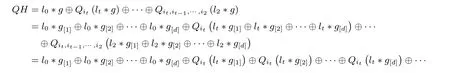


4 进一步结果
4.1 以非线性最大下标求偏导的结果
4.2 h =f ∗g 转化为h =g ∗g



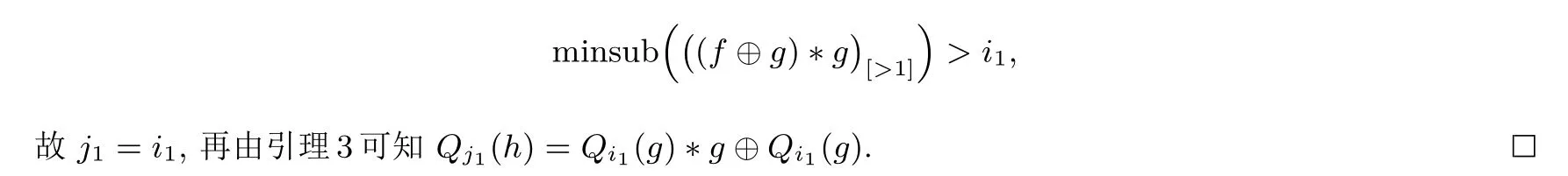
4.3 h =g ∗g ∗···∗g 的分解
5 结束语