安全高效的加密数据朴素贝叶斯训练和分类*
2022-07-13李兴鑫朱友文
李兴鑫, 朱友文,2,3, 王 箭
1. 南京航空航天大学计算机科学与技术学院, 南京 210016
2. 广西师范大学广西多源信息挖掘与安全重点实验室, 桂林 541004
3. 桂林电子科技大学广西可信软件重点实验室, 桂林 541004
1 引言
朴素贝叶斯分类是一种有效的机器学习算法, 在文本检测以及医疗诊断等领域有着重要应用[1]. 朴素贝叶斯分类算法由两个阶段组成: 训练阶段以及预测阶段. 训练阶段从标记好的训练集中训练出朴素贝叶斯分类器模型. 预测阶段利用训练好的朴素贝叶斯分类器判断样本的类标签. 通常在训练阶段需要大量的数据进行模型训练, 这会产生巨大的计算和存储负担, 因此无法在一些资源受限的设备上进行. 另一方面,一些大型组织和机构通过机器学习即服务(machine learning as a service)[2]将其训练好的机器学习模型提供给个人以及小型公司. 为了支持处理用户频繁的任务请求, 这些大型机构需要支付高昂的费用部署和维护本地设备. 随着云计算的逐渐普及, 将数据和训练分类任务外包给云服务器, 利用云强大的计算能力减轻用户本地负担, 是上述问题的一个可行解决方案. 然而外包数据中通常包含一些隐私信息, 比如个人健康或生物特征信息, 并且训练好的模型也被视为所有者的私人财产. 因此, 外包朴素贝叶斯模型训练和分类过程中的数据隐私安全问题不容忽视.
同态加密[3,4]是一种保护外包数据隐私和实现安全计算的有效方式. 用户在本地利用同态加密算法加密自身数据, 随后将加密数据外包到云服务器. 同态加密的语义安全性质能够为外包数据隐私提供强有力的保障, 同时同态性质也使得云服务器能够在加密数据上进行训练和分类所需的相关运算. 文献[5–9]借助同态加密实现了不同的安全外包机器学习算法, 比如: 加密数据安全k近邻分类和安全卷积神经网络. 但是这些方案都只适用于安全实现特定机器学习算法, 无法直接应用于实现安全贝叶斯训练和分类.
文献[10,11] 实现了分布式环境下的安全贝叶斯模型训练和分类. 这些方案中各个参与方拥有训练集的部分数据, 并能从中推测出部分参数用于贝叶斯模型训练以及进行样本分类. 这与本文考虑的外包模型有所不同, 在外包场景下为了保护数据隐私, 数据集被加密后上传到云服务器中, 因此云服务器无法从中获得明文数据的任何有效信息. 文献[7,12–14] 考虑了一方持有贝叶斯模型另一方持有待分类样本的场景,在不泄漏模型和待分类样本隐私的情况下安全运用训练好的模型对样本进行分类. 文献[7,15,16] 运用全同态加密将朴素贝叶斯模型加密后外包到云服务器, 并且基于同态性质提出了安全外包朴素贝叶斯分类方案. 这些方案均假设贝叶斯模型已经训练完成, 主要考虑的是预测阶段中如何在保护模型和待分类样本隐私的情况下完成安全贝叶斯分类计算, 无法用于实现加密数据上的安全贝叶斯模型训练. 文献[17] 提出的方案实现了从加密数据安全获取部分贝叶斯模型参数, 这些参数随后返回给一个服务器用于生成最终的贝叶斯模型. 该方案需要将训练好的贝叶斯模型泄漏给一个服务器. 文献[18] 提出的方案结合Paillier 同态加密算法和不合谋云服务器模型实现加密数据集上的贝叶斯模型安全训练和分类运算. 但是这一方案在用户端和云服务器端的计算和通信开销太高, 无法处理大规模外包数据. 与上述基于密码学方法的工作不同, 文献[19,20] 提出了(本地) 差分隐私下的安全朴素贝叶斯训练和分类方案. 虽然这些工作相比于基于密码学方法的方案具有更好的运行效率, 但其一方面会泄漏数据集或者模型的隐私给参与方, 另一方面也会造成分类准确率的损失.
本文结合somewhat 同态加密算法(SHE)、SIMD 技术和混淆电路提出了加密数据上的安全高效朴素贝叶斯训练和分类方案. 本文提出的方案对贝叶斯模型训练和分类算法进行转换并且设计了新的明文编码方式, 从而避免了计算过程中在密文上进行除法运算以及中间结果溢出问题. 基于两个不合谋云服务器模型、SHE 的同态性质和SIMD 技术, 本文提出了一系列交互协议批量地在加密数据上实现了外包朴素贝叶斯训练和分类阶段所需的安全类标签频数计算和待分类样本频数统计, 并且通过结合混淆电路提出了加密数据安全类标签判断协议. 本文在半诚实模型下分析了提出方案的安全性. 提出方案能够保护外包数据集、朴素贝叶斯分类器模型、待分类样本以及分类结果的隐私. 通过实验对提出方案的性能进行了评估, 实验结果表明本文方案与目前最新的安全朴素贝叶斯训练和分类方案[18] 相比具有更好的运行效率.
2 预备知识
2.1 符号描述
论文中的符号标记和描述显示在表1 中.

表1 符号描述Table 1 Notations
2.2 朴素贝叶斯分类器
假定存在一个包含n个已标记样本的数据集D={q1,q2,··· ,qn}, 所有类标签的集合为CL ={l1,l2,··· ,lλ}. 每个样本qi(i ∈[1,n]) 有d个属性可以看成一个d维向量qi=(qi1,qi2,··· ,qid), 并且对应的类标签为Ci ∈CL. 给定一个待分类样本S= (S1,S2,··· ,Sd), 朴素贝叶斯分类器根据最大后验概率预测样本S的类标签CS ∈CL, 也即
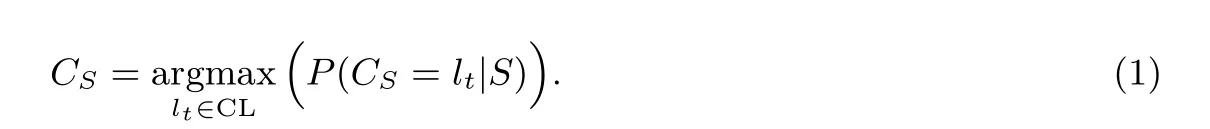
由贝叶斯定理可知
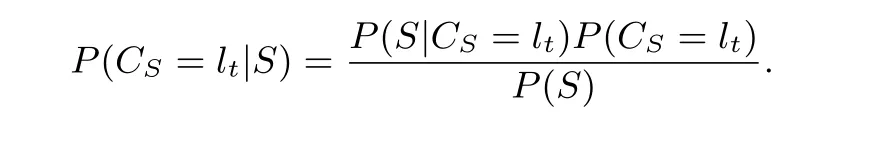
在上述公式中,P(S) 对于不同的后验概率都是相同的, 因此公式(1)可以转换为
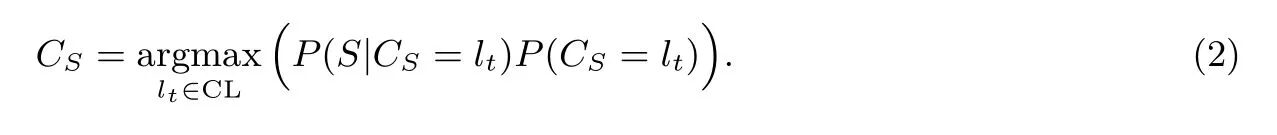
在朴素贝叶斯分类器中假设样本的属性之间是相互独立的, 因此可得
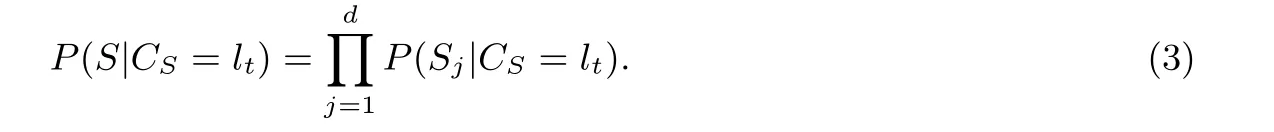
进一步将类标签判断转换为
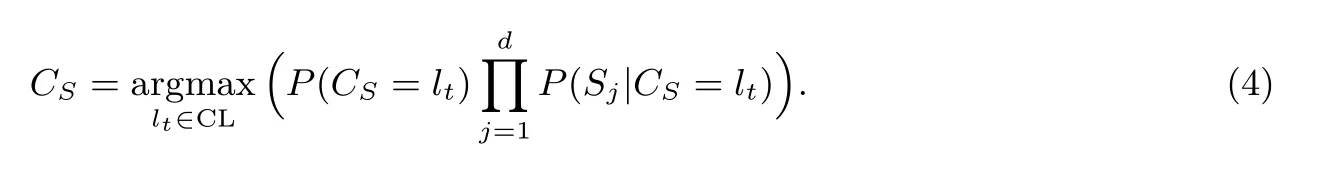
在公式(4)中, 概率P(CS=lt) 和P(Sj|CS=lt) 通过如下公式从训练集D中计算获得.
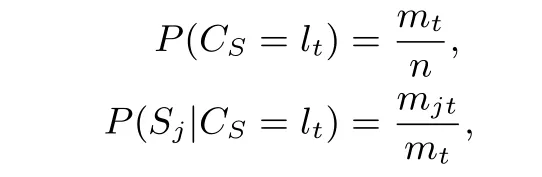
其中n是D中样本的个数,mt表示训练集D中类标签为lt(t ∈[1,λ]) 的样本个数,mjt表示D中类标签为lt并且第j(j ∈[1,d]) 个属性值等于Sj的样本个数.

2.3 Somewhat 同态加密
Somewhat 同态加密(SHE) 是一种公钥加密系统, 能够实现密文上任意数量的同态加法运算和有限次的同态乘法运算. 本文采用文献[21] 提出的算法作为SHE 的实现方案. 这一方案的明文空间是一个多项式环Rp=Zp[x]/Φu(x), 其中p是一个大素数, Φu(x) 是u阶的分圆多项式. Somewhat 同态加密系统包括: 密钥生成算法(SHE.Gen)、加密算法(SHE.Enc) 以及解密算法(SHE.Dec). SHE.Gen 是一个概率算法, 接收安全参数u、p以及L作为输入, 输出一个公私钥对(pk,sk). 这里u和p决定明文空间,L决定somewhat 同态加密能够支持的同态乘法的深度. SHE.Enc 是一个概率算法, 接收pk 和明文m作为输入, 输出密文Epk(m). SHE.Dec 是一个确定性算法, 输入为密文Epk(m) 和私钥sk, 输出为明文m.SHE 是语义安全的并且具有如下的同态性质:
同态加法: 给定两个密文Epk(x) 和Epk(y), 存在运算⊞使得Epk(x+y)=Epk(x)⊞Epk(y). 给定一个密文Epk(x) 和一个公开的常数a,Epk(x+a)=Epk(x)⊞a.
同态乘法: 给定两个密文Epk(x) 和Epk(y), 存在运算⊠使得Epk(xy) =Epk(x)⊠Epk(y). 给定密文Epk(x) 和公开常数a,Epk(ax)=Epk(x)⊠a.

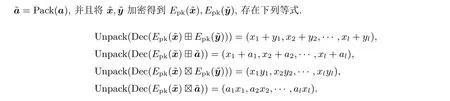
2.4 混淆电路
对于任意函数f, 混淆电路(garbled circuits) 允许两个参与方在不泄漏各自持有数据x和y的情况下安全计算函数值f(x,y). 混淆电路的核心思想是一方(记为电路生成方) 先对函数f所对应的布尔电路和自己的输入x加密, 并将加密的布尔电路和输入发送给另一方(电路计算方). 电路计算方与电路生成方交互获得自身输入y的加密值, 随后结合收到的x的加密值在加密布尔电路上进行运算. 最终双方能够在不获得对方输入有效信息的情况下计算得到函数值f(x,y).
混淆电路已经被证实在半诚实模型下是安全的, 并且能够高效处理非线性运算操作[23]. 本文中主要运用混淆电路进行比较操作, 这需要用到一个比较混淆电路(CMP). CMP 的线路和功能描述如下: 给定两个σ比特的输入x,y, CMP 安全比较x和y的大小, 输出1 如果x 如图1 所示, 本文提出方案的系统模型由多个数据拥有者DO、云服务器CS1和CS2以及用户Usr组成. 每个数据拥有者DOi持有部分数据集Di并希望通过云服务器聚合数据进行训练以提供更精确的朴素贝叶斯分类器. 为了保护外包数据的隐私, DOi选择在本地加密自身数据集. 为此云服务器CS2生成SHE 同态加密的公私钥(pk,sk) 并发布公钥pk. DOi利用pk 加密自身数据集Di并将加密数据集Epk(Di) 上传到云服务器CS1. 用户Usr 持有样本S, 利用公钥pk 加密样本并发送Epk(S) 给云服务器CS1. 在收到加密样本Epk(S) 后, CS1与CS2从加密数据集Epk(D) 中训练得到朴素贝叶斯分类器模型的参数并且安全地判断样本S的类别. 由于Usr 无法接触到私钥sk, 本文通过如下方式将分类结果返回给Usr. CS1向加密类标签Epk(CS) 添加随机数, 并将扰动的结果发送给CS2. 随后CS1将随机数返回给Usr, CS2解密收到的加密数据并返回给Usr. 在收到两个云服务器发送的数据, Usr 能够从中恢复得到最终的分类结果CS. 图1 安全朴素贝叶斯方案系统模型Figure 1 System model 在本文模型中, 数据拥有者DO 是诚实的, 并且用户Usr 与数据拥有者之间也是相互信任的. 本文方案中DO 和Usr 只需要加密自身数据并将其上传至云服务器, 此后并不参与后续的计算, 所有计算任务都由两个云服务器CS1和CS2交互完成. 这种方式能够显著地减少DO 和Usr 的计算负担. 在设计安全外包方案时主要考虑的攻击者是两个云服务器CS1和CS2. 本文假设两个云服务器CS1和CS2是半诚实的[24]并且是不合谋的. 这种不合谋假设已经被现有的许多工作[5]所采用, 在现实应用中也是比较实用的假设. 可以将两个云服务器分别部署在不同的云服务器提供商中, 比如: Amazon 和阿里云, 这些大型的IT 公司出于商业信誉的考虑一般不会相互合谋. 半诚实模型的定义描述如下: 定义1令f(x,y) 是一个计算函数,f1(x,y) 和f2(x,y) 分别表示f(x,y) 第一部分和第二部分. Π 是计算f(x,y) 的一个两方协议, View1(x,y) 和View2(x,y) 分别是两个参与方执行协议Π 过程中的视图.View1(x,y) = (x,r,M1,M2,··· ,Mt), View2(x,y) = (y,r,M1,M2,··· ,Mt), 其中x和y分别代表两个参与方的输入,r表示随机数,Mi表示在协议执行过程中收到的第i个消息. Π 安全地计算了函数f, 也即Π 在半诚实模型下是安全的, 如果存在多项式时间内的模拟器S1和S2使得 3.4.1 安全批量乘法协议 协议1 安全批量相等判断协议(SBEP)Input: CS1 持有密文Epko(˜x),Epko(˜y), CS2 持有解密密钥sko Output: CS1 获得Epko(˜z) 满足zi = 1 如果xi = yi; 否则zi = 0 (i ∈[1,l])1 CS1 选取一个随机数向量r = (r1,r2,··· ,rl) ∈Zlpo, 计算Epko(˜u) = Epko(˜x)⊞(−Epko(˜y))⊞Pack(r)并将其发送给云服务器CS2.2 CS2 解密得到u = (u1,u2,··· ,ul) ∈Zl po.3 for i = 1 to l do 4CS2 将ui 分解成比特(u(σ−1)i,u(σ−2)i,··· ,u(0)i ), 其中σ 是模数po 的比特长度.5CS1 同时将ri 分解成比特(r(σ−1)i,r(σ−2)i,··· ,r(0)i ).6 end 7 for j = 0 to σ −1 do 8CS2 将向量u(j) = (u(j)1 ,u(j)2 ,··· ,u(j)l ) 打包成˜u(j), 加密得到Epko(˜u(j)), 将其发送给CS1.9CS1 计算v(j) = Pack(1)⊞(−(Epko(˜u(j))⊞Pack(r(j)1 ,r(j)2 ,··· ,r(j)l )⊞(−2Pack(r(j)1 ,r(j)2 ,··· ,r(j)l )⊠Epko(˜u(j)))),其中1 是长度为l 的全1 向量.10 end 11 CS1 和CS2 调用SBMP 对σ 个密文v(0),v(1),··· ,v(σ−1) 安全相乘, 得到Epko(˜z) = SBMP(v(0),v(1),··· ,v(σ−1)). 这一过程中的SBMP 只需要在一个密钥对(pko,sko) 上运算. 3.4.3 安全比较协议 安全比较协议(SCP) 中CS1拥有E(x),E(y) 其中0≤x,y y; 否则输出θ=E(0). 由于0≤x,y y;否则z0=0. CS1随后选取一个随机数r ∈Zp计算E(v)=E(z)⊞r并将E(v) 发送给CS2. 这里v=z+rmodp, 并且z0=β ⊕r0⊕v0其中β是(v 本文提出的安全朴素贝叶斯方案由以下几个阶段组成. 在这一阶段中, 云服务器 CS2从数据拥有者 DO 处获得数据集D中样本的总个数n, 每一个样本的属性个数d以及所有类标签 CL ={l1,l2,··· ,lλ}, 并确定系统所需的明文空间模数p1,p2,··· ,ph. 随后CS2利用SHE 同态加密的密钥生成算法Gen 输入参数u、pi以及L, 生成公私钥对{pki,ski}1≤i≤h. 同时CS2生成系统的扩展因子γ用于将浮点数转化为整数. 最后CS2发送公共系统参数n,d,CL,u,{pi}1≤i≤h,L给其它参与方. CS2发送公钥{pki}1≤i≤h给CS1, 从公钥集合{pki}1≤i≤h中随机选取一个公钥pko(o ∈[1,h]) 发送给数据拥有者DOs 和用户Usr 用于加密数据集和待分类样本. 这一阶段中各个数据拥有者DO 利用SHE 同态加密和SIMD 技术对各自的数据集加密, 并将加密的数据集上传到云服务器CS1中. 这里以数据集D被一个数据拥有者DO 持有为例说明数据集的加密过程. 详细的数据集加密过程显示在协议2 中. 在加密过程中DO 首先用扩展因子γ对每个样本数据扩展取整, 并将每一个样本的类标签Ci转换成一个0,1 向量ci满足如果Ci=lt则ci中第t位为1, 其余位都为0. 随后DO 将数据集D划分成s个数据块, 每个数据块中包含l个样本. 假设样本总数n是l的倍数. 对于每一个数据块i, DO 将同一属性j下的l个数据记录打包在一起并用公钥pko对其加密得到Aij. 同时DO 也加密数据块i中每个样本对应的类标签得到Cit. 最终DO 得到加密数据集Epko(D)并将其发送给CS1. 本文方案可以稍微改动以支持数据集D水平分布以及垂直分布在多个DO 的情况. • 如果D水平分布在各个数据拥有者, 也即每个数据拥有者DOi持有部分数据集Di, 其中包含ni个样本的全部属性和相应的标签. 数据集Di加密的步骤与协议2 相同, 只需要将n换成ni. • 如果D垂直分布在各个数据拥有者, 每个数据拥有者DOi持有数据集D全部样本的部分属性di. DOi加密Di时, 需将协议2 中的d换成自己持有属性di. 此外只由持有样本类标签的数据拥有者需要加密每个样本的类标签. 协议2 数据集加密Input: 数据拥有者持有明文数据集D 和公钥pko Output: CS1 获得加密数据集Epko(D)1 DO 执行如下操作:2 for i = 1 to n do qij = ⎿γqij」.5end 6将Ci 转换成λ 维向量ci. 对于t ∈[1,λ], 如果Ci = lt, cit = 1, ci 其余部分全部为0.7 end 8 for i = 1 to s = n/l do 3for j = 1 to d do 4 9计算k = (i −1)∗l+1.10for j = 1 to d do 11˜qij = Pack(qk,j,qk+1,j,··· ,qk+l−1,j), Aij = Epko(˜qij).12end 13for t = 1 to λ do 14˜cit = Pack(ck,t,ck+1,t,··· ,ck+l−1,t), Cit = Epko(˜cit).15end 16 end 17 发送加密数据集Epko(D) = {Aij,Cit}1≤i≤s,1≤j≤d,1≤t≤λ 给云服务器CS1.18 CS1 获得加密数据集Epko(D). 协议3 安全类标签频数计算Input: CS1 持有加密数据集的类标签{Cit}1≤i≤s,1≤t≤λ, CS2 持有私钥(ski)1≤i≤h Output: CS1 获得E( ˜md−1)1 for t = 1 to λ do 3 CS1 选择随机比特向量bit ∈Zl2, 计算发送Epko(˜uit) = Cit ⊞˜bit ⊞(−2˜bit ⊠Cit) 给CS2.2for i = 1 to s do 4 CS2 用私钥sko 解密Epko(˜uit) 得到uit.5 CS2 计算发送E(˜uit) = {Epk1(˜uit),Epk2(˜uit),··· ,Epkh(˜uit)} 给CS1.CS1 计算C′it = E(˜u)⊞˜bit ⊞(−2˜bit ⊠E(˜u)).7end 8CS1 计算E(˜vt) = C′1t ⊞C′2t ⊞···⊞C′st.9CS1 选择随机向量rt ∈Zlp, 计算E(˜vt + ˜rt) = E(˜vt)⊞˜rt 并发送给CS2.10CS2 解密得到vt +rt, 并计算τt = ∑lk=1(vtk +rtk).6 11 end 12 CS2 将τ = (τ1,τ2,··· ,τλ) 打包成˜τ, 发送密文E(˜τ) 给CS1.13 CS1 计算E( ˜m) = E(˜τ)⊞Pack(−∑l k=1 r1k,··· ,−∑l k=1 rλk).14 CS1 和CS2 执行SBMP 获得E( ˜md−1) =SBMP(E( ˜m),E( ˜m),··· ,E( ˜m)). 协议4 安全待分类样本频数统计Input: CS1 持有加密数据集Epko(D) 和加密待分类样本Epko(˜S), CS2 持有私钥(skw)1≤w≤h Output: CS1 获得E(˜µ) 其中µt = ∏d j=1 mjt (t ∈[1,λ])1 for j = 1 to d do 2for i = 1 to s do CS1 与CS2 运行SBEP 得到Epko(˜xij) = SBEP(Aij,Epko(˜Sj)).4end 5 end 6 for j = 1 to d do 3 7for t = 1 to λ do 8 for i = 1 to s do CS1 计算Epko(˜yijt) = Epko(˜xij)⊠Cit.10CS1 选择随机比特向量bijt ∈Zl2, 计算发送Epko(˜zijt) = Epko(˜yijt)⊞˜bijt ⊞(−2˜bijt ⊠Epko(˜yijt)) 给CS2.11CS2 解密得到˜zijt, 发送E(˜zijt) = {Epk1(˜zijt),Epk2(˜zijt),··· ,Epkh(˜zijt)} 给CS1.12CS1 计算E(˜yijt) = E(˜zijt)⊞˜bijt ⊞(−2˜bijt ⊠E(˜zijt)).13end 14CS1 计算E(˜ejt) = E(˜y1jt)⊞E(˜y2jt)⊞···⊞E(˜ysjt).15CS1 选择随机向量rjt ∈Zlp, 计算E(˜ejt + ˜rjt) = E(˜ejt)⊞˜rjt 并发送给CS2.16CS2 解密得到ejt +rjt, 并计算fjt = ∑lk=1(ejt[k]+rjt[k]).9 17end 18CS2 将fj = (fj1,fj2,··· ,fjλ) 打包成 ˜fj, 发送密文E( ˜fj) 给CS1.19CS1 计算E(˜gj) = E( ˜fj)⊞Pack(−∑l k=1 rj1[k],··· ,−∑l k=1 rjλ[k]).20 end 21 CS1 和CS2 计算E(˜µ) = SBMP(E(˜g1),E(˜g2),··· ,E(˜gd)). 协议5 安全类标签判断Input: CS1 持有加密数据E(˜µ) 和E( ˜md−1), CS2 持有私钥(skw)1≤w≤h Output: Usr 获得样本S 的类标签CS 1 CS1 选取随机数向量r,R ∈Zλp, 计算E(˜µ)⊞˜r 和E( ˜md−1)⊞˜R 发送给CS2.2 CS2 用私钥{skw}1≤w≤h 解密得到µ+r 和md−1 +R.3 for t = 1 to λ do 4CS2 加密得到E(µt +rt) 和E(md−1 t+Rt) 发送给CS1.5CS1 计算E(µt) = E(µt +rt)⊞(−rt) 和E(md−1t ) = E(md−1t+Rt)⊞(−Rt).6 end 7 CS1 设置E(idx) = E(1), α = E(µ1), β = E(md−11 ). for t = 2 to λ do 8CS1 计算得到α ⊠E(md−1 t ) 和β ⊠E(µt), 并和CS2 执行SCP 协议得到θ = SCP(α ⊠E(md−1 t ),β ⊠E(µt)).9CS1 计算E(idx) = t ⊞(θ ⊠(E(idx)⊞(−t))),α = E(µt)⊞(θ ⊠(α ⊞E(−µt))),β = E(md−1t )⊞(θ ⊠(β ⊞E(−md−1t ))).10 end 11 CS1 选取随机数a ∈Zp, 计算E(idx)⊞a. CS1 发送E(idx)⊞a 给CS2, a 给用户Usr.12 CS2 解密E(idx)⊞a 得到idx+a, 发送idx+a 给Usr.13 Usr 收到CS1 和CS2 的数据后计算得到idx, 设置样本的类标签为CS = lidx. 在本文提出的方案中, 数据拥有者DO 加密数据集上传到云服务器后不再参与后续安全朴素贝叶斯分类计算, 用户Usr 仅仅加密待分类样本发送给云服务器并从云服务器接收样本的分类结果. 两个不合谋的云服务器CS1和CS2通过运行设计的交互协议实现安全朴素贝叶斯训练和分类计算. 因此本文考虑CS1和CS2是潜在的攻击者, 并证明提出方案在运行过程中不会泄漏隐私信息给半诚实的CS1和CS2.半诚实模型的安全性定义显示在定义1中. 本节首先证明提出的安全原语SBMP、SBEP 和SCP 在半诚实模型下是安全. 定理1安全批量乘法协议SBMP 在半诚实模型下是安全的, 不会泄漏任何有效信息给CS1和CS2. 定理2提出的安全批量相等判断协议SBEP 在半诚实模型下是安全的, 不会泄漏任何有效信息给CS1和CS2. 证明:SBEP 协议中调用了SBMP 协议, 已经在定理1 中证明了其安全性, 因此这里分析SBEP协议中除去SBMP 协议部分CS1和CS2的视图. CS1的视图为View1={pko,Epko(˜x),Epko(˜y),r,Epko(˜u),{Epko(˜u(j))}0≤j≤σ−1,{v(j))}0≤j≤σ−1,Epko(˜z)}. 可以看出CS1的视图中包含的是SHE 同态加密的密文和选取的随机数. 因此能够构造出一个与View1计算不可区分的模拟器S1. CS2的视图为View2={pko,sko,Epko(˜u),u,{Epko(˜u(j))}0≤j≤σ−1}. View2中除去u都是SHE 同态加密的密文.u是被随机向量r扰动的, 与随机数是计算不可区分的. 可以构造出一个与View2计算不可区分的模拟器S2. 综上所述, SBEP 在半诚实模型下是安全的, 不会泄漏任何有效信息给CS1和CS2. 定理3提出的安全比较协议SCP 在半诚实模型下是安全的, 不会泄漏任何有效信息给CS1和CS2. 综上所述, 安全类标签频数计算阶段在半诚实CS1和CS2模型下是安全, 不会泄漏数据集D和朴素贝叶斯分类器的隐私信息. 定理5安全待分类样本频数统计阶段在半诚实CS1和CS2模型下是安全, 不会泄漏数据集D、待分类样本S和朴素贝叶斯分类器的隐私信息. 定理6安全类标签判断阶段在半诚实CS1和CS2模型下是安全, 不会泄漏数据集D、待分类样本S、朴素贝叶斯分类器以及分类结果CS的隐私信息. 综上所述, 安全类标签判断阶段在半诚实CS1和CS2模型下是安全, 不会泄漏数据集D、待分类样本S、朴素贝叶斯分类器以及分类结果CS的隐私信息. 这一节分析提出方案的计算和通信复杂度. 主要考虑方案中计算开销比较大的运算: (1) 加密(Enc);(2) 解密(Dec); (3) 密文同态乘(Mul); (4) 明密文同态乘(Pml); (5) 密文同态加(Add); (6) 混淆电路中非异或门数目. 与其它运算比如打包、明文密文相加以及相乘相比, 这些运算的计算开销较大, 决定了提出方案的运行效率. 同样在统计通信开销时, 只考虑传输的密文(Ctx) 个数. 提出方案中每个阶段的计算和通信复杂度显示在表2 中, 详细的分析过程描述如下. 表2 本文方案计算和通信复杂度Table 2 Computational and communication cost of proposed scheme 数据集加密阶段中数据拥有者DO 将数据集分为s=n/l个数据块, 并对每一数据块的每个属性和和标签分别加密, 总共需要O(s(d+λ))Enc 运算, 上传到云服务器CS1的数据量为O(s(d+λ)) Ctx. 在安全类标签频数计算阶段, CS1和CS2需要O(hsλ) Pml、O(hsλ) Add、O(sλ) Dec 和O(hsλ)Enc 计算{}1≤i≤s,1≤t≤λ,这一过程CS1和CS2的通信为O(hsλ)Ctx. 随后通过O(hsλ)Add、O(hλ)Dec 和O(h) Enc 计算得到E(˜m), 通信量为O(hλ) Ctx. 通过调用SBMP 协议计算E(), 这需要O(hd) Pml、O(hd) Add、O(hd) Enc 和O(hd) Dec 并且CS1和CS2通信量为O(hd) Ctx. 因此安全类标签频数计算阶段需要O(h(sλ+d)) Enc、O((s+h)λ+hd) Dec、O(h(sλ+d)) Pml、以及O(h(sλ+d))Add 运算. CS1和CS2通信量为O(h(sλ+d)) Ctx. 表3 显示了本文方案和现有工作的对比分析, 详细的分析描述如下. 文献[10,14] 实现了分布式环境下的安全贝叶斯模型分类, 但这些方案中各个参与方能够接触到训练集的明文数据, 因此无法应用于外包环境. 文献[16] 实现了安全外包朴素贝叶斯分类, 但这一方案不仅需要用户和云服务器进行多轮的交互,而且运算过程中会泄漏贝叶斯模型的部分信息给用户. 文献[15] 在[16] 的基础上进一步保护了贝叶斯模型的隐私. 然而文献[15] 和[16] 均假设贝叶斯模型已经预先训练完成, 没有实现朴素贝叶斯训练阶段的安全外包. 文献[17] 提出的方案在外包环境下实现了加密数据上的贝叶斯模型训练, 但该方案泄漏了训练完成的贝叶斯模型给云服务器. 文献[20] 采用本地差分隐私构建了隐私保护朴素贝叶斯分类方案, 但这一方案同样将贝叶斯模型泄漏给了服务器. 现有工作中只有文献[18] 提出的方案实现了与本文方案相同的功能, 保护贝叶斯模型的同时在加密数据上实现训练和分类过程, 但这一方案的计算和通信开销较高. 本文结合SHE、SIMD 和混淆电路提出了安全外包朴素贝叶斯训练和分类方案, 克服了现有工作的不足, 保护外包数据和模型隐私的同时高效实现了朴素贝叶斯训练和分类过程. 后续通过实验将本文方案与实现相同功能的文献[18] 提出的方案进行性能对比, 验证了本文方案的高效性. 表3 本文方案与现有工作对比分析Table 3 Comparative analysis between proposed scheme and existing works 本节通过不同的实验来评估提出方案的性能并将其与现有工作进行对比. 我们主要与文献[18] 提出的方案进行对比. 据我们所知, 现有工作中只有这个方案实现了与本文方案相同的设计目标, 同时实现了加密数据上朴素贝叶斯分类器的安全训练和分类. 实验中假设只存在一个DO 拥有外包数据集, DO 和Usr 是配置为Intel CoreTMi5-8259U CPU@2.3 GHz 和8 GB 内存的笔记本电脑,云服务器CS1和CS2是配置为Intel CoreTMi3-3220 CPU @ 3.3 GHz 和16 GB 内存的两个台式机. 这些设备运行Ubuntu 16.04 LTS 系统并且连接在一个局域网中. 实验采用Python 语言, 使用SEAL-Python 库1https://github.com/Huelse/SEAL-Python实现SHE, 使用Gabes 库2https://github.com/nachonavarro/gabes来实现混淆电路. 实验采用缩放后的数据集Shuttle3https://www.csie.ntu.edu.tw/ cjlin/libsvmtools/datasets/multiclass/shuttle.scale, 包含57 000 个已标记样本和7 个类标签(λ=7), 每个样本有9 个属性. 实验首先测试了不同扩展因子γ对与朴素贝叶斯分类器准确率的影响. 为此设置数据集中70% 的数据为训练集, 30% 的数据为训练集. 运用不同γ对样本的属性值放大取整, 随后构建分类器测试分类准确率. 实验结果显示γ ≥105时, 放大取整数据集上构建的分类器准确率与原始朴素贝叶斯分类器准确率基本一致. 因此, 本文后续的实验中设置γ=105, 用于将样本属性值放大取整变为整数. 实验测试了在不同数据集样本数目n和样本属性d下提出方案各个阶段所需的运行时间和通信开销.实验中n选取为l= 8192 的整数倍, 从而方便对数据集进行打包运算. 数据集加密阶段、安全类标签频数计算阶段和安全待分类样本频数统计阶段的实验结果显示在图2、图3和图4. 图2 数据集加密阶段所需计算和通信开销Figure 2 Computational and communication costs of dataset encryption stage 图3 安全类标签频数计算阶段所需计算和通信开销Figure 3 Computational and communication cost of secure class label count stage 图4 安全待分类样本频数统计阶段所需计算和通信开销Figure 4 Computational and communication cost of secure smple count stage 数据集加密阶段在数据拥有者DO 端进行运算, DO 将外包数据集进行编码和加密. 从图2 中可以看出数据集加密阶段的计算和通信开销随着n和d的增加线性增长, 比如: 固定d= 3,n从8192 增加到49 152 时, 数据集加密阶段的计算时间从0.12 秒变为0.7 秒, 通信开销从2.41 MB 增长到14.42 MB;d=9 时, 随着n的增加, 数据集加密阶段的计算时间从0.19 秒变为1.14 秒, 通信开销从3.84 MB 增长到23.04 MB. 此外, 与其余阶段的实验结构对比可知数据集加密阶段的计算和通信开销相对较小. 实验结果表明提出方案在DO 端产生较低的计算通信负担. 安全类标签频数计算发生在云服务器CS1和CS2之间, 通过打包的方式安全批量计算出加密数据集中每个类标签的数目以及相应的d −1 次幂. 从图3 可以观察到这一阶段的计算和通信开销同样与n和d成线性相关. 例如: 当d= 9 时, 随着n从8192 增加到49 152, 安全类标签频数计算阶段的计算时间从5.99 秒变为12.98 秒, 通信开销从123.65 MB 增长到241.15 MB. 此外, 可以从图3(a) 和图3(c) 中观察到, 在不同d下, 这一阶段的计算时间和通信量随着n的增长幅度基本一致; 同样从图3(b) 和图3(d) 可以观察到, 在不同n下, 这一阶段的计算时间和通信量随着d的增长幅度基本一致. 这主要是由于固定了h和λ, 这一阶段的计算和通信复杂度变为O(s+d) 其中s=n/l, 因此变化n和d不会改变安全类标签频数计算阶段计算时间和通信量的增长幅度. 在安全类标签判断阶段中, 云服务器CS1与CS2根据安全类标签频数计算阶段和安全待分类样本频数统计阶段的输出E(˜md−1) 和E(˜µ) 进行计算和比较, 得到待分类样本类标签所对应索引idx 的密文并返回给用户Usr. 这一阶段的计算和通信开销与明文空间模数的个数h和外包数据集中的类标签个数λ有关. 实验中由于固定了h= 13 和λ= 7, 在不同n和d下这一阶段的运行时间固定为28.14 秒, 通信量固定为91.58 MB. 综上所述, 实验结果与5.2 节的理论分析一致: 提出方案的计算和通信开销与外包数据集大小n和样本属性d线性相关. 此外, 能够从实验结果中观察到本文方案将开销大的计算任务都外包给了云服务器CS1与CS2, 用户端的计算和通信开销较小. 我们还将本文提出方案与文献[18] 提出的方案进行对比. 文献[18] 通过Paillier 同态加密算法设计了加密数据安全贝叶斯模型训练和分类协议, 实现了与本文相同的功能. 由文献[18] 中的理论分析可知其计算和通信开销同样随外包数据集大小n和样本属性个数d的增加线性增长. 实验设置n= 8192 和d=3, 分别测量数据拥有者DO 和云服务器CS1和CS2的计算和通信开销. 本文方案中数据拥有者DO计算和通信开销主要发生在数据集加密阶段, 云服务器的计算和通信开销发生在其余三个阶段包括: 安全类标签频数计算阶段、安全待分类样本频数统计阶段和安全类标签判断阶段. 实验中采用较小的n和d主要是由于文献[18] 提出的方案的计算开销太高, 只能在规模较小的数据集上完成运算. 实验采用Paillier库4https://python-paillier.readthedocs.io/en/develop/实现Paillier 同态加密算法, 设置Paillier 加密算法的密钥长度为1024 比特. 实验结果显示在表4 中. 表4 本文提出的安全朴素贝叶斯模型方案与文献[18] 性能对比Table 4 Performance comparison between proposed scheme and Ref. [18] 从表中可以看出, 文献[18] 提出的方案中数据拥有者DO 需要470.89 秒加密外包数据集, 云服务器CS1和CS2需要4298.84 秒完成加密数据安全贝叶斯模型训练和分类, 而本文方案完成相应任务所需的时间分别为0.12 秒和45.57 秒. 相比较于文献[18], 本文方案在DO 端实现了3924.08 倍的计算效率提升, 在云服务器端实现了94.33 倍的计算效率提升. 考虑到现实场景中, DO 通常是资源受限的用户并且希望通过外包来减少本地的计算负担. 本文方案在DO 端的低计算负担显然更符合外包计算的需求. 对于通信开销, 本文方案中DO 和云服务器CS1之间仅需2.41 MB, 云服务器CS1和CS2之间需要372.24 MB. 文献[18] 中方案相应的通信开销为7.94 MB 和517.81 MB, 也同样大于本文方案. 实验结果表明,相比于现有工作, 本文提出的加密数据安全贝叶斯模型训练和分类方案有效降低了外包加密数据集上进行贝叶斯模型训练和分类的开销. 这主要是由于本文通过结合SHE 和SIMD 打包技术设计的交互协议能够批量地对外包数据进行处理计算, 而文献[18] 需要对单个数据进行加密和计算, 从而产生了较高的计算和通信成本. Vaidya 等人[10]运用安全多方计算中的安全求和协议和安全lnx运算协议设计了水平分布数据集下的安全朴素贝叶斯分类方案. 文献[11] 运用基于秘密分享的协议设计了水平分布、垂直分布以及任意分布数据集下的安全贝叶斯模型训练以及分类方案. 这些方案主要考虑的是分布式场景, 参与方可以接触到部分的明文数据集, 无法直接应用于外包环境中的安全朴素贝叶斯分类. Bost 等人[12]运用加法同态加密设计了一个加密数据安全朴素贝叶斯分类方案. 在他们的方案中, 服务器端拥有朴素贝叶斯分类模型, 用户拥有待分类的样本. 为了实现安全贝叶斯分类, 服务器运用加法同态加密将贝叶斯分类器加密发送给用户. 用户在收到加密贝叶斯模型后, 利用加同态的性质计算不同类标签下待分类样本概率的密文. 随后通过安全比较协议用户能够从加密的概率中获得分类结果. 许多后续的工作如文献[13,14,29,30] 考虑了这一用户服务器模型下的安全贝叶斯分类问题. 文献[13] 结合加法同态加密、茫然传输和提出的双重扰动技术设计了能够抵抗替代比较攻击的安全贝叶斯分类方案. Gao 等人[14]设计了一个MAS 加密框架并将其应用于安全朴素贝叶斯分类, 减少了用户和服务器之间的交互次数, 提升了文献[12] 中方案的运行效率. 这些方案[12–14,30]均假设贝叶斯模型已经被训练完成并且参与方能够接触到贝叶斯模型或者待分类样本. Khedr 等人[7]利用全同态加密算法设计了外包环境下的安全贝叶斯分类方案. 在提出方案中训练好的贝叶斯模型参数被全同态加密算法加密后上传到云服务器. 当进行分类时, 用户在本地先映射样本的每个属性使之对应模型中的概率并加密映射后的样本上传到服务器中. 云服务器利用全同态加密的性质计算样本在每个类别下概率的密文返回给用户. Sun 等人[16]进一步结合全同态加密和SIMD 技术提出了安全外包朴素贝叶斯分类方案, 减少了运算所需的计算和通信开销. 然而这两个方案需要云服务器与用户多次交互进行比较获得分类结果, 并且比较过程中会泄漏贝叶斯模型的有效信息给云服务器. 文献[15] 运用全同态加密和两个云服务器模型提出了安全外包朴素贝叶斯分类方案, 在实现分类计算的同时保护了外包贝叶斯模型的隐私. 此外上述方案均假设贝叶斯分类模型已经在本地训练完成, 仅仅实现了贝叶斯分类阶段的外包. Liu 等人[17]利用加同态加密设计实现了加密数据的安全贝叶斯运算. 然而他们的方案只是部分实现了贝叶斯分类器的构建, 仅仅通过聚合协议实现了从加密数据集中统计类标签的频数. 待分类样本的频数以及先验概率仍然需要在明文上进行计算. Zhu 等人[18]结合Paillier 同态加密和不合谋的云服务器模型设计了加密数据安全贝叶斯模型训练和分类方案, 实现了从加密数据集中训练贝叶斯模型参数并进行分类运算. 但是他们的方案所需的计算和通信开销太高, 无法应用于大规模数据集中. 与本文研究内容相关的另一些文献[19,20] 运用差分隐私来实现隐私保护朴素贝叶斯训练和分类. 文献[19] 提出的方案中需要一个可信第三方称为数据收集者收集用户数据, 向其中添加特定的扰动, 从而在实现差分隐私的同时计算朴素贝叶斯分类. 为了避免使用可信第三方, 文献[20] 设计了本地差分隐私下的联合分布估计机制并基于此提出了本地差分隐私下的朴素贝叶斯训练和分类方案. 这一方案虽然保护了数据集的隐私, 但是将训练好的朴素贝叶斯模型泄漏给了第三方. 本文结合SHE 加密算法、SIMD 技术和混淆电路提出了加密数据安全朴素贝叶斯训练和分类方案,使得云服务器能够在外包加密数据集上安全批量训练出朴素贝叶斯模型参数, 并对待分类样本进行分类运算. 本文提出的方案保护了外包训练数据集、待分类样本、朴素贝叶斯分类器以及分类结果的隐私信息,并且能够高效地在大规模加密数据集上进行运算. 本文在半诚实模型下证明了提出方案的安全性并通过实验对其性能进行了评估. 实验结果表明提出方案相比现有工作具有更好的运行效率.3 问题描述和运算原语
3.1 系统模型
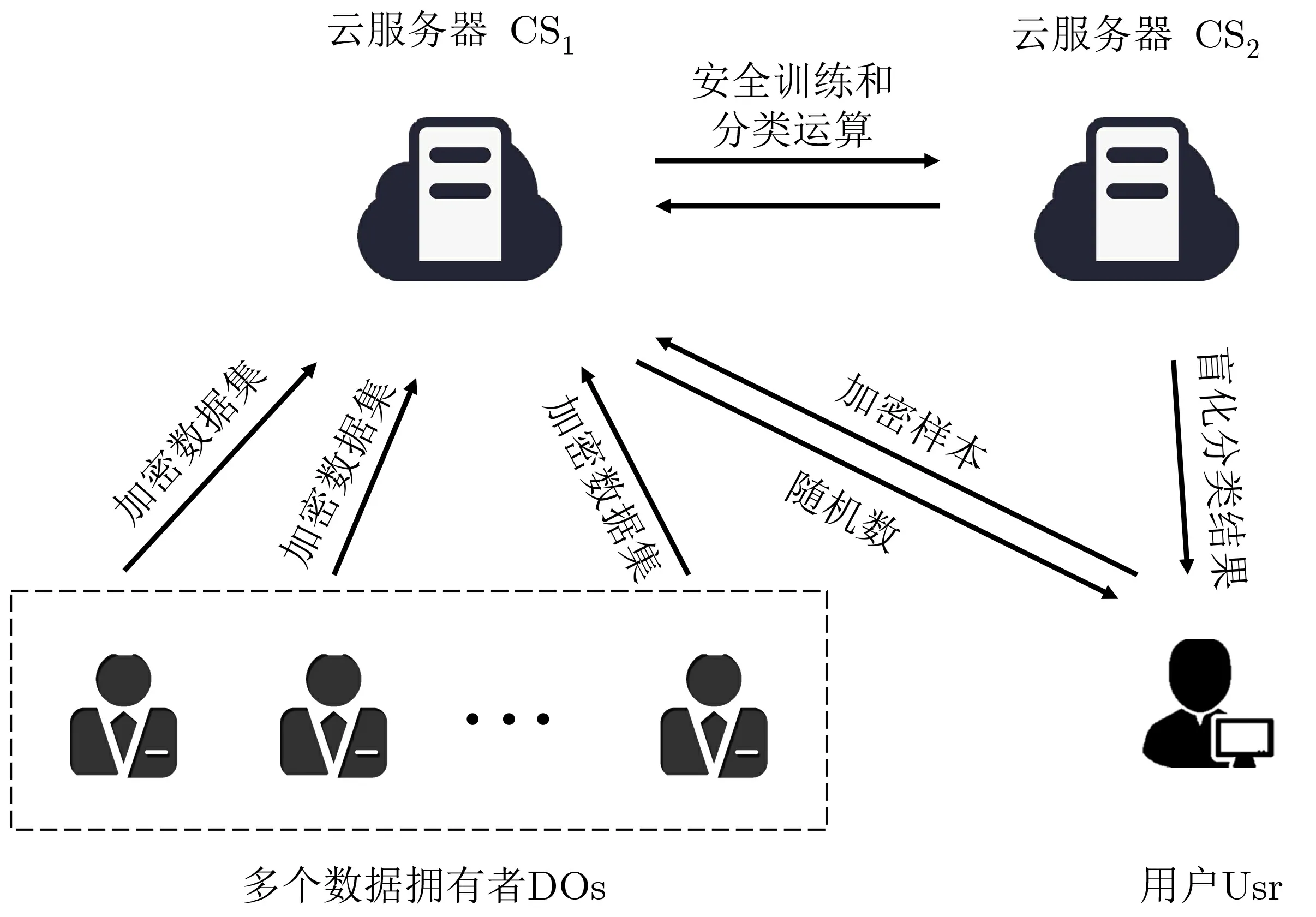
3.2 安全模型
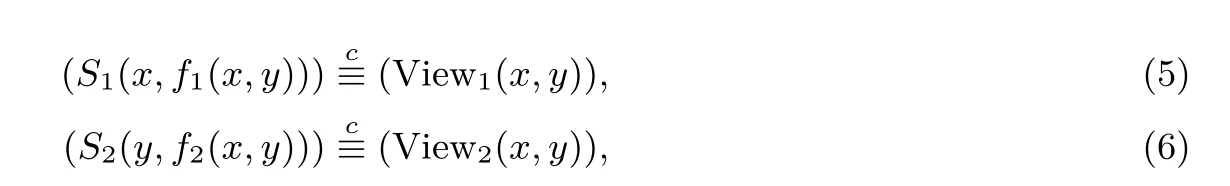
3.3 明文数据编码

3.4 安全运算原语



4 安全朴素贝叶斯训练和分类方案

4.1 初始化
4.2 数据集加密

4.3 安全类标签频数计算

4.4 安全待分类样本频数统计




4.5 安全类标签判断



5 方案分析
5.1 安全性分析






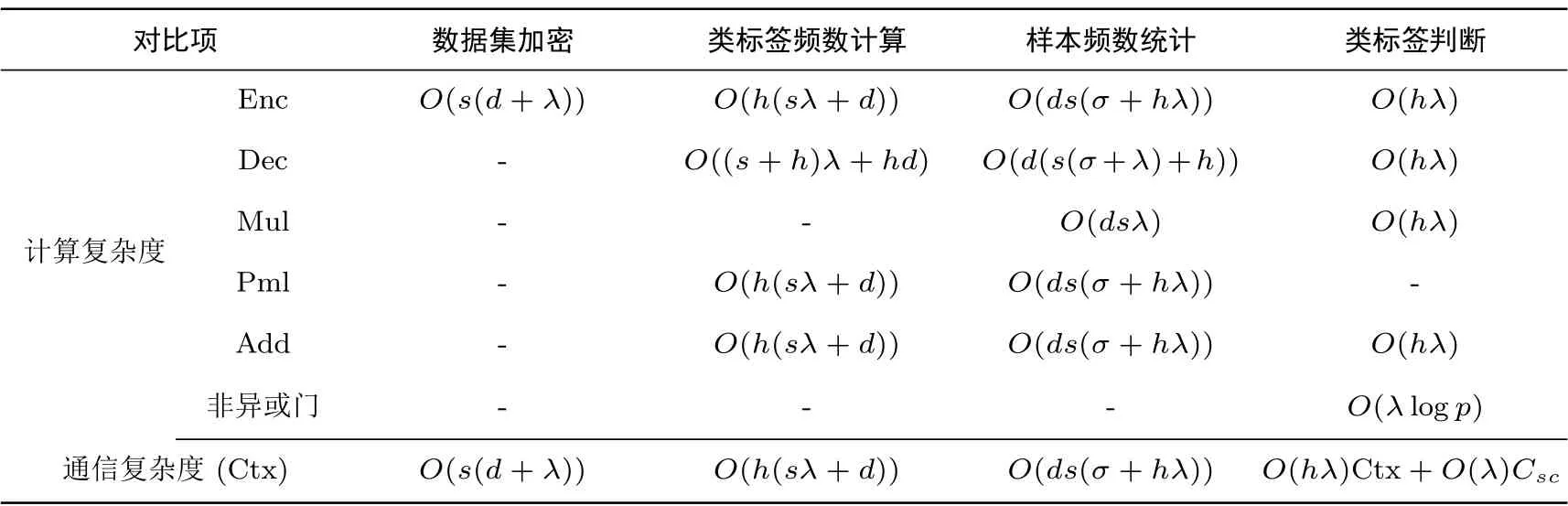
5.2 复杂性分析


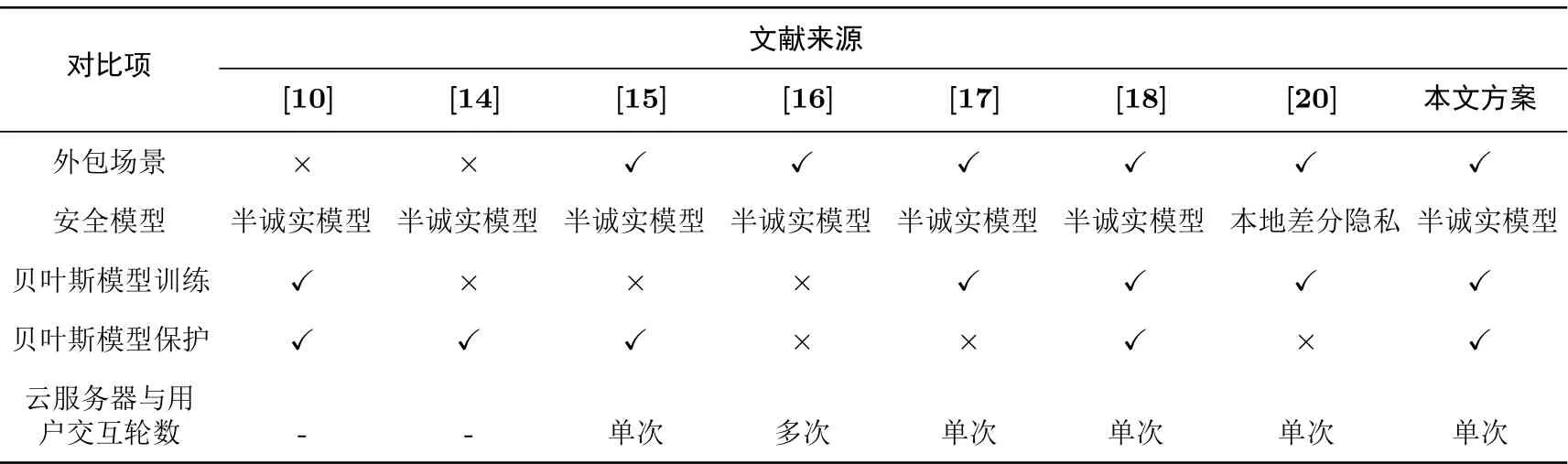
5.3 对比分析
6 实验评估

6.1 方案性能评估
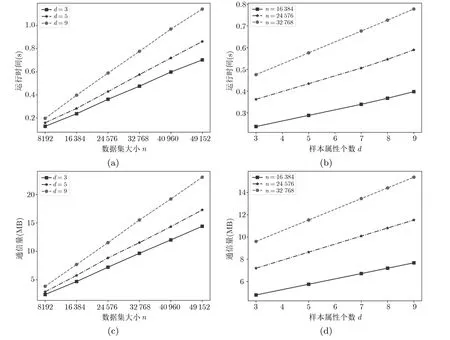
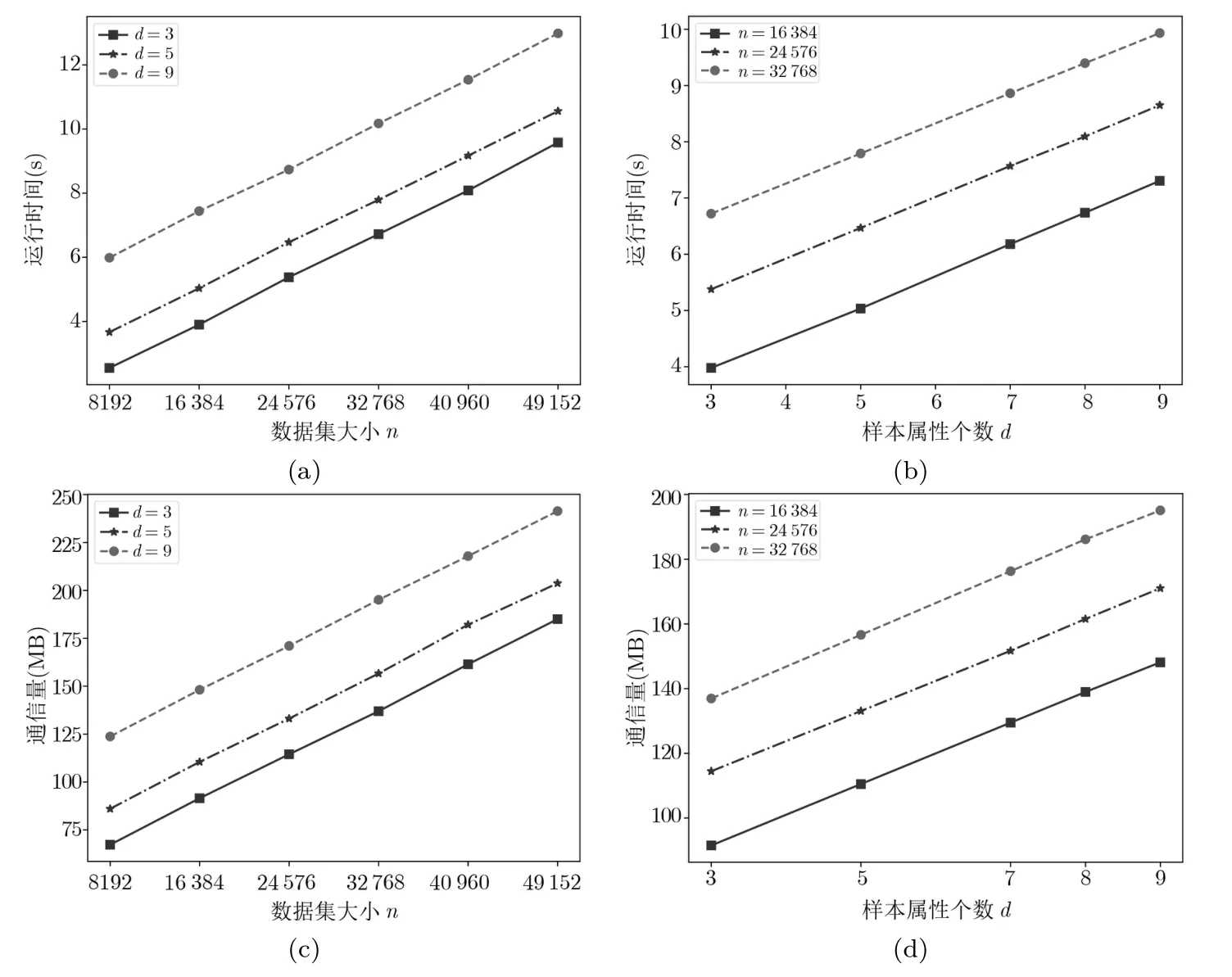
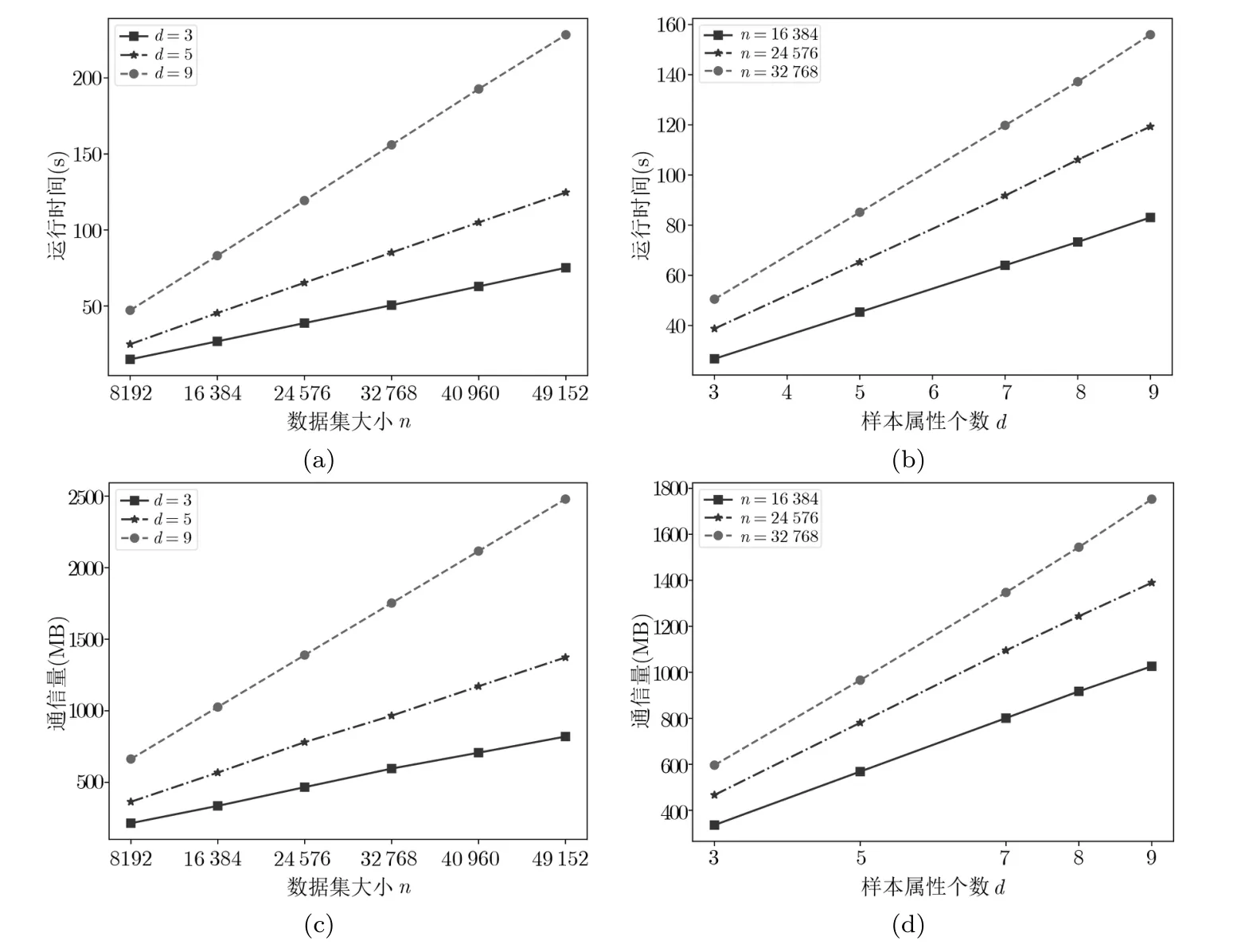

6.2 与现有工作对比

7 相关工作
8 总结
