区块链多链下的数据隐私保护K均值聚类算法*
2022-07-12徐志锟肖梦雪
左 力,徐志锟,肖梦雪
(西南交通大学,四川 成都 610031)
0 引言
区块链是一种多方参与维护的块—链式数据结构,利用分布式节点共识算法生成和更新数据,并利用密码学的方式保证数据传输和访问的安全,具有去中心化、高透明度、不可篡改、可编程、可追溯等特点[1]。
开源区块链平台以太坊(ethereum)的诞生促使该平台上落地了大量的去中心化应用(Decentralized Application,DApp),自此,区块链技术在越来越多的行业中得到了应用[2]。不局限于金融领域和加密数字货币领域,近年来人们开始尝试将区块链应用于政务、医疗、教育、服务、物流等众多领域。
这些不同领域中的每条应用链相互独立地运行和存在。为了更好地利用这些区块链当中的数据,人们希望对其进行更深层次的分析。利用数据挖掘技术可从这些区块数据中提取有价值的信息,因此多链之间必定会发生跨链交互行为。但在区块链多链的应用场景下,对数据进行挖掘分析需要通过多区块链应用方之间的配合来完成。传统的集中式数据挖掘无法完成该任务,这是因为首先区块链系统具有去中心化的结构特点,无法将存储在各条链上的数据存储到一个中心进行挖掘;其次在多链之间配合进行数据挖掘时,考虑到某些区块链上可能含有具有商业价值的信息或者较敏感的隐私数据,如医学研究领域和市场动态研究领域的区块链,数据拥有者通常希望能够在不与他人共享这部分私有数据的同时获得数据的分析结果[3]。因此在多链环境下提出能保持数据隐私性的挖掘算法具有重要意义,使得挖掘者只能获得正确的挖掘结果,而不会获得其他任何信息。
本文结合聚类挖掘方法中的K均值聚类来对多条区块链当中的数据进行分析。K均值是经典的基于距离划分的聚类算法,其具有简单高效的特点,在很多领域都得到了广泛应用[4]。综上,为了解决多链合作进行聚类挖掘时带来的隐私泄露和敏感信息被发现的问题,本文提出了多链下基于同态加密技术的数据隐私保护K均值聚类算法。
1 同态加密算法
20世纪70年代,Rivest等人[5]首次提出了利用同态加密(Homomorphic Encryption,HE)技术来保护数据的安全性。同态加密是一种利用具有同态性质的加密函数,允许直接对密文进行操作,并保护数据安全性的加密变换技术[6]。这一特性使得同态加密技术具有保护数据安全性的特点。利用该技术可以使得区块链数据挖掘方只能获知最后的挖掘结果,而无法从获得的结果中分析得到其他被挖掘者的任何信息,既满足了用户可以对敏感数据进行操作的需求,又避免了数据信息泄露的风险,提高了信息的安全性。
此外,利用同态加密技术可以使得数据挖掘者即使在不知晓密钥的情况下,仍然可以对密文进行计算,这在一定程度上可以减少通信代价,并平衡各参与方的计算代价。正是因为同态加密技术在降低通信复杂度和计算复杂度以及保护数据安全性上具有优势,越来越多的研究者投入到其理论和应用的探索中[7]。
1.1 算法主要步骤
为保障密钥的安全性,密钥选取应当满足以下基本特性:
(1)对于任何参与者来说,给定的某个明文信息m∈Zr={0,1,2,3,…,r-1}想要形成加密后的密文z∈Er(m)时,在计算上都应该是容易的;
(2)对密文z∈Er(m)进行解密后的结果应当是唯一的,即如果m1,m2∈Zr,且满足m1不等于m2,则Er(m1)与Er(m2)的交集应当为空集,并且拥有私钥的一方应当能够计算出这个唯一的解;
(3)在适当的密码学假设下,仅仅通过加密算法Er和密文z∈Er(m),想要得到明文m或者私钥在计算上是不可行的。
具体的同态加密密钥生成算法步骤如下文所述。
(1)选择两个大素数p和q,并计算两数的乘积n=p×q。
(2)选择一个实数r,使r满足r可以整除(p-1),r与(p-1)/r互素,r与(q-1)互素这3个条件,如图1所示为实数r的选择流程。

图1 满足条件的实数r找寻流程
(3)选择底数y,该底数y的取值范围应为y∈(Zn)*={x∈Zn:gcd(x,n)=1},并且y需要满足不等式:

由此3个步骤可以得到一对公钥PK=(y,r,n)与私钥SK=(p,q)。
明文m必须是集合Zr上的元素,实数u为加密时在集合(Zn)*上产生的随机数,对明文m的加密算法为:
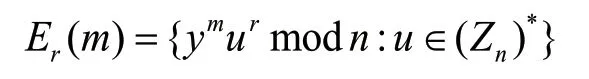
对于任意的明文m和随机数u,则有:

因为m 同态特性使得同态加密技术具有保护数据安全性的特点,因此需要对其同态特性进行证明。根据加密算法对明文m1和明文m2进行加密: 将密文相乘,得到: 通过该等式可以证明得到: 基于这个特性,该同态加密方案可以使得两个密文的乘积在经过解密后得到的结果与对应明文相加后的结果相等。 同态加密在多链下的隐私保护数据挖掘当中,主要用来解决加权平均问题(Weighted Average Problem,WAP),该问题定义为,已知(x,n)和(y,m)的两方Alice和Bob都想要得到双方数据共同的加权平均值(x+y)/(n+m),而双方都不想让对方知晓自己所掌握的私密数据。 利用同态加密技术解决WAP问题的步骤如下文所述。 (1)Alice按照同态加密算法的密钥生成方法生成一对公钥与私钥,并公布自己的公钥给Bob。 (2)Alice使用自己的公钥通过加密算法加密自己的私有数据(x,n),将加密结果E(x)和E(n)发送给Bob。 (3)Bob得到Alice发来的加密消息E(x)和E(n)后,任意产生一个随机数z,根据同态加密的特性,Bob可以通过求幂运算计算得到两个值(E(x))z=E(z×x)和(E(n))z=E(z×n),并且Bob还可以使用Alice的公钥加密自己拥有的加入随机参数后的私有数据(z×y,z×m),得到加密结果E(z×y)和E(z×m)。在得到4个加密数据后,Bob再次利用同态加密的性质向Alice发送两条加密消息E(z×x+z×y)=E(z×x)×E(z×y)和E(z×n+z×m)=E(z×n)×E(z×m)。 (4)Alice收到Bob发送来的加密数据E(z×x+z×y)和E(z×n+z×m)后,可以利用自己的私钥对其进行解密,得到明文z×x+z×y和z×n+z×m,通过求商约分计算,Alice得到加权平均值(x+y)/(n+m)。 (5)Alice将计算得到的结果发送给Bob。 同态加密解决WAP问题的过程如图2所示。 图2 同态加密解决WAP问题的过程 通过同态加密技术解决了加权平均值求取的问题,同理可以将其推广到多方区块链应用中,用于解决分布式条件下的数据挖掘问题。 i条链下隐私保护求取加权平均值需要除数据挖掘方以外的(i-1)条链都产生自己私有的随机数z1,z2,…,zi-1,然后利用数据挖掘方的公钥和同态加密的性质,在(i-1)条链之间传送加入了自己私有随机数的明文加密后的密文,最后将加入了所有随机数的密文数据E(x1×z1z2…zi-1),…,E(xi×z1z2…zi-1)和E(n1×z1z2…zi-1),…,E(ni×z1z2…zi-1)传送给数据挖掘方,利用自己的私钥和同态加密的性质,挖掘方便可以获得加权平均值。 聚类是指按照某个特定标准将物理或抽象对象的集合分割成不同的类或簇的过程[8]。聚类应使得同一个簇内的数据对象的相似性尽可能大,同时不在同一个簇中的数据对象的差异性也尽可能大[9]。相似性与差异性是根据数据对象的属性值进行评估的,通常可以采用距离进行度量[10]。聚类分析就是从给定的数据集中搜索数据对象之间所存在的有价值联系[11]。 本文结合K-means聚类算法对多链数据进行挖掘,其核心是一种迭代求解的聚类分析算法。随机选取k个对象作为初始的聚类中心,然后计算每个数据对象与各个种子聚类中心之间的距离,把每个对象分配给距离它最近的聚类中心[12]。每分配一个数据对象,聚类中心就会根据当前聚类中的所有对象重新计算获得一个新的聚类中心。不断重复这个过程直到满足终止条件时,完成聚类。 假设有i条链的数据需要在不泄露隐私的情况下进行K-means聚类分析,第1条链拥有a个数据(X11,X12,…,X1a),第2条链拥有b个数据(Y11,Y12,…,Y1a),第i条链拥有c个数据(Zi1,Zi2,…,Z1c),任何一方都需要在不知晓其余参与方具体数据的情况下获得共同K-means聚类结果。具体的算法流程如图3所示。 图3 分布式K-means聚类流程 假设以第1条链为主分析该算法,第1条链拥有a个数据(X11,X12,…,X1a)。由第1条链产生m个初始聚类中心(U1,U2,…,Um),产生的方式可以是随机的,也可以通过各种提取初始聚类均值的技术来选取。将初始化的m个聚类中心发送给其余(i-1)条链,各链根据初始化的聚类中心来计算自己拥有的每一个样本数据到聚类中心的距离,该距离可以用各种度量方式选择,如欧式度量、分散度量等,若某样本离某聚类中心的距离最近,则将此样本归类为这个簇中。 依据此方式,将第1条链的样本数据分别进行聚类,并且通过计算可以得到新的聚类中心(U11,U12,…,U1m)和每一个聚类簇中的样本数量(N11,N12,…,N1m),记每一个聚类簇中的数据和为P1j,j∈[1,m],其中,Pj=∑Xj=Uj×Nj,记每一个聚类簇中的样本数量为Q1j,j∈[1,m],其中,Qj=Nj。同样地,其余(i-1)条链也可以得到新的聚类中心(U21,U22,…,U2m),…,(Ui1,Ui2,…,Uim)和每一个聚类簇中的样本数量(N21,N22,…,N2m),…,(Ni1,Ni2,…,Nim),记每一个聚类簇中的数据和为P2j,…,Pij,j∈[1,m],记每一个聚类簇中的样本数量为Q2j,…,Qij,j∈[1,m]。 此时,i条链都拥有各自的m组数据(Pkj,Qkj),k∈[1,i],j∈[1,m],通过基于同态加密的隐私保护协议,每一条链可以在不知道其余链任何数据的情况下得到共同的聚类中心(U1,U2,…,Um),即解决隐私保护下的加权平均求值问题。 双方在计算得到新的聚类中心之后,再次按照上面的步骤进行聚类,重复整个过程,每次迭代都会重新分类样本并计算均值,当检测到均值没有变化的时候,算法终止。“没有变化”的精确定义取决于所使用的具体指标,可以是没有对象被重新分配给不同的聚类,没有聚类中心再发生变化,误差平方和局部最小等。 通过多链下的隐私保护K-means聚类数据挖掘方法可以在达到想要的数据挖掘目标的同时,保护用户隐私数据不被泄露。该算法可以应用到许多领域当中,并根据该领域的需求作出调整,比如应用于金融领域中解决金融系统问题时,需要根据多个应用上的历史交易记录来判定用户是否可信任,并保证用户数据不泄露;再比如应用于推广领域中时,需要在不泄露用户信息的情况下分析客户的需求,以便向其推广相应的目标产品[13]。 由于各链进行聚类划分和计算聚类中心的过程都是在本地完成的,因此多链联合计算过程中的安全性问题主要集中在各链将自己加密后的数据发送给其他链后,其他链是否有能力从中获得与原始数据有关的信息。 因为各链发送的数据都通过加密,而且其中还受不确定的随机数的影响,而利用同态加密的性质,即使是在对其他链的数据进行计算时也不需要对数据进行解密,而是直接对密文进行运算操作,这样保证了在多链联合计算时各链的私有信息不被泄露,并且整个计算过程的加密和解密操作全由各链独立完成,所以可以保证在多链联合计算过程中各链数据的安全性。 多链联合计算的通信过程主要是在计算加权平均值问题时需要传送信息,在这整个通信过程中没有出现明文,都是利用同态加密的特性直接对密文进行操作完成运算。当存在窃听行为时,假设多链在求解加权平均值的过程中被窃听到了密文数据,但由于其没有私钥,破解密文的难题便归结到了大数分解和素性检测上,这无疑是困难的。即便是拥有私钥的一方与窃听者合谋共同破解原始数据,但由于加密的明文当中含有其余方产生的随机数,因此,窃听者无法还原出原始数据,从而保证了多链下联合计算的通信过程中的数据安全性。 多链下的数据隐私保护K均值聚类算法只是将K均值聚类放到了多链分布式环境下,并在过程中加入了数据隐私保护技术,并没有改变原来的K均值聚类的迭代过程。原始的K均值聚类算法结果的差异性在于初始聚类中心的选取方式和距离的计算方式上[14]。本文提出的K均值聚类算法并没有改变两者,因此仍然可以将其他能够提高聚类精度的方法嵌入到该算法当中,且迭代过程中依然是从第1次迭代到最终次迭代不断修正聚类中心,所以算法的正确性可以得到保证。 本文针对区块链环境下时常既需要进行多链联合计算分析多链数据中的一些有用信息,又要确保不能泄露任何隐私信息的痛点,提出了一种多链下保护数据隐私的K均值聚类挖掘算法。该算法基于同态加密技术,在计算和通信过程中都可以在加密的环境下进行,而不需要对其进行解密,从而达到不泄露任何私密数据的目的。1.2 同态性质证明

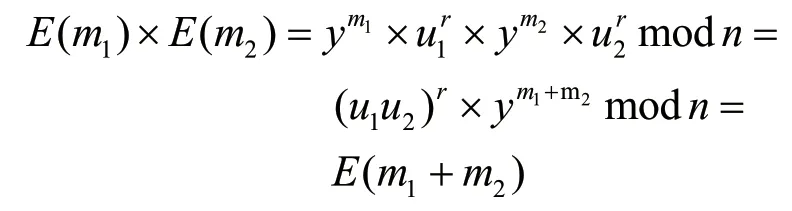

1.3 数据挖掘中的应用

2 多链下的数据隐私保护K均值聚类算法
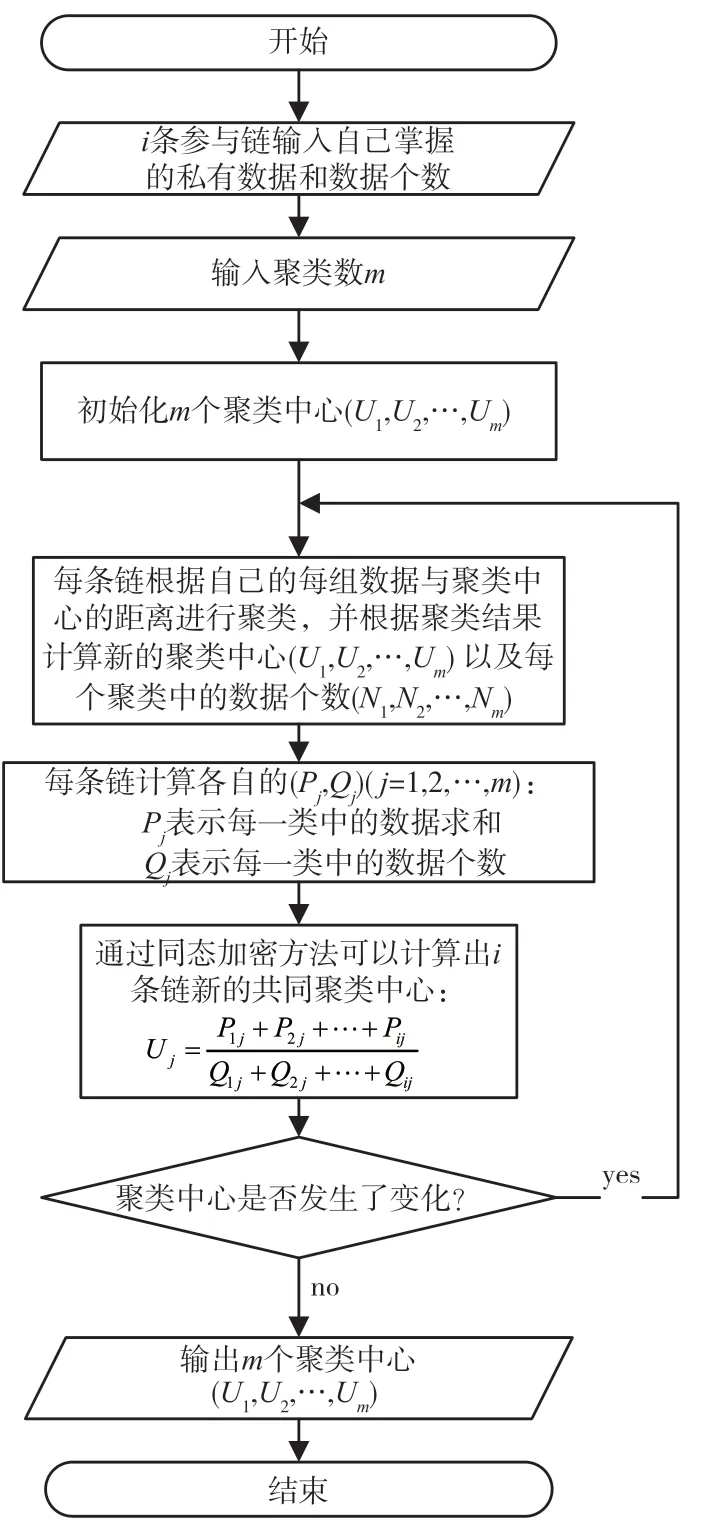
3 算法分析
3.1 计算过程中各链数据的安全性
3.2 通信过程的安全以及防窃听性
3.3 聚类精度分析
4 结语
