基于量子进化的天牛须搜索算法*

刘亚奇

（河南工业大学，河南 郑州 450001）

0 引言

群智能算法是模拟生物群体行为规律的算法，用来解决复杂的优化问题，如蚁群算法[1]、粒子群优化算法[2]、麻雀搜索算法[3]等。2017年，Jiang和Li受到天牛觅食和寻偶过程的启发，提出了天牛须搜索（Beetle Antennae Search，BAS）算法[4]。该算法不需要函数的梯度信息就能实现优化，因此复杂度低，其核心代码仅有4行。BAS算法一经提出就受到了广泛关注，同时对BAS算法的改进也是很热门的研究方向。Lin等人[5]把BAS算法和粒子群优化（Partical Swarm Optimization，PSO）算法结合起来，前期用PSO算法更新粒子的速度和位置，后期用BAS算法进行局部的搜索优化，取得了比单纯采用BAS算法或PSO算法更好的优化效果。邵良杉等人[6]提出了一种基于BAS的花朵授粉算法，记为BASFPA。此算法在全局搜索的时候用BAS算法加快收敛速度，在局部搜索的时候引入变异策略，加快了收敛速度，提高了搜索的成功率。廖列法等人[7]提出了一种基于二次插值的BAS算法QIBAS，在天牛搜索的过程中引入二次插值更新BAS算法的最优适应度值，避免陷入局部最优。

本文在总结以上改进方法的基础上，提出了一种基于量子进化策略的BAS算法（QBAS），把当前最优解认为是“正”“伪”两种状态概率的线性叠加，用实数编码的量子（RCQ）表示当前最优解，然后用量子旋转门（Quantum Rotation Gate，QRG）更新当前最优解的概率。

1 BAS算法

1.1 数学模型

BAS算法的数学模型如下文所述。在D维空间中，天牛左右须xl和xr的位置表示为：

式中：xt为天牛在t次迭代时的位置；dt为天牛两须之间的距离；b为天牛的随机朝向。b的计算方式为：

式中：rands(·)为随机函数。

根据两侧触须的气味浓度，更新天牛的位置：

式中：δt为步长因子；f(·)为适应度函数；sgn(x)为符号函数。

更新下一步的搜索范围和步长：

式中：eta为两须距离和步长的衰减系数，通常取0.95。

1.2 算法流程

BAS算法的具体运算过程如下文所述。

步骤1：设置控制参数，初始化天牛的位置信息xt(t=0,1,2,…,n)。

步骤2：计算天牛适应度函数值fitness(xt)并存储当前最优解xbest和fitness(xbest)。

步骤3：随机生成步长b，根据式（2）进行归一化处理。

步骤4：根据式（1）计算天牛的左须xl与右须xr位置。

步骤5：根据式（3）更新天牛的位置xt+1(t=0,1,2,…,n)。

步骤6：根据式（4）和式（5），更新搜索范围δ和步长d；

步骤7：判断是否满足迭代终止条件，若是则跳转到步骤8，否则跳转至步骤2。

步骤8：输出全局最优解xbest和fitness(xbest)，结束。

2 基于量子的天牛须搜索算法

1996年，Narayanan等人[8]将量子理论与进化算法相结合，提出了量子遗传算法（Quantum-Inspired Genetic Algorithm，QIGA）。2004年，Han等人[9]在此基础上将此算法扩展为量子进化算法（Quantum Evolutionary Algorithms，QEA），用 量子位编码表示染色体（RCQ），在算法后期用QRG完成更新。Chen等人[10]设计了一种基于量子进化的鸽群算法，经过实验验证其具有优越的寻优性能。

2.1 RCQ操作

量子进化算法是基于量子比特和量子力学态叠加的概念，其中量子比特又称为量子位，是指存储在量子计算机中的最小的信息单位。量子位可以用正态与伪态表示，具体表现为“0”态和“1”态。量子位状态被表示为：

式中：α和β分别为两种状态的线性概率。α和β满足：

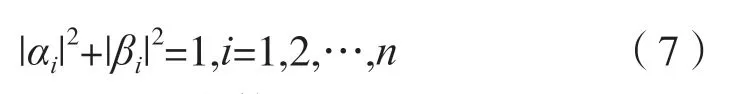
则n个量子位的染色体形式表示为：

式中：n为算法种群；t为迭代次数；qjt为染色体。

当前最优解被认为是“0”态和“1”态的线性叠加，最优解的量子由RCQ表示为：

此时，天牛的收敛方向重新被观测后定义为xbest，表达式为：

在量子力学中，量子态可以用波函数ω(x,t)表示。波函数的平方|ω(x,t)|2称为概率密度，表示量子态在对应时间和位置出现的概率。式（10）表示当前RCQ的观测值，可以用概率密度求得，概率密度的表达式为：

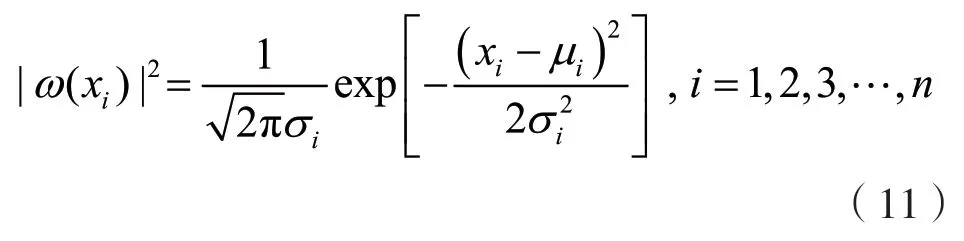
式中：μi为期望值，用当前最优解表示；σi为方差。σi定义为：

式中：σi为量子进入正确方向的概率；|ψi〉由随机得到。

2.2 QRG操作

在量子进化算法中，因为量子位编码下的染色体不是单一状态，不能进行传统的选择、交叉、变异等操作。本文采用QRG[11]作用于量子位上，使其状态位发生变化，进而改变αi的分布域。对于有n个量子位的个体，第i个量子位的更新情况如下：

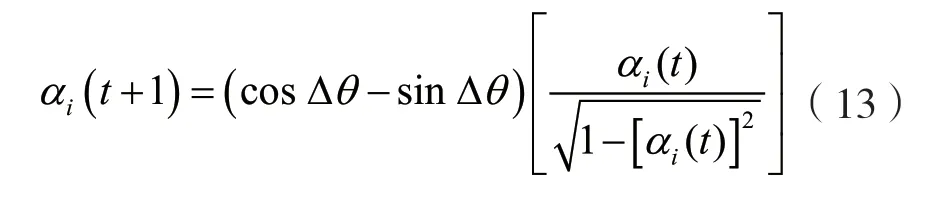
式中：Δθ为旋转角度，是与收敛速度有关的设计参数，等同于定义当前最优解的收敛速度的步长。为了防止量子位被困在0或1，对α施加一个约束，使概率αi2(t)收敛于ε或者1-ε，而不是0或者1。本文中，使用QRG策略是为了让量子位的概率趋近于正确的方向，从而提高了正概率的变异策略。如果迭代后当前最优解没有变化，就通过QRG增加α，意味着更有可能是全局最优解，让算法跳出局部最优解，避免早熟收敛，否则量子位的概率值就被重置为初始值，以保持对算法欺骗性的警惕，其计算方式为：

2.3 QBAS算法流程

步骤1：设置控制参数，初始化天牛的位置信息xt(t=0,1,2,…,n)。

步骤2：计算天牛适应度函数值fitness(xt)并存储当前最优解xbest和fitness(xbest)。

步骤3：根据式（9），对当前最优解用实数编码的量子（RCQ）表示。

步骤4：根据式（10），重新定义天牛的收敛方向xbest,i。

步骤5：随机生成步长b，根据式（2）进行归一化处理。

步骤6：根据式（1）计算天牛的左须xl与右须xr位置。

步骤7：根据式（3）和式（10），由新的收敛方向更新天牛的位置xt+1(t=0,1,2,…,n)。

步骤8：计算更新位置后的适应度值fitness(xt+1)，存储当前最优解

步骤9：根据式（4）和式（5），更新搜索范围δ和步长d。

步骤10：判断是否满足迭代终止条件，若是则执行步骤12，否则跳转至步骤11。

（a）根据式（13），执行量子旋转门（QRG）操作；

（b）根据式（9），对当前最优解用实数编码的量子（RCQ）表示；

迭代至t=t+1，返回步骤4。

3 仿真实验与结果分析

3.1 测试函数介绍

本文在MATLAB 2018a软件上进行仿真测试，用6组标准测试函数进行对比实验，测试函数的名称、表达式以及搜索范围和全局最优解，结果如表1所示。其中，F1、F2和F3是单峰函数，在其定义域上只有一个全局最优解，可以用来测试算法挖掘群体信息的能力和收敛精度的高低；F4、F5和F6是多峰函数，意味着函数拥有多个局部极值，可以很好地测试算法深度搜索种群以外其他信息的能力和解决复杂优化问题的能力。

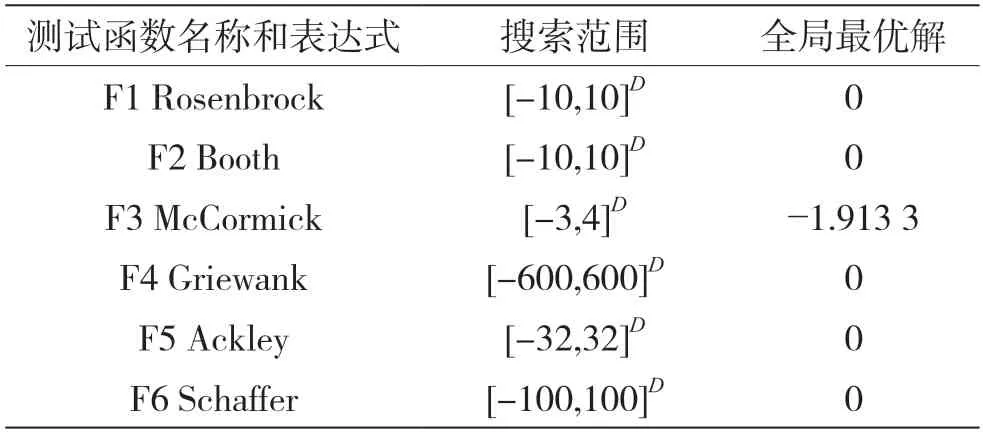
表1 测试函数的名称、搜索范围和全局最优解

本实验中选取3个指标评价算法的性能：（1）最优值是算法输出的适应度值中，趋近函数全局最优解的值，反映了算法的寻优能力；（2）平均值是算法多次迭代结束后输出的适应度值的平均值，反映了算法求解能力的好坏；（3）方差是迭代结束输出的适应度值与均值之间的方差，能够反映算法的稳定性。

3.2 算法优越性检验

本文将QBAS算法与PSO[2]和遗传算法（Genetic Algorithm，GA）做对比测试。把3个算法的参数设置成一样，最大迭代次数为100，种群个数为10，搜索空间维度为30，QBAS算法的步长衰减系数eta为0.95，步长δ为10。PSO算法的学习因子设置为c1=c2=1.5，惯性权重ω为0.8。GA算法的交叉算子CR设置为0.1，变异算子F设置为0.4。对每个测试函数各运行30次，记录输出的适应度值，同样取3个指标列成表格，如表2所示。

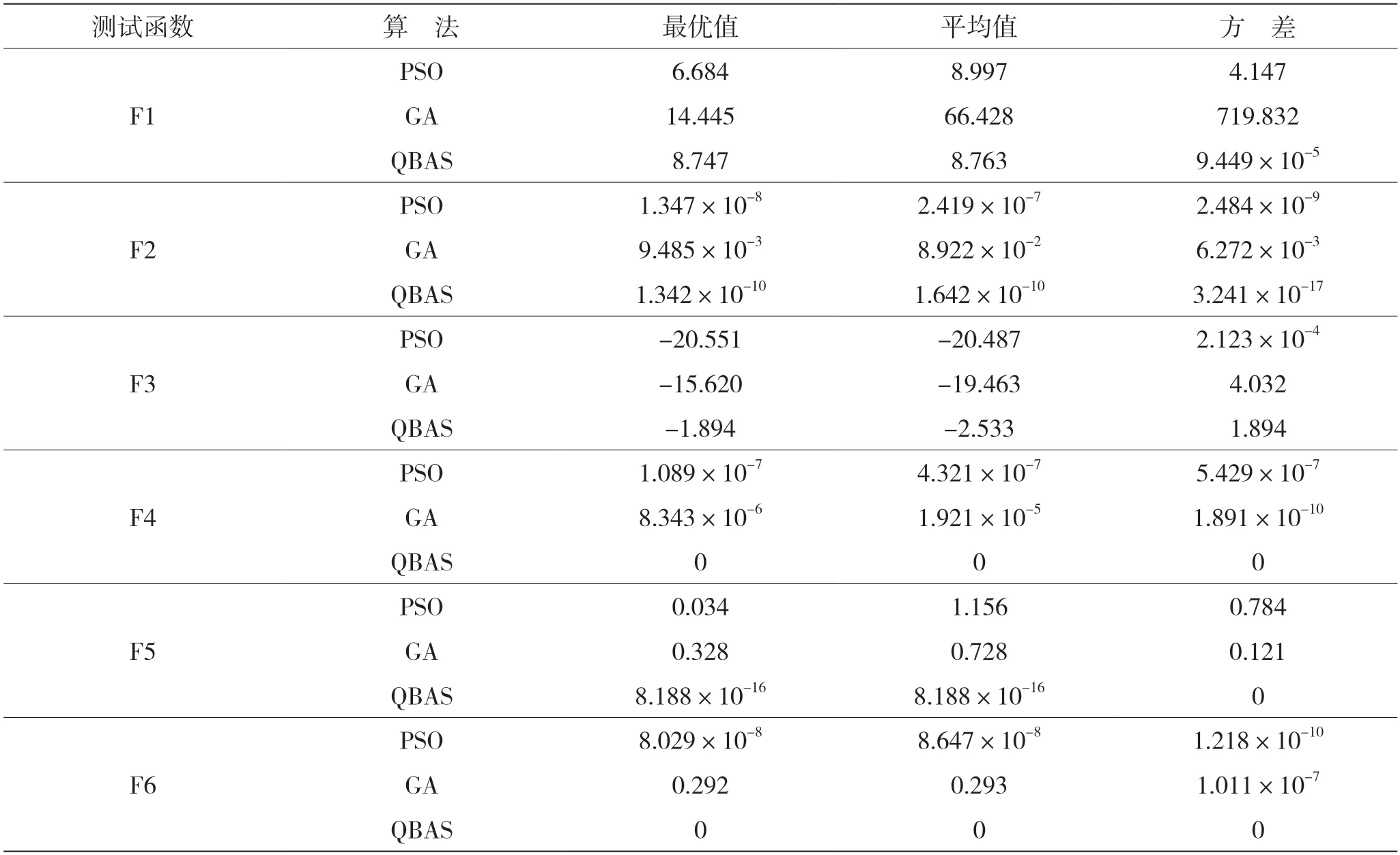
表2 测试函数的最优解、平均值和方差

为了更加直观地比较QBAS与其他两种优化算法的寻优性能，本文将各算法的收敛曲线用电脑软件MATLAB 2018a进行仿真，结果分别如图1、图2、图3、图4、图5和图6所示。

图1 函数F1收敛情况

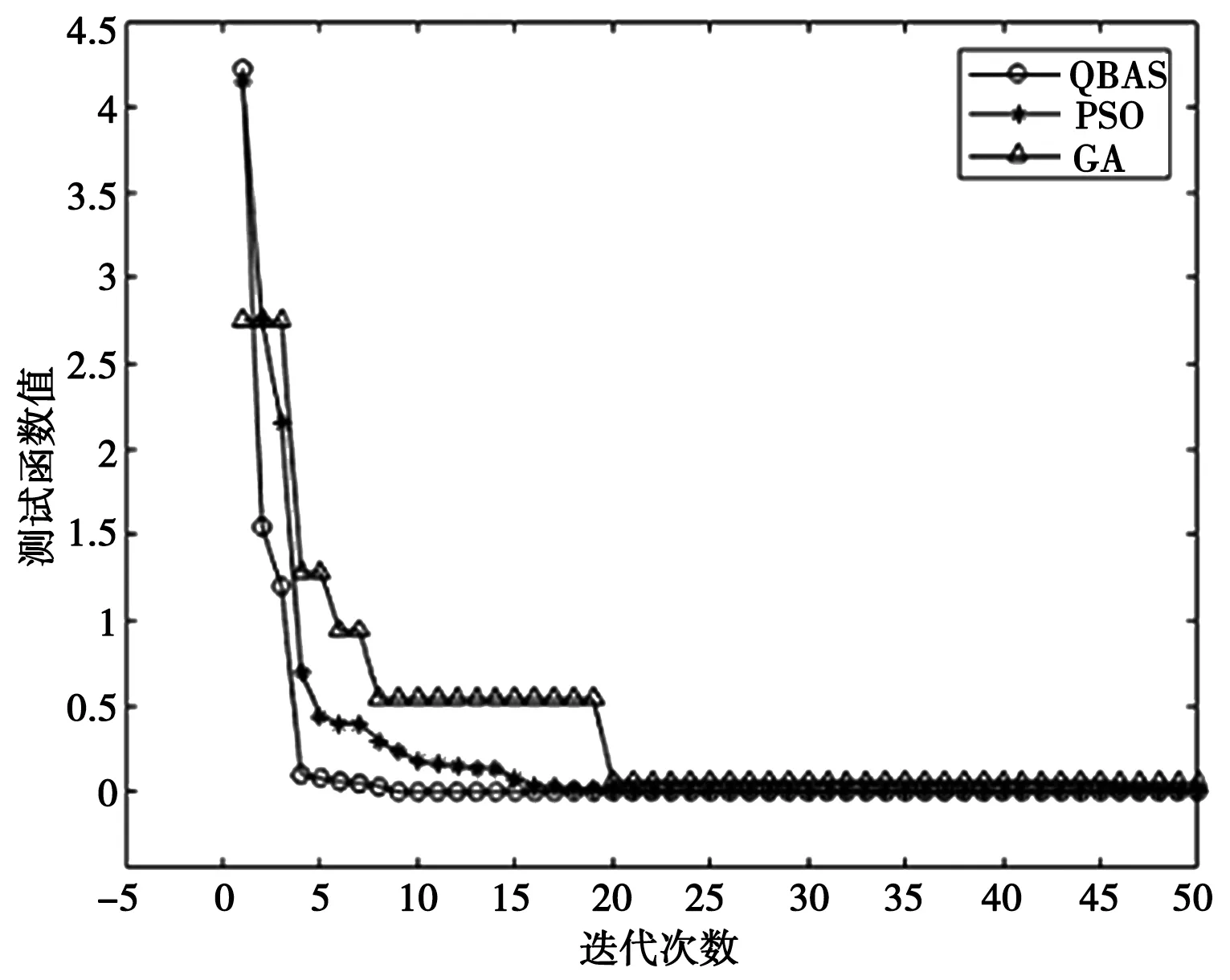
图2 函数F2收敛情况

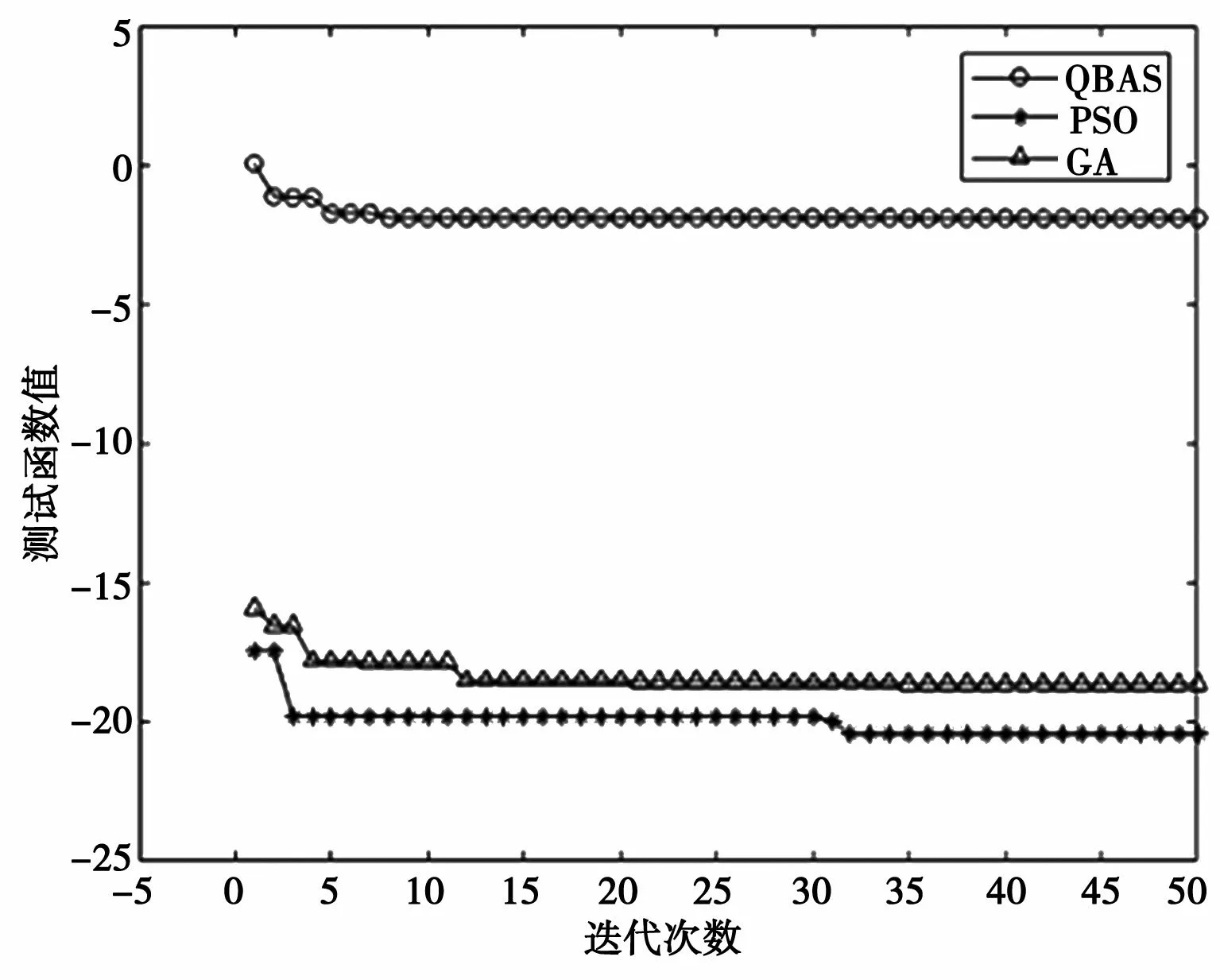
图3 函数F3收敛情况

图4 函数F4收敛情况

图5 函数F5收敛情况

图6 函数F6收敛情况

对F1、F2和F3这3个单峰函数求解可知，除函数F1外，QBAS算法输出的最优值更加趋近于函数的实际全局最优值，尤其是对函数F3的求解中，PSO算法和GA算法从运算的一开始就陷入了局部最优值，并且无法跳出来。对函数F1的求解中，由均值和方差两个指标可知QBAS算法的稳定性更强。由函数F1、F2和F3的收敛图可知，QBAS算法的收敛速度更快，基本不会陷入局部最优，获得最优解的迭代次数也较少，运算速度更快。对F4、F5和F6这3个多峰函数求解可知，QBAS算法输出的最优值均更加趋近于函数的实际全局最优值，尤其求解函数F4和F6的输出适应度值均等于函数实际全局最优值。由此可见相比单峰函数，QBAS算法对多峰函数的寻优性能更加优越。

4 结语

本文在天牛须算法中引入量子进化算法的实数编码的量子（RCQ）和量子旋转门（QRG）策略。实验结果表明，对于9个标准测试函数，基于量子进化的天牛须搜索算法（QBAS）具有更优越的寻优性能，能利用较小的种群和较快的迭代速度获取最优值。