复杂地形条件下多AIRS辅助角度域AoA定位方法*

于 莹，许 魁，夏晓晨，周 涛，李博扬，李海泉

（中国人民解放军陆军工程大学，江苏 南京 210007）

0 引言

随着5G技术在全球范围内广泛应用，对6G的研究随即展开。智能反射面作为未来无线通信的关键技术之一，是近几年的新热点。智能反射面（Intelligent Reflecting Surface，IRS）本质上是一种超材料，利用集成在平面上的大量无源反射阵元，通过硬件或软件编程对入射信号的反射相位和幅度进行控制，实现基于传播环境的智能、可重构无线传输，从而达到提高无线通信系统性能的目的。与传统中继对比，IRS具有增强网络覆盖范围，提高频谱效率、能量效率以及低部署成本的优势[1]。我国幅员辽阔，山川密林、高山峡谷构成了复杂的地形环境，同时城市高楼林立，极其容易造成通信链路的遮挡。IRS便于部署，对工作环境要求不高。使用IRS中继，终端目标点的信噪比与IRS元素的数目平方成正比，可以大幅度地提高终端目标点信噪比。同时，IRS可以方便地布置在建筑物上或借助无人机等部署在空中，利用其良好的反射特性，可以解决高频段通信方向性较差、覆盖不足的问题[2]。6G是万物互通互联的时代，在这个大背景下，IRS将以其部署灵活，支持不同的网络架构和数据应用多样的特点，提升通信质量[3,4]。

IRS在态势感知方面的应用正成为一项研究热点。在任何实际应用场景中，位置信息的重要性都不可忽视。精准获取位置信息不仅可以在系统设计中实现简化波束成形设计，而且可优化IRS的部署，从而更好地服务于整个系统。但目前业界对于IRS的研究很少，并且IRS本身没有感知模块，将其用于定位面临一定的挑战。在文献[5]中，作者初步提出了利用IRS进行无线电定位和映射的可行性以及所面临的挑战。文献[6]研究了IRS辅助的下行用户定位和自适应波束成形策略。文献[7]中提出了一种角度域三维到达角（AoA）定位策略以获取目标点的位置。但在复杂地形条件下，由于目标点的位置未知，AIRS部署位置可能不能够提供强的视距（Line-of-Sight，LoS）条件以进行目标点测向，因此定位误差将会增大。依据目前研究，虽然称IRS为智能反射面，通过一些算法可以实现反射相位、反射幅度可调，但是远远没有达到真正的智能化，同时由于实际场景中目标点多是动态的，为了更好地满足信道条件达到定位目的，实际应用中通常要部署多个IRS。因此，如何在多个IRS中准确选择有效IRS实现精准定位是亟待解决的问题之一。

基于以上分析，本文提出基于离散傅里叶变换（Discrete Fourier Transformation，DFT）的多AIRS级联信道择优算法，主要成果总结如下：

（1）适用场景多样化，可提高定位系统的鲁棒性，对山地、丛林等复杂环境的适应能力较传统定位系统有所增强；

（2）提出的算法复杂度不高，对设备要求低；

（3）仿真结果表明，提出的改进算法能够实现更高精度的目标定位。

1 系统模型

依据实际场景下的定位需求抽象为如图1所示的系统模型，利用升空平台、无人机等设备部署I个空域IRS（Aerial IRS，AIRS）、一个多天线的信号接收基站AP和处于未知位置的目标点，由于山川密林的阻挡，AP与目标点之间不存在视距信道。

图1 系统模型

1.1 信道模型

设AP端竖直配置均匀的天线数量为M的天线阵，每个AIRS载有N个反射阵元，即水平方向上有Nx个反射阵元，竖直方向上有Ny个反射阵元，构成均匀平面阵列（Uniform Planar Array，UPA）结构，且AP的天线间距和AIRS各元素的间距均为d。第i个AIRS到AP的信道可以表示为ci=CM×N，假设信道ci有l条路径，l=1表示LoS路径，l≥2表示非视距（None-Line-of-Sight，NLoS）路径，则有：

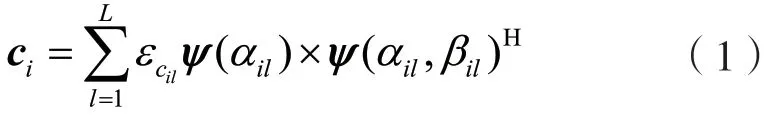
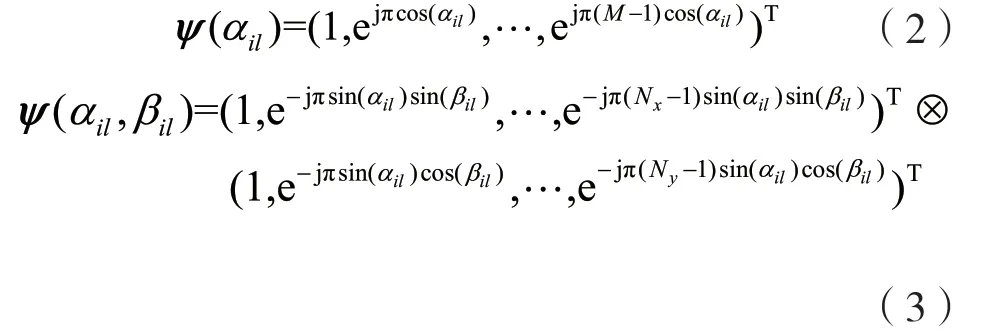
同理，目标点g到第i个AIRS的信道为rgi∈CN×1，假设信道rgi有k条路径，k=1表示LoS路径，k≥2表示非视距（NLoS）路径，则有：

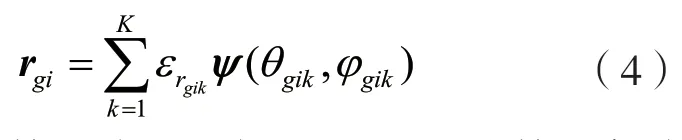
1.2 模型简化

在地对空通信中，无线信道往往是以LoS为主导的，NLoS成分通常可忽略不计[8,9]。实际上，完全的LoS信道适用于建筑物较少的地区或者升空平台的高度足够高（大于40 m）的情况，对于其他环境而言，用概率LoS和莱斯信道模型来表征信道会更加准确[10]。因此本文使用莱斯信道模型来表征信道。根据文献[11]、文献[12]、文献[13]、文献[14]、文献[15]，信道ci和rgi可以简化为：

2 基于DFT的多AIRS级联信道择优算法

2.1 基于DFT的角度域测向算法

文献[7]中研究了AIRS辅助角度域测向算法，其基本原理如下文所述。

AIRS的反射系数矩阵可以表示为：

式中：ain(n=1,2,…,N)为AIRS的振幅反射系数；ejωin表示AIRS处的相移反射系数；ωin∈[0,2π)为AIRS的反射相位。现有研究中，一般不考虑AIRS的振幅反射系数，因此本文只考虑其相移反射系数，为简化计算不妨令ain=1。

由于AIRS为URA结构，可以分辨三维空间的AoA，为便于研究信道fk,i的角度域性质，分析AIRS的反射系数向量为：

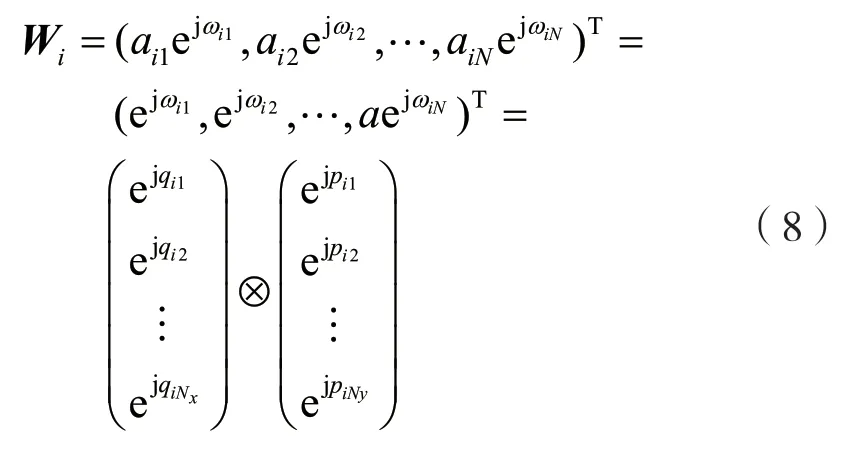
式中：qi和pi分别为水平方向和竖直方向反射阵元的反射相位；⊗为克罗内克积。

基于上述分析，目标g经过第i个AIRS的反射到达AP的信道可表示为：

式中：γ=γciγrgi为常数，表示整个路径的损耗；τ=d/λ，λ为信号波长，ξgn为：

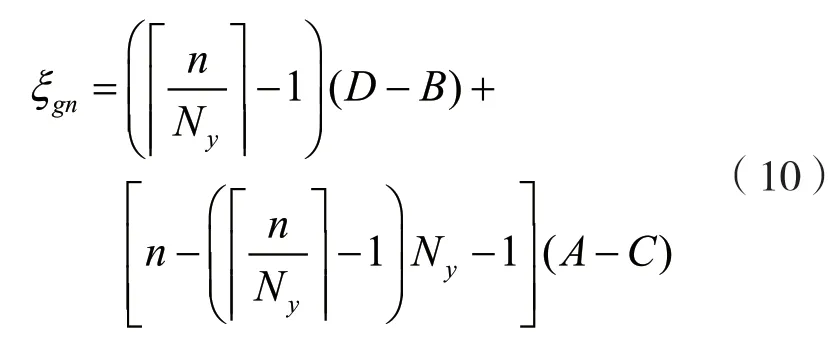
式中：A=sin(αi)sin(βi)；B=sin(θgi)cos(φgi)；C=sin(θgi)sin(φgi)；D=sin(αi)cos(βi)。

为获取路径的角度域信道，对信道Cgi做DFT变换，这里定义M-点的归一化DFT矩阵为：

则Cgi的M-点DFT变换，即Cgi的角度域信道可以表示为：

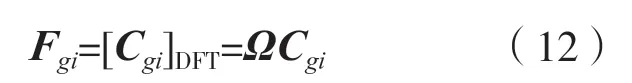
Fgi中第t个元素可以表示为[Fgi]t，将[Fgi]t取模值为：

根据DFT的性质，Ω的每一列表示波束的物理指向，|[Fgi]t|表示各个方向上的增益分布。所有波束都具有正交性，从而形成了正交的波束空间，其中只有少量波束的增益是显著的，指向了信号的方向。

2.2 复杂地形条件下的多AIRS联合定位

在复杂地形条件下，利用多个AIRS对目标点进行定位时，由于建筑物、山地以及树木等的遮挡，可能存在部分AIRS布设的位置不合理从而不能提供足够强大的视距传输的情况，而且由于目标点位置，也不能够对AIRS布设的位置进行调整，此时若直接使用所有AIRS进行定位，会导致目标点的定位误差增大，降低定位性能。因此在上述研究的基础上对算法进行了改进，提出了一种AIRS选择算法。对不同视距条件（莱斯因子取不同值）的角度域级联信道研究发现：

（1）对于视距条件差的AIRS，其级联信道的角度域特性如图2所示，基本呈现角度域信道的增益存在不止一个“极点”的特征；

图2 较差视距条件下信道角度域特性

（2）对于视距条件较好的AIRS，其级联信道的角度域特性如图3所示，也有可能存在多个“极点”，但是LoS路径对应的极点比其他极点的增益高。

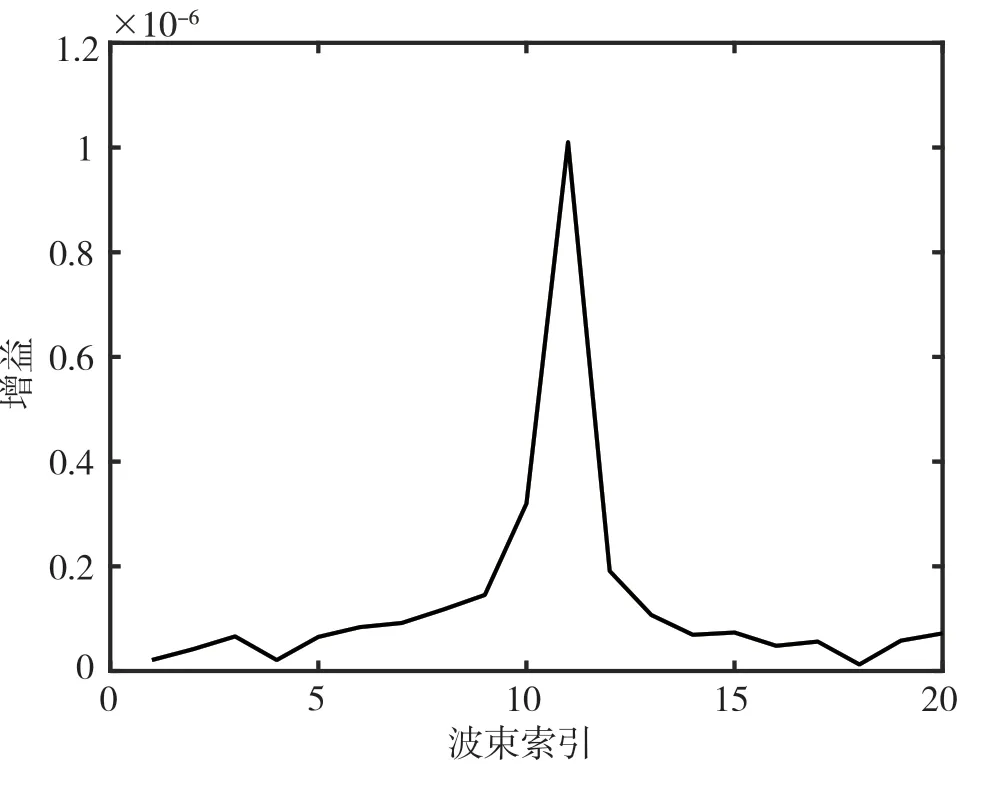
图3 良好视距条件下信道角度域特性

由此可以推断，当只有LoS路径时，其级联信道的角度域增益只存在LoS路径的一个极点。

基于上述分析，在定位时应当尽量选择视距条件较好的AIRS进行定位，因此提出多AIRS选择算法。

假设有I个AIRS可用于目标点定位，各个AIRS提前布设于确定位置。获取各个AIRS级联信道的角度域增益向量ai(i=1,2,…,I)，得到各个向量极点组成的向量pi(i=1,2,…,I)，计算LoS权重系数ki，其定义如下：

式中：ξi=Mτcos(αi)+1。定义AIRS的权重系数向量为k=(k1,k2,…,ki)，选择k中最大的两个权重系数（假设为kp和kq，并且kp>kq）所对应的AIRS索引q和p作为用于定位的基本集合，即τ=0.5λ，R={p,q}，找出k中最小权重系数（假设为kc），将kp和kq从k中移除，对于剩余的权重系数ki,i=1,…,I,i≠q,p，若满足ki≥ς*(kq-kc)+kc，则其对应的索引i可以加到集合R中，其中，系数ς∈[0.5,1)为ki距离kq的程度，若ς越接近于1则表示ki越接近于kq，其信道的LoS强度与第q个AIRS相差不大，可用于定位。随后重复上述步骤，依次遍历所有的ki最后确定R，使用集合R中元素对应的AIRS序号对目标点进行定位。

3 数值仿真

仿真如图4所示，场景中使用6个AIRS来进行定位。

图4 仿真模型

具体的参数设置如表1所示。

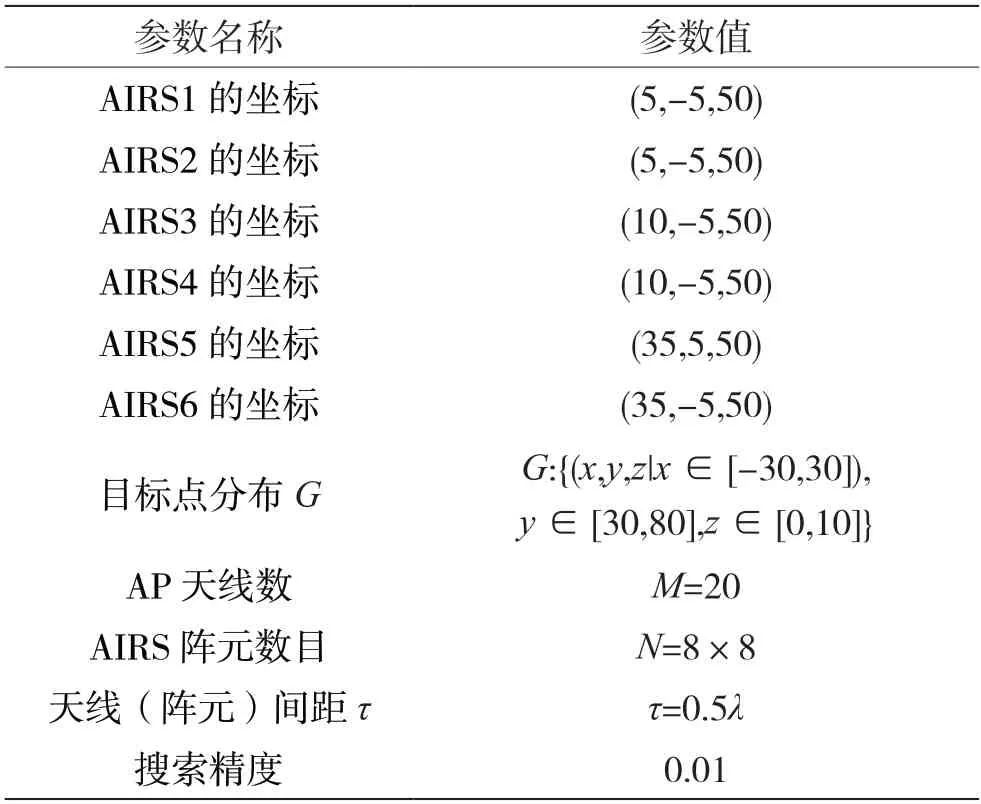
表1 参数设置

首先，仿真AoA测向算法的性能。使用第一个AIRS对目标点进行测向，本文研究了不同莱斯因子取值下AoA测向算法的角度估计性能。对于每一个莱斯因子κ的取值，进行1 000次实验，每次实验目标点的位置随机给出。目标点角度估计误差记为：

图5 角度误差估计趋势

其次，研究所提出的AIRS选择算法的性能，这里使用6个AIRS对目标点进行定位，进行1 000次随机实验，每次实验中目标点位置随机，其各个信道的莱斯因子也在0～30 dB范围内随机给出。主要比较两种方案。

（1）不做选择：不对AIRS进行选择，每次都使用6个AIRS同时对目标点进行定位。

（2）AIRS选择算法：每次实验中，使用所提出的AIRS选择算法选择合适的AIRS对目标点进行定位。

仿真结果如图6所示，对于所提出的算法其定位误差在1 m以内的累计概率为65%，2 m以内的累计概率为89%。而对于不做选择的方案，其定位误差在1 m以内的累计概率为35%，在2 m以内的累计概率为82%。此外，经计算AIRS选择算法的平均定位误差为0.99 m，而不做选择方案则为1.39 m。因此所提算法具备更好的定位性能。

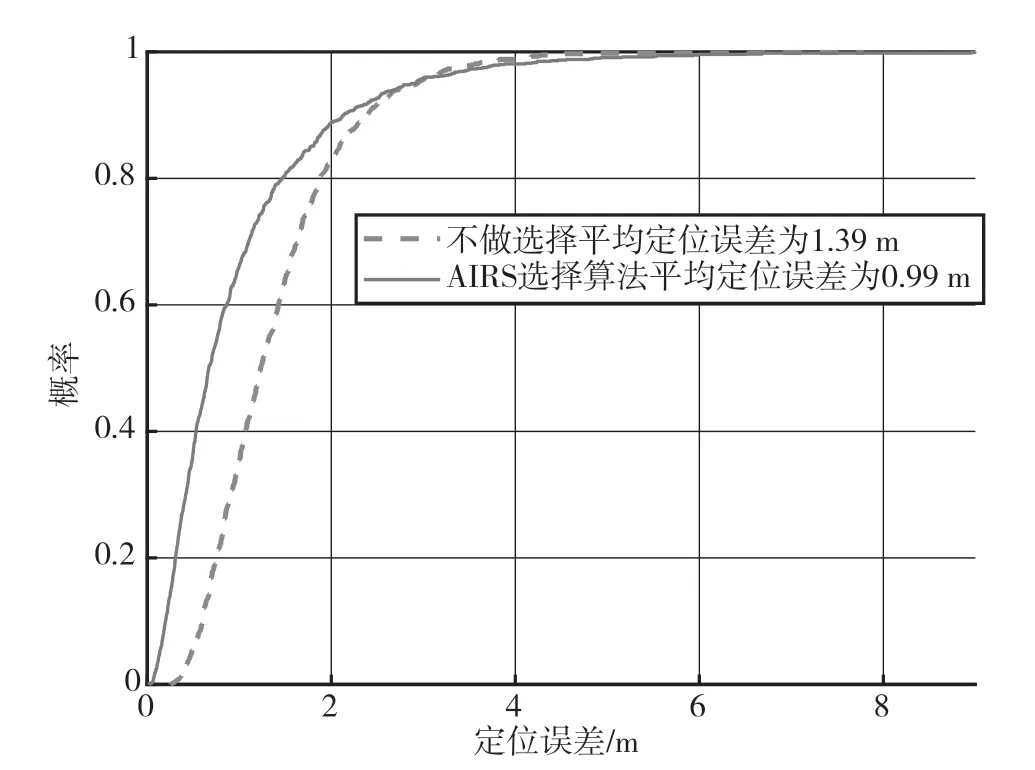
图6 定位误差概率

最后，研究在AIRS位置扰动情况下，所提算法的定位性能。在实际情况下，由于AIRS布设于空中（无人机上），其自身的位置受到环境、无人机GPS以及无人机本身悬停精度的影响可能存在一定的误差，将其称为位置扰动。假设第i个AIRS的坐标为由于悬停位置存在误差，故其真实位置为其中，和表示位置误差，均服从[0,r]内的均匀分布，r表示位置扰动系数。进行1 000次随机实验，为了研究位置扰动的影响，每次实验中莱斯因子取固定的值，同时，为了反映复杂地形条件，差异化设置各个AIRS级联信道的莱斯因子的取值，具体为κ1=0 dB，κ2=10 dB，κ3=10 dB，κ4=20 dB，κ5=20 dB，κ6=30 dB。本文分别研究了不同的扰动条件下所提算法的性能。如图7所示，对于每一个扰动系数的取值，对比了AIRS选择算法和不进行AIRS选择两种方案的性能。可以看到所提算法的性能要好于不做选择方案。因此在位置扰动条件下，所提算法可以提升目标点定位性能。

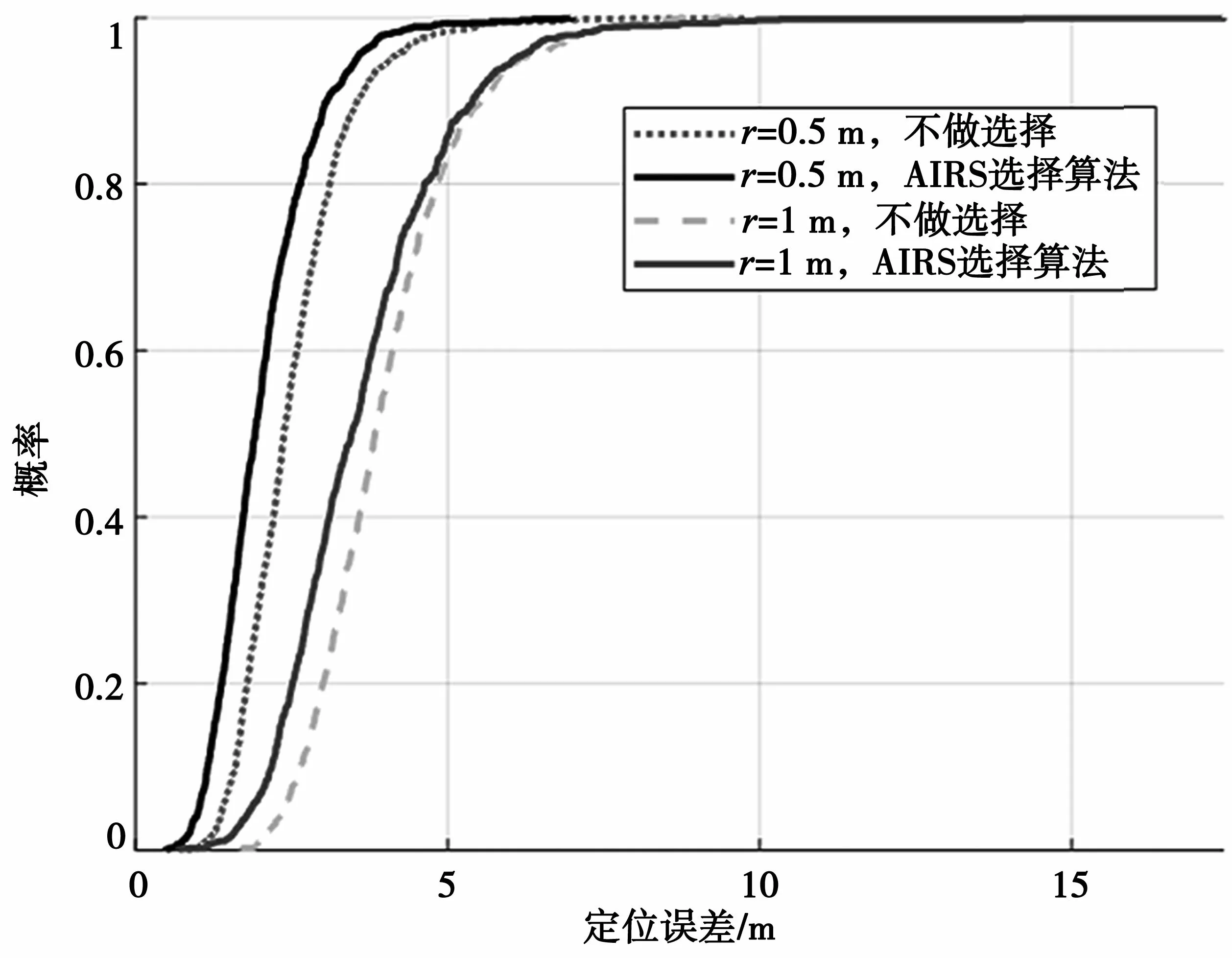
图7 定位误差概率

4 结语

IRS辅助下的无线通信系统将凭借低能耗、易部署等优势成为未来的一项关键技术，对传统定位技术也将带来意想不到的影响。本文在现有研究基础上提出多AIRS联合辅助定位策略，主要针对IRS的选择进行分析，从而达到提高定位精度的目的。目前IRS辅助下的定位技术研究成果很少，距离此项技术的成熟还有较大距离，因此如何真正将其合理应用，实现定位的智能化，还有待更加深入的研究与实践探索。