基于新型并行LMS算法的数字预失真器设计*

曾德军

（中国西南电子技术研究所，四川 成都 611731）

0 引言

现代通信系统对功率放大（Power Amplifier，PA）器的性能要求越来越高，特别是要求功放能够在保持较高效率的同时呈现良好的线性放大特性。然而，现实中功放硬件一般都具有一定的非线性和记忆效应，造成功放信号带内失真和带外频谱滋生，这些都将对通信系统造成严重影响。因此，功放线性化技术近年来逐渐成为一个研究热点。

数字预失真器（Digital Predistorter，DPD）作为一种切实可行的高效功放线性化技术，近些年已经得到了广泛的讨论和研究。数字预失真技术在处理码分多址（Code Division Multiple Access，CDMA）和正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）等这类具有较高峰均比（Peak to Average Power Ratio，PAPR）的信号时，可以在牺牲较小效率的条件下，达到功放的线性化目的，因此，在4G和5G通信系统中运用极其广泛。文献[1]、文献[2]、文献[3]、文献[4]和文献[5]提出了一些DPD的模型，其中，记忆多项式模型对功放的非线性特性和记忆效应都有较好的补偿效果[4,5]，是一种极具应用前景的功放预失真模型。相应地，很多自适应算法如最小均方（Least Mean Square，LMS）算法和递归最小二乘（Recursive Least Squares，RLS）算法也被应用于功放模型的辨识和DPD模型的参数计算。由于LMS算法更适合于硬件实现，因此本文将只针对LMS算法结构进行讨论。

然而，传统的DPD中使用的LMS算法面临实现资源消耗问题。传统算法都是基于复数滤波器结构的，在该方法下，进行一次简单的复数乘法就会消耗4个实数乘法器和3个实数加法器，自适应算法的实现复杂度会很大。这样的算法直接运用到现场可编程门阵列（Field Programmable Gate Array，FPGA）或者数字信号处理器（Digital Signal Processor，DSP）中实现时，会消耗大量的逻辑资源和面积，系统的吞吐率将无法得到提升。

为了解决以上问题，本文运用了一种新颖的基于3支路并行的实数滤波器结构，替代了传统DPD复数LMS补偿结构，该技术将复数滤波器的实部和虚部拆分开，重新组合成3路并行独立的处理支路，极大地缩减了运算资源。

1 DPD实现结构及传统LMS算法

本文中DPD采用间接学习结构，该结构如图1所示。预失真器和后逆模型都采用相同的DPD模型。x(n)为预失真器的输入，y(n)为功放的输出，d(n)为后逆模型估计输出的期望值，z(n)为后逆模型估计的输出实际值，e(n)为后逆模型估计的误差，G为PA增益补偿系数。后逆模型的参数值（后逆系数）可以通过自适应算法进行估计。获取后逆系数后，再将其复制到预失真器中，作为模型参数进行非线性补偿。

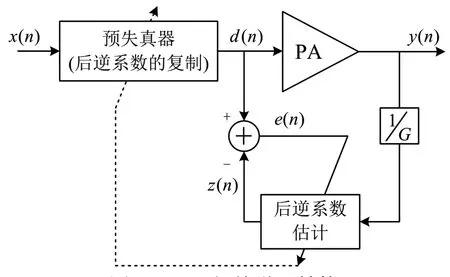
图1 DPD间接学习结构

本文先介绍DPD参数计算的传统LMS复数算法，然后再对该算法进行运算量的优化，推导出3支路并行实数LMS算法。不失一般性地，本文中的DPD采用最常用的记忆多项式模型进行建模。

假设PA的后逆模块可采用如下的记忆多项式模型表征：

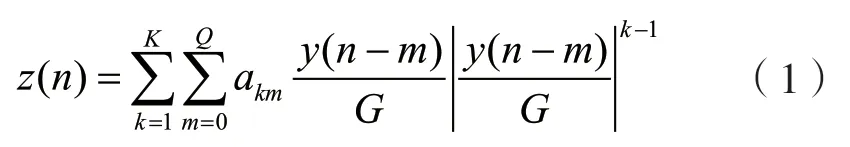
式中：m为模型记忆深度参量；Q为模型最大的记忆深度；k为多项式的阶数参量；K为模型的多项式的最高阶数；G为PA增益补偿系数；akm为模型系数，也是本文需要估计的目标参数。将目标参数组合成向量形式：

DPD的参数估计的目标便是对向量w的值进行估计。

令：

则式（1）可表达成横向滤波器形式：

求解系数w较为常用的为LMS迭代算法，其更新式如下：

（1）滤波输出：

（2）估计误差值：

（3）DPD模型参数的自适应更新方程：

式中：μ为LMS算法的迭代步长。

式（6）、式（7）和式（8）即为传统的DPD LMS更新算法。

2 三支路并行实数LMS算法

2.1 复数乘法器的并行结构优化

文献[6]、文献[7]、文献[8]和文献[9]提出了能够减少复数乘法器运算量的优化结构，其中3路并行结构（3CM structure）最为常用，本文将这种结构用到DPD的LMS算法中，用于模型的系数更新。

考虑直接实现一个复数乘法，任取向量w(n)中的标量w，用wI和wQ分别代表其实部和虚部；取向量u(n)中的对应位置的标量u，用uI和uQ分别代表其实部和虚部；则其复数乘法结果如下：

式（9）的虚部和实部等效为下面的变换：

式（10）和式（11）表征了复数乘法器的3路并行结构实现，3路运算分别为wI(uI+uQ)，(wI+wQ)uQ和(wI-wQ)uI。其中第1路可以在实部和虚部计算中复用，只用计算一次，从而节约运算量。这样新结构完成一次复数乘法只需要3次实数乘法操作和5次加法操作。而式（9）直接实现结构完成一次复数乘法需要4次实数乘法操作和2次实数加法操作。新结构仅通过增加3个实数加法器的代价，节约了1个实数乘法器。这种结构对于像FPGA这类乘法器资源极其宝贵的器件而言，是极有意义的。

2.2 复数LMS算法的并行结构优化

下面利用3支路结构思路，对复数LMS算法进行优化。

将DPD模型中所有变量都展开为同相分量和正交分量，分别用下标I和Q进行表征。输入向量和滤波器系数向量的复数表达式展开为：

按照3路并行结构类似方法，将输入向量和系数拆成如下3个并行实数系数支路：

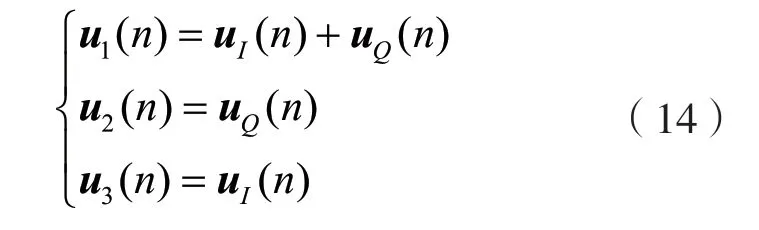
系数也拆成如下3个独立的变量：

3条支路的滤波输出为：

3条支路对应的2路估计误差值为：

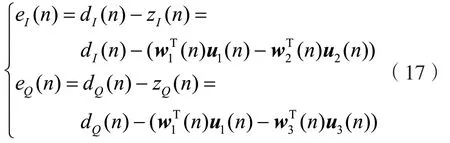
I路和Q路可以看成独立的两路滤波，可以利用MMSE准则分别求取系数更新方程。先考虑实部代价函数，其表达式为：

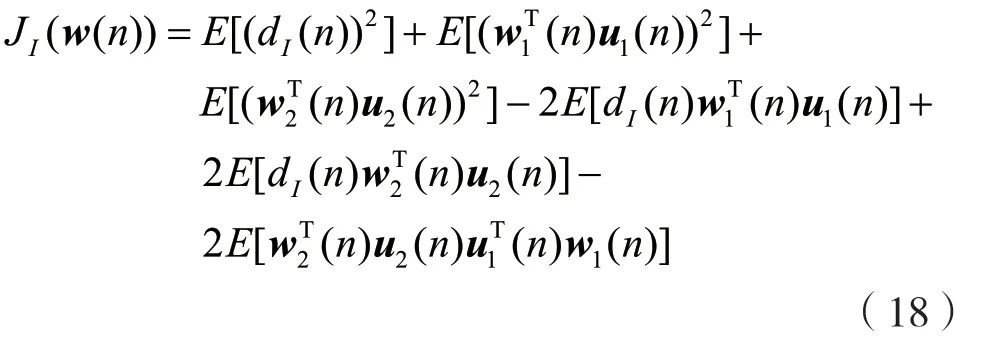
接下来，利用实部代价函数JI(w(n))的最下降法原理分别求解系数w1和w2。

系数w1的迭代公式为：

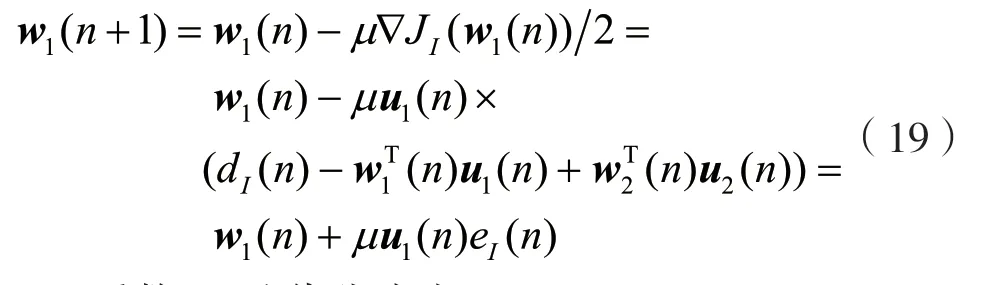
系数w2迭代公式为：

上面考虑的是实部分支的系数更新方程，现在考虑虚部分支的系数更新方程。由于实部和虚部对称同形，因此虚部分支的系数更新推导过程和实数分支完全一致。利用虚部代价函数最小原则，可以获得w1和w3的更新迭代式：

式（19）和式（21）都包含w1，将其合并，可以得到3支路并行LMS算法的系数更新方程：

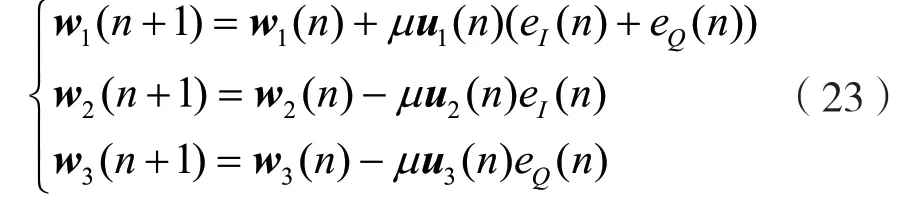
式（14）、式（16）、式（17）、式（23）共同构成了本文中提出的3支路实数并行LMS算法。相比于传统的复数LMS算法，新算法将单路复数权值滤波过程展开成了3路独立的实数滤波过程。

将上述算法过程应用到DPD中，新算法的整个滤波过程如图2所示。首先，输入复数向量需要按照式（14）进行分拆重组成3条支路输入；其次，按照式（16）、式（17）分别计算滤波输出和估计误差值；最后，通过式（23）进行3条支路独立的权值更新迭代。

图2 DPD的3支路并行实数滤波器实现结构

相对传统LMS算法，采用新的并行LMS算法能极大地减少乘法器运算量。假设滤波器阶次为M，输入信号和权向量都是M维向量。传统复LMS算法完成每次迭代需要进行8M次实数乘法（RM）和8M次实数加法（RA）操作。并行实值LMS算法完成每次迭代只需要经过6M次RM和6M+3次RA操作，运算量降低了约25%。

此外，相对传统LMS算法，新的并行LMS算法更适合在FPGA中实现。传统LMS算法是串行结构，而新算法是3条并行实现结构。并行结构在FPGA中可以带来很多收益，不仅可以减少系统资源的消耗量，还能提高系统处理的吞吐率，大大提升系统的执行速率。因此，3支路结构可以很好地满足实际需求。

3 系统测试结果

为了测试3支路并行LMS算法在数字预失真器中的效果，本文利用MATLAB进行了仿真验证。首先用并行LMS算法对DPD系统的记忆多项式模型参数进行估计；其次利用估计后的DPD和PA进行级联，测试整个DPD+PA系统的性能。实验结果表明，基于该算法的DPD能够有效地补偿PA的非线性效应和记忆效应。

DPD使用的记忆多项式记忆深度为4，多项式最高阶次为15。PA使用的是Wiener-Hammerstein模型。其模型参数为：

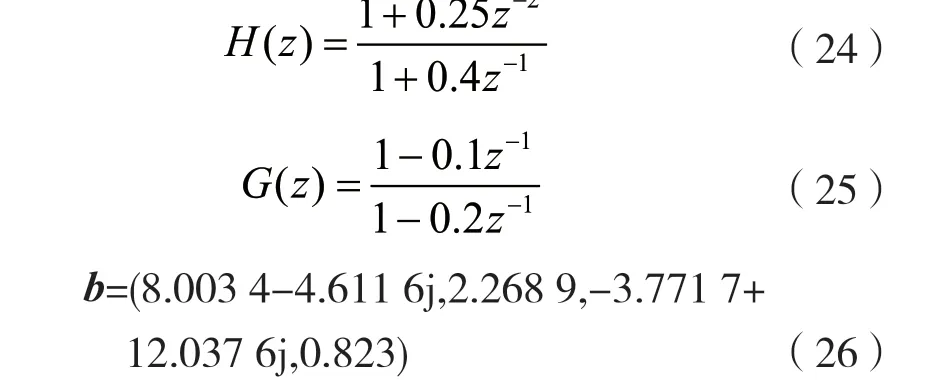
式中：H(z)和G(z)分别为模型的两个线性时不变系统函数；b为模型中的无记忆多项式系数。

输入到PA的测试信号是具有5M带宽的CDMA信号。

图3对比的是使用传统LMS算法和3支路并行LMS算法对DPD系统的模型参数进行估计的收敛曲线。虽然新算法相对传统算法收敛速度稍慢，但由于DPD预失真器对学习过程的时间并不敏感，因此是可以接受的。新算法最终的收敛误差性能和传统算法相近。

图3 传统LMS算法和并行LMS算法收敛曲线对比

图4显示了使用基于3支路LMS算法的DPD对PA进行预失真前后的系统AM-AM曲线。从图4中可以看出，PA呈现固有的非线性，但是当加入DPD后，系统的非线性特性得到了补偿。

图4 并行LMS进行DPD补偿前后的AM-AM曲线

图5比较了传统LMS算法和三支路LMS算法对DPD系统的补偿效果，图中（a）为未进行DPD补偿的结果；（b）为利用传统LMS算法进行DPD补偿的结果；（c）为利用并行LMS算法进行DPD补偿的结果。从图5中可以看出，两种算法都可以减小信号带内失真和系统带外频谱的杂散，3支路算法可以在以更少的算法复杂度和硬件开销的基础上达到几乎和传统LMS算法相同的预失真效果。

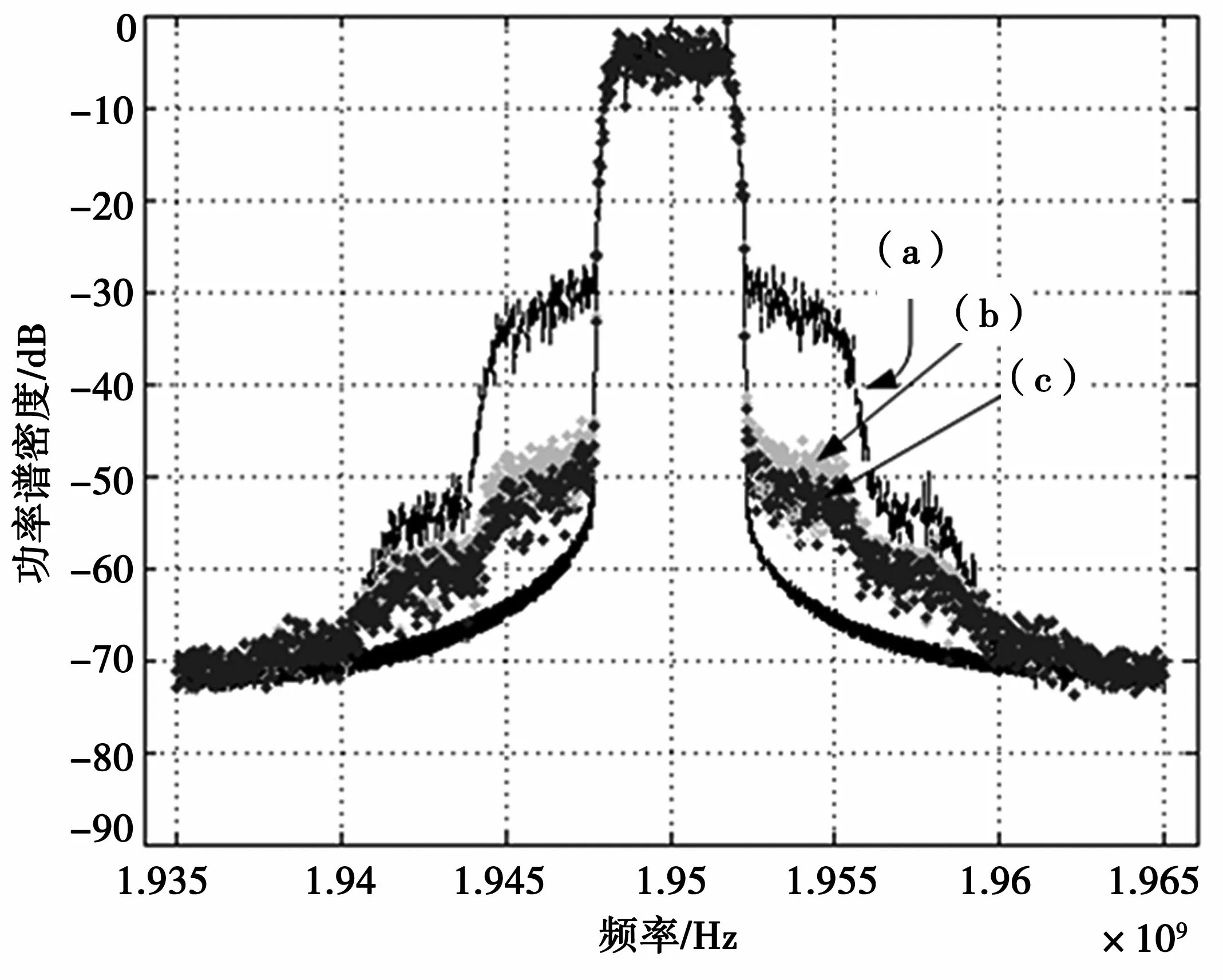
图5 功放输出CDMA功率谱

从上述仿真可见，新算法在优化了运算量的基础上，达到了和传统算法几乎相同的补偿性能。

4 结语

本文采用并行LMS算法有效地解决了DPD系统参数估计问题。相对于传统LMS算法，新算法复杂度更低，可以节约25%硬件实现资源。新算法采用并行结构，可以提高系统吞吐率。最后通过仿真验证，并行LMS算法稳定可行，DPD的非线性补偿性能和传统算法接近。因此，利用并行LMS算法在FPGA中实现DPD预失真器具有较大优势。