径向水平井自进式多孔射流钻头流场特性仿真*
2022-07-12张涛于怀彬黄欣李玉梅文涛王宁
张涛 于怀彬 黄欣 李玉梅 文涛 王宁
(1.北京信息科技大学高动态导航技术北京市重点实验室 2.中石油渤海钻探工程技术研究院 3.中石油冀东油田分公司钻采工艺研究院 4. 中石油塔里木油田分公司)
0 引 言
近年来,水力喷射径向钻孔技术已经被广泛应用在钻水平井、定向井、深穿透射孔、老井、洗井、解堵、钻水泥塞、切割套管等领域[1-3]。该技术已在中国、美国、加拿大、俄罗斯、阿根廷及玻利维亚等国家应用并取得了良好的效果[4-6]。
加拿大Penertrators公司以及美国ICT公司研制了水力喷射钻孔工具[7]。国内的中石化、中国石油以及中国石油大学(北京)的研究与应用也取得了不同的增产増注效果[8]。研究与应用结果表明:当钻孔深度超过15 m时,径向钻孔产能是常规射孔产能的2~3倍;可利用高压水射流导向的径向射流钻井技术,在垂直井筒方向形成长度为30~100 m、直径为25~50 mm的多个径向微孔[9-11];自进式多孔钻头可以产生多股射流或者旋转射流[12-13],它是径向水平井钻井技术中的关键部件,作业时在径向方向产生反冲力,对高压软管产生前向自进力的同时完成破岩钻孔,从而通过破碎岩石产生一定直径的微井眼。因此,面对勘探生产力度的加大,评估好径向水平井技术,将该技术经济有效地应用于老油田的挖潜,其市场前景广阔。
本文利用ANSYS-CFX软件建立自进式多孔射流钻头有限元数值模型,通过改变射流钻头前、后喷孔角度,以及前、后喷孔数量组合等参数,开展了钻孔器自进力、喷射速度以及三维流场特性分析,并与解析计算及试验结果进行比较。研究结果可为喷射钻头结构的改进以及水平径向射流钻进自进力的选择提供理论依据。
1 模型建立
1.1 自进式多孔射流钻头力学模型
根据动量定理,控制体在定常流动条件下水平方向的动量控制方程为[14]:
(1)
式中:ρ是流体密度,kg/m3;vx是水平方向速度, m/s;vn是瞬时速度, m/s;A是过流面积, m2;Fx是作用在控制体上水平轴方向的合力,N。
式(1)的左项表示控制体内水平方向上的动量变化,是喷嘴前、后孔出口处水平方向上的动量值减去入口处水平方向上的动量值,即如下式:
(2)
式(1)的右项表示作用于控制体边缘水平向上的矢量外力之和,得到:
(3)
式中:Fh是高压软管的拉力,N;pin是喷嘴的内压, Pa;pout是喷嘴的外压, Pa。
结合式(1)和式(2),可得:
(4)
从式(4)可得高压软管的拉力为:
(5)
射流喷嘴产生的自进力Fz可以表示为:
(6)
自进力可以由下式得出:
(7)
1.2 仿真建模
利用三坐标测量仪对多孔钻头进行测绘,可得模型参数:钻孔器的直径为30 mm,钻头总长度L为17.5 mm,内径d0为8.6 mm,外径d′为12.5 mm,前喷孔直径d2为0.5 mm,后喷孔直径d1为0.7 mm。根据测绘参数,建立水力喷射钻孔器几何模型,并通过三维建模软件的组合功能切分出流域模型,利用CFX建立水力喷射钻孔器有限元数值模型。因钻孔器前、后喷孔的直径小于微孔的直径,所以利用ANSYS-ICEM网格处理器对射流喷孔的三维流域进行分区网格划分。图1为流域模型网格。
模型计算假设:①模拟过程不考虑传热,能量方程处于封闭状态;②工作流体不可压缩且稳定;③不考虑重力。整个模拟环境中的工作流体采用密度为1 000 kg/m3的清水,泵的工作压力为50 MPa,排量为100 L/min。对射流喷管的模拟只考虑了进、出口和壁面的边界条件。设定边界条件后,调试求解器中的离散格式和松弛因子。
2 敏感性分析
2.1 多孔射流钻头前、后喷孔角度
在模拟过程中,底部围压p为40 MPa,前喷孔数为3,后喷孔数为6。前、后喷角设置如下:①前喷角θ2为20 °,后喷角θ1为30 °、35 °和40 °;②后喷角θ1为30 °,前喷角θ2为15 °、20 °和25 °。进口流量Q为40 L/min,研究前、后喷角对自进力和喷射速度的影响规律,结果如图2、图3和图4所示。
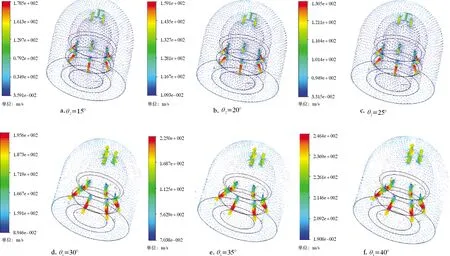
图2 钻孔器在不同前、后喷孔角度条件下的射流速度分布Fig.2 Distribution of jet velocity with different front and back nozzle angles

图3 后喷角对自进力和喷射速度的影响Fig.3 Influence of back nozzle angles on self-propelled force and jet velocity
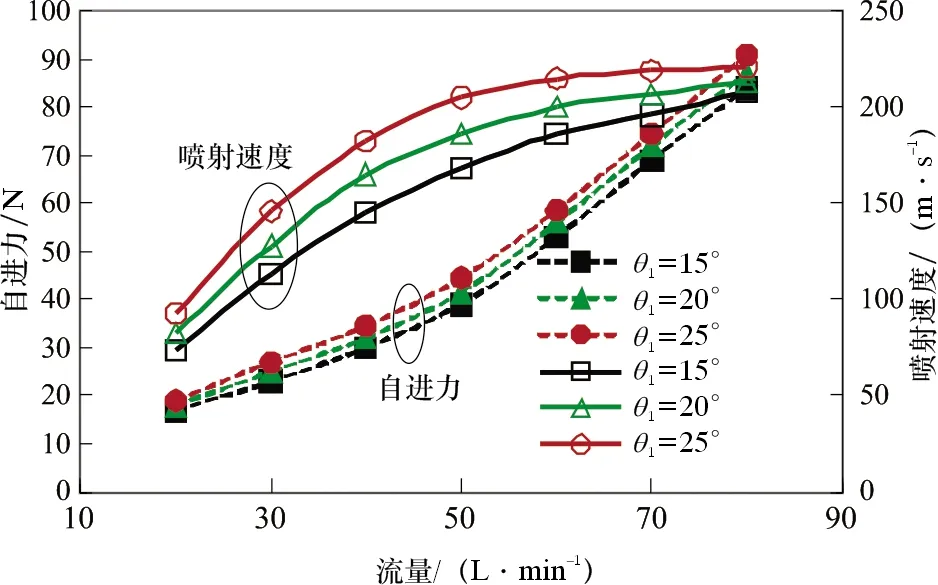
图4 前喷角对自进力和射流速度的影响Fig.4 Influence of front nozzle angles on self-propelled force and jet velocity
研究发现:随着前喷角的增大,自进力增加幅度较小,这说明前喷角对高压软管的牵引力影响较小,前喷角参数主要影响径向钻孔轨迹形态,因此仅在设计多孔喷嘴时用作参考。另外,随着流量的增大,自进力和射流速度有明显增加的趋势。如图3所示,自进力随着后喷角的增大而减小,喷射速度随着后喷角的增大而增加。为了获得较大的自进力和更大的径向孔眼,在多孔钻头设计中,后喷角不宜太大。因此,存在一个可以获得最佳自进力的后喷角,以完成高效的射流钻孔。
2.2 多孔射流钻头前、后喷孔数组合
模拟过程中,设置底部围压p为40 MPa,前喷角θ2为20°,后喷角θ1为30°。设置前、后喷孔数组合(F+B)包括:(1)3+4、3+5、3+6;(2)4+ 4、4 + 5、4 +6;(3)5+4、5+5、5+6共3类,并根据前、后喷孔数组合(F+B)分类建立三组仿真模型,如图5所示。3种不同喷孔数组合(F+B):3+6、4+6、5+6相应的流速矢量场分布如图6所示。
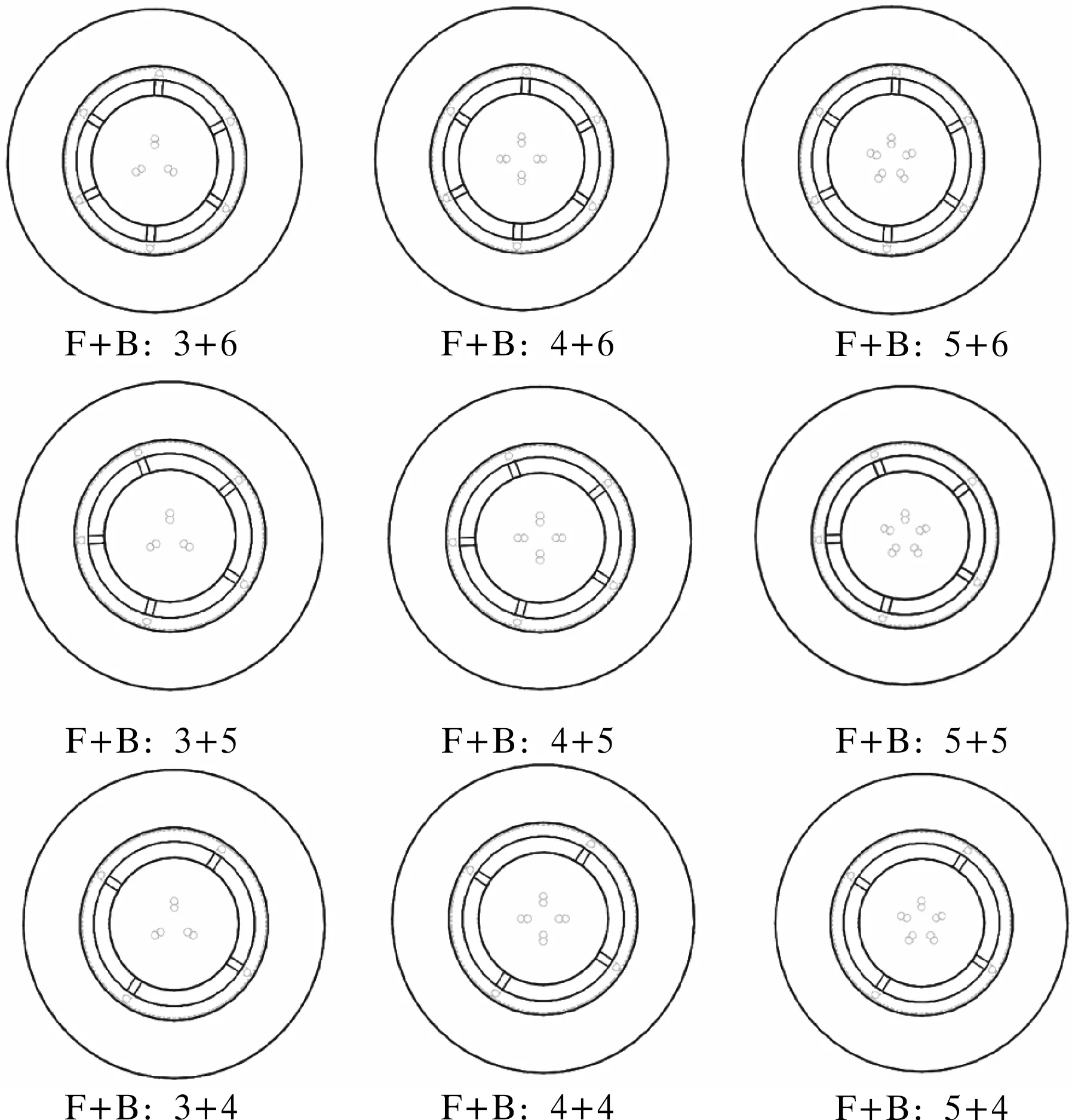
图5 不同前、后喷孔数(F+B)组合仿真模型Fig.5 Simulation models with different combinations of front and back nozzle numbers (F+B)

图6 不同喷孔数组合(F+B)相应的流速矢量场分布Fig.6 Distributions of flow rate vector field for different combinations of nozzle numbers (F+B)
图7为不同前喷孔数下流量与自进力的关系曲线。由图7可知,自进力随着流量的增加有大幅度增大的趋势,随前喷孔数的增加,自进力有明显减小的趋势。这是因为前喷孔数越多,出口压力越高,最后导致软管内出现更高的压力损失。

图7 前喷孔数对自进力的影响规律Fig.7 Influence of front nozzle numbers on self-propelled force
图8为不同后喷孔数下流量与自进力的关系曲线。由图8可知,自进力随着后喷孔数的增多增幅较小。这是由于后喷孔数越多,反向流量越大,破岩过程的驱动力越大,自进力则较小。因此,在保证自进力的前提下,为提高多喷嘴破岩效率,需要优化前、后喷孔数组合,以实现最佳径向射流钻井破岩性能。
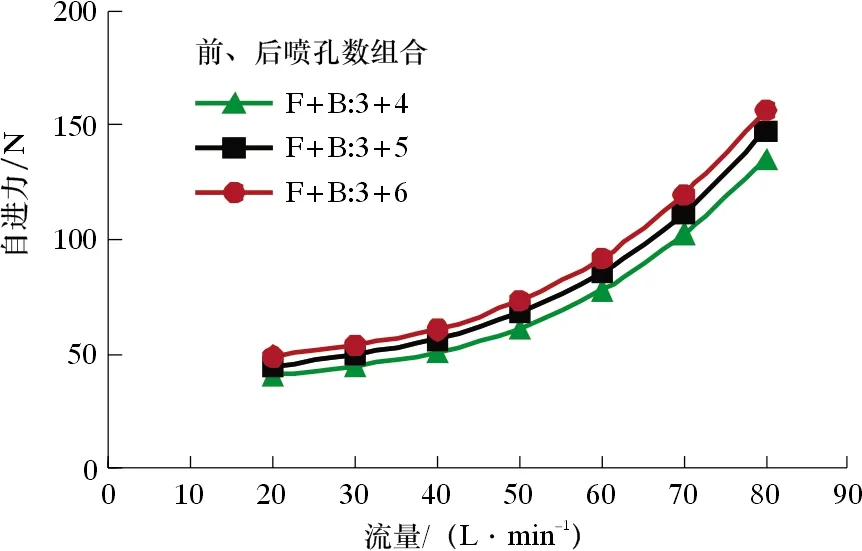
图8 后喷孔数对自进力的影响规律Fig.8 Influence of back nozzle numbers on self-propelled force
Fz-n和Fz-c分别为数值模拟结果和解析计算结果。不同前、后喷孔数组合下的自进力数值模拟结果与解析计算结果对比如图9所示。由图9可知,数值模拟结果与解析计算结果比较接近,表明本文所采用的数值模拟方法可以作为多孔射流钻头自进力评估依据。
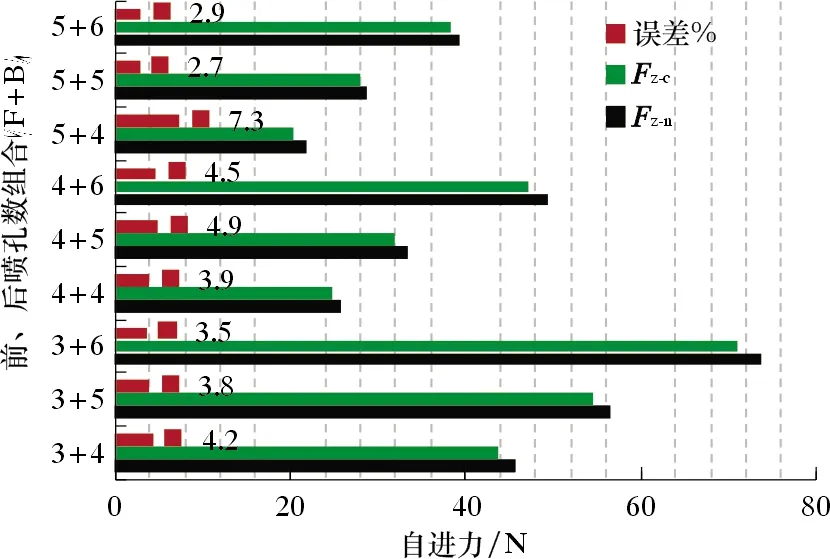
图9 自进力数值仿真与计算结果对比Fig.9 Comparison between simulation results and calculation results of self-propelled force
3 试验与结果分析
通过试验对数值仿真结果进行验证。确定试验条件与参数:试验泵压为40 MPa,排量为15~45 L/min;工作液为清水,密度为1 000 kg/m3,黏度为0.549 mPa·s;多孔喷嘴内径为20.0 mm,多孔喷嘴外径为12.2 mm。前向孔与后向喷孔数组合:3+6,前孔直径d2为0.50 mm,后孔直径d1为0.70 mm;前喷角θ2为20°,后喷角θ1为30°,油管外径为0.06 mm,将转向装置置于预定位置。
将水泥和水按一定比例混合成浆体,固定在套管外围形成水泥环,水泥环厚度为8 cm,高度为10 cm,水泥保持固化24 h后,采用多孔钻头在高压射流条件下进行套管开窗试验,开窗试验结果如图10所示。由图10可见,多孔钻头依靠自进力可以钻穿套管,开口平整均匀,边缘无毛刺和凸起,开窗质量完全满足现场工程要求。

图10 套管开窗试验结果Fig.10 Casing window test results
钻头自进力数值模拟结果(Fz-n)、解析计算结果(Fz-c)和试验结果(Fz-e)的对比如图11所示。由图11可知:Fz-n与Fz-e之间的差异较小,数值模拟精度可达97.31%;Fz-n与Fz-c之间的差异较小,数值模拟精度可达96.5%。这证明了数值模拟方法与试验方法、解析方法的计算结果高度契合。
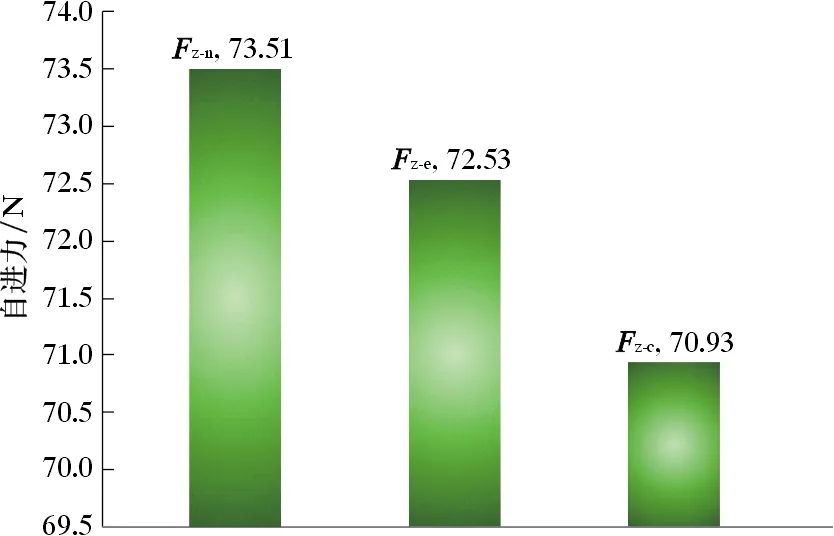
图11 自进力数值仿真、解析计算与试验结果对比Fig.11 Comparison between simulation results, calculation results and test results of self-propelled force
4 结 论
(1)自进力随前喷角的增大而增加的幅度较小。随着流量的增加,自进力和射流速度有明显增大的趋势。自进力随着后喷角的增大而减小,但喷射速度随着后喷角的增大而增加。
(2)自进力随着流量的增加有明显增大的趋势,随着前喷孔数的增多有明显减小的趋势,随着后喷孔数的增多增幅较小。因此,在多孔钻头设计时存在一个最佳前、后喷孔数组合。
(3)通过数值仿真模拟结果、解析计算结果和试验结果的对比发现:三者结果间的差异较小,平均精度为95.82%,而数值模拟结果与解析计算结果非常接近。这表明本文所采用的模拟方法可以作为多孔射流钻头水平径向射流钻进自进力选择的依据。
