基于CFD-DEM耦合几形管冲蚀磨损的模拟分析*
2022-07-12周大鹏马学东陈燕
周大鹏 马学东 陈燕
(辽宁科技大学机械工程与自动化学院)
0 引 言
天然气在管道输送过程中,会携带一些固体砂粒,砂粒在流体的携带下会对管道内壁产生冲击,尤其是弯头处[1-4],造成材料的损耗破坏,这种现象称为冲蚀磨损[5-7]。在众多标准管件中,几形管应用范围广且作用较大,该管件外观为“几”字形结构,别名为补偿器。由于流体中介质或外界环境气温等因素的影响,管道会产生热胀冷缩的情况,导致直线管道存在被拉断或扭曲的风险,为改变这一状况,就必须采用几形管件来保证管道的正常运行,另外又因其由4个弯头组成,失效率极高且失效形式较为复杂,所以,对几形管这一特殊管件进行冲蚀磨损的研究具有重要的意义。
当前,国内外学者对管道的冲蚀磨损问题做了大量研究。杨德成等[8]采用CFD软件计算弯管在气固两相流作用下的冲蚀磨损问题,得到了粒径和管径比与冲蚀速率的关系,并预测了最大冲蚀位置;钱东良等[9]通过CFD建立三通管件模型进行了气固两相流冲蚀磨损分析,研究了流向、流速和粒子流量等因素对冲蚀状况的影响;HONG B.Y.等[10]基于Fluent仿真数据,提出以雷诺数、密度比、粒径比和颗粒数目组成的关系式,进而预测弯管的冲蚀状况。由此可以看出,数值分析工具的运用对管道冲蚀磨损的研究具有积极意义,然而,大多学者采用的CFD软件有其自身的局限性,不能表征固体颗粒相的形状、碰撞以及位置等情况,其中颗粒间的碰撞和颗粒形状对冲蚀磨损的影响尤为重要[11-12]。为此,本文将采用CFD-DEM耦合,使仿真更趋于真实化。除了模拟方法外,目前文献大多是对一般性管件的研究,关于几形管冲蚀特性的分析却鲜有报道,又考虑到该管件具有较高的研究价值,因此本文将选用几形管作为研究对象。
本文通过CFD-DEM耦合并引入Archard wear模型,模拟了天然气携砂对几形管的冲蚀磨损行为,探究了不同参数对几形管的冲蚀磨损规律,分析了颗粒运动分布状态,预测了冲蚀位置和情况,并根据分析结果提出一些建议,以期能够对实际工程中管道设计和维护有所帮助。
1 数学模型
1.1 气相运动方程
为了预测几形管内气固两相流所造成的冲蚀磨损,气相运动对颗粒的影响至关重要,因此,计算流场将采用N-S方程,经计算颗粒浓度较小,可忽略空隙率,以节省计算资源,继而得到连续方程和动量守恒方程[13]:
(1)
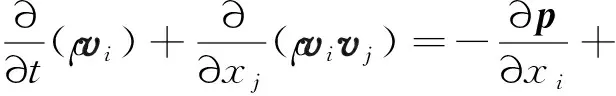
(2)
式中:ρ为气流密度,vi、vj分别为流体在i、j方向的速度,p为气流压力,g为重力加速度,μeff为标准k-ε湍流模型下流体的有效黏度。
1.2 颗粒相运动方程
经由耦合接口的数据传递,离散元模型中的颗粒在气相流体的作用下,颗粒做平动及转动运动,且还受到接触碰撞和重力的作用,因此,由牛顿第二定律得到其运动方程[14]:
(3)
(4)
式中:N为碰撞的颗粒数或壁面数,Fc,n,ij为法向接触力,Fc,t,ij为切向接触力,Ff为流体作用于颗粒的总力,ωi为颗粒的转动角速度,Ii为颗粒的转动惯量,Tc,ij为作用于物体上的力矩,Tr,ij为作用于物体上的扭矩。
对于颗粒之间、颗粒与管内壁面之间的接触碰撞过程的计算,选用EDEM中内含的Hertz-Mindlin(no slip)模型,该碰撞模型如图1所示。
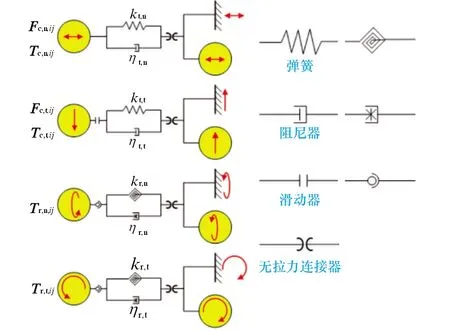
图1 碰撞模型Fig.1 Collision model
由图1可知,模型中每个碰撞力或力矩都被看作是弹簧或阻尼器,因此该模型又称为线性弹性-阻尼碰撞模型[15],在确保颗粒体系运动准确性的前提下,简洁高效地表达了颗粒碰撞过程中的受力变化。
1.3 冲蚀磨损模型
冲蚀磨损为流体携带颗粒以一定速度和角度冲击到物件表面,造成材料的损耗并形成凹坑的现象。过去,冲蚀磨损一般以冲蚀速率来表示,不能很好地表达这种磨损现象,因此,本文引入了Archard等提出的冲蚀磨损模型[16-17],材料表面的磨损以体积W形式来表征,且为EDEM软件中内置Archard wear模型功能,计算后的结果是以单位面积内冲蚀深度Δh来表达磨损量,具体公式如下:
(5)
(6)
式中:K为磨损系数,A为颗粒与管壁接触面积,Fn为颗粒对管壁的法向力,ΔL为颗粒在管壁上滑移的长度。
2 基于CFD-DEM耦合的气固两相流模型
2.1 耦合流程
针对气固两相流模型,采用Eulerian-Lagrangian耦合模型,即CFD-DEM。两者的耦合过程是一个瞬态双向数据传递的过程。首先,利用CFD计算一个时间步的流场信息,然后启动DEM进行相同时间迭代,通过耦合接口,流体运动信息传递到DEM中作用于颗粒,影响其运动,然后颗粒信息再反馈到CFD中作用于流体,若颗粒体积浓度过小,这种作用可忽略,如此,经过逐步循环迭代,实现全过程的瞬态模拟。耦合模拟流程如图2所示。

图2 耦合模拟流程Fig.2 Coupled simulation process
2.2 参数设置
首先,利用Soildwoks建立三维几形管模型,将模型导入到ANSYS Workbench中进行网格划分,然后设置模型的进口面为velocity-inlet,出口面为pressure-outlet,壁面命名为wall,最后进行全局网格划分,并对各个弯头进行加密,以便提高运算精度。网格划分结果如图3所示。图3中还对各个位置进行了名称标注。根据实际工况,天然气输运管道内颗粒粒径d的取值为0.14~0.30 mm,进口流速v的取值为4~12 m/s,颗粒质量流量为0.002 kg/s。

图3 几形管网格划分Fig.3 Mesh division of Ω-shaped pipe
EDEM中颗粒间或颗粒与壁面的接触模型选取Hertz-Mindlin(no slip)无滑移,冲蚀磨损采用Archard wear模型,根据材料属性选取磨损系数为10-12。其余参数设置[18]:颗粒密度2 650 kg/m3,管件密度7 800 kg/m3,颗粒泊松比0.4,颗粒剪切模量88 MPa,管件泊松比0.3,管件剪切模量7×10-4MPa,颗粒-颗粒静摩擦因数0.44,颗粒-颗粒动摩擦因数0.27,颗粒-颗粒恢复系数0.01,颗粒-管件静摩擦因数0.50,颗粒-管件动摩擦因数0.15,颗粒-管件恢复系数0.01,仿真总时长1 s。
2.3 模拟过程分析
按照上述参数要求完成了基于CFD-DEM耦合模拟几形管冲蚀磨损的仿真试验。现以颗粒粒径0.18 mm、进口流速10 m/s、颗粒质量流量0.002 kg/s仿真为例,结果如图4~图6所示。图4为气流压力云图。从图4可知:管件整体上的静压分布沿着管道的方向逐步降低,满足了气相流动的条件;在直管道部分的流体静压分布相对均匀,但在各个弯头处压力的分布极不均匀,即在各个弯头的外环壁面附近压力较大,在内环壁面附近压力较小,显然在弯头的内外侧之间形成了压力差。这种情况在离心力的作用下易形成二次流,造成能量损耗。

图4 气流压力云图Fig.4 Cloud chart of gas flow pressure

图6 气流速度矢量图Fig.6 Vector diagram of gas flow velocity
图5为气流速度云图。从图5可知,在压力差的作用下,气相速度整体上沿着管道的方向流动,但是可以发现,流体在弯头处拐弯时,内环侧流速较大,外环侧流速较小。这是内环侧压力较低,受到后面流体的冲挤,进而导致流速相对较大。结合图6的速度矢量图还可以发现,在各个弯头之间及弯头Ⅳ到出口处的区域,流体的流动之所以都是贴近管道的一侧壁面,这是因为漩涡流的存在,对流体造成了挤压,使其流动截面变小,也进而导致流速增大。漩涡流的产生原因是流体在流经弯头时具有惯性,且在弯头内环侧出口处进入直管段的部分区域为逆压梯度分布,非常容易产生边界层分离,由此流体的边界层脱离了壁面,并形成了与主流方向相背的回流,进而产生了漩涡流。综上,压力分布与速度分布相反,在弯头处,流体流过外环侧速度较小,但静压值较大;内环侧反之亦然。
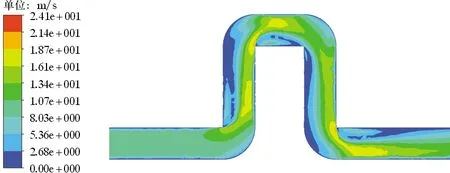
图5 气流速度云图Fig.5 Cloud chart of gas flow velocity
固体相颗粒在EDEM中的运动分布状态及冲蚀情况分别如图7和图8所示。
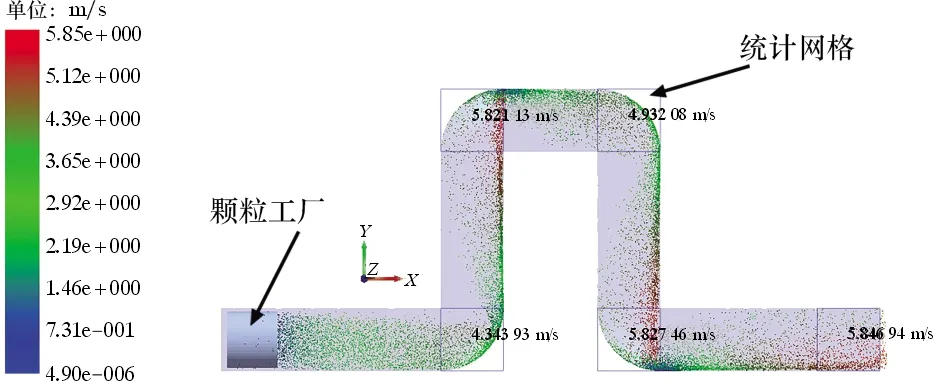
图7 几形管内颗粒运动分布Fig.7 Particles movement distribution in Ω-shaped pipe
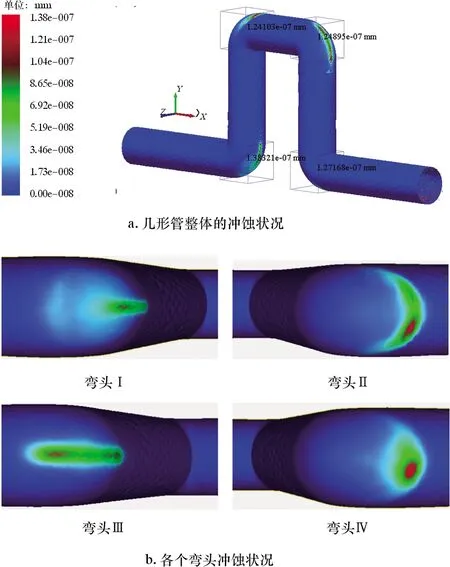
图8 几形管冲蚀磨损云图Fig.8 Cloud chart of erosion wear of Ω-shaped pipe
从图7可知:颗粒从进口处的颗粒工厂生成,在气流的作用下均匀地进入管道,颗粒在第一个水平直管段加速,到达弯头Ⅰ时,颗粒的最大速度达到了4.343 93 m/s,但抵达的同时,基本上都撞击在弯头的外侧内壁面上,紧接着,减速后的颗粒流运动到第1个垂直管段内,大部分颗粒紧贴管件内侧壁面,又一次完成了加速;到达弯头Ⅱ时,颗粒最大速度达到了5.211 30 m/s,但颗粒流在撞击到弯头的外环内壁面上,速度又一次将降了下来,接下来,颗粒拐进第2个水平直管段进行加速,但由于该管段过短,抵达弯头Ⅲ时,速度最大只是达到4.932 08 m/s,此时颗粒流经弯头Ⅲ时是贴近外环侧壁面运动的,以此类推,最后,颗粒在第3个水平直管段完成加速,以5.846 94 m/s速度冲出。由此可以看出,颗粒流的整个运动过程完全符合气相流体作用下的结果。从图8a可知,几形管在固体相颗粒流冲击的作用下,易发生冲蚀磨损的位置为4个弯头处。从图8b可以观察到各个弯头受到的冲蚀磨损程度及轮廓。造成这种差异性的原因是颗粒流不同的运动状态。弯头Ⅰ、弯头Ⅱ及弯头Ⅲ的冲蚀轮廓还较为规则,但是弯头Ⅳ冲蚀位置比较偏向一侧,并且冲击得较为集中。此外,各个弯头处都有一个矩形框,这是由后处理中的Grid Bin Groupgong功能设置的统计网格,这样可以在局部区域得到仿真结果,比如颗粒速度和最大冲蚀深度等。
3 结果及讨论
3.1 颗粒形状的影响
因为EDEM软件的优势,可以研究颗粒的形状对几形管冲蚀磨损的影响。为此,采用球形颗粒和带有角的非球形颗粒进行研究,如图9所示。
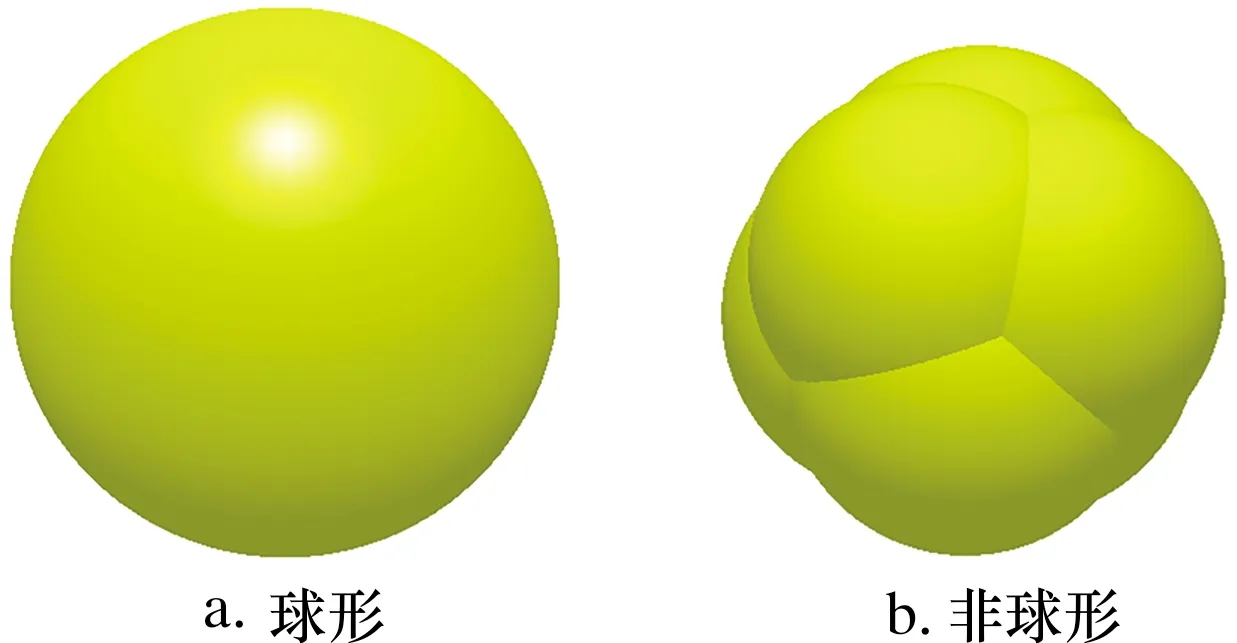
图9 颗粒形状Fig.9 Particle shape
虽然颗粒形状彼此不同,但是保证了颗粒的体积、质量及密度均相同。图10表示在相同工况下,不同颗粒形状对几形管各个弯头处最大冲蚀磨损深度的影响。从图10可以观察到,非球形颗粒下各个弯头的最大冲蚀深度都大于球形颗粒作用的冲蚀结果,其值(取4个弯头的平均值)增大32.1%。由此得出颗粒形状对冲蚀磨损有较大的影响。
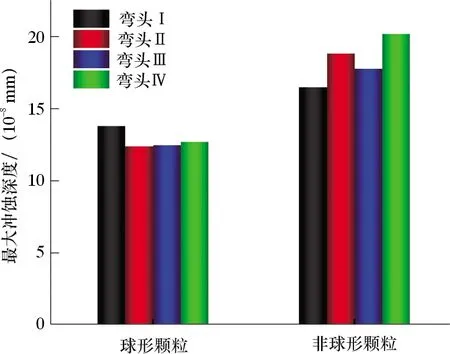
图10 颗粒形状对各个弯头最大冲蚀深度的影响Fig.10 Influence of particle shape on maximum erosion depth of each elbow
3.2 颗粒粒径的影响
根据实际工况,选取颗粒直径为0.14、0.16、0.18、0.20和0.30 m,在相同进口速度10 m/s、颗粒质量流量0.002 kg/s的条件下进行模拟计算,得到各个弯头处不同颗粒粒径与最大冲蚀深度的关系,如图11所示。
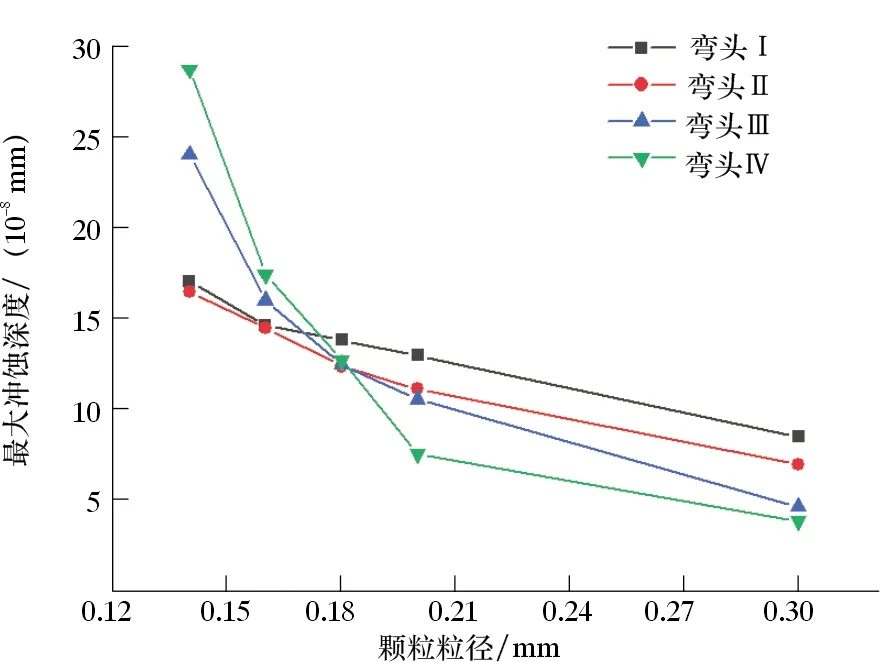
图11 颗粒粒径与最大冲蚀深度的关系Fig.11 Relationship between particle size and maximum erosion depth
从整体上看,无论是哪个弯头,最大冲蚀深度都随着颗粒粒径的增大而减小。其原因在于,颗粒粒径越大,相同的气相流速下携带作用越差,即颗粒速度越小,加之颗粒的质量流量保持不变,生成的颗粒数目减少,进而导致在相同时间内颗粒冲击到管内壁面上的次数越少,因此,最大冲蚀深度也都呈下降趋势。从图11还可以看出:颗粒粒径较小时,弯头Ⅳ的冲蚀深度最大,冲蚀磨损得最为严重;当颗粒粒径较大时,虽然4个弯头的最大冲蚀深度都趋于平缓,但是在磨损累积效应下,弯头Ⅰ会比另外3个弯头更早的出现破坏泄漏。针对弯头Ⅳ的最大冲蚀深度随粒径变化梯度大的现象进行了分析。随着颗粒粒径越大,颗粒数量越少,气流携带作用减弱,加之颗粒惯性力的作用,就越不容易在垂直管壁内的一侧形成料柱,进而对弯头Ⅳ的冲击不够集中,因此,随着粒径增大得到的最大冲蚀深度下降得最快,在粒径为0.18 mm之后,相比于其他弯头,其值都最小。图12为弯头Ⅲ与弯头Ⅳ之间直管段的截图,表示在同一时刻、相同条件下,粒径分别为0.14和0.30 mm的颗粒运动分布状态,以此形成对比来佐证上述观点。

图12 不同粒径下颗粒运动分布状态的对比Fig.12 Comparison of particle movement distribution with different particle sizes
3.3 进口流速的影响
设置进口速度分别为4、6、8、10和12 m/s,并控制颗粒粒径0.18 mm、质量流量0.002 kg/s等参数的一致性,得到不同进口流速下各个弯头最大冲蚀深度的变化规律,如图13所示。

图13 进口流速与最大冲蚀深度的关系Fig.13 Relationship between inlet velocity and maximum erosion depth
由图13可知,弯头Ⅰ、弯头Ⅱ及弯头Ⅲ的最大冲蚀深度随进口流速的增大而增大,但是弯头Ⅳ的最大冲蚀深度随着进口流速的增大,大致上是先增大后减小。这一情况的产生是由于随着气相流速的增加,颗粒在管件内运动的时间越短,单位时间内管道截面内通过的颗粒数量就会越少,越不容易在垂直管壁内的一侧形成料柱,相反地,颗粒速度不断增加,即动量增大,增大了冲蚀力度,因此,当两者都相对正好时,冲蚀磨损的程度最为严重,即在流速为8 m/s时,弯头Ⅳ的最大冲蚀深度达到峰值。图14为颗粒在管件内随着进口流速的变化,其驻留时间及最大速度的变化情况,由此可印证上述说法。
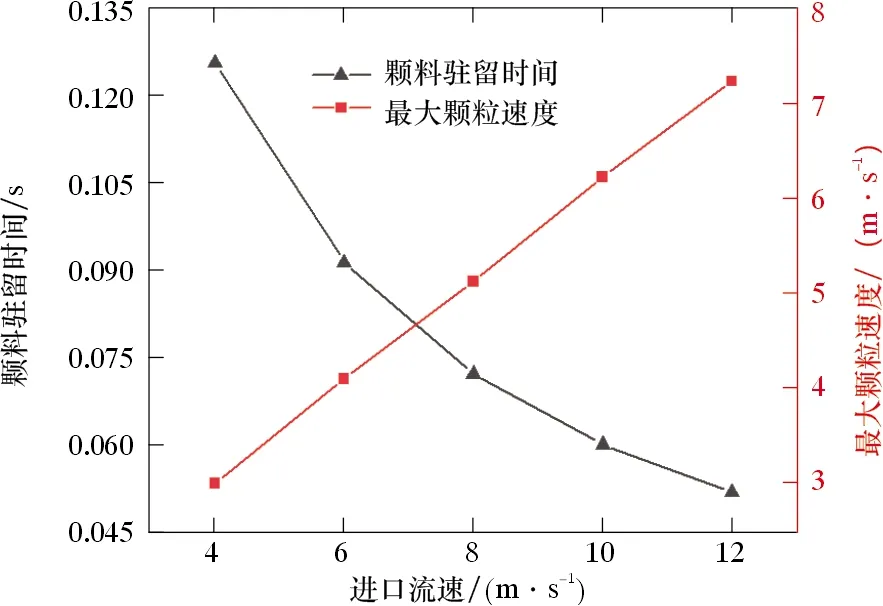
图14 颗粒驻留时间和最大颗粒速度随进口流速的变化规律Fig.14 Change rule of particle residence time and maximum particle velocity with inlet velocity
4 结 论
(1)基于仿真模型,分析了气固两相流在几形管中的运动特征,颗粒在气相流体的作用下加速,运动冲击到弯头处速度快速降低,如此反复多次,因此易被冲蚀破坏的区域是几形管4个弯头处,且都是弯头的外环侧壁面,形成的冲蚀轮廓面积各不相同。故检查及防护都应对这些区域重点关注。
(2)颗粒形状对冲蚀效果有显著影响,数据显示,非球形颗粒相比于球形颗粒,4个弯头的最大冲蚀深度平均增大了32.1%。
(3)从整体上看,最大冲蚀深度随着颗粒粒径的增大而减小。当颗粒粒径较小时,弯头Ⅳ的冲蚀磨损深度最大,更易出现破坏;当颗粒粒径较大时,4个弯头的最大冲蚀深度都相对平缓,但因磨损累积效应,弯头Ⅰ会更早出现破坏泄漏现象。
(4)最大冲蚀深度随进口流速的增大基本上呈线性增长的趋势,但弯头Ⅳ除外,因颗粒驻留时间和颗粒速度的共同作用,其值呈现出先增大后减小的特点,在进口流速为8 m/s时达到最大。
