封隔器仿生鳞片齿卡瓦微牙痕及稳定性研究*
2022-07-12李万钟邓冲徐建宁
李万钟 邓冲 徐建宁
(西安石油大学机械工程学院)
0 引 言
封隔器是在井筒中把不同油层和水层封隔并承受一定压差的井下工具[1]。卡瓦式封隔器被广泛应用于分层试油、采油、找水和堵水等各个油田技术领域中[2]。卡瓦在封隔器锚定时起到支撑封隔器、锁定胶筒的作用[3],是保证封隔器工作可靠性的重要元件之一。
油井套管属于薄壁件,由于楔形面使卡瓦径向扩张、挤压套管,在卡瓦牙与套管接触面会形成咬痕,过大的嵌入深度有可能会导致套管被挤裂、失效、易被腐蚀[4],而且会严重影响封隔器的二次封隔,致使解封困难或无法解封。因此,在保证封隔器正常工作的情况下,降低卡瓦对套管壁的损伤程度,即减小卡瓦在套管上产生的牙痕深度,就要不断对卡瓦进行优化[5]。
自然界的生物体表经过三十多亿年的演化发展[6],各种结构奇特、性能卓越、功能优异的表面结构逐渐应运而生,已经成为摩擦学科研人员重要的仿生研究对象。蛇类在快速移动爬行时,主要依靠覆瓦状排列的腹鳞提供前进的动力。蛇在爬坡时,其腹部鳞片会张开一定的角度,增大与粗糙地面相对运动所产生的摩擦力。当鳞片相对于地面的倾斜角度越大,摩擦力就越大,因而使蛇爬坡时能够获得足够的前进动力[7]。
本文所研究的封隔器卡瓦牙通过模仿蛇腹部鳞片形状,建立仿生鳞片齿卡瓦模型,运用有限元数值模拟和正交优化的方法得到其最佳牙型结构参数,并与常规齿卡瓦进行对比,探究其应力和形变规律,得到可减轻套管表面牙痕深度的仿生鳞片齿卡瓦。
1 卡瓦与套管无黏着法向接触的评估方法
根据接触力学理论,法向接触问题可表述为:由于力垂直作用于两个物体的表面而造成它们相互接触[8]。在纯法向接触问题中,假设接触区域没有摩擦力出现,同时暂且忽略黏着力。
1.1 常规卡瓦牙与套管接触模型
在研究单个卡瓦牙齿与套管的接触问题时,可看作是两个弹性体之间的接触,其中将套管视作是一个弹性半空间体,如图1所示。
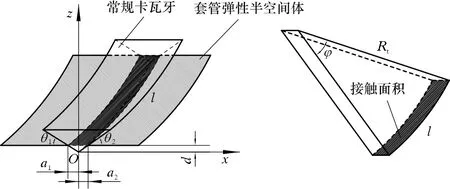
图1 常规卡瓦牙与弹性套管半空间体接触Fig.1 Conventional slip tooth contact with elastic casing half space
由图1的几何关系可以得出:
(1)
式中:a1、a2为接触半宽,mm;θ1、θ2为接触夹角,(°);d为压入深度,mm;l为接触弧长,mm;Rt为套管内半径,mm;φ为接触弧长对应的圆心角,(°)。
从图1可以看出,接触面为一个曲面,则接触面积S为:
(2)
假设卡瓦牙与套管的接触应力分布在一个特征长度为D(D=a1+a2)的有限表面区域内,则这个区域成为严重变形区域,如图2所示。此时,整个半空间体的总体变形和应力与尺寸为D的体积在三维空间的总变形和应力属于同一数量级。这个体积(约为D3)就是能量和力分布的主要空间[8]。

图2 弹性套管半空间体的严重变形区域Fig.2 Severe deformation region of elastic casing
于是应变量ε为:
(3)
作用力F为:
(4)
式中:E*为等效弹性模量,MPa[8]。
式中:E1、E2分别为卡瓦和套管的弹性模量,MPa;υ1、υ2分别为卡瓦和套管的泊松比。
若弹性套管半空间体发生了塑性变形,σo≈3σc,则法向力FN为:
(5)
式中:σo为弹性套管半空间体的硬度,MPa;σc为弹性套管半空间体的屈服应力,MPa。
1.2 仿生鳞片卡瓦牙与套管接触模型
同样,将鳞片齿卡瓦牙与套管的接触也看作是两个弹性体之间的接触,其接触模型如图3所示。

图3 鳞片齿卡瓦牙与弹性套管半空间体接触Fig.3 Scale slip tooth contact with elastic casing half space
从图3可以看出,接触面呈半椭圆形状,则接触面积S为:
(6)

假设卡瓦牙与套管的接触应力分布在一个特征长度为D(D=a或D=2c)的有限表面区域内,则这个区域成为严重变形区域。
应变量ε为:
(7)
鳞片状卡瓦牙与弹性套管半空间体接触的作用力F为:
(8)
式中:θ为接触夹角,(°)。
在塑性区域,σo≈3σc,可以得到法向力FN为:
(9)
2 卡瓦有限元三维模型建立
2.1 模型建立与材料选择
2.1.1 常规齿和仿生鳞片状卡瓦牙型结构参数对比
常规齿卡瓦牙型结构参数如图4所示。其中β为卡瓦牙倾角,α为卡瓦牙顶角,b为卡瓦牙宽,γ为卡瓦锥角。本文研究的卡瓦模型适用于ø139.7 mm(5in)石油套管,套管壁厚7.72 mm。
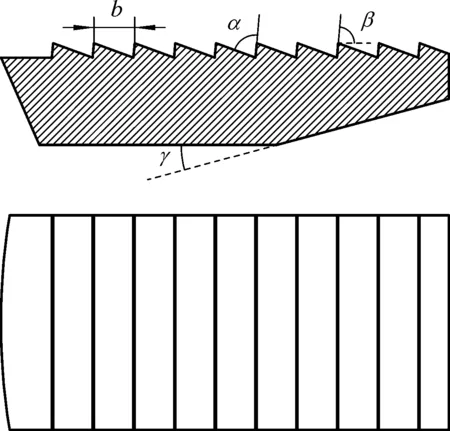
图4 常规齿卡瓦牙型结构参数Fig.4 Structural parameters of conventional slip tooth
仿生鳞片齿卡瓦的牙型结构参数如图5所示。其中β′为卡瓦牙倾角,α′为卡瓦牙顶角,b′为卡瓦牙宽,γ′为卡瓦锥角。相比于常规齿卡瓦,仿生鳞片齿卡瓦增加了在鳞片齿齿高方向投影下的长半轴R和短半轴r两个参数,且R=b′。当r

图5 仿生鳞片齿卡瓦牙型结构参数Fig.5 Structural parameters of bionic scale slip tooth
2.1.2 常规齿和仿生鳞片齿卡瓦三维模型
分别建立封隔器常规齿卡瓦模型和仿生鳞片齿卡瓦模型,如图6所示。

图6 卡瓦三维有限元模型Fig.6 Three-dimensional finite element model of slips
建立如图7所示的锥体、卡瓦、套管和刚性斜面体三维接触模型。模拟实际工况中,锥体在外加载荷的作用下推动卡瓦沿Y轴方向移动,当达到预定坐封载荷时,卡瓦牙咬入套管内壁,坐封完成[1]。选取单瓣卡瓦并截取一定长度和圆弧宽度的套管和锥体简化模型进行有限元仿真,这样可大大节省计算工作量和时间。锥体、卡瓦和套管的材料参数如表1所示。其中卡瓦的力学参数要大于套管的力学参数[9]。

图7 锥体-卡瓦-套管三维接触有限元模型Fig.7 Three-dimensional finite element model of contact between cone, slip and casing

表1 锥体、卡瓦和套管的材料参数Table 1 Material parameters of cone, slip and casing
2.2 网格划分与边界条件设置
卡瓦网格划分如图8所示。两种齿状卡瓦都采用C3D4(四节点线性四面体)单元进行网格划分,并且为确保计算精度,进一步对卡瓦齿与套管接触部分的网格进行加密。

图8 卡瓦网格划分Fig.8 Mesh division of slips
锥体-卡瓦-套管三维接触有限元模型的网格划分和边界条件设置如图9所示。其中套管模型采用扫掠网格划分技术,锥体模型采用结构化网格划分技术,均选择C3D8R(八节点六面体线性减缩积分)单元;斜面体模型设置为刚体,在进行网格划分时采用Quad(四边形)单元。由于实际工况中套管外壁用水泥浆固定,在套管外壁施加完全固定约束,在锥体上表面施加沿X方向的坐封载荷,并约束其内表面在Y方向和Z方向的自由度,在楔形面的作用下使卡瓦咬紧套管。

图9 锥体-卡瓦-套管三维模型网格划分和边界条件设置Fig.9 Mesh division and boundary conditions of three-dimensional contact between cone, slip and casing
卡瓦咬入套管过程属于接触非线性问题,套管发生局部塑形变形属于材料非线性问题,故该变形过程属于结构非线性问题[10]。锥体-卡瓦-套管三维接触模型主要涉及卡瓦与套管、卡瓦与锥体和卡瓦与刚性斜面体的接触,其法向接触属性均为“硬接触”,切向接触摩擦模型均为“库仑摩擦”,并用摩擦因数来表示。
3 结构参数优化和仿真结果分析
3.1 仿生鳞片齿卡瓦牙型结构参数优化
以卡瓦牙在套管内表面产生的应力和径向位移U(即牙痕深度)作为目标参量,把卡瓦牙倾角β′=90°和卡瓦锥角γ′=15°作为固定结构参数,利用有限元分析软件分别对鳞片状卡瓦牙顶角α′、长半轴R和短半轴r几个牙型结构参数进行了数值模拟优化,以确定出最佳牙型结构参数组合。
3.1.1 卡瓦牙顶角α′变化时目标参量的变化规律
对锥体-卡瓦-套管系统开展接触非线性有限元计算,当β′=90°、γ′=15°、R=r=5 mm时,分别取卡瓦牙顶角α′=66°、68°、70°和72°,比较套管的Von Mises应力值、径向位移U值和卡瓦与套管的接触面积S,数值模拟结果如表2所示。

表2 卡瓦牙顶角α′变化时目标参量的变化规律Table 2 Change rule of target parameters with different slip tooth apex anglesα′
从表2可以看出,当卡瓦牙顶角α′=70°时,套管的径向位移和Von Mises应力最小。但从整体上看,卡瓦牙顶角的变化对套管的径向位移和Von Mises应力影响较小。同时,随着卡瓦牙顶角的逐渐增大,卡瓦与套管的接触面积S逐渐减小。综合分析,取α′=68°、70°和72°作为优化卡瓦牙顶角。
3.1.2 卡瓦牙长半轴R变化时目标参量的变化规律
当β′=90°、γ′=15°、α′=70°、r=5 mm时,分别取R=5、6、7和8 mm,鳞片齿为半椭圆形,比较套管的Von Mises应力值、径向位移U值和卡瓦与套管的接触面积S,数值模拟结果如表3所示。

表3 卡瓦牙长半轴R变化时目标参量的变化规律Table 3 Change rule of target parameters with different slip tooth long semi-axis R
从表3可以看出,当卡瓦牙长半轴R=5 mm时,套管的径向位移和Von Mises应力最小,即卡瓦在套管上产生的牙痕深度最浅。同时,随着卡瓦牙长半轴的逐渐增大,卡瓦与套管的接触面积S逐渐增大。综合分析,取R=5 mm作为优化卡瓦牙长半轴。
3.1.3 卡瓦牙短半轴r变化时目标函数的变化规律
当β′=90°、γ′=15°、α′=70°、R=5 mm时,分别取r=3、4、5和6 mm,鳞片齿为半椭圆形,比较套管的Von Mises应力值、径向位移U值和卡瓦与套管的接触面积S,数值模拟结果如表4所示。

表4 卡瓦牙短半轴r变化时目标参量的变化规律Table 4 Change rule of target parameters with different slip tooth short semi-axis r
从表4可以看出:当卡瓦牙短半轴r=3 mm时,套管的Von Mises应力最小;当卡瓦牙短半轴r=4 mm时,套管的径向位移最小,即卡瓦在套管上产生的牙痕深度最浅。同时,随着卡瓦牙短半轴的逐渐增大,卡瓦与套管的接触面积S几乎不变。综合分析,取r=3和4 mm作为优化卡瓦牙短半轴。本文中所考虑的J55套管材料为弹塑性本构模型,根据塑性增量(塑性流动)理论,由于载荷继续的增大,材料经过屈服阶段后又会恢复抵抗变形的能力,即发生了加工硬化。此时材料会产生新的弹性和塑性变形,随着塑性变形的发生,屈服应力会增大形成新的屈服面。因此在有限元模拟中套管内表面会出现大于材料屈服极限的应力。
对上述所选出的卡瓦牙倾角、卡瓦牙长半轴和短半轴的优化牙型结构参数进行组合,结果如表5所示。

表5 牙型结构参数组合Table 5 Combinations of tooth structural parameters
从组合1到组合6的各参数对套管最大Von Mises应力、套管最大径向位移影响的变化曲线如图10所示。
从图10可以明显看出,组合顺序号3各参数下的套管最大Von Mises应力值和套管最大径向位移值最小,即在β′=90°和γ′=15°为固定结构参数下,R=5 mm、r=3 mm和α′=72°是仿生鳞片齿卡瓦最佳牙型结构参数组合。

图10 不同组合序号下套管最大Von Mises应力和最大径向位移的变化曲线Fig.10 Variation curves of maximum Von Mises stress and maximum radial displacement of casing with different combination numbers
3.2 常规齿和仿生鳞片齿卡瓦有限元仿真结果 对比分析
卡瓦抱紧套管时,卡瓦牙挤压套管并咬入套管壁中,牙齿在套管表面留下了纹理清晰的咬痕,当载荷达到一定值时,咬痕部位会发生塑性变形[11]。已有文献优化得出常规齿卡瓦最优结构参数组合为:β=85°,α=75°,b=8 mm,γ=15°[12]。由3.1节优化出的仿生鳞片齿卡瓦最佳结构参数组合为:β′=90°、γ′=15°、R=5 mm、r=3 mm和α′=72°。对优化后的两种卡瓦分别开展有限元数值模拟仿真,得到卡瓦的Von Mises应力云图,如图11所示。套管的Von Mises应力云图和径向位移U云图,分别如图12和图13所示。

图11 不同卡瓦的Von Mises应力云图Fig.11 Cloud chart of Von Mises stress of different slips
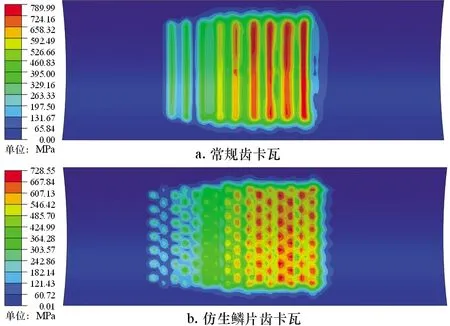
图12 不同卡瓦咬合套管的Von Mises应力云图Fig.12 Cloud chart of Von Mises stress on casing with different slips

图13 不同卡瓦咬合套管径向位移U云图Fig.13 Cloud chart of radial displacement Uof casing with different slips
从图11可以明显看出卡瓦牙齿受力的非均匀性,两种卡瓦与锥体接触端的齿所承受的应力非常大,最大Von Mises应力达到约835 MPa,同时,越远离锥形面的齿所承受的应力越小。
由图12和图13可知,两种齿状卡瓦在套管上产生的应力和变形也同样遵循从右往左依次减小的规律。经对比发现:优化结构参数后的仿生鳞片齿卡瓦在套管上产生的最大Von Mises应力为728.55 MPa,小于常规齿卡瓦在套管上产生的最大Von Mises应力789.99 MPa;经优化结构参数的仿生鳞片齿卡瓦咬合套管后且在套管上产生的最大径向位移,即牙痕深度为0.250 6 mm,小于常规齿卡瓦在套管上产生的牙痕深度0.308 0 mm。由此可以得出结论:优化结构参数之后的仿生鳞片齿卡瓦比经优化后的常规齿卡瓦在套管内表面产生的应力和牙痕深度要小,且应力减小了7.8%,牙痕深度减小了18.6%,证明优化牙型结构参数后的仿生鳞片齿卡瓦具有减轻牙痕的作用。
4 摩擦因数对卡瓦与套管非线性接触的影响
卡瓦作为封隔器的关键部件,既要确保坐封的稳定性,又要满足一定的锚定效果及承压能力[13-14]。卡瓦与套管之间的接触行为是本文研究的重点,两接触面间的摩擦因数是影响封隔器锚定效果的重要因素,通过有限元模拟探究卡瓦与套管接触面摩擦因数f分别为0.10、0.15、0.20、0.25、0.30、0.35和0.40时,卡瓦对套管内壁应力和应变的影响,以及对卡瓦与套管接触压力的合力(CFN)、摩擦应力的合力(CFS)和接触面积(CAREA)的影响。
改变优化结构参数后的常规齿和仿生鳞片齿卡瓦与套管接触面的摩擦因数,其在套管上产生的最大Von Mises应力和最大径向位移U值的变化曲线如图14所示。

图14 不同摩擦因数对卡瓦与套管接触的应力和位移的影响Fig.14 Influence of friction coefficient on stress and displacement between casing and slip
从图14可以看出:对于常规齿卡瓦,摩擦因数的改变对套管的最大Von Mises应力和径向位移的影响较大;随着卡瓦与套管接触面摩擦因数的增大,套管的最大Von Mises应力和径向位移也逐渐增大。而对于仿生鳞片齿卡瓦,摩擦因数的变化对套管最大Von Mises应力和径向位移的影响较小,这说明仿生鳞片齿卡瓦比常规齿卡瓦的稳定性好。
改变优化结构参数后的常规齿和仿生鳞片齿卡瓦与套管接触面的摩擦因数f,得到不同摩擦因数下卡瓦与套管接触压力的合力(CFN)、摩擦应力的合力(CFS)和接触面积(CAREA)与接触时间的关系曲线,如图15~图17所示。

图15 不同摩擦因数下卡瓦与套管接触压力的合力Fig.15 Resultant force of contact pressure between slip and casing with different friction coefficients
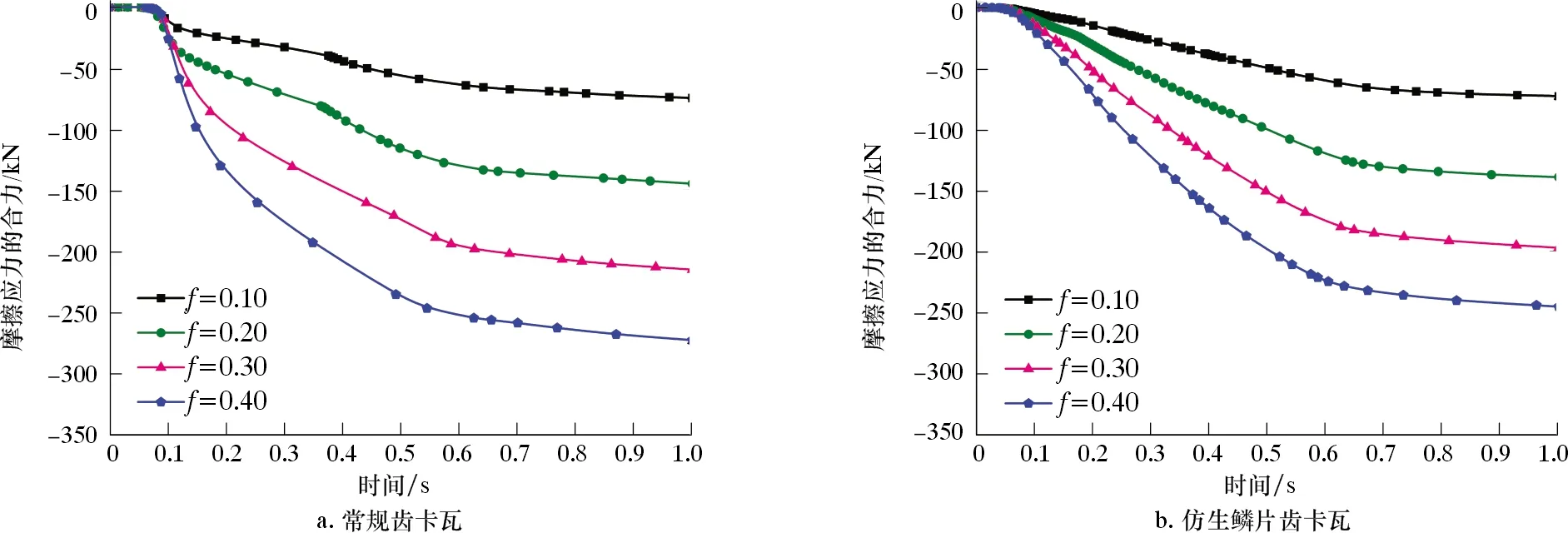
图16 不同摩擦因数下卡瓦与套管摩擦应力的合力Fig.16 Resultant force of friction stress between slip and casing with different friction coefficients

图17 不同摩擦因数下卡瓦与套管的接触面积Fig.17 Contact area between slip and casing with different friction coefficients
由图15和图16可知:常规齿卡瓦与套管接触压力的合力、摩擦应力的合力都随时间的延长以近似抛物线的形式增大,增长曲线易出现波动;仿生鳞片齿卡瓦与套管接触压力的合力起初以近似线性趋势快速增大,之后增大趋势处于平稳减缓状态,增长曲线平滑且稳定,摩擦应力的合力曲线也同样如此。从图17可以看出,在卡瓦牙齿与套管接触时,常规齿卡瓦与套管的接触面积起初以近指数形式迅速增大,然后迅速出现一段平稳过渡,之后接触面积呈不同的曲线形式增大,表现出明显的不稳定性;仿生鳞片齿卡瓦与套管的接触面积先以近似线性快速增大,之后增大趋势平稳减缓。
摩擦因数的增大对卡瓦与套管接触压力的合力和接触面积有一定的影响,且影响呈下降的趋势。显然,随着摩擦因数的增大,摩擦应力的合力也随之增大。综上所述,进一步说明了仿生鳞片齿卡瓦的稳定性优于常规齿卡瓦。
5 结 论
(1)建立了常规卡瓦牙和仿生鳞片卡瓦牙与弹性套管半空间体接触模型,推导出在弹性区域和塑性区域内卡瓦牙与套管相互作用力F和压入深度d的数学关系式。
(2)对比常规齿卡瓦的牙型结构参数,构建仿生鳞片齿卡瓦的牙型结构参数,建立了锥体-卡瓦-套管三维接触有限元模型,并利用有限元数值模拟对仿生鳞片齿卡瓦的牙型结构参数进行正交优化,得出仿生鳞片齿卡瓦的牙型最佳结构参数为:β′=90°、γ′=15°、R=5 mm、r=3 mm、α′=72°。优化后的仿生鳞片齿卡瓦比优化后的常规齿卡瓦在套管内表面产生的应力和牙痕深度要小,且应力减小了7.8%,牙痕深度了减小18.6%,证明了仿生鳞片齿卡瓦的微牙痕效果。
(3)通过改变卡瓦与套管接触面的摩擦因数,由数值模拟得出,对于常规齿卡瓦,摩擦因数的改变对套管的应力和变形的影响较大,而对于仿生鳞片齿卡瓦,摩擦因数的改变对套管的应力和变形的影响较小。对比常规齿卡瓦和仿生鳞片齿卡瓦分别咬合套管时,仿生鳞片齿卡瓦与套管接触压力的合力、摩擦应力的合力和接触面积与接触时间的关系曲线明显比常规齿卡瓦要更平滑且变化趋势更平稳。
