抽油机用盘式开关磁阻电机的电磁优化设计*
2022-07-12韩朋边敦新熊立新程建军夏强马宏昌鲁炳林
韩朋 边敦新 熊立新, 程建军 夏强 马宏昌 鲁炳林
(1.山东理工大学电气与电子工程学院 2.山东科汇电力自动化股份有限公司)
0 引 言
游梁式抽油机的胶带传动系统在工作中极易出现问题,如打滑、丢转、降低传动效率和减速器受力不均等[1]。为了解决这些问题,采用盘式电机主轴与减速器直接相连的半直驱方式。盘式电机则成为解决这些问题的核心部件。目前,国内已有盘式永磁同步电机应用于游梁式抽油机的实例[2],但是永磁同步电机存在成本高及永磁体不可逆退磁等问题,而且永磁体退磁极易导致电机效率降低,严重时会导致不能平稳启动抽油机。而开关磁阻电机(Switched Reluctance Motor,SRM)与之相比,内部没有永磁体,且具有成本低、结构简单可靠、转速范围宽、运行效率高、启动转矩大且电流小、可频繁启停以及过载能力强等诸多优点。传统的开关磁阻电机研究已经比较成熟,且成功应用于众多领域,如纺织、锻造、液压、油田和牵引机车等领域,特别是在抽油机上的应用,开关磁阻电机相比其他类型的电机具有节能的优势,且抽油机工作特性与电机合理匹配密不可分[3-4]。目前对盘式开关磁阻电机的研究大多都停留在试验研究阶段,随着产业的发展,对盘式开关磁阻电机的需求日益广泛,特别是其在抽油机中的应用更为迫切,需要结合产业化应用需求开展研究。
盘式SRM分为径向磁通和轴向磁通两类。径向磁通开关磁阻电机(Radial-Flux Switched Reluctance Motor,RFSRM)结构分为内转子和外转子两种结构。而轴向磁通开关磁阻电机(Axial-Flux Switched Reluctance Motor, AFSRM)结构各式各样,依据气隙的分布及数量,分为单层气隙、两层气隙和多层气隙的结构。两层气隙的AFSRM结构又可分为U形、C形、内侧转子和内侧定子等结构[5-9]。
RFSRM的磁场在轴向具有对称性,用简单的二维模型就能得到相对准确的结果。而AFSRM的轴向和径向磁场都不具有对称性,造成了在非对齐位置时,传统的解析法非常复杂且针对的定转子结构限制也很大[10],往往一换结构就需要重新推导。文献[11-13]中说明,准三维解析法在轴向磁通的永磁同步电机中得到了广泛的应用,而且对于轴向磁通的电机适用性强。文献[14]中,运用该方法计算了AFSRM在两个关键位置的磁化曲线,但是非对齐位置的边缘磁导部分造成了重复计算。对于这两种结构电机的对比研究中,文献[15]对8/6的两种电机在定子极的面积相等的情况下,对两电机的性能进行了对比,得出了AFSRM在转矩上比RFSRM更有优势的结论。文献[16-17]研究说明对于转矩的改进方面,更倾向于AFSRM。目前的研究中,多是针对一个特定尺寸约束进行的研究。在实际应用中,尺寸约束存在一个范围。本文旨在研究尺寸约束范围内,电机两种结构是否都能满足性能要求,选取哪一种结构达到效益的最大化。
本文以内转子的RFSRM和内侧转子的AFSRM为研究对象,在额定功率和转速相同,轴向和径向尺寸都满足实际尺寸约束的情况下,对这两种结构的盘式SRM进行了主要尺寸及转矩公式推导,并结合转矩公式对转矩性能进行了比较分析。运用解析法对两种结构的电机磁化曲线进行了计算。在准三维解析法的基础上,应用直线开关磁阻电机的气息磁导求解方法计算了AFSRM在非对齐位置的磁化曲线;在对齐位置,采用了两极模型计算了磁化曲线。最后运用三维有限元数值分析法进行结构优化并制造样机。样机试验结果验证了理论和仿真分析结果的正确性。装机试验结果说明盘式开关磁阻电机在满足生产性能要求的同时可以达到节能的效果。
1 盘式开关磁阻电机的基本结构
RFSRM和AFSRM的机械结构如图1所示。图1中电磁部分主要包括定子、转子和定子绕组。

1—定子;2—转子;3—定子绕组。图1 SRM的机械结构示意图 Fig.1 Mechanical structure of SRM
RFSRM的定转子磁极都采用平行齿。AFSRM的定子槽是平行槽,转子磁极采用辐射齿(转子齿的径向边延长线与旋转中心轴相交),如图2所示。图2b只给出了一侧的定子和全部转子极。
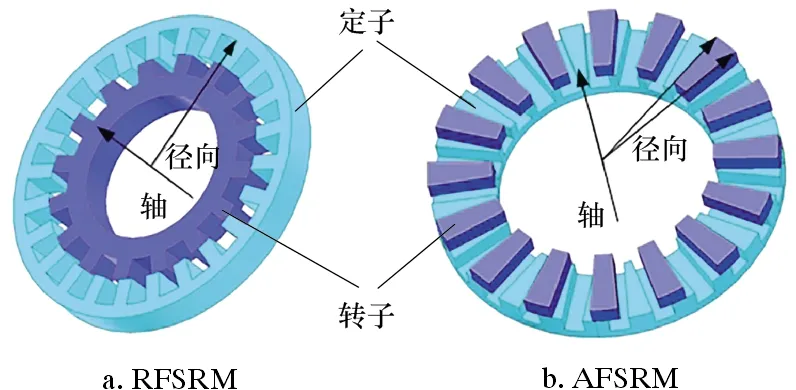
图2 SRM的电磁基本结构示意图Fig.2 Basic electromagnetic structure of SRM
采用这两种结构的原因如下:①有利于散热。由于盘式开关磁阻电机本身机壳设计时,为了使尺寸更小,散热部分相对薄弱。而这两种结构,定子线圈和铁芯都靠近机壳,有利于散热。②有利于机械结构设计。这两种结构的定子都是固定在机壳或端盖上,安装具有优势。
2 电机两种结构的理论分析
2.1 主要尺寸公式
2.1.1 RFSRM的主要尺寸
根据文献[18],RFSRM的尺寸满足下式:
(1)
式中:Da为转子铁芯外直径,m;lδ为铁芯的轴向长度,m;km为方波电流系数,取0.8;ki为峰值电流系数,取0.5;Bδ为电机磁负荷,T;A为电机电负荷,A/m;n为电机转速,r/min;Pem为电磁功率,W。
2.1.2 AFSRM的主要尺寸
AFSRM电磁功率的公式推导在文献[19]中有所介绍,但是根据此公式来确定电机的主要尺寸需要的参数较多。根据RFSRM的尺寸推导过程,对AFSRM的尺寸公式进行了推导,则有:
(2)
式中:Dout为定子铁芯外直径,m;Din为定子铁芯内直径,m;Dav为定子铁芯平均直径,m。
定子铁芯平均直径为:
Dav=(Dout+Din)/2
(3)
在转矩相同,电负荷和磁负荷的乘积相同情况下,由式(1)和式(2)可知:
(4)
通过式(1)和式(2)可以单独估算磁负荷和电负荷,计算出各自的尺寸;也可以在满足性能的RFSRM的尺寸上,在相同磁负荷及电负荷下,通过式(4)计算出AFSRM的尺寸。
2.2 直径比对转矩的影响
2.2.1 RFSRM的电磁转矩与直径比的关系
铁芯的轴向长度为:
lδ=L-π(Dout-2hsy)/Ns
(5)
式中:L为电机的轴向长度,m;Ns为一个定子盘的定子极数;hsy为定子轭的厚度,m。
定子轭的厚度计算式为:
hsy=0.325Doutkrβs
(6)
式中:βs为定子极外径处极弧,rad;kr为直径比。
直径比为:
kr=Din/Dout
(7)
由式(1)推导知,RFSRM的电磁转矩Tem为:
(8)
2.2.2 AFSRM的电磁转矩与直径比的关系
由式(2)推导知,AFSRM的电磁转矩Tem为:
(9)
电机轴向长度L一定时,在两种电机电负荷和磁负荷相同的情况下,电磁转矩是kr和Dout的函数。kr的取值范围为0~1。由式(8)和式(9)得出两种电机的电磁转矩与kr、Dout的关系,如图3所示。图3中Do_a和Do_r分别代表AFSRM和RFSRM的外直径。

图3 电磁转矩与直径比的关系图Fig.3 Relationship between electromagnetic torque and diameter ratio
由图3可以看出,kr的取值在0.25~0.40之间时,AFSRM对应的转矩较大。kr取值较小时,会出现3个问题:一是造成定子极外侧宽度大,而内侧宽度小,内侧力学强度小,容易造成机械损害; 二是造成定子极内侧部分磁场先于外侧饱和;三是考虑Din过小,平行槽的空间将限制绕组导线直径的选型,从而造成铜耗过大。综合以上考虑,AFSRM的直径比kr很多时候取不到转矩最大对应的值,所以在满足内径和力学性能要求的情况下,kr参考取值在0.6~0.7之间[20]。另外,随着kr的增大,RFSRM对应的转矩增大。考虑实际的定子轭和定子齿结构,kr参考取值应在0.4~0.7之间[18]。另外,在kr参考范围内,相同转矩时,AFSRM铁芯外直径可以比RFSRM要小。
2.3 纵横比对转矩的影响
2.3.1 RFSRM的电磁转矩与纵横比的关系
忽略电机外壳体尺寸,RFSRM的纵横比为λ,即轴向长度与电机整体外直径之比:
λ=L/Dout
(10)
将上式代入式(8)得:
(11)
2.3.2 AFSRM的电磁转矩与纵横比的关系
AFSRM的纵横比λ为:
λ=L/(Dout+2Lo_e)
(12)
式中:Lo_e为外侧端部绕组的径向长度,m。
其计算式为:
(13)
将式(12)和式(13)代入式(9)得:
(14)
在RFSRM和AFSRM的直径比kr分别取参考定值时,根据式(11)和式(14)得出转矩与λ、L的关系,如图4所示。图4中La和Lr分别代表AFSRM和RFSRM的轴向长度。
当L一定时,λ减小即外直径增大。由图4可以看出:随着λ减小,AFSRM对应转矩增大且增大速度较快;而RFSRM在纵横比λ大于0.2时,随着纵横比减小,对应转矩增大;在纵横比λ小于0.2时,随着纵横比减小,对应转矩减小。这是因为纵横比减小,RFSRM的端部绕组长度也在增大,导致铁芯轴向长度也在减小,由式(8)得到的转矩减小;当纵横比λ一定时,L越大,两种电机对应的转矩也越大;在L较小时,AFSRM比RFSRM在转矩上有优势。在L不是很苛刻的情况下,RFSRM的转矩可以满足电机性能要求。但是随着L的减小,RFSRM的转矩受到很大的影响,极易造成电机性能不能满足要求的情况。

图4 电磁转矩与纵横比的关系图Fig.4 Relationship between electromagnetic torque and aspect ratio
由图4还可以看出,在相同的轴向长度L时,可以得出两电机的转矩曲线有个交点。针对λ取值,分为3种情况:①λ取交点对应的值,两种结构的电机可以具有相同的尺寸和转矩;②λ取小于交点对应的值,则生产相同转矩的两种结构电机,AFSRM的整机外径要小于RFSRM的整机外径;③λ取大于交点对应的值,则生产相同转矩的两种结构的电机,RFSRM的整机外径要小于AFSRM的整机外径。
3 磁化曲线计算
3.1 RFSRM的磁化曲线计算
对于RFSRM,解析法研究相对成熟,也被大量实践所证实[18, 21]。采用磁路法研究时,对齐位置采用两极模型,从而计算出磁化曲线。非对齐位置可以近似认为铁芯磁导率无限大,磁动势集中在气隙部分,从而求得最小电感。
3.2 AFSRM的磁化曲线计算
对于AFSRM,以双定子盘(每个定子盘极数为24,转子极数为16)的三相开关磁阻电机为例。
AFSRM利用准三维解析法,将轴向磁通的电机沿径向分割成厚度均匀的各层,将各层单独分析,运用近似方法将各层展开为直线开关磁阻电机,分析步骤如图5所示,然后应用磁路法求气隙磁导。
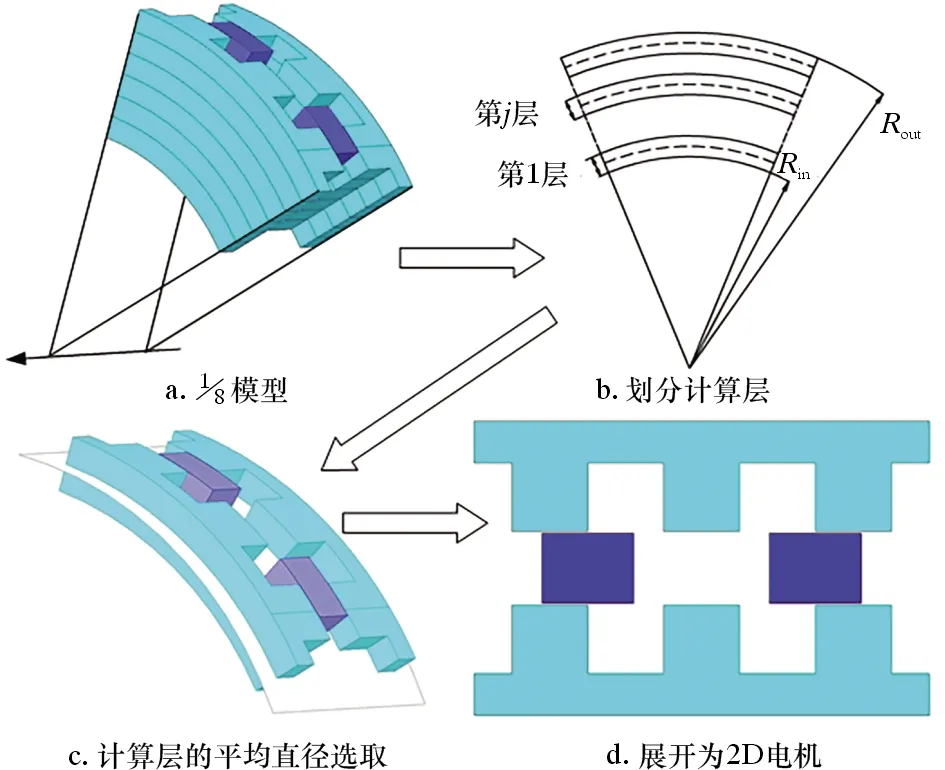
图5 AFSRM分析步骤示意图 Fig.5 AFSRM analysis steps
第j层的等效计算直径可以表示为:
(15)
式中:Ls为定子极径向长度,m;N为计算层数。
Ls=(Dout-Din)/2
(16)
i=2j-1
(17)
式中:j为第j个计算层,取值为1,2,……,N。
计算层中,第j层的计算参数可表示为:
ds=Douttan(βs/2)
(18)
aj=πDj/Ns-ds
(19)
βr_j=βr
(20)
bj=βr_jDj/2
(21)
dj=(cj-aj)/2
(22)
(23)
式中:βr_j为转子极弧,rad;aj为定子极宽,m;bj为转子极宽,m;cj为转子极间距,m;ds为定子槽宽,m;Ns为定子极数;βr_j为转子极外径处极弧,rad;βr为转子极弧,rad。
3.2.1 非对齐位置电机的磁化曲线计算
对每一个计算层直接应用直线开关磁阻电机的二维模型[22- 23],运用修正的直线开关磁阻电机的气息磁导求解结论,即可快速地求出各计算层的气隙磁导。在非对齐位置,铁芯内部平均磁密很小,可以近似认为铁芯磁导率无限大,磁动势集中在气隙部分。在计算每一个计算层的气隙磁导时,考虑如下假设,磁力线在气隙中走简单曲线,如直线或圆弧线等,则气隙中共有5种不同的磁通路径,分别表示为1~5共5个区域,如图6所示。
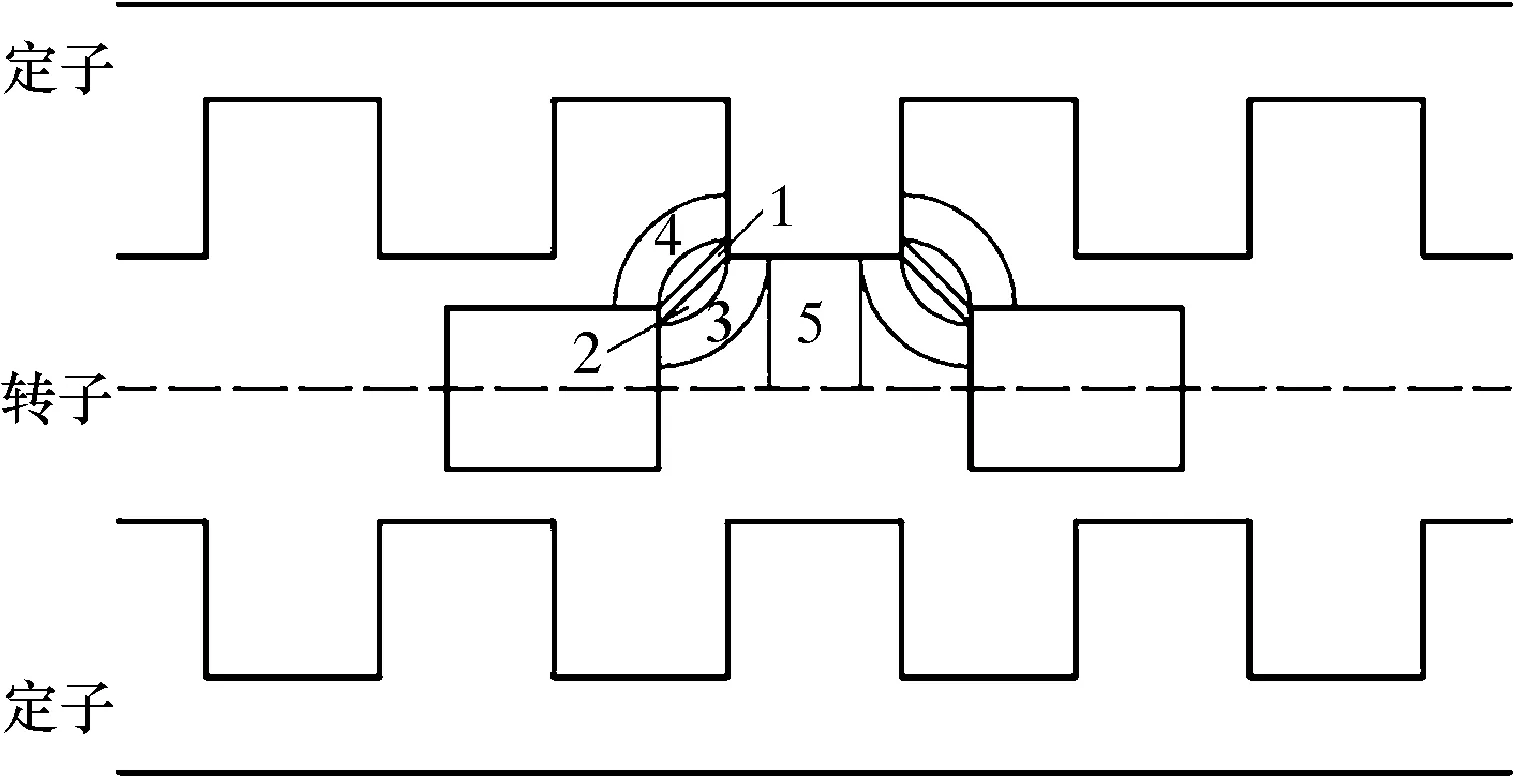
图6 AFSRM非对齐位置的计算层展开图Fig.6 Expansion diagram of the calculation layer in the unaligned position of AFSRM
图6中虚线对应的磁矢位A相等,由对称性可以只针对模型的上半部分求解,从而得出整个的气隙磁导。第j层的5个区域的气隙磁导分别为:
(24)
P2_j=0.134μ0Ls/N
(25)
(26)
(27)
(28)
式中:htr为转子极高度,m;g为第一气隙长度,m;μ0为真空中的磁导率。
计算层j上,对应的非对齐位置的气隙磁导为:
Pu_j=2P1_j+4P2_j+2P3_j+2P4_j+P5_j
(29)
对应一个定子极位置的气隙磁导为:
(30)
非对齐位置的最小电感为:
(31)
式中:Nph为相绕组匝数。
3.2.2 对齐位置电机的磁化曲线计算
忽略漏磁和磁分流,假设磁通均匀经过励磁的定子极、定子轭、转子极而闭合,可简化为两极模型。对于一个电周期的磁路,AFSRM对齐位置的计算层展开图如图7所示。一个磁网孔的总磁动势为:
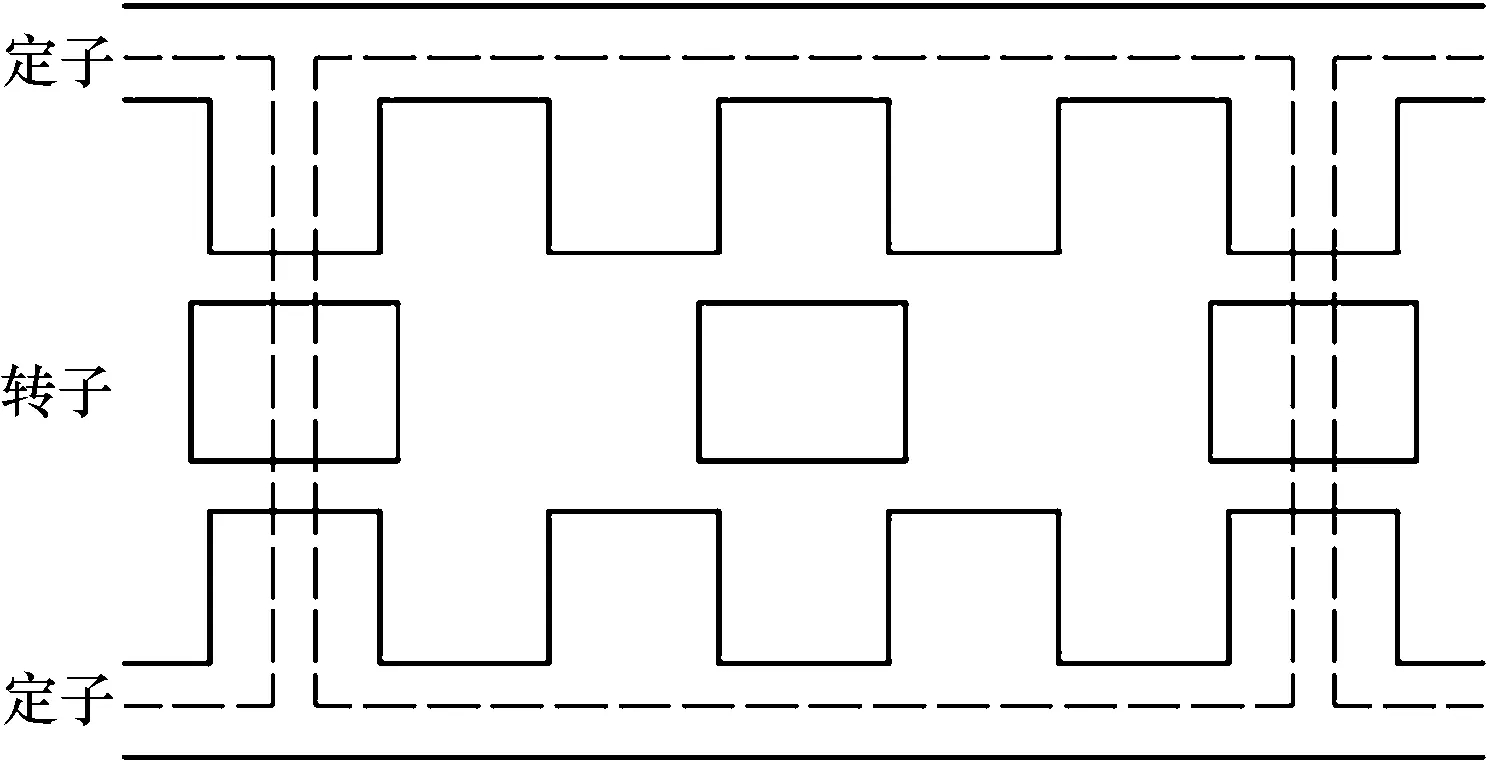
图7 AFSRM对齐位置的计算层展开图Fig.7 Expansion diagram of the calculation layer in the aligned position of AFSRM
(32)
式中:hts为定子极长度,m;lcs为磁通定子轭的路径平均长度,m;Hts、Htr、Hg、Hcs分别为定子极、转子极、气隙、定子轭对应的磁场强度,A/m。
根据磁路原理,对于不同的磁通密度,可以得出对应磁链与电流的关系,即磁化曲线。
4 有限元建模与结构优化
上述理论分析和计算方法对于RFSRM和AFSRM这两种结构盘式开关磁阻电机具有通用性,为了验证由此进行电磁设计的可行性,重新优化设计了RFSRM和AFSRM磁阻电机。具体指标要求如下:额定功率30 kW、额定电压514 V、额定转速300 r/min,并且轴向尺寸不大于220 mm,外直径不大于920 mm。
采用三相24/16结构,并对电机的结构参数(如定转子极高、定转子轭高和定转子极弧)进行优化,最终确定相关的结构尺寸及绕组参数如表1所示。

表1 24/16电机的设计参数Table 1 Design parameters of 24/16 motor
通过三维有限元建模仿真,得到RFSRM和AFSRM的两个关键位置的磁化曲线、相电流的波形图及瞬时转矩,分别如图8、图9和图10所示。图8a通过解析法和有限元法的比较,说明了应用改进的准三维解析法分析AFSRM的可行性。

图8 两个关键位置的磁化曲线Fig.8 Magnetization curves of two key positions

图9 相电流仿真波形图Fig.9 Phase current simulation waveform
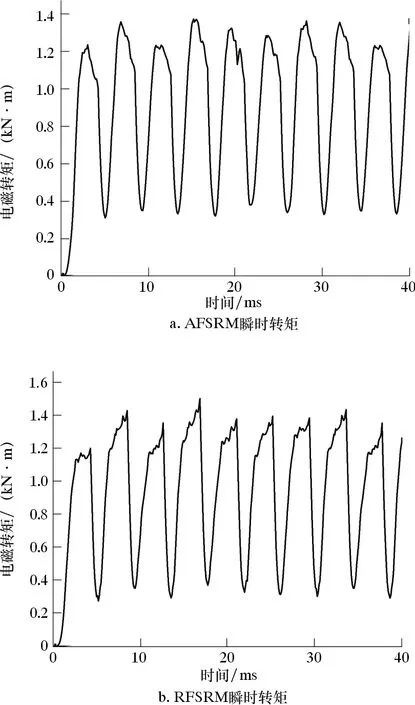
图10 瞬时转矩仿真波形图Fig.10 Instantaneous torque simulation waveform
另外,分别对RFSRM和AFSRM的转子极结构进行了优化。RFSRM优化参数如图11所示。图11中α1、α2为突出和凹进部分的圆弧角;h1、h2为突出和凹进部分的厚度。取α1=α2,h1=h2,并分别取不同的数值,如表2所示,并进行有限元建模仿真。

图11 RFSRM转子极结构优化Fig.11 Optimization of RFSRM rotor pole structure

表2 RFSRM转子极优化参数Table 2 Optimization parameters of RFSRM rotor pole
仿真结果中,取α1=α2=0.5°,h1=h2=1g时,电磁转矩最大。与转子极优化前对比,平均转矩提升了6.7%,转矩脉动减小了4.5%。
AFSRM的转子极是分立的,需要做成中间突起的样式才能安装,如图12所示。图12中l1为突起部分的长度,l2为突起部分的厚度,l1、l2分别取不同的数值,如表3所示,并进行有限元建模仿真。
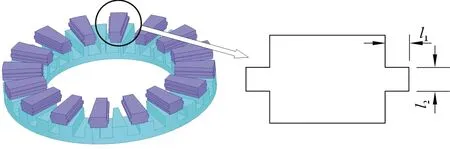
图12 AFSRM转子极结构优化Fig.12 Optimization of AFSRM rotor pole structure

表3 AFSRM转子极优化参数mmTable 3 Optimization parameters of AFSRM rotor pole mm
仿真结果中,取l1=5.00 mm,l2=8.50 mm时,电磁转矩最大。与转子极优化前对比,平均转矩提升了5.2%,转矩脉动减小了8.3%。仿真结果说明,在轴向尺寸为220 mm时,两种结构的电机都满足性能要求,而且AFSRM比RFSRM的外直径要小。
5 试验验证
为了检验前文的理论和仿真结果,基于加工成本、结构复杂度及装配难度考虑,由计算的电机参数选择RFSRM这种结构完成样机的制造。搭建电机试验平台,如图13所示。

图13 电机试验平台Fig.13 Motor experiment platform
该样机的启动性能如图14所示。在控制器的峰值电流下,启动转矩约为额定转矩的2.3倍。电机满载时,系统效率随转速的变化曲线如图15所示。
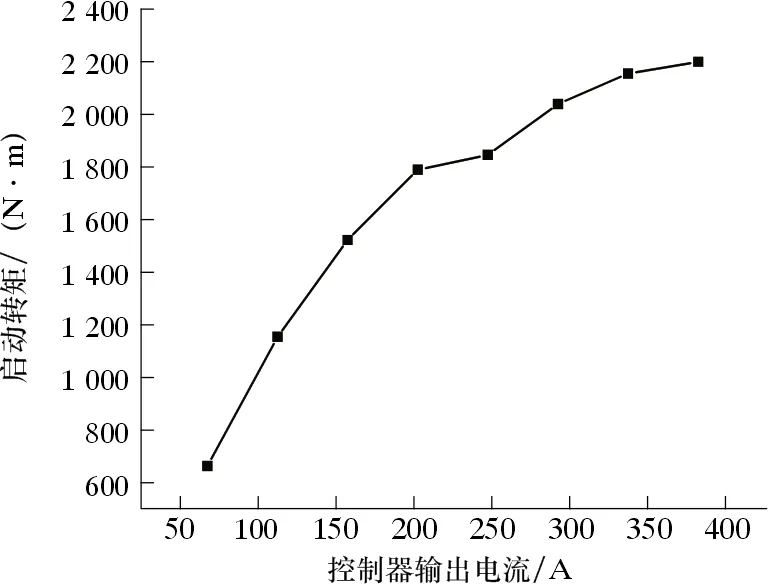
图14 最大启动转矩Fig.14 Maximum starting torque

图15 系统效率随转速的变化曲线Fig.15 Change curve of system efficiency with rotation speed
经试验测试,样机的试验参数如表4所示。
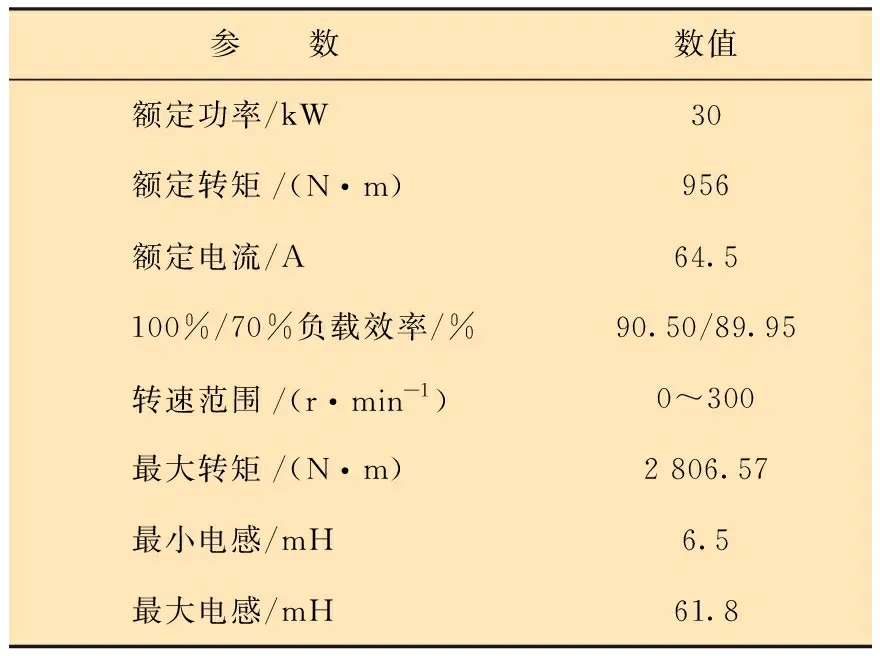
表4 样机试验参数Table 4 Prototype experiment parameters
试验结果说明,在满足尺寸范围要求下,选择径向磁通开关磁阻电机这种结构制造样机可以完成启动和运行。通过装机试验,并取24 h电表计量的数据与不同类型电机在冲程、冲次和日产量几乎相同的情况下做节能对比,结果如表5所示。

表5 抽油机电机节能对比Table 5 Comparison of energy saving of pumping unit motors
开关磁阻电机相较于三相异步电机有功节电率达到27.4%,相较于交流永磁伺服电机有功节电率达到7.9%,说明开关磁阻电机与抽油机工作特性是匹配的,样机满足生产要求。
6 结 论
(1)在性能和尺寸满足的范围内,基于加工成本、结构复杂度及装配难度考虑,应优先选径向磁通电机结构。当轴向尺寸和外直径要求比较苛刻的情况下,选择轴向磁通的电机结构则更具优势。
(2)针对AFSRM的磁化曲线,在非对齐位置时,修改的直线开关磁阻电机气隙磁导求解方法的精度较高,能够满足电机初期的设计要求。
