地震下大跨双塔单侧混合梁斜拉桥非对称黏滞阻尼器设置参数分析

邓育林 易 磊

(武汉理工大学交通与物流工程学院 武汉 430063)

0 引 言

随着对地震作用研究的不断深入，许多大跨的斜拉桥都采取了减隔震设计进行地震灾害的预防．其中黏滞阻尼器因其结构简单、适用性广泛、减震效果好，以及使用寿命长等优点而被广泛的应用在桥梁减震设计中[1]．黏滞阻尼器对结构的减震能力与其设置参数密切相关，不同的桥梁阻尼器参数设置一般都有差别，因此需要进行参数优化设计．

目前国内外有许多学者对黏滞阻尼器参数优化方面进行了研究．Jennifer等[2]分析了黏滞阻尼器尺寸、阻尼器内部尺寸及外部支承对斜拉索减震器减震效率的影响．Xu等[3]提出了一种利于确定阻尼器参数的简化方法．叶爱君等[4]通过Sap2000探讨了附加阻尼器对超大跨双塔斜拉桥的减震影响．巫生平等[5]通过对苏通大桥的分析，明确了斜拉索设置阻尼器的减震影响．王波等[6]通过对边跨有桥台的斜拉桥的研究，发现在桥台处设置阻尼器减震效率高．张文学等[7]探讨了斜拉桥桥面高不同时阻尼器减震效率问题．陈百奔等[8]通过ANSYS软件进行了斜拉桥阻尼器设置参数优化组合分析．徐秀丽等[9]探讨了超大跨双塔对称斜拉桥设置了横向阻尼器时的参数分析．韩万水等[10]采用Maxwell阻尼模型模拟并分析了黏滞阻尼器的滞回耗能特性及其影响．徐艳等[11]提出了考虑附加黏滞阻尼器的漂浮体系斜拉桥三质点简化动力模型并通过分析表明，简化模型有利于更合理和准确地设计阻尼器参数．

尽管目前有许多学者对斜拉桥黏滞阻尼器进行了参数分析和优化，但基本都是对双塔斜拉桥塔梁连接处设置对称的阻尼器参数进行的分析，而少有对双塔斜拉桥塔梁连接处设置非对称的阻尼器参数进行分析．文中以一座大跨双塔单侧混合梁斜拉桥为例，基于midas/Civil程序建立了桥梁的空间有限元模型，采用非线性时程方法分析了纵向黏滞阻尼器不同参数组合下地震动响应，探讨阻尼器参数对称设置与不对称设置塔顶位移、梁端位移和塔底内力响应的减震效果．

1 非线性黏滞阻尼器力学模型

黏滞阻尼器作为一种高效的耗能装置，主要是为结构提供阻尼力从而消耗结构能量，而不会改变结构的振动特性．阻尼器阻尼力与速度为

F=CVξ

(1)

式中：F为阻尼力；C为阻尼系数；V为相对运动速度；ξ为速度指数，抗震中常用范围在0.2～1.0．ξ=1时为线性阻尼器，ξ≠1时为非线性阻尼器．

在midas/Civil程序中液体黏滞阻尼器一般利用Maxwell模型[12]来模拟，见图1，模型由线性弹簧和阻尼器串联而成．Maxwell 模型力-变形关系式为

图1 Maxwell模型

(2)

式中：dd为阻尼器的变形量；db为弹簧的变形量；v0为参考速度，一般取值为1；sign( ) 为符号函数；kb为弹簧刚度．

2 工程概况及有限元模型

2.1 工程概况

文中结合工程实例，以双塔单侧混合梁斜拉桥为例，桥梁的桥跨布置图见图2，其跨径布置为75 m+75 m+75 m+820 m+300 m+100 m．北边跨为长251.5 m的混凝土主梁；中跨和南边跨为钢主梁，总长1 193.5 m．南塔及北塔总高232 m．在桥塔横梁、各桥墩处设置球型钢支座，纵向黏滞阻尼器设置在了塔梁连接处，桥梁的支撑体系简图见图3．全桥共4×26对拉索．

图2 斜拉桥立面布置图(未注单位的尺寸单位：cm)

图3 支撑体系布置图

2.2 有限元模型

大跨斜拉桥动力特性及地震响应空间效应明显，因此，研究其抗震性能应采用空间结构的有限单元方法．用midas/Civil软件建立有限元模型见图4．模型中坐标轴x、y和z方向分别表示顺桥向、横桥向和竖向．

图4 有限元模型

模型采用梁单元模拟主梁、主塔和桥墩，主梁采用单梁模型，刚度为梁的实际刚度，将桥面所有质量计入主梁，并考虑扭转质量惯矩的影响．斜拉索采用空间桁架单元，采用Ernst有效弹性模量法[13]考虑拉索垂度效应，以最终成桥索力值进行索力输入．采用刚臂单元来连接斜拉索与主梁，球型支座边界采用弹性连接．黏滞阻尼器用Maxwell模型模拟．用集中质量来模拟承台并且在承台节点处采用六弹簧考虑桩-土影响．考虑主和引桥之间地震作用的耦联效应，在南北两侧的一联引桥也一起建模．

3 地震动输入

在进行桥梁结构非线性时程地震反应分析时，根据桥梁自振特性和场地效应，选取七条人工地震波．地震动加速度时程图见图5，图6为各人工波反应谱以及设计反应谱．为了分析纵向阻尼器对桥梁结构抗震性能的影响，七条人工地震波采取纵向的输入方式，计算结果取七条人工波的平均值．

图5 地震动加速度时程

图6 地震动反应谱

4 阻尼器参数对称设置分析

4.1 阻尼器参数设置

北塔和南塔塔梁连接处分别设置了四个黏滞阻尼器，阻尼器参数对称设置即是讨论北塔处和南塔处的参数设置相同．对控制阻尼器的两个主要参数速度指数ξ和阻尼系数C分别进行组合分析，取ξ=0.2、0.3、0.4、0.5、0.6、0.7、0.8共七个值；取C=500、1 000、1 500、2 000、2 500、3 000、3 500、4 000、5 000、6 000和7 000共11个值，单位均为kN/(m/s)ξ，共计算77 工况．

4.2 位移效应

图7为主梁南、北端的纵向位移比．位移比表示设置阻尼器的位移最大值与未设置阻尼器位移最大的比值，可以清楚地表示设置阻尼器后对位移减震效果，同时可以代表位移变化规律，后文各内力比与位移比表示方式相同不再赘述．由图7可知：ξ一定时，C增大，主梁位移减小，且随C的不断增大，主梁位移变化逐渐平缓；C一定时，ξ越小，主梁位移的减幅越大；为了减小主梁纵向位移，可取较小的速度指数ξ，同时在一定范围内增大阻尼系数C．

图7 主梁南、北端纵向位移比

对比两端主梁位移情况可知，当两塔主梁连接处阻尼器参数对称设置时，主梁北端纵向位移减小幅值明显小于主梁南端纵向位移幅值．

图8为南、北塔塔顶位移比．由图8可知：塔顶位移变化趋势与两端位移变化趋势相同，因此为了减小塔顶位移，阻尼器参数可与梁端位移参数取值一致．

图8 南、北塔塔顶纵向位移比

对比南、北塔塔顶位移情况可知，当两塔主梁连接处阻尼器参数对称设置时，南塔和北塔位移减小幅值基本相同．

4.3 内力效应

由于主桥各辅助墩和过渡墩与主梁纵向无约束，设置阻尼器前后各墩底的弯矩和剪力无明显变化．因此在分析内力效应时，主要对南、北塔内力响应进行分析，见图9．

图9 南、北塔塔底剪力比

由图9可知：不同速度指数时塔底剪力先减后增，并且剪力最小值对应的C值是不同的，ξ越小，剪力比最小值对应的C值越小；C取较大值并且ξ较小值时，会增大塔底剪力响应；与位移减震效果相比而言，设置阻尼器对该桥塔底剪力减震影响很小．因此在对参数组合优化时，主要是避免因速度指数过小而阻尼系数过大导致剪力增大的不利情况．当两主塔塔梁连接处阻尼器参数对称设置时，南塔和北塔剪力变化规律有所不同；速度指数相同时，北塔剪力比最小值对应的阻尼系数值比南塔的小．

图10为南、北塔塔底弯矩比．由图10可知：设有阻尼器的情况下塔底弯矩比较小，表明阻尼器对塔底弯矩的减震效果明显；塔底弯矩先减后增，且不同ξ下，弯矩最小值对应的C值不同，ξ越小，弯矩比最小值对应的C越小；且不同速度指数下的拐点值大小相近，因此考虑阻尼器对塔底弯矩减震效果时，可取各拐点附近对应的速度指数和阻尼系数．

图10 南、北塔塔底弯矩比

对比南、北塔塔底弯矩情况可知，当两塔主梁连接处阻尼器参数对称设置时，同一速度指数下北塔塔底弯矩拐点对应的阻尼系数比南塔的大，如当ξ=0.3时北塔塔底弯矩比最小值对应的阻尼系数C=2 000 kN/(m/s)ξ，南塔的为C=1 000 kN/(m/s)ξ；因此在两塔阻尼器参数对称设置时无法同时使得南、北塔塔底弯矩取最小，若要使南北塔塔底弯矩减小幅度同时达最优，还需进一步对两处阻尼器参数进行非对称组合分析．

4.4 黏滞阻尼器阻尼力

因阻尼器设置位置时是在塔梁连接处，地震作用下阻尼器产生的阻尼力会传到主梁，从而对主梁局部会产生较为不利的影响．图11为阻尼力变化情况．由图11可知：阻尼力与阻尼系数呈正相关，与速度指数呈负相关，且阻尼器系数对阻尼力的影响显著．因此，对阻尼器参数进行优化组合时，为了避免阻尼力过大对主梁造成危害，应首要选比较小的阻尼系数C．

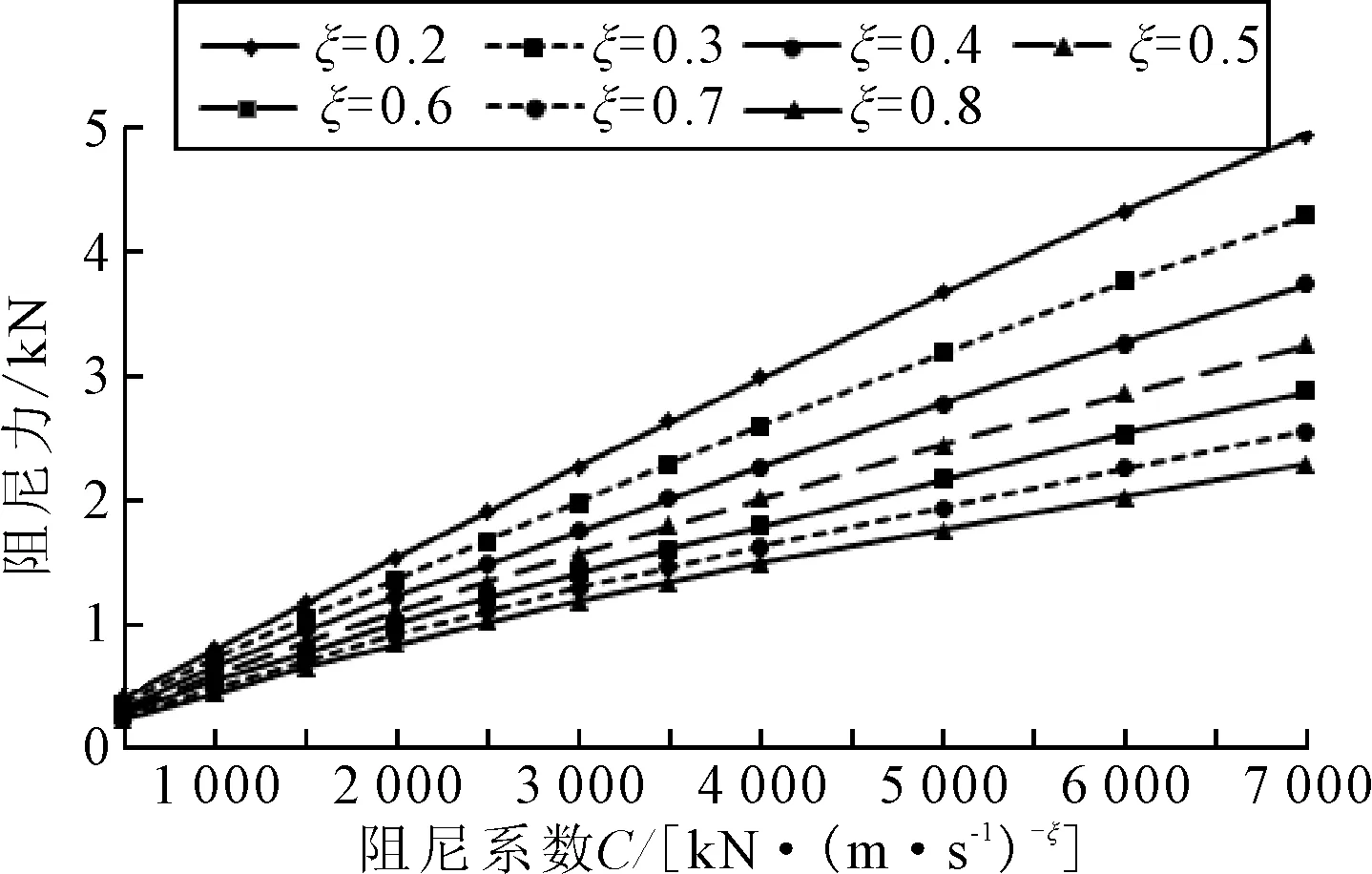
图11 阻尼力

综合考虑黏滞阻尼器参数对结构位移、内力和阻尼器阻尼力的影响，在两塔主梁连接处阻尼器参数对称设置时，减震效果较好的参数组合取值为ξ=0.3，C=2 000 kN/(m/s)0.3．南、北塔处阻尼力峰值最大为1 356.4 kN．

5 阻尼器参数非对称设置分析

由于该桥为非对称布置，以上分析表明阻尼器参数对称布置时表现出来主梁两端的位移差别以及北塔与南塔内力变化的不一致，有必要对阻尼器参数进行非对称组合分析．阻尼器参数组合分析设置工况如下：为与上文得出较优的阻尼参数组合形成对照，南、北两侧阻尼器速度指数均取ξ=0.3，北侧阻尼系数取Cn=1 000、1 500、2 000、2 500、3 000和3 500 kN/(m/s)ξ共六个值；南侧阻尼系数取Cs=500、1 000、1 500、2 000、2 500和3 000 kN/(m/s)ξ共六个值，共计36个工况．

由以上分析表明阻尼器参数设置主要对位移和弯矩影响较大，因此在进行阻尼器参数不对称设置分析时主要讨论主梁位移及塔底弯矩的影响．

图12为各工况下主梁北端和南端的位移比．由图12可知：阻尼系数Cs和Cn越大主梁纵向位移越小，即位移减震效果更好；但北塔处的Cn大到一定的值时，随南塔处Cs增加主梁位移减幅不明显．因此为了提升对主梁位移减震效果，可在一定程度尽量增大南、北两处阻尼系数值．

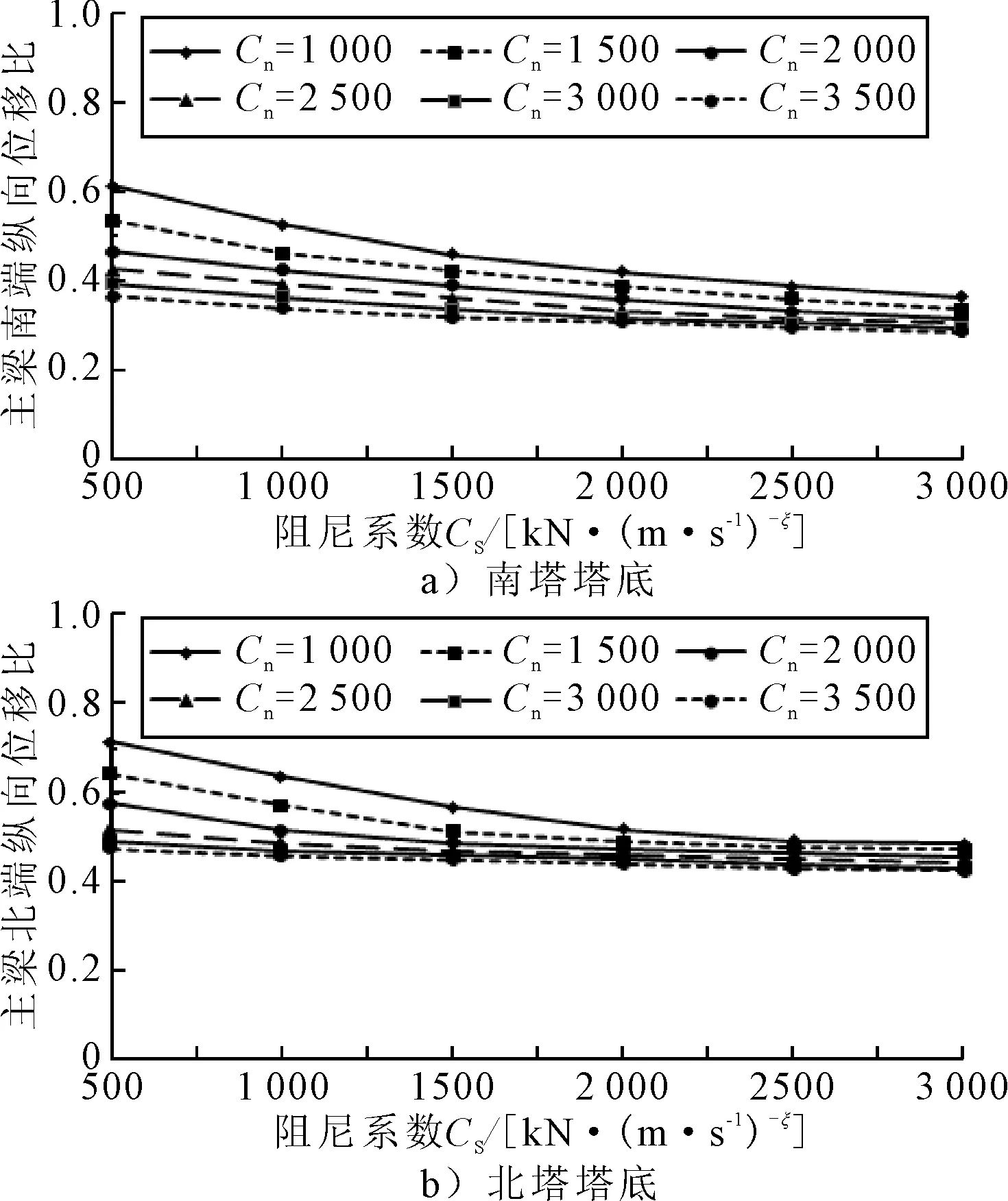
图12 主梁南、北端纵向位移比

图13为工况下南、北塔的塔底弯矩比变化情况．由图13可知：当一侧阻尼系数一定时，随着另一侧阻尼系数增大，北塔的塔底弯矩先减后增；其中当北塔阻尼系数Cn取值较大值，南塔阻尼系数Cs取较小值，北塔塔底弯矩减震效果较好．对于南塔塔底弯矩，当北塔处阻尼系数Cn取1 000 kN/(m/s)ξ时，随Cs的增大其弯矩值先减小后增大；当Cn取1 500～3 000 kN/(m/s)ξ时，随Cs的增大南塔塔底弯矩一直增大，且Cs较小时，北塔阻尼系数Cn对南塔塔底弯矩减震效果影响较小．因此为提高南塔弯矩减震效果，南塔处阻尼器系数应取较小值．

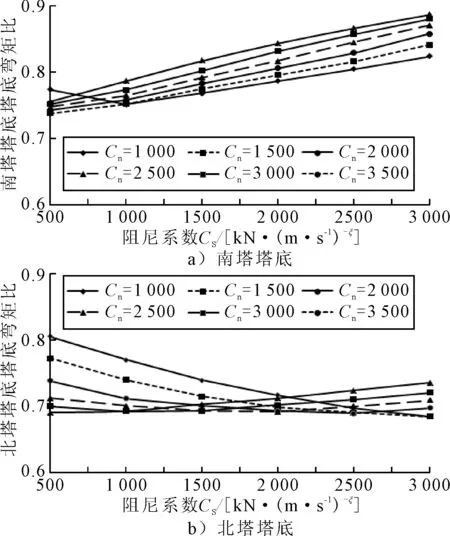
图13 南、北塔塔底弯矩比

在同时考虑对南、北塔塔底弯矩减震影响时，尽量增大北塔阻尼系数，适当减小南塔阻尼系数可使减震结果达到更优．

综合考虑黏滞阻尼器参数对结构位移、内力和阻尼器阻尼力的影响，在两塔主梁连接处阻尼器参数对称设置时，减震效果较好的参数组合取值为北塔处ξ=0.3，Cn=3 000 kN/(m/s)0.3，南塔处ξ=0.3，Cs=500 kN/(m/s)0.3．北塔、南塔处阻尼力峰值最大分别为2 015.5 kN、348.8 kN．

6 减震效果

对于地震响应的减震效果通常用减震率来表示，减震率表示为设置阻尼器前后地震响应差值与未设阻尼器地震响应的比值，减震率越大表明减震效果越好．

图14为对称和非对称设置阻尼器参数最优组合时的减震率．由图14可知：参数对称设置与非对称设置位移减震率大小相近，对称设置的位移减震率比非对称设置的略大．两种情况下剪力的减震率很小，弯矩的减震率比较大；非对称设置情况下南塔塔底弯矩减震率有明显提升且保持北塔塔底弯矩减震率基本不变，表明非对称设置情况下南、北塔塔底弯矩达到更优的减震效果．

图14 位移与内力减震效果

图15为No.1地震波下设置阻尼器前后弯矩和位移的时程图．由图15可知：在未设阻尼器的时，结构位移和弯矩响应峰值大，对称设置和非对称设置了阻尼器后，位移和弯矩响应峰值明显小了许多．设有阻尼器时，主梁梁端的位移值控制在了比较小的范围内，可降低主梁与引桥发生碰撞的几率．

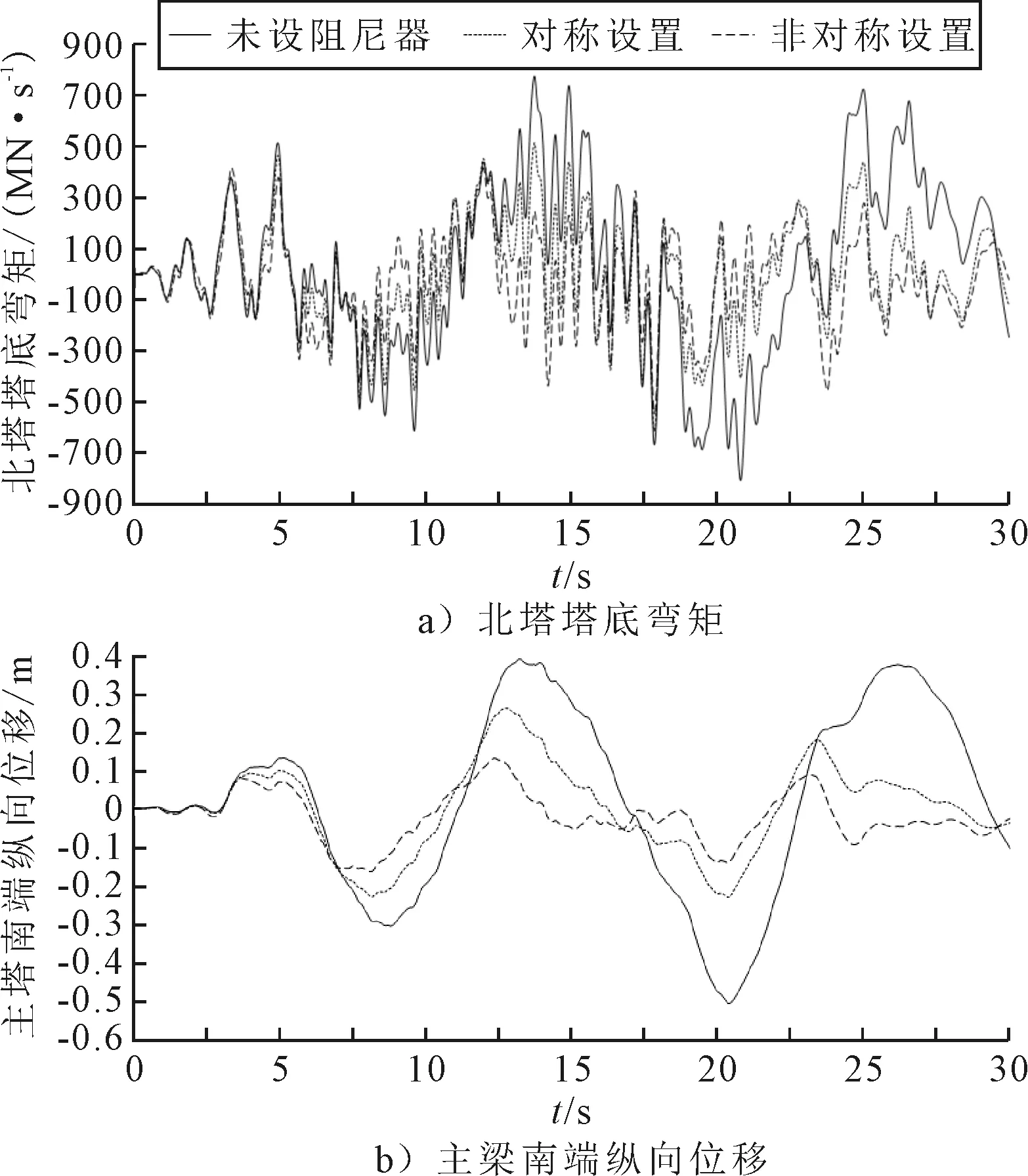
图15 时程响应

7 结 论

1) 大跨半漂浮体系的斜拉桥在塔梁连接处设置纵向黏滞阻尼器可以有效的降低桥塔、主梁关键位置的位移，从而降低主梁与引桥发生碰撞的概率．

2) 合理优化后的阻尼器参数组合可兼顾对位移及内力的减震，使其同时达到对结构最为有利的减震效果．

3) 大跨双塔单侧混合梁斜拉桥在阻尼器参数非对称设置时，在混合梁一侧的阻尼系数取较大值，钢主梁一侧阻尼系数取较小值，对塔底内力减震效果更优．

4) 阻尼器参数对称设置和非对称设置时最优参数组合都可以有效提高位移和弯矩的减震率，且两种参数组合下各响应的减震率相差不大．不同的是阻尼器参数对称设置时，两塔处阻尼器都相同，方便实际工程中阻尼器的制作和安装；而阻尼器参数非对称设置时，因钢主梁一侧阻尼力较小，可以减小阻尼力对钢主梁的影响．黏滞阻尼器参数非对称设置为该类桥提供新的阻尼器布置方案供参考．