拉索失效和主梁损伤斜拉桥静力性能退化模型试验

马亚飞，彭安银，王磊，张建仁

(长沙理工大学土木工程学院，湖南长沙，410114)

在不利环境和外界荷载等因素影响下，服役斜拉桥一些构件会发生不同程度损伤，如拉索腐蚀、主梁开裂等。对斜拉桥结构进行安全评定时，若对损伤考虑不足则将产生误判，存在重大安全隐患[1]，因此，有必要对斜拉桥在损伤工况下的静力性能退化规律进行研究。模型试验是研究复杂桥梁结构性能的重要手段之一。节段模型具有节省成本、可操作性强等优点，被广泛采用。SHAO等[2]通过1:6 的节段模型试验，验证了竖琴形单跨斜拉桥的主梁稳定性和全桥稳定性。HUANG 等[3]基于相似比理论，通过节段模型给出了桥梁的关键设计参数。上述缩尺模型试验主要用于检验正常施工或运营条件下斜拉桥全桥或节段的静动力学特性，对设计理论参数和计算结果进行验证，但涉及斜拉桥损伤工况研究较少。一些研究者对拉索和桥塔损伤后的结构性能进行了研究，如：ZHANG 等[4]通过现场实测和数值仿真方法研究了多根拉索断裂后混凝土主梁裂纹的形成和分布规律；HOANG 等[5]研究了斜拉索在侧向力作用下突然断索的振动特性，提出了拉索抗冲击力系数建议值；NAZARIAN等[6]结合模型试验给出了拉索张力损失和主梁应变分布的关系；YI等[7]对倒Y型桥塔腿进行振动台试验，建立了考虑斜塔腿开裂后扭转刚度降低的数值模型，揭示了斜塔腿下部混凝土开裂的原因；WANG等[8]研究了大跨度斜拉桥钢筋混凝土桥塔在横向地震波作用下的破坏机理与延性；KAO等[9-10]在模型试验基础上采用有限元方法研究了断索对其他拉索索力、斜拉桥内力、位移和极限承载力的影响；WOLFF 等[11-12]通过非线性动力分析研究了拉索断裂下的动力响应和动力放大系数，并提出了相应的理论模型；ZHOU等[13]对拉索损伤下大跨斜拉桥可靠性评估提出了建议。上述研究多针对拉索损伤工况，而对斜拉桥在服役期间存在的主梁梁体开裂等损伤工况考虑较少。主梁损伤直接影响斜拉桥主梁截面刚度，其引起的结构性能变化较拉索断裂存在区别。GUO 等[14]研究了斜拉桥钢箱梁横隔板开裂后的裂缝形态、位置和破坏机理，但未考虑主梁损伤对斜拉桥力学性能的影响。刘国坤等[15]开展了混凝土斜拉桥节段模型试验的强扭试验，研究了主梁受损后的抗扭承载力和弯曲性能。张国刚等[16]分析了考虑主梁损伤状态下模型桥和原型桥的静动力特性。HASHEMI 等[17-18]研究了爆炸荷载引起的主梁损伤对斜拉桥全桥结构响应的影响。然而，上述研究未全面考虑不同断索和主梁损伤工况对斜拉桥结构静力性能退化规律的影响。

本文以合江长江二桥为工程背景，考虑全桥拉索断裂和主梁损伤工况，设计斜拉桥节段模型，开展不同损伤工况下的斜拉桥模型试验，揭示断索和主梁损伤对拉索索力、主梁应力和挠度分布规律的影响，研究成果可为服役斜拉桥的性能评估和损伤识别提供参考。

1 模型试验设计

1.1 工程背景

沪渝高速合江长江二桥为1 座跨径为(210+420+210)m的刚构体系双塔预应力混凝土斜拉桥。斜拉索采用双索面、密索、对称扇形布置，主梁为预应力混凝土纵肋式连续梁，主梁节段长度为6.000 m，桥面宽30.000 m，标准截面梁高3.000 m。索塔为H 型塔，高146.300 m。拉索采用双索面布置，每个索塔设置34 对斜拉索。桥型布置如图1所示，主梁和拉索材料属性如表1所示。

图1 合江二桥总体布置图Fig.1 Layout of the second Hejiang Bridge

表1 主梁和斜拉索材料属性Table 1 Material properties of the main girder and stay cables

1.2 模型桥设计与验证

选取左塔墩梁固结处至辅助墩137.000 m 梁段进行模型设计，几何相似比λ=1/40。根据相似比理论换算，主梁采用厚度为6.000 mm 的钢板焊接，斜拉索采用直径为3.000 mm 的钢丝绳。由于本模型采用多相材质结构，故采用刚度相似法确定相关模型的尺寸，即将轴向刚度(EA)、抗弯刚度(EI)和截面抗弯抵抗矩(EW)作为复合物理量进行处理(其中，E为弹性模量，A为主梁横截面面积，I为主梁截面抗弯惯性矩，W为主梁横截面抗弯截面模量)，λE=6(λE为弹性模量相似比)，原型桥与模型桥相似对应关系如表2所示。

表2 模型桥中主要参数的相似比Table 2 Similarity ratio of main parameters in model bridge

模型桥主梁长为3.425 m，分段长为(1.175+1.200+1.050)m，梁宽为0.400 m，主梁截面采用边箱梁。在钢箱梁节段拼接位置的边箱梁内外侧各布置1块主梁连接钢板，钢箱梁节段与节段之间用连接钢板与M12 螺栓连接，形成钢主梁并保证主梁纵向连续性。纵桥向钢箱梁的连接如图2 所示。原型桥有22 对斜拉索，若按相似理论设计，拉索在主梁上的锚固间距仅为0.15 m，不便于加工制作。此外，斜拉索布置过密，索力变化不明显，不利于开展典型损伤下(如拉索断裂)的斜拉桥模型试验。将本模型桥斜拉索简化为8对，保留边墩和主塔处的拉索，中间拉索按相邻3根合为1根。模型桥布置如图3所示。

图2 钢箱梁纵向连接Fig.2 Longitudinal connection of steel box girder

图3 模型斜拉桥总体布置图Fig.3 Layouts of cable-stayed bridge model

利用MIDAS/CIVIL 建立原型桥和模型桥的空间有限元模型，如图4所示。主梁、墩塔均采用梁单元，斜拉索采用仅受拉索作用的单元。斜拉索与主梁采用刚性连接。原型桥的作用荷载按现行规范进行组合。模型桥的配重荷载为12.13 kN/m，按均布荷载增加，不考虑结构自重。虚拟荷载为25.00 kN/m，以考虑原型桥中二期恒载、温度和活载等作用，按均布荷载施加。模型桥的静力荷载工况为配重、斜拉索设计索力和虚拟荷载的组合，荷载均按恒载设计，荷载组合系数均为1。

图4 有限元分析模型Fig.4 Finite element model

经相似换算后模型桥竖向挠度和主梁弯矩与原型桥的对比结果如图5(a)和图5(b)所示。模型桥未调整前，其索力经相似换算后，与原型桥的索力对比结果如图5(c)所示。模型调整后，采用未知荷载系数法予以调索，保证关键截面的应力和挠度均保持在未调整前的值。表3所示为模型桥调整后的设计索力。由图5可知：模型桥与原型桥的位移分布基本相同。由于斜拉索数量减少，模型桥的内力出现波动，但其内力变化趋势与原型桥内力变化趋势基本一致，模型桥各内力的均值点均落在原型桥的内力曲线上。这表明模型桥的设计合理，能真实反映原型桥受力情况。

表3 调整后模型桥设计索力Table 3 Design cable force of model bridge after adjustment

图5 模型桥与原型桥的静力相似对比Fig.5 Comparison of static similarity analysis between model bridge and prototype bridge

1.3 试验加载及测点布置

理想模型所需材料密度不符合要求，在现实中难以直接采用，因此，模型设计中需采用配重方式进行等效。按相似比理论，需在主梁上按12.1 kN/m进行配重，合计配重4.2×104N。鉴于试验条件限制和试验目的不同，采用放宽密度相似比对模型桥进行配重[19-20]。主梁配重3.2 kN，采用32组10 kg砝码作为配重质量块。拉索和主塔不考虑配重。试验荷载为2.0 kN，采用40 组5 kg 砝码分为10 级进行加载。在正式加载前，采用10 组10 kg砝码进行预加载。

模型试验加载装置如图6所示。在斜拉索上设置索力测量和调整装置，索力测量装置由不锈钢薄铁片和电阻应变计组成，斜拉索索力采用花篮螺丝调整钢丝绳松紧状态获得。斜拉索和钢主梁通过半羊眼螺丝连接。在钢主梁上设置3个主梁损伤区域，损伤区域采用图3(c)所示截面形式，主梁其他区域采用图3(b)所示的截面形式。图3(c)中的底板和钢主梁螺接形成整体。对模型桥主塔进行简化，主塔采用钢板与反力墙螺接锚固模拟。斜拉索和主塔钢板采用带环螺丝连接。斜拉索的端部锚固采用钢丝绳夹头。桥墩采用角钢焊接，模拟竖向、横向及纵向的约束，塔墩梁固结处采用螺栓连接以模拟固结。

图6 模型试验加载装置和底板试件Fig.6 Model test loading system and bottom plate specimen

针对断索和主梁损伤，开展典型损伤下斜拉桥的性能退化模型试验。通过花篮螺丝调整索力以及拆卸钢丝绳模拟拉索断裂，改变主梁损伤区域的底板厚度模拟斜拉桥主梁不同程度损伤。钢主梁上3 处主梁损伤位置如图7 所示，位置编号分别为Db1，Db2和Db3，每个损伤区域宽度均为100 mm。正常工况下主梁的底板厚度为6 mm。当主梁的底板厚度为2～5 mm 时，为模拟主梁不同程度损伤，设置各损伤工况对应的主梁刚度参数如表4 所示。本试验共设计了21 组试验工况：1 组正常工况，8组拉索断裂工况，12 组主梁损伤工况。为测量斜拉桥在不同损伤工况下拉索索力、主梁内力及挠度等变化情况，试验共设置32 组应变测点，其中C1～C16为斜拉索上的应变测点，Y1～Y16为钢主梁上的应变测点，钢主梁上设置5组挠度测点，编号为L1～L5。测点布置如图7所示。

图7 测点布置示意图Fig.7 Schematics of measure points

表4 主梁损伤工况参数设置Table 4 Parameter setting of main girder damage condition

2 试验结果及分析

2.1 索力对比

为研究拉索断裂对其他索力的影响，按顺序依次拆除拉索S1～S8，进行下一组断索损伤工况前，恢复前一组拉索索力。图8 所示为拉索S1～S8依次断索后其他索力的分布图。由图8 可知：断索后，其他拉索均发生不同程度的索力重分配，不同断索工况引起的索力响应不同；断索后内力迅速向附近拉索转移，距断索位置越近，索力变化越大，如S4断索后，与其相邻的S3和S5的索力变化幅值较大。

图8 拉索断裂后索力分布情况Fig.8 Cable force distribution after cable rupture

为进一步定量研究拉索断裂对其他索力的影响，选取断索前后其他索力的变化进行对比，如图9 所示。图9 中，断索的索力变化值记为0 kN，其他索力变化值为损伤工况前后的索力之差。由图9可知：由于边界条件存在差异，与靠近主塔的短索和靠近边墩的长索相比，跨中断索对其他拉索影响更大，如拉索S4和S5断索后，其附近拉索的最大索力增量分别为25.5 N和27.4 N，而拉索S1和S8断索后，其附近拉索的最大索力增量分别为3.3 N和7.7 N。跨中断索后引起的最大索力增幅为74%，因此，在实际工程中，应提高跨中拉索的安全系数。

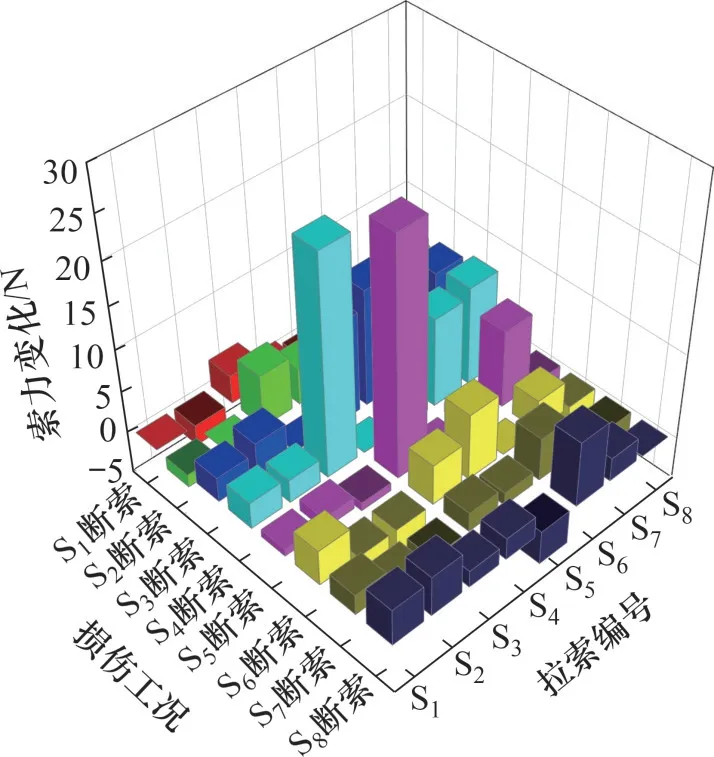
图9 断索工况前后索力变化Fig.9 Variation of cable force before and after cable rupture

图10 所示为2.0 kN 荷载作用下主梁发生不同程度损伤后引起的索力分布。图10中，2，3，4和5 mm为主梁损伤区域底板厚度，6 mm为正常情况下的主梁底板厚度，Db1～Db3为主梁损伤位置。由图10(a)，(b)和(c)可知：随着主梁损伤程度增加，模型桥的索力均有不同程度增加，主梁损伤程度越高，索力增幅越明显。如Db1位置主梁损伤后，拉索S2在底板厚度为6 mm时的索力为6.6 N，在底板厚度为2 mm时的索力为11.7 N，增幅为77.5%。图10(d)所示为底板厚度为2 mm 时，主梁在Db1，Db2和Db3处发生损伤后的索力分布，图中，“Db1-2 mm”表示Db1处的底板厚度为2 mm。由图10(d)可知：靠近边墩Db3处的主梁损伤对全桥索力影响最明显，与Db1和Db2处的主梁损伤相比，Db3处主梁损伤引起的全桥索力平均增幅分别高10.03%和29.42%。这说明靠近边墩的主梁对全桥索力起着重要的调控作用，该区域主梁发生损伤后，将引起全桥索力重分布。在实际工程中，应加大该区域的承载力储备并优化该区域混凝土结构抗裂性设计。

2.2 应力对比

图11 所示为2.0 kN 荷载下拉索断裂后主梁的应力分布图，其中，“▲”表示断索在主梁上的锚固位置，主梁的起点位置为图7中O点。斜拉索以一定角度锚固在主梁上，拉索张力使得主梁产生内力。断索导致其他索力改变，进而影响主梁内力分布。由图11 可知：断索后主梁局部支承条件发生变化，拉索锚固点所在的主梁区段应力增幅最大。如S6发生断索后，锚固区域的应力最大增幅为 10.7 MPa，其他主梁区域的应力增幅无明显变化。不同断索工况下主梁的应力分布不同，靠近主塔处的短索断索后对主梁应力分布影响较小，这是因为其索力较小且靠近塔墩梁固结区域；靠近边墩处的长索索力也较小，断索对主梁应力分布的影响不明显。跨中区段主梁仅靠斜拉索支承，当锚固在主梁跨中区域的拉索失效后，主梁应力增幅较大。如S1断索后，其锚固区段的应力增幅为1.3 MPa，当S4和S5断索后，锚固区段的应力增幅分别为18.5 MPa 和13.2 MPa，分别是S1断索引起应力增幅的14.2倍和10.1倍。

图11 断索工况后主梁应力Fig.11 Stress of main girder after cable rupture

图12 为2.0 kN 荷载下主梁发生不同程度损伤后的应力分布图，图中“▲”表示Db1，Db2和Db3损伤位置在主梁上的布置位置。由图12 可知：主梁发生损伤后，其截面特性迅速降低，不同位置的主梁发生损伤后其应力分布均发生明显变化；主梁损伤程度越高，主梁应力增幅越明显。如在主梁Db1位置发生损伤后，与主梁损伤底板厚度6 mm 的工况相比，在主梁损伤底板厚度为2，3，4 和5 mm 时，主梁4l/9 处应力分别增加了5.4%，15.5%，25.6%和30.5%。主梁发生损伤后应力变化较断索后小，这是由于斜拉桥为复杂超静定结构，主梁发生损伤后，损伤位置附近梁段应力首先发生变化，进而导致锚固在该梁段区域的拉索张力发生改变，使得全桥索力和应力重新分布。与跨中主梁损伤(Db2位置)和靠近边墩的主梁损伤(Db3位置)相比，靠近主塔处主梁损伤(Db1位置)对主梁应力分布影响较小。随着损伤由主塔向边墩前移，主梁应力增幅越大，图12(c)中主梁Db3位置处损伤引起全桥的应力增幅最大，进一步验证了“应加大主梁跨中到边墩区域的承载力储备及优化该区域混凝土抗裂设计”的结论。

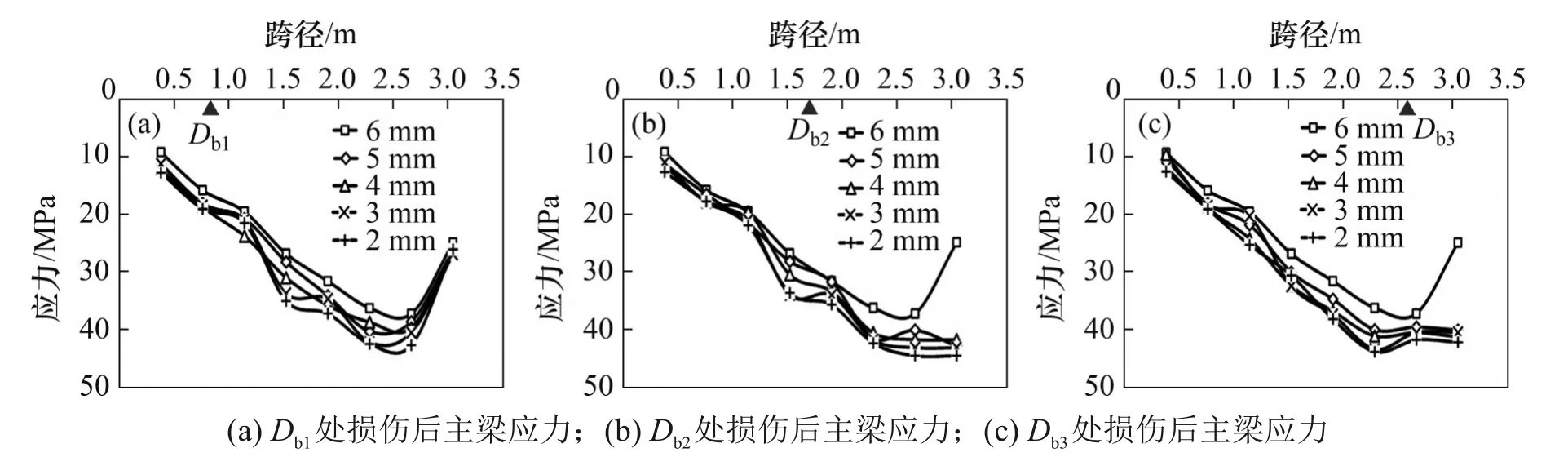
图12 主梁损伤后应力Fig.12 Stress of damaged main girder

2.3 主梁挠度对比

图13 为2.0 kN 荷载下拉索断裂前后主梁的挠度变化。拉索为斜拉桥主梁提供多点弹性支承，断索改变了主梁的局部支承条件，不同断索工况导致主梁挠度变化存在差异。由于缺少拉索的弹性支承，断索锚固点所在的主梁区段挠度变化较大。如S3发生断索后，其锚固点所在的主梁挠度最大增加2.71 mm(增幅为40%)。对比靠近主塔的短索和靠近边墩的长索，主梁跨中区段仅靠拉索支承，因此，锚固在跨中区域的拉索断裂后，对主梁挠度影响最大。如跨中S4断索后，引起的主梁挠度增幅分别为S1和S8断索后的4.32倍和6.98倍。由于拉索S7和S8靠近边墩，边墩竖向支承作用使得在S7和S8断索后的主梁挠度变化并不明显。

图13 断索工况后挠度Fig.13 Deflection of broken cable

2.0 kN荷载下主梁在不同位置发生不同程度损伤后的挠度变化如图14所示。由图14可知：主梁损伤后的挠度变化较断索小。这是由于主梁发生损伤后，拉索张力和主梁应力重新分布，主梁和拉索承受的内力均增加；同时，主梁发生损伤后并未改变主梁的局部边界条件，主梁损伤后挠度变化不明显。相比较而言，主梁Db2发生损伤后，对主梁跨中挠度影响较大。这是由于Db2位于主梁跨中，损伤导致该截面刚度减少，从而在荷载作用下该截面的挠度显著增加。

图14 主梁损伤后挠度Fig.14 Deflection of damaged main girder

图15所示为主梁Db2位置发生不同程度损伤时各测点的荷载-挠度关系曲线。由图15可知：在相同荷载下，随着损伤程度增加，主梁挠度逐渐增加，如在底板厚度为2 mm 时，2.0 kN 荷载时主梁跨中挠度为5.86 mm，是正常底板厚度6 mm 时的1.1 倍。在荷载作用下，挠度近似呈线性增大。随损伤程度增大，荷载-挠度曲线的斜率逐渐减小，这说明当主梁损伤程度较大时，荷载对主梁刚度退化影响显著。因此，对于服役较长时间的斜拉桥，应限制车流量和车辆载荷。

图15 主梁不同程度损伤后荷载-挠度曲线Fig.15 Load-deflection curves of main girder after different degrees of damage

3 结论

1)采用刚度相似理论设计的模型能较好反映原型桥的实际受力状况。

2)斜拉索断裂后，内力迅速向附近拉索转移，距断索位置越近，索力变化越大，断索锚固的主梁区段挠度和应力增幅均较大。跨中断索后引起的索力最大增幅为74%，跨中断索引起的主梁应力和挠度增幅分别比靠近主塔的短索和靠近边墩的长索高14.2 倍和6.98 倍，建议提高跨中拉索的安全系数。

3)主梁损伤程度越高，索力增幅越明显，靠近边墩的主梁区域对全桥索力和主梁应力有重要的调控作用，在实际工程中，应加大该区域的承载力储备和抗裂性设计。

4)随着主梁损伤程度增加，主梁挠度逐渐增加，主梁损伤程度最大时的挠度是正常情况下的1.1 倍。荷载对主梁损伤后的刚度退化作用效果显著，对服役较长时间的斜拉桥应限制车流量和车辆载荷。

5)拉索索力、主梁应力和挠度等指标对不同损伤工况的敏感性均不同，利用该特性可对斜拉桥损伤进行识别。

6)本研究仅针对单对断索或单个主梁节段不同程度损伤等工况，未考虑多对断索或不同程度损伤以及多段主梁同时损伤等工况，同时也未考虑断索对桥塔和主梁动力冲击作用的影响。下一步应考虑实际断索的动力冲击过程以及服役斜拉桥中存在损伤随机性。