考虑替开与均衡性的城轨列车运行调整

楚彭子 虞 翊 董丹阳 袁建军 陈义军

(同济大学道路与交通工程教育部重点实验室1) 上海 201804) (同济大学磁浮交通工程技术研究中心2) 上海 201804)

0 引 言

城市轨道交通(城轨)系统具有大运量与高密度运行的特征，由不确定因素造成的运行延误与中断事件，根据运行计划偏离程度，可分为扰动和中断[1]．扰动所造成的列车延误较小，可通过改变停站时间、折返时间和区间运行速度等方式恢复运行计划．中断的影响程度则较大，通常需要采用跳停、加开、减少线上列车、变更交路等措施．

制定可靠的列车运行调整方案，提高乘客出行的顺畅性一直是国内外研究热点．柏赟等[2]关注了列车运行的总晚点时间和到发均衡性，构建了列车运行调整模型，并借助遗传算法进行求解．针对因初始延误较大导致初始延误列车与前方列车(前车)之间运力不足的现象，刘峰博等[3]以乘客出行总时间最小为目标建立了优化模型，并设计了组合动态规划求解算法．卢佐安等[4]探讨了延误条件下列车“跳停”策略，构建了混合整数规划模型，并设计嵌套式遗传算法进行求解．将初始延误列车的前车纳入考虑范围，卢佐安等[5]进一步提出含有赶点、扣车、跳停的列车运行全过程调整方法，涉及以乘客旅行总时间最小的优化模型和嵌套式遗传算法．针对故障后的运行调整，Gao等[6]通过引入“跳停”方案，建立了以提高列车周转速度和降低乘客等待时间为目标的整数规划模型．Yin等[7]探讨了增开备车与调整列车运行次序的手段来尽快疏散站台滞留乘客．何占元等[8]针对故障结束、线路恢复阶段客流需求，综合考虑正线列车、备车及车辆段列车，结合“跳停”策略构建了以列车到达终点站时间总和最小为目标的优化模型．

综上，总晚点时间、到发均衡性、列车运行效率,以及乘客出行总时间等为列车运行调整常见优化目标，而跳停、加开备车或车辆段列车、赶点、扣车等为常见优化策略．值得关注的是，作为一种列车运行调整策略，“替开”的应用尚未得到充分讨论，尤其是针对初始延误较大的场景．同时，提高列车到发均衡性有助于保证乘客服务水平．基于此，文中针对因车辆故障导致较大初始延误的情形，以“替开”为手段，兼顾列车到发均衡性以及总晚点时间，开发多目标优化模型与算法，为相应场景下列车运行调整制定可行方案．

1 模型准备

1.1 问题描述

图1为考虑替开的列车运行调整示意图．列车i在车站3突发车载信号设备故障只能降低驾驶模式低速运行，若列车按该模式运行至终点站，势必会影响其后方列车，导致较大的晚点．此时，如果车站4具备存车线，且存车线存有一列备车，则可使用备车“替开”列车i车次，还可将列车i尽快停放在车站4存车线上，以降低对后车的影响，见图1中虚线．值得注意的是，由列车i导致的初始延误可能对列车服务的均衡性产生影响，很容易造成类似于列车i和列车i-1之间运力不足的现象．

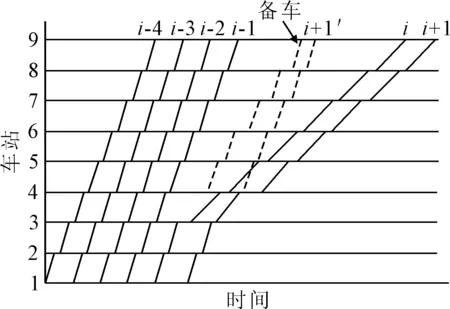
图1 考虑替开的列车运行调整示意

针对图1所示的服务不均问题，文中通过控制前车晚点时间，并协调备车与前车，以使得运行计划恢复期间列车的到发时分更加均衡．也就是说，该问题可理解为如何调节不同列车在不同车站的到发时分来保证运行计划恢复期间列车服务的均衡性以及准时性．

1.2 假设条件

根据图1场景特征及问题范围，结合城市轨道交通运营需求，给出了以下基本假设.

假设1列车运行顺序是已知的，不存在次序变化的情况．

假设2客流相对较小，较小延误不至于导致客流大范围拥堵的情况．

假设3列车采用站站停的运行方式，无“跳停”运行的情况．

假设4涉及的场景中只需一列备车就可以较好地服务乘客，且备车存放或上线位置距离初始延误发生位置较近．

假设5类似于文献[3]，初始延误列车及其后方相邻列车的调整方案与前车运行计划是已知的．

1.3 符号定义

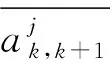
1.4 模型构建

文中考虑的基本问题是如何在总延误尽可能小的前提下尽可能提高列车服务的均衡性．由于初始延误列车的处置方案及初始延误列车后方相邻列车的调整方案已知，且部分前车的调整路径有限，因此总延误最小应为备车(相对于初始延误列车而言)与前车的总延误最小，且备车与前车需要经过的车站是已知的．此时，对于k∈M∪{l}，j∈Sk，总延误时间最小可表示为

(1)

同时，根据相同车站不同列车的到达时分与发车时分，可借助到达间隔与出发间隔的方差来表示均衡性．此时，对于k,k+1∈M∪{l,ib}，j∈Sk，均衡性尽可能好为

(2)

进一步地，模型的约束条件包括：列车运行间隔约束、备车上线时间约束、延误时间约束、站停时分约束、决策变量边界约束，以及区间运行时分约束等．其中，对列车运行间隔时间进行约束是为了保证列车运行的安全性，涉及列车的追踪间隔不能小于最小追踪间隔，列车的发到间隔不能小于最小发到间隔．此时，对于k,k+1∈M∪{l,i-,ib}，j∈Sk，有：

(3)

(4)

ak+1,j-ak,j≥Ih

(5)

dk+1,j-dk,j≥Ih

(6)

ak+1,j-dk,j≥Ip

(7)

除了正常的追踪间隔要求外，为了保证安全，采用较低驾驶模式时还需要考虑其他安全边界．例如，以RM(人工驾驶)模式运行的列车通常还需要与前车保持“一站一区间”的间隔．以该情形为例，初始延误列车前方可能是备车，也可能是可调整的正常列车．此时，对于i∈M，j∈Si，如果有di-,j>ts，则：

max(di,j+1,dl,j+1)≤di-,j

(8)

同时，备车达到正线车站所需满足的时间约束为

al,sl≥ta+ts

(9)

(10)

(11)

ai,j-Ai,j≥0

(12)

di,j-Di,j≥0

(13)

要求列车站停时分不能过短，也不能太长．即对于k∈M∪{l}，j∈Sk，有：

(14)

(15)

由于前车计划时刻表、初始延误列车处置方案和初始延误列车后方相邻列车调整方案均为已知，可设置前方边界约束与后方边界约束分别为

ai,j=Ai,j,∀(i,j)∈{(i,j)|Ai,j≤ts+tp}

(16)

di,j=Di,j,∀(i,j)∈{(i,j)|Di,j≤ts+tp}

(17)

(18)

(19)

此外，考虑到乘客舒适性、列车以及线路条件，需设置运行时分约束．即对于k∈M∪{l}，j,j+1∈Sk，有：

ak,j+1-dk,j≥rj,j+1

(20)

2 算法设计

采用带精英策略的快速非支配排序遗传算法(NSGA-II)[9]，并设计相应的遗传算子．NSGA-II是一种基于群体演化的多目标遗传算法，算法流程见图2．与常规遗传算法不同，其个体的优劣程度根据目标函数值、约束违反(constraint violation,CV)值(存在约束条件时)、非支配排序(rank)和拥挤距离(crowding distance,CD)共同确定，所得的最优解为Pareto(帕累托)最优解集[10]．

图2 算法流程

图3位染色体编码．其中，对正线列车信息的编码为前车计划到发时分的增加量，对备车信息的编码为初始延误列车计划到发时分的增加量．解码时，只需在计划到发时分的基础上加上相应的增加量．其中，若时间点的总数为n，前车到站时分和出发时分个数为w，则备车的时间点个数为n-w．同时，为便于个体操作，将目标函数值、约束违反(CV)值、非支配排序(Rank)与拥挤距离(CD)等信息存放于染色体尾部．

图3 染色体编码

由于决策变量多，约束条件复杂，根据优化目标与问题特征设计了相应的种群初始化方法．该方式是在较小的范围内生成随机量作为正线列车与备车的延误时间．随机量面向列车到发的均衡性，因个体与列车的不同而不同，并随着列车经过车站的数目递增．例如，对于个体cp，列车q在某车站的随机量为δq，则相应的编码值为δp,q，解码值为aq+δp,q或dq+δp,q．

个体选择采用了二元锦标赛选择法．该方法随机挑选两个个体，优先选择非支配排序小的个体(即精英个体)作为父代个体．若个体排序一致，则选择拥挤距离大的个体．若等级与距离相等，则随机选择其中的一个．同时，替换操作也遵循该原则．对于交叉与变异，文中随机选取操作位置，见图4．该方式是一种全局的交叉与变异方式．

图4 交叉和变异算子

3 仿真算例

3.1 算例描述

以文献[4-5]中基础数据为例，涉及线路有20座车站，车站11存放有备车．假设列车9在07:10:30于车站8～9运行时突发故障．调度员于07:12:45下发列车运行调整方案，要求列车9降级运行至车站11存车线抢修，并启动备车“替开”相应车次．运行调整中晚点车次统计的参考值为300 s，列车最大、最小站停时分分别为300 和25 s．同时，列车计划追踪间隔为180 s，最小追踪间隔为120 s，最小发到间隔为80 s，计划站停时分Tw(s)、计划区间运行时分RP(s)与最小区间运行时分R(s)分别为：Tw=[40,40,40,35,40,30,35,30,35,35,35,30,40,35,30,30,30,30,30,30]，RP=[130,96,105,85,89,79,76,90,85,89,93,107,101,78,82,78,83,93,110]，R=[104,77,84,68,71,63,61,72,68,71,74,86,80,62,66,62,66,74,88]．

在NSGA-II算法参数方面，设置交叉与变异概率分别为0.9和0.09，种群规模为200，迭代次数为50．在种群初始化方面，根据可调整的前后边界以及被调整列车数量，将每列列车到发时分随机调整量范围分别设置为[0,32]、[0,64]、[0,97]、[0,129]、[0,162]、[0,194]、[0,227]与[0, 258](单位为s)，且调整量随列车运行时间递增．同时，个体编码的变异范围为[0,450]．算例的仿真过程借助了matlab软件．

3.2 结果分析

当采用调整量递增的方式来获取初始种群时，初始种群中的可行解有177个，而仅采用随机调整量时通常不存在可行解，即调整量递增的方式适用于本文模型与算法．同时，算法运行时间为51.5 s，速度较快．图5为NSGA-II算法得到的Pareto最优前沿，该Pareto最优解集中存在11个最优解，解的分布较为均匀．

图5 Pareto最优前沿

实际中，具体调整方案可根据决策偏好进行选取．例如，选取目标函数1最优的解或目标函数2最优的解作为列车运行调整方案，也可以选择两目标均相对较优的情况．该标记显示其目标函数1的值为5 106，目标函数2的值为75 206.1，对应的列车运行调整方案见图6．

图6 考虑备车与均衡性的运行调整

由图6可知：前车调整计划向右侧逐渐倾斜，保证了较好的均衡性，而种群初始化方式也采用了该思路．同时，前车调整计划存在一定的延误，但延误时间在可接受的范围内．其中，前车的最大延误时间为191 s，为列车8到达终点站的时间．备车的最大延误时间为253 s，也满足约束条件．在列车的站停时分方面，最大站停时分为71 s，最小站停时分为30 s，均满足要求．此外，图中最小追踪间隔为166 s，最小发到间隔为130 s，同样满足约束．因此，文中模型与算法是有效的．

4 结 束 语

总延误时间与到发均衡性是列车运行调整中常见指标．在初始延误较大时，如何协调这两方面的需要，保证服务质量值得关注．文中针对备车“替开”初始延误列车背景下的列车运行调整，设计了双目标优化模型及其求解算法．有关增开多个备车及“跳停”情形下考虑均衡性的列车运行调整有待进一步研究．