马尔科夫预测法评估某院血液科药品不良反应报告数量*

黄 莺，方 明，李 民

（中国科学技术大学附属第一医院·安徽省立医院药剂科，安徽 合肥 230001）

我国每年约有超过250 万人次发生药品不良事件［1-2］。医院是上报药品不良事件的重要来源，药学人员需熟练掌握临床用药的作用特点、药品不良反应（ADR）、相互作用等，发现、收集、上报、分析和监测ADR 报告信息，用于日常药物安全性监测工作［3］。目前，比值失衡测量法为监测ADR 最常用的方法［4］。由于ADR 发生的随机性，一般用于随机性过程的预测方法难以监测日益增加的ADR。马尔科夫预测法（简称马尔科夫法）是一种科学的随机过程的预测法，是对事件的全面预测，不仅能指出事件发生的各种可能结果，且能预测每种结果出现的概率［5］，具有科学性、实效性等特点，已逐渐运用于多个领域［6-10］。药品在治疗疾病的同时，其在人体内的吸收、分布、代谢、排泄符合马尔科夫过程［11-12］。在一段时间内，ADR 发生数量的序列可看作一种离散的随机过程，过程满足马尔科夫链的条件。为此，本研究中基于马尔科夫法预测医院血液科ADR发生状态的合理性，监测ADR 上报数量，以督促各病区真实、合理上报ADR。现报道如下。

1 资料与方法

1.1 资料来源

收集我院药剂科2018 年1 月至2019 年11 月上报的血液科ADR数据。

1.2 方法

马尔科夫链是一种随机、无后效性的时间序列。定义为若一个非负随机序列｛X（tn），n∈N｝满足条件，Xt-1= i，即随机序列过程在时刻t- 1 的状态为i，则在下一时刻tn序列的状态只与tn-1时刻状态i 有关，而与前面各个时刻的状态无关，则该随机序列｛X（tn）｝称为马尔科夫链［13］。

马尔科夫链的要素包括时间集［14］，即时间（t）所构成的集和，t=｛0，1，2，…｝；状态集，即状态i 的集合，i=｛1，2，3…，n｝，n为有限量；初始状态i0，既可以是一个变量，也可以是一个固定值。状态转移为在一个系统中事物变量的状态由某一种状态变化、转移到另一种状态的过程，其转移概率所构成的集合为概率矩阵。矩阵中各元素都是非负的，且各行元素之和等于1，各元素用概率表示，在一定条件下是互相转移的，故称为状态转移概率矩阵［15］。在随机序列｛X（tn）｝中，若由Xn=i 转移到Xn+1=j 的概率Pij与n无关，则该转移称为一步状态转移［16］。矩阵见（1）。

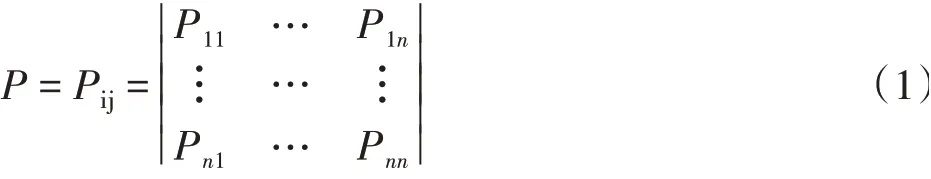
k步转移概率矩阵Pij（k）指的是事物过程从状态i经过k步转移后达到状态j 时概率所构成的矩阵［17］。矩阵见（2）。

本研究中模型构建的大体步骤［18］：1）统计满足统计性、随机性的数据，建立标准、划分状态；2）将两两相斥事件i1，i2，...，in状态拟合成马尔科夫链序列；3）采用矩阵实验室（MATLAB）程序计算序列，结果得到不同的转移概率矩阵，矩阵中最大转移概率即为预测结果；将预测结果与实际进行比较。

某种方法对某件事情作出预测时，由于各种因素的干扰，预测结果不可能100%正确，结果都是以大概率发生的情况为参考值。为验证马尔科夫法能预测ADR状态，本研究中选取部分相关数据分步计算。

2 结果

2.1 ADR 发生的例数

于ADR 报告数据库中选取我院血液科2018年1月至2019年11月上报的数据，共3 088例。每月的ADR 发生数据见表1。

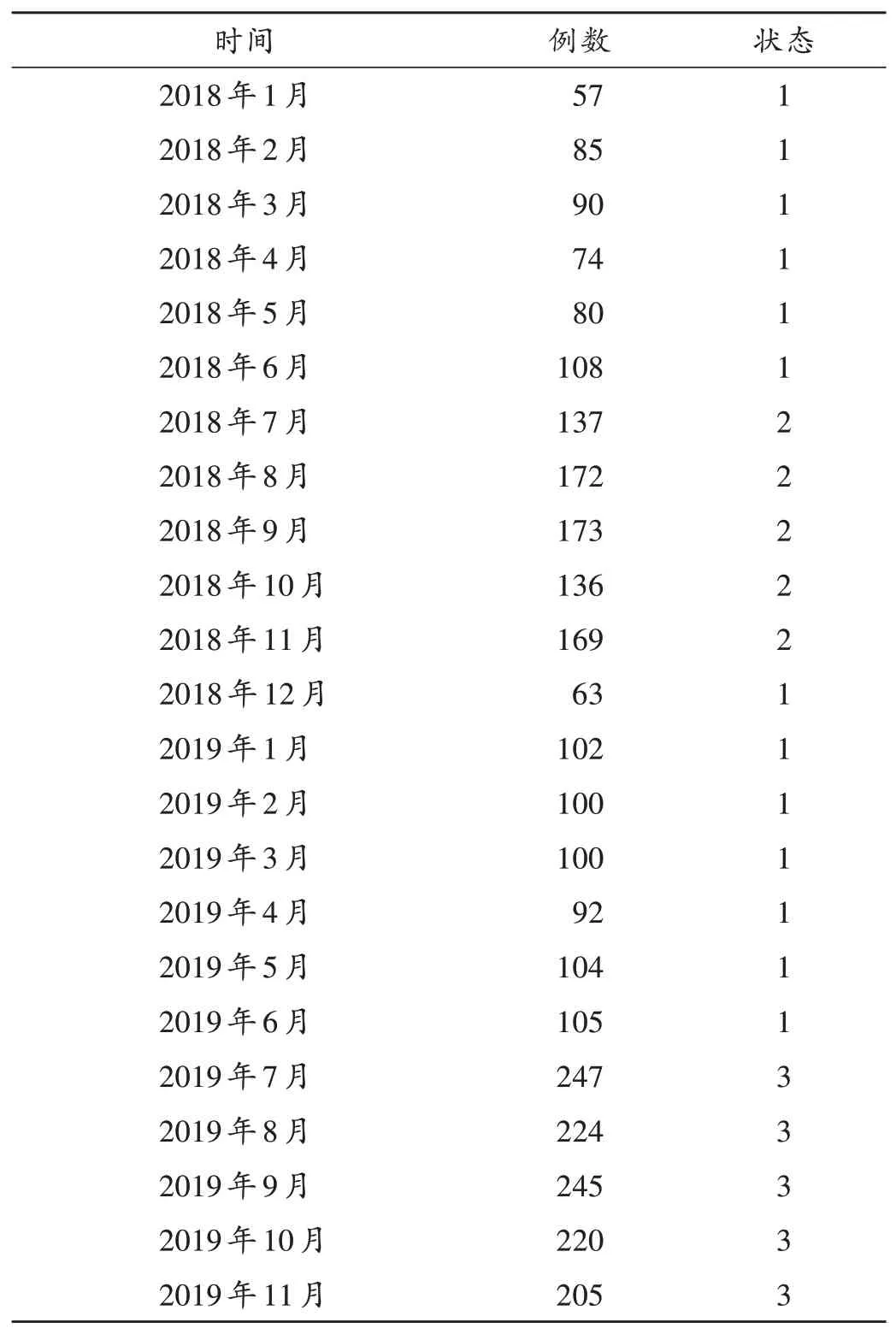
表1 2018年1月至2019年11月血液科药品不良反应发生例数与状态Tab.1 Cases and occurence status of ADR in the Department of Hematology from January 2018 to November 2019

2.2 ADR 发生的状态

根据方法中模型的构建，采用三分法划分ADR 发生的状态。即区间状态f=（Xmax-Xmin）/3，令Xmax-f＜i3＜Xmax为状态3 级，Xmax-2f＜i2＜Xmax-f为状态2 级，i1＜Xmin+f为状态1 级。式中，Xmax和Xmin分别为表格数据中的最大值和最小值。各数据按分级标准、状态分布，详见表1。

2.3 ADR 状态的预测

由表1 可知，2018 年1 月至2019 年11 月每月的状态以连续前12 个月为1 个序列拟合成马尔科夫链，再用MATLAB 程序对该序列进行计算，预测第13 个月的结果，详见表2。可知，在11个序列中，有7个符合，有2个不符合，因数据不符合马尔科夫链的过程，故程序无法计算的有2个，符合情况下的概率计算结果为63.64%。

表2 2018年1月至2019年11月药品不良反应状态的预测结果Tab.2 Prediction results of ADR status from January 2018 to November 2019

2.4 预测结果分析

本研究结果表明，采用马尔科夫法对ADR 进行预测时，具有一定的准确性及可靠性。当出现预测结果与实际情况不符时，可能是由于事物的发生具有众多的随机性；同时，马尔科夫法也为一种概率预测方法，仅靠实验方法选取的部分数据，用频率出现的次数还不足以代表事物发生的概率。由表2 可知，出现无法计算的结果，可能是由于MATLAB 程序不稳定及序列数据链不够长造成的。为防止该影响的发生，以及减少实验具有偶然性而出现不具代表性的数据，应选取更多的数据为序列进行计算。故在后续实验计算中，应选取更多的数据作为支撑，实验方案也有待进一步探讨。

3 讨论

马尔科夫链的性质包括以下4 个：1）无后效性，事物变量在将来的取值只与现在有关而与过去无关；2）平稳分布性，某一时刻的状态概率向量分布情况平稳的随机过程；3）稳态分布性，对于系统的状态P（m），当m趋于无穷时，存在一个极限稳态分布π；4）状态相通性，即系统中的变量经过有限步转移后均可达到同一状态［19］。

本研究中通过马尔科夫法预测ADR 的情况，为ADR 监测提供全新的信号挖掘方法。ADR 上报是保证用药安全的重要因素，医院各个病区作为ADR 上报的主要来源，上报的及时性、准确性关系着临床医师的合理用药及患者的用药安全。为此，根据已发生的ADR 数量预测未发生的ADR 状态，采用马尔科夫法评估某个病区上报的ADR 报告数量在未来的周期是否存在异常，监测被动上报的ADR 报告数量是否正常，以此督促病区真实、合理上报ADR，对于加强医师、护士及临床药师间的合作具有积极意义。