二维瞬态热传导的PDDO 分析*

周保良， 李志远， 黄 丹

（河海大学 力学与材料学院，南京 211100）

引 言

瞬态热传导问题是航空航天、机械化工、生物工程等领域关注的重点[1].近年来，相关领域的研究者们分别采用有限单元法(finite element method, FEM)[2-3]、局部径向基函数微分求积法 (radial basis function-based differential quadrature, RBF-DQ)[4]、边界单元法(boundary element method, BEM)[5]、边界节点法(boundary knot method, BKM)[6]、双重互易边界元法(double reciprocal boundary element method, DRBEM)[7]、Trefftz 有限元法(Trefftz finite element method, Trefftz FEM)[8]等各种数值方法求解了材料和结构的瞬态热传导问题.在各种数值方法中，近场动力学(peridynamics, PD)方法[9-10]用积分方程代替经典连续介质力学中的偏微分方程，避免了基于连续性假设建模和求解微分方程时的传统方法在不连续问题中的奇异性.最新的近场动力学微分算子(PDDO)[11-12]是基于PD 非局部思想和PD 函数的正交性提出的一种非局部算子，通过Taylor 级数展开和正交函数的性质建立了局部偏导数和非局部积分之间的联系.PDDO 的优势不仅体现在可以求解复杂的微分方程，而且能够在不连续点或奇异点存在时计算光滑或分散数据的导数值.此外，PDDO 不限制对空间和时间变量求偏导的顺序，当考虑时间非局部性或者更广义的时空非局部性时，PDDO 将会有广阔的适用性.目前该方法已成功应用于液体晃荡[13]、复合材料[14-15]、热流耦合[16-17]、热力耦合[18]等问题分析.

本文针对二维瞬态热传导问题，基于PDDO 理论进行求解.首先将热传导方程和边界条件进行Taylor 展开，通过构建PD 函数，利用正交性将微分方程重构为积分形式，引入Lagrange 乘子，进行变分分析，建立了二维瞬态热传导问题的非局部分析模型，然后通过三个算例验证了PDDO 计算二维瞬态热传导问题具有收敛速度快，计算精度高，适用性好等特点.

1 基本理论和模型

1.1 近场动力学微分算子理论

如图1 所示，在一个三维空间D中，物质点x=(x1,x2,x3)在近场范围Hx内与另一个物质点x′=(x1′,x2′,x3′)相互作用，ξ=x′−x是这两个点之间的初始相对位置，δ 表示近场范围Hx的大小.

图1 物质点在任意形状近场范围内的相互作用Fig. 1 Interaction of material points within an arbitrary-shape near field

事实上，PDDO 可考虑在M维空间中对标量场函数f(x′)=f(x+ξ)在点x处进行N阶Taylor 级数展开[11]：

其中R(N,x)是展开余项，ni表示对xi微分的阶数.

其中δnipi表示Kronecker 符号.

将PD 函数构造成多项式形式：

由此，可以将式(5)用矩阵的形式表达为

由式(8)可得待求系数矩阵a，代入式(4)可得PD 函数，进一步通过式(2)确定局部微分的PD 形式.

1.2 二维瞬态热传导的PDDO 模型

在直角坐标系下无热源的二维瞬态热传导方程由下式确定[19]：

其中T(x,y,t)表示温度，α表示导温系数.定解条件如下：

初始条件

温度边界条件

绝热边界条件

其中L和C分别是二维瞬态热传导方程和定解条件中含PD 函数的系数矩阵，向量d是定解条件中离散点上的已知值，向量T表示离散各点处的待求温度.

在式(18)中引入Lagrange 乘子λ，并利用变分原理的概念[11]，可以得到

将式(19)中第二项展开，得到

2 数 值 算 例

2.1 误差与收敛性分析

考虑一块尺寸为3 m × 3 m 的方板，边界条件如图2 所示.其中导温系数α=1.25 m2/h，初始温度为T0=30 ℃，取PD 物质点之间离散间距Δx=Δy=0.075 m，Δt=0.075 h.

图2 方形板及边界条件Fig. 2 A square plate and its boundary conditions

该问题的解析解[6]为

其中

在该方形板中，取表1 所示的5 个测点，计算当t=1.2 h 时测点处温度，并与解析解和不同数值方法[5-8]比较.从表中数据可见PDDO 与解析解和其他数值解基本一致，且具有较高精度.

表1 t=1.2 h 时不同方法的数值结果比较Table 1 Comparison of numerical results between different methods at t =1.2 h

图3 为全局误差测量方法[20]下，PD 物质点间距分别取0. 075, 0.1, 0.15 时的误差测量值，误差ε 计算公式为

其中，|T(e)|max为解析解求得温度绝对值的最大值，上标e 和c 分别表示精确解和本文模型解，参数K表示离散后PD 点的总数.图3 折线中每段直线斜率的平均值表示收敛速度，其值为4.82.从图中可以看出，随着物质点间距的减小，全局误差逐渐减小，数值解逐渐收敛于精确解，说明本文模型具有良好的收敛性.

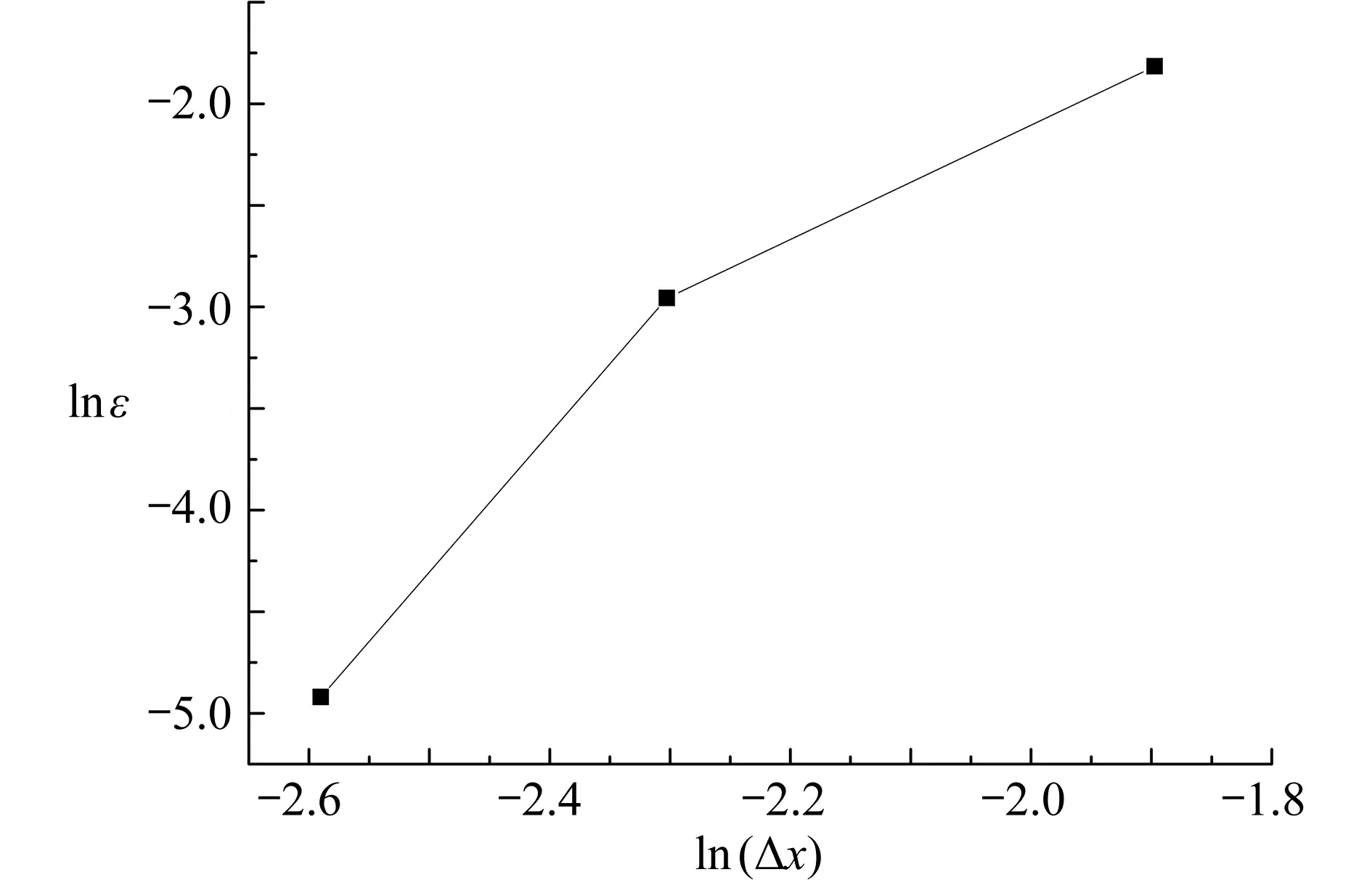
图3 瞬态温度场的PDDO 误差测量值Fig. 3 The error measure of the PDDO solution for the transient temperature field

2.2 不规则边界板的二维瞬态热传导分析

A、B、C 三种形状板的边界条件如图4 中标注所示，其中导温系数α=17.95 m2/s，初始温度为T0=0 ℃,取PD 物质点之间离散间距Δx=Δy=0.025 m，Δt=0.025 s.

图4 A、B、C 板的几何形状和边界条件Fig. 4 Geometric shapes and boundary conditions of plates A, B and C

图5 为t=0.8 s 时，A、B、C 三种形状的板在不同数值方法下[21]，沿指定路径的温度分布曲线.从图中可以看出PDDO 方法与FEM 和RBF-DQ 方法得出的结果一致.到达稳态后，图6～图8 分别给出运用本文模型与上述方法求解板内温度的对比情况.结果表明，通过PDDO 计算二维瞬态热传导问题是一种新颖且有效的方法，即使对于复杂的不规则边界问题也具有较高的精度.

图5 t=0.8 s 时，A、B、C 三种形状的板在不同方法下沿指定路径的温度分布Fig. 5 Temperature distributions of plates A, B and C along a specified path for different methods at t=0.8 s

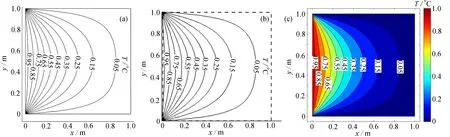
图6 稳态时，A 板在不同数值方法下的温度分布：（a） FEM[21]；（b） RBF-DQ[21]；（c） PDDOFig. 6 Temperature distributions of plate A for different numerical methods in a steady state: （a） FEM[21]; （b） RBF-DQ[21]; （c） PDDO

图7 稳态时，B 板在不同数值方法下的温度分布：（a） FEM[21]；（b） RBF-DQ[21]；（c） PDDOFig. 7 Temperature distributions of plate B for different numerical methods in a steady state: （a） FEM[21]; （b） RBF-DQ[21]; （c） PDDO

图8 稳态时，C 板在不同数值方法下的温度分布：（a） FEM[21]；（b） RBF-DQ[21]；（c） PDDOFig. 8 Temperature distributions of plate C for different numerical methods in a steady state: （a） FEM[21]; （b） RBF-DQ[21]; （c） PDDO

注 为了解释图中的颜色，读者可以参考本文的电子网页版本，后同.

2.3 含裂纹板和含圆孔板的二维瞬态热传导分析

图9 为含绝热裂纹和绝热圆孔的2 m × 2 m 方板几何模型示意图.裂纹尺寸为1 m × 0.05 m，圆孔半径为0.1 m.板的导温系数为α=0.1157 m2/d，初始温度为T0=0 ℃，Γ1和Γ3分别表示T=100 ℃与T= −100 ℃的温度边界条件，Γ2和Γ4表示绝热边界条件，测点1 分别位于裂纹尖端处和圆孔的斜下方.

图9 含裂纹板和含圆孔板模型Fig. 9 The models for plates containing a crack or a hole

该问题中，PD 物质点之间离散间距为Δx=Δy=0.05 m，Δt=0.05 d.如图10 和图11 所示，将有限元软件ANSYS 与PDDO 方法模拟的稳态结果进行对比，结果表明通过两种方法得到的含裂纹板的温度分布基本一致.

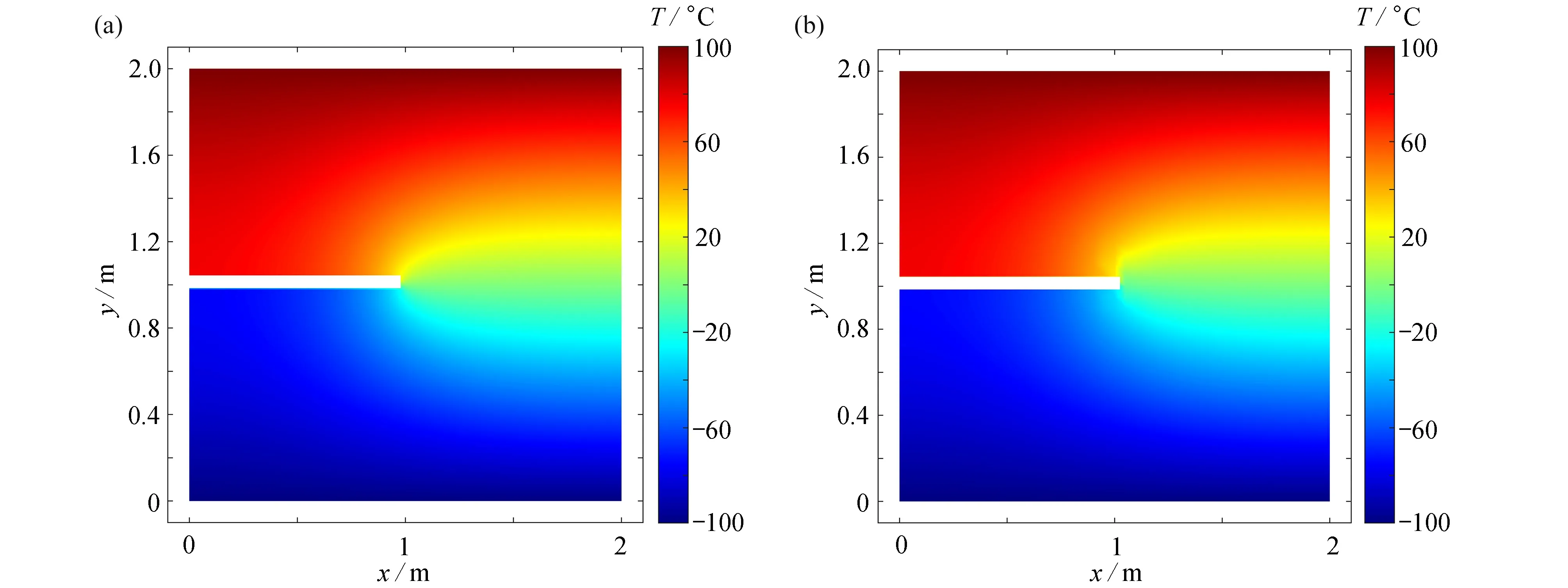
图10 稳态时，含裂纹板在不同数值方法下的温度分布：（a） FEM；（b） PDDOFig. 10 Temperature distributions of plates containing cracks for different numerical methods in steady states: （a） FEM; （b） PDDO

图11 稳态时，含圆孔板在不同数值方法下的温度分布：（a） FEM；（b） PDDOFig. 11 Temperature distributions of plates containing holes for different numerical methods in steady states: （a） FEM; （b） PDDO

图12 给出了含裂纹板和含圆孔板通过ANSYS 和本文模型计算的温度变化曲线.其中图12(a)和12(c)给出了含裂纹板和含圆孔板在测点1 处温度随时间的变化曲线.图12(b)给出了达到稳态时，温度沿裂纹下边界变化的曲线.上述图中运用本文模型与ANSYS 模拟的结果吻合，证明了本文建立的二维瞬态热传导模型具有较高精度且能够处理含非连续结构的热传导问题.

图12 含裂纹板和含圆孔板在不同数值方法下的温度变化曲线：（a） 含裂纹板测点处，温度随时间的变化曲线；（b） 稳态时，温度沿裂纹的下边界变化的曲线；（c） 含圆孔板测点处，温度随时间的变化曲线Fig. 12 The temperature variation curves of plates containing a crack or a hole for different numerical methods: （a） temperature change curves with time at the measuring point of the plate containing a crack; （b）temperature curves along the lower boundary of the crack in a steady state; （c） temperature change curves with time at the measuring point of the plate containing a hole

3 结 论

本文将PDDO 方法应用于求解了二维瞬态热传导问题.将二维瞬态热传导方程和边界条件由其局部微分形式转化为非局部积分形式，引入Lagrange 乘数法并通过变分分析，求解了二维瞬态热传导问题的温度场.典型算例表明，基于PDDO 方法构建二维瞬态热传导的非局部求解模型，采用均匀布点离散求解域，避免了由于网格依赖性和网格加密而产生的求解效率低的问题，不仅对求解不规则边界板的瞬态热传导问题具有较高精度，而且也同样适用于含裂纹和含圆孔板等不连续问题.算例结果显示，PDDO 方法计算精度高、适用范围广，且具有较好的稳定性和收敛性，为求解二维瞬态热传导问题提供了新的思路，同时也拓宽了PDDO 方法的应用范围.

参考文献（ References ） ：

［1］王 红, 李小林. 二维瞬态热传导问题的无单元Galerkin法分析[J]. 应用数学和力学, 2021, 42（5）: 460-469. （WANG Hong, LI Xiaolin. Analysis of 2D transient heat conduction problems with the element-free Galerkin method[J].Applied Mathematics and Mechanics, 2021, 42（5）: 460-469.（in Chinese））

［2］Z IENIUK E, SAWICKI D. Modification of the classical boundary integral equation for two dimensional transient heat conduction with internal heat source, with the use of NURBS for boundary modeling[J].Journal of Heat Transfer, 2017, 139（8）: 81-95.

［3］B URLAYENKO V N, ALTENBACH H, SADOWSKI T, et al. Modelling functionally graded materials in heat transfer and thermal stress analysis by means of graded finite elements[J].Applied Mathematical Modelling,2017, 45（5）: 422-438.

［4］W U X H, TAO W Q. Meshless method based on the local weak-forms for steady state heat conduction problems[J].International Journal of Heat and Mass Transfer, 2008, 51（11/12）: 3103-3112.

［5］B REBBIA C A, TELLES J C F, WROBEL L C.Boundary Element Techniques:Theory and Applications in Engineering[M]. Berlin: Springer Verlag, 1984.

［6］师 晋红, 傅卓佳, 陈文. 边界节点法计算二维瞬态热传导问题[J]. 应用数学和力学, 2014, 35（2）: 111-120. （SHI Jinhong, FU Zhuojia, CHEN Wen. Boundary knot method for 2D transient heat conduction problems[J].Applied Mathematics and Mechanics, 2014, 35（2）: 111-120.（in Chinese））

［7］P ARTRIDGE P W, BREBBIA C A, WROBEL L C.The Dual Reciprocity Boundary Element Method[M].Southampton: Computational Mechanics Publications, 1992.

［8］J IROUSEK J, QIN Q H. Application of hybrid-Trefftz element approach to transient heat conduction analysis[J].Computers & Structures, 1996, 58（1）: 195-201.

［9］S ILLING S A, EPTON M, WECKNER O, et al. Peridynamic states and constitutive modeling[J].Journal of Elasticity, 2007, 88（2）: 151-184.

［10］黄 丹, 章青, 乔丕忠, 等. 近场动力学方法及其应用[J]. 力学进展, 2010, 40（4）: 448-459. （HUANG Dan, ZHANG Qing, QIAO Pizhong, et al. A review on peridynamics(PD)method and its applications[J].Advances in Mechanics, 2010, 40（4）: 448-459.（in Chinese））

［11］M ADENCI E, BARYT A, DORDUNCU M.Peridynamic Differential Operator for Numerical Analysis[M].Switzerland: Springer Nature Switzerland AG, 2019.

［12］M ADENCI E, BARUT A, FUTCH M. Peridynamic differential operator and its applications[J].Computer Methods in Applied Mechanics and Engineering, 2016, 304: 408-451.

［13］B AZAZZADEH S, SHOJAEI A, ZACCARIOTTO M, et al. Application of the peridynamic differential operator to the solution of sloshing problems in tanks[J].Engineering Computations, 2018, 36（1）: 45-83.

［14］D ORDUNCU M. Stress analysis of laminated composite beams using refined zigzag theory and peridynamic differential operator[J].Composite Structures, 2019, 218: 193-203.

［15］D ORDUNCU M. Stress analysis of sandwich plates with functionally graded cores using peridynamic differential operator and refined zigzag theory[J].Thin-Walled Structures, 2020, 146: 106468.

［16］G AO Y, OTERKUS S. Nonlocal modeling for fluid flow coupled with heat transfer by using peridynamic differential operator[J].Engineering Analysis With Boundary Elements, 2019, 105: 104-121.

［17］G AO Y, OTERKUS S. Nonlocal numerical simulation of low Reynolds number laminar fluid motion by using peridynamic differential operator[J].Ocean Engineering, 2019, 179: 135-158.

［18］L I Z Y, HUANG D, XU Y P, et al. Nonlocal steady-state thermoelastic analysis of functionally graded materials by using peridynamic differential operator[J].Applied Mathematical Modelling, 2021, 93: 294-313.

［19］C UI M, XU B B, FENG W Z, et al. A radial integration boundary element method for solving transient heat conduction problems with heat sources and variable thermal conductivity[J].Numerical Heat Transfer, 2018, 73:1-18.

［20］S OLEIMANI S, JALAAL M, BARARNIA H, et al. Local RBF-DQ method for two dimensional transient heat conduction problems[J].International Communications in Heat and Mass Transfer, 2010, 37（9）: 1411-1418.

［21］M UKHERJEE Y X, MUKHERJEE S. On boundary conditions in the element-free Galerkin method[J].Computational Mechanics, 1997, 19（4）: 264-270.