分数阶Cable 方程的有限点法分析*

陈虹伶， 李小林

（重庆师范大学 数学科学学院，重庆 401331）

引 言

Cable 方程是神经元动力学模型中最基本的方程之一[1]，分数阶Cable 方程从分数阶Nernst-Planck 方程导出[2]，是经典Cable 方程的推广，可用于模拟离子在棘状神经元树突中的异常电扩散过程.有限差分法[1,3-5]、有限元法[6]、谱方法[7]、径向基函数法[8]和无单元Galerkin 法[9]等数值技术已被广泛应用于求解分数阶Cable方程.

无网格法[10-12]在过去三十多年中得到了迅速发展，可有效克服有限差分法和有限元法等经典数值方法中网格单元带来的困难，同时具有较高的计算精度.有限点法[13-15]是基于移动最小二乘近似构造数值解和配点技术形成离散代数方程组的最流行和最简单的一种无网格方法，已成功求解了大量科学工程问题.目前，我们还没有发现用无网格有限点法研究分数阶Cable 方程的报道.

本文建立数值分析含有Riemann-Liouville 时间分数阶导数的Cable 方程的有限点法.首先，借鉴文献[5]用中心差分格式离散该方程中的时间导数；其次，用有限点法建立线性离散代数系统；然后，受文献[16]的启发推导求解了分数阶Cable 方程的有限点法的理论误差估计；最后，给出数值算例验证了该方法的有效性和理论误差结果.

1 数 值 算 法

考虑以下分数阶Cable 方程的初边值问题[9]：

2 误 差 分 析

并且由式(17)可以得出

根据移动最小二乘近似的重构性质[18]和式(13)，我们得到

根据式(8)，我们得到

将式(20)代入式(23)中，有

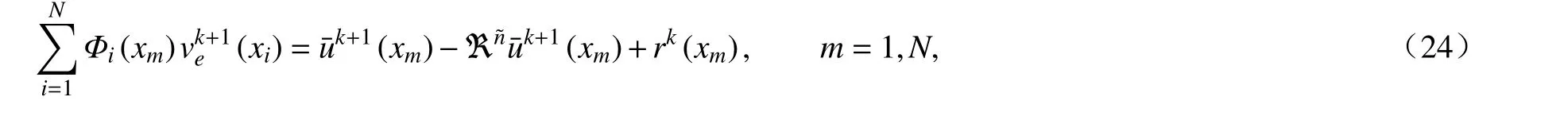
其中

式(21)和(24)可组装为如下矩阵形式：

3 数 值 算 例

考虑以下分数阶Cable 方程：

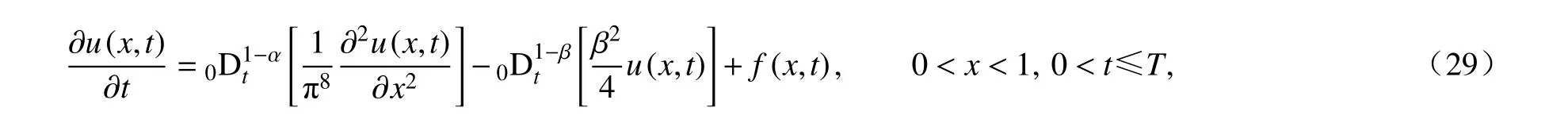
边界条件为

初始条件为

图1 给出了时间步长τ=1/20和节点间距h=1/20时，有限点法的数值解和误差.数据显示绝对误差小于3×10−4，说明解析解和数值解吻合得非常好，从而证明本文方法具有较高的计算精度.

图1 算例在α=0.2，β=0.8，T =5 ，h=1/20 和τ=1/20时的数值解和误差：(a) 数值解；(b) 误差Fig. 1 Numerical solution results and errors gained with α=0.2 , β=0.8, T =5 ，h=1/20 and τ=1/20: (a) numerical solution results; (b) errors

图2 给出了h=0.01时，相对误差//U−Uh//2///U//2和L∞误差与时间步长 τ之间的关系，图3 给出了当τ=0.000 1时，误差与节点间距h之间的关系.可以看出，误差随着τ和h的减小而减小，且数值解大约以τ1+min{α,β}和h2的速度收敛于解析解，这与理论结果一致.

图2 当h=0.01，T=1 时误差与时间步长τ的关系：(a) 相对误差；(b) L∞误差Fig. 2 The relationship between relative errors and L∞ errors obtained for h=0.01 and T=1 with respect to time-step size τ: (a) relative errors ; (b) L∞ errors

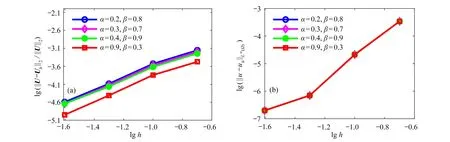
图3 当τ=0.000 1, T =1时误差与节点间距h的关系：(a) 相对误差；(b) L∞误差Fig. 3 The relationship between relative errors and L∞ errors obtained for τ=0.000 1 and T =1 with respect to nodal spacing h:(a) relative errors ; (b) L∞ errors

以上讨论的是α ≠β的情况，接下来讨论α=β=γ[8]的情况.图4 给出了τ=1/20和h=1/20时，有限点法的数值解和误差.图5(a)给出了h=0.01,T=1时，误差与τ之间的关系，图5(b)给出了当τ=0.000 1时，误差与h之间的关系.从图中可以看出有限点法获得了很好的数值结果.

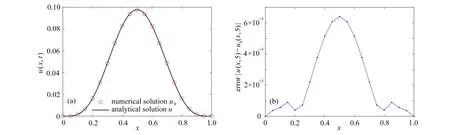
图4 算例在γ=0.4，T =5 ，h=1/20 和τ=1/20时的数值解和误差：(a) 数值解；(b) 误差Fig. 4 Numerical solution results and errors gained with γ=0.4, T =5 , h=1/20 and τ=1/20: (a) numerical solution results; (b) errors

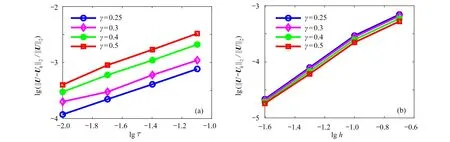
图5 误差与时间步长τ和节点间距h 的关系：(a) 时间步长τ；(b) 节点间距hFig. 5 The relationship between the errors and time-step size τ as well as nodal spacing h: (a) for time-step size τ; (b) for nodal spacing h

表1 比较了有限点法和径向基函数法[8]在h=0.1， γ=0.25和 γ=0.3时的L∞误差，我们发现有限点法具有更高的计算精度，明显优于径向基函数法.

表1 有限点法和径向基函数法在h=0.1, T =1时的 L∞误差Table 1 The L∞-errors of the finite point method and the radial basis function method gained with h=0.1, T =1

4 结 论

针对分数阶Cable 方程，本文用中心差分格式离散时间导数，用有限点法进行空间离散，推导了详细的数值计算公式，详细分析了该方法的误差估计.理论误差分析表明，数值解的误差与时间步长τ和节点间距h成正比，并且时间和空间收敛率分别约为τ1+min{α,β}和h2.数值算例证实了求解分数阶Cable 方程的有限点法的有效性和收敛性，并验证了理论分析结果.

参考文献（ References ） ：

［1］H U X L, ZHANG L M. Implicit compact difference schemes for the fractional Cable equation[J].Applied Mathematical Modelling, 2012, 36（9）: 4027-4043.

［2］L IAO H L, SUN Z Z. Maximum norm error estimates of efficient difference schemes for second-order wave equations[J].Journal of Computational and Applied Mathematics, 2010, 235（8）: 2217-2233.

［3］K HAN M A, ALI N H M, HAMID N N A. The design of new high-order group iterative method in the solution of two-dimensional fractional Cable equation[J].Alexandria Engineering Journal, 2021, 60（4）: 3553-3563.

［4］Q UINTANA-MURILLO J, YUSTE S B. An explicit numerical method for the fractional Cable equation[J].International Journal of Differential Equations, 2011, 72（2）: 447-466.

［5］Z HUANG P, LIU F, ANH V, et al. Stability and convergence of an implicit numerical method for the non-linear fractional reaction-subdiffusion process[J].IMA Journal of Applied Mathematics, 2005, 74: 645-667.

［6］A L-MASKARI M, KARAA S. The lumped mass FEM for a time-fractional Cable equation[J].Applied Numerical Mathematics, 2018, 132: 73-90.

［7］Z HENG R, LIU F, JIANG X, et al. Finite difference/spectral methods for the two-dimensional distributed-order time-fractional Cable equation[J].Computers & Mathematics With Applications, 2020, 80（6）: 1523-1537.

［8］D EHGHAN M, ABBASZADEH M, MOHEBBI A. Error estimate for the numerical solution of fractional reaction-subdiffusion process based on a meshless method[J].Journal of Computational and Applied Mathematics,2015, 280: 14-36.

［9］D EHGHAN M, ABBASZADEH M. Analysis of the element free Galerkin (EFG) method for solving fractional Cable equation with Dirichlet boundary condition[J].Applied Numerical Mathematics, 2016, 109: 208-234.

［10］C HENG Y M.Meshless Methods[M]. Beijing: Science Press, 2015.

［11］王 红, 李小林. 二维瞬态热传导问题的无单元Galerkin法分析[J]. 应用数学和力学, 2021, 42（5）: 460-469. （WANG Hong, LI Xiaolin. Analysis of 2D transient heat conduction problems with the element-free Galerkin method[J].Applied Mathematics and Mechanics, 2021, 42（5）: 460-469.（in Chinese））

［12］李 煜冬, 王发杰, 陈文. 瞬态热传导的奇异边界法及其MATLAB实现[J]. 应用数学和力学, 2019, 40（3）: 259-268. （LI Yudong, WANG Fajie, CHEN Wen. MATLAB implementation of a singular boundary method for transient heat conduction[J].Applied Mathematics and Mechanics, 2019, 40（3）: 259-268.（in Chinese））

［13］O ÑATE E, IDELSOHN S, ZIENKIEWICZ O C, et al. A finite point method in computational mechanics: applications to convective transport and fluid flow[J].International Journal for Numerical Methods in Engineering,1996, 39（22）: 3839-3866.

［14］O RTEGA E, FLORES R, OÑATE E, et al. A-posteriori error estimation for the finite point method with applications to compressible flow[J].Computational Mechanics, 2017, 60: 219-233.

［15］O ÑATE E, PERAZZO F, MIQUEL J. A finite point method for elasticity problems[J].Computers & Structures,2001, 79（22/25）: 2151-2163.

［16］L I X L, DONG H Y. Error analysis of the meshless finite point method[J].Applied Mathematics and Computation, 2020, 382: 125326.

［17］C HEN C M, LIU F, TURNER I, et al. A Fourier method for the fractional diffusion equation describing sub-diffusion[J].Journal of Computational Physics, 2007, 227（2）: 886-897.

［18］L I X L. Error estimates for the moving least-square approximation and the element-free Galerkin method inn-dimensional spaces[J].Applied Numerical Mathematics, 2016, 99: 77-97.

［19］B RENNER S C, SCOTT L R.The Mathematical Theory of Finite Element Methods[M]. New York: Springer,1994.