基于变体积约束的阻尼材料微结构拓扑优化研究*

张东东， 栾福强， 赵礼辉， 郑 玲

（1. 上海理工大学 机械工程学院，上海 200093；2. 上海市新能源汽车可靠性评价公共技术平台，上海 200093；3. 重庆大学 机械与运载工程学院，重庆 400044）

引 言

振动与噪声的控制水平是衡量航天飞行器、大型飞机、舰艇、高速列车等现代装备发展的重要技术指标.这些装备日益向高速、重载、轻质等方向发展，由此带来的振动与噪声问题更加突出.阻尼复合结构具有结构简单、减振降噪效果良好、可靠性高等优势，被广泛应用于各种大型装备薄壁结构的振动噪声控制，特别是对材料用量有苛刻要求的薄壁承载结构[1].

阻尼复合结构的减振性能取决于材料分布和材料属性.借助于拓扑优化方法，对阻尼复合材料的分布进行优化，可在控制材料用量的约束下达到高效减振降噪目的.Ansari 等[2]采用水平集法（level set method,LSM）对薄板结构表面约束阻尼材料的位置和形状进行寻优设计，并通过与试验结果对比验证了优化方法的有效性.Fang 等[3]以最小化谐振响应为目标函数，采用渐进优化方法（evolutionary structural optimization, ESO）寻找板结构表面约束阻尼材料的最优布局.Pang 等[4]以最大化加权模态损耗因子为目标对自由阻尼板结构进行了优化设计.在上述阻尼复合结构的宏观尺度拓扑优化中，一般都预先确定了阻尼材料的属性.

然而，材料属性对阻尼复合结构的减振降噪性能也有着重要影响，比如夹层阻尼结构主要依靠阻尼材料的横向剪切变形耗散振动能量，而且不同方向上剪切模量的差异还会引起抑振性能的变化.事实上，针对不同的抑振目标或工作环境，往往要求不同的阻尼材料属性，如夹层阻尼板梁结构不同阶抑振目标所要求的阻尼材料最优剪切模量都不相同[5].在工程应用中，不可能按照材料属性需求制造出所有相应的阻尼材料.此时，通过材料微观结构的优化设计获得期望的材料性能是一种非常有效实用的路径.

一方面，可以宏观结构的性能为目标设计材料微结构.Yang 等[6]以宏观结构的辐射声功率最小化为目标，对阻尼材料的微结构进行了优化设计.Chen 等[7]基于均匀化理论和实体各向同性材料惩罚（solid isotropic material with penalization, SIMP）插值方法设计了阻尼材料的微结构拓扑构型，旨在获得约束阻尼梁结构最大模态损耗因子.Fang 等[8]以约束阻尼结构模态损耗因子最大化为目标，基于能量法预测微结构的等效性能，设计了阻尼材料三维微结构拓扑构型.另一方面，则是直接以期望性能为目标开展阻尼材料的微结构设计.Chen 等[5]采用序列线性规划（sequential linear programming, SLP）方法研究了具有期望性能的阻尼材料微结构设计，并将其应用到约束阻尼梁结构.Andreasen 等[9]首先分析了在给定体积约束下的阻尼复合材料等效性能上下界，研究讨论了考虑制造性约束时阻尼材料微结构设计能否达到等效性能边界的问题.Huang 等[10]则以期望的材料损耗因子或弹性模量为目标，基于均匀化理论对阻尼复合材料的微结构进行了优化设计，将优化后阻尼材料的储能模量和耗能模量与Hashin 和Shtrikman[11-12]提出的理论界限（H-S 界限理论）进行了对比，结果表明以最大化刚度为目标优化设计得到的材料的储能模量接近H-S 理论的上限，以最大化阻尼为目标优化设计得到的材料的储能模量接近H-S 理论的下限.上述文献对阻尼材料微结构优化设计研究大都面向二维微结构问题，可以满足主要依靠拉压变形来耗散振动能量的自由阻尼结构的多尺度设计要求.但在工程实践中，具备更大减振降噪潜力的夹层阻尼复合结构，主要依靠阻尼材料横向剪切变形来耗散振动能量，那么，夹层阻尼复合结构的多尺度设计就需考虑阻尼材料的横向剪切模量.因此，将作为夹层的阻尼材料微结构优化设计定义为三维问题则是非常有必要的.另外，上述文献的优化过程都预先设定了阻尼材料的体积分数，并可获得预期材料性能，但对应的材料用量并非最少，难以保证充分利用材料.

复合材料有效模量的界限理论，如Voigt-Reuss 界限理论[13]和H-S[11-12]界限理论等，都是基于不同材料相的体积分数和本构参数构建多相复合材料等效性能极限的估计表达式，可用来指导材料微结构的设计.基于变分法的H-S 界限理论比较准确地描述了复合材料用量和等效模量界限的关系，应用较为广泛.为了实现最小材料用量获得期望的材料性能，本文将阻尼材料微结构等效为由实体材料和空材料构成的两相复合材料，基于H-S 界限理论提出一种变体积约束的阻尼材料微结构拓扑优化设计方法.基于均匀化理论，以阻尼材料期望的剪切模量为目标函数，构建了阻尼材料三维结构拓扑优化问题.通过逆用H-S 界限理论估计对应于期望等效剪切模量的材料体积分数限，并考虑到界限理论的精度局限性，提出了一种材料体积分数限移动准则，将原优化问题转化为体积约束下最大化等效模量的优化问题.采用最优准则法进行求解得到阻尼材料三维最优微结构，实现最小材料用量获得期望材料性能.通过典型数值算例验证了该方法的可行性和有效性，着重讨论了初始微构型、网格密度和弹性模量等对阻尼材料微结构的影响.

1 阻尼材料均匀化

1.1 阻尼材料复模量模型

那么，阻尼材料复数模量的张量形式可以重新表示为

1.2 阻尼材料均匀化方法

典型的夹层阻尼复合结构，如图1（a）所示，主要依靠黏弹性阻尼材料的横向剪切变形（图1（b））耗散能量实现减振降噪.图1 中的uc，uv，ub分别为约束层中性面、阻尼层中性面和基板层中性面沿x方向的位移，w为夹层阻尼复合结构的横向位移，ϕx为阻尼层绕y轴的转角，∂w/∂x为夹层阻尼复合结构绕x轴转动的角度.因此，对于夹层阻尼结构的阻尼材料微结构拓扑设计，需将其考虑为三维结构（图1（c））的优化设计问题.本文将阻尼材料单胞定义为正交各向异性材料，其本构关系为

图1 含阻尼材料微结构的夹层阻尼结构示意图：(a) 夹层阻尼结构；(b)阻尼材料变形图；(c)阻尼材料三维微结构Fig. 1 Schematic drawings of a sandwich damping structure with a damping core microstructure: (a) the sandwich damping structure;(b) the deformation of the damping core; (c) the 3D microstructure of the damping core

其中，σij和εkl为黏弹性材料的应力和应变张量.

均匀化理论是基于微观结构和材料组分来预测宏观结构性能的一种方法，它具有严格的数学理论基础，其性能预测结果更接近真实值[15].假设材料单胞尺寸远小于材料宏观结构尺寸，基于能量均匀化方法，阻尼材料单胞的等效复模量可以写为[16]

式中，vi表示虚拟位移场，属于可允许位移空间，yj表示微观尺度坐标系下的坐标.将式（1）代入式（5），则阻尼材料等效复模量可以写为

因此，基于单元的交互性能量，式（7）可转化为另一种新形式[17]：

本文中，周期性边界条件为给三维单胞边界施加约束方程，约束方程用周期性单胞顶点、边和面上的节点之间的位移差来表示[18].设阻尼材料单胞的微观单元材料是各向同性的，采用SIMP 插值模型函数来表示阻尼材料微观单元复模量的实部，则第e个微观单元刚度矩阵的实部为

2 变体积约束的阻尼材料微结构拓扑优化

2.1 传统拓扑优化模型

对于以期望等效材料性能为目标的阻尼材料微结构拓扑优化问题，通常可以表述为

2.2 变体积约束拓扑优化模型及求解

本文提出一种变体积约束的阻尼材料微结构拓扑优化设计方法.逆用H-S 界限理论估计对应于期望等效剪切模量的材料体积分数限，并考虑到界限理论的精度局限性，提出一种材料体积分数限移动准则，将传统优化问题转化为体积约束下最大化等效模量的优化问题.采用优化准则（optimal criterion，OC）法进行求解，得到阻尼材料三维最优微结构，实现最小材料用量获得期望材料性能.

2.2.1 目标函数

对于夹层阻尼结构，主要依靠阻尼材料的横向剪切变形来耗散能量.为最大化利用材料且充分挖掘阻尼材料的阻尼特性，将式（14）表达的拓扑优化问题转化为体积约束下最大化等效模量的优化问题.这里的体积约束限在下一小节由H-S 界限理论公式给出，是理论上获得期望等效模量的体积约束限.本文中最大化目标函数取为阻尼材料微结构单胞三个方向剪切模量的平均值，表示如下：

2.2.2 变体积约束

1) 初始体积约束限

如引言中所述，复合材料的界限理论描述了组分材料体积分数与等效性能极限之间的近似关系，应用较广泛的是H-S 界限理论.阻尼材料微结构可认为是由两相材料组成的复合材料，第一相为空材料，第二相为阻尼材料.那么，在给定阻尼材料体积下，基于H-S 界限理论公式可以预测阻尼材料微结构的等效剪切模量上限Gu为[11-12]

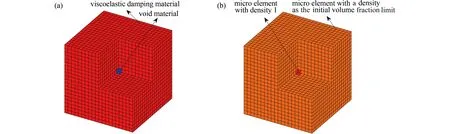
其中，G1，K1分别为空材料的剪切模量和体积模量，G2，K2分别为阻尼材料的剪切模量和体积模量，f1，f2分别为空材料和阻尼材料的体积分数.显然K1

本文旨在采用最小的材料用量获得具有期望等效性能的阻尼材料微结构.逆用H-S 界限理论，获得期望等效性能对应的阻尼材料体积限，这个体积即为理想情况下获得期望等效材料性能的最小体积.设Gexp为已知的期望阻尼材料剪切模量，则由方程（16）可获得Gu=Gexp时空材料和阻尼材料的体积分数f1和f2之间的关系如式（17）所示：

设空材料和阻尼材料的体积分数之和为1，令f1= 1–f2时，则可得到阻尼材料期望等效性能对应的阻尼材料体积分数限：

由于H-S 界限理论是一个理想理论，那么由式（18）的材料体积分数计算得到的最大剪切模量与期望剪切模量可能存在一定的误差.因此，本文进一步提出变体积约束限移动准则，保证优化后的阻尼材料微结构的等效剪切模量尽可能达到期望的剪切模量.将式（18）得到的阻尼材料初始体积分数f2记为所提出优化问题中的阻尼材料初始体积分数约束限f(0).

2) 体积约束限的移动准则

本文中的初始体积约束限为f(0)，在迭代过程中通过改变阻尼材料的体积分数约束限使优化后阻尼材料单胞的等效剪切模量达到期望的剪切模量.材料体积分数约束限f(k)的迭代格式可表示为

2.2.3 变体积约束拓扑优化模型及求解

以等效弹性模量构造目标函数是材料微结构设计中广泛采用的一种方法，尤其是以材料等效剪切模量构造目标函数，可使优化过程具有非常高的稳健性.基于SIMP 插值方法，以式（15）为目标函数、材料的移动体积分数限为约束进行材料微结构优化设计，提出变体积约束的阻尼材料微结构拓扑优化模型如下：

式中，f(k)是由式（19）定义的在第k迭代步的阻尼材料体积分数约束限.采用直接求导法得到目标函数和约束条件对变量的灵敏度后，通过优化准则法对该优化问题进行求解.为了保证微结构的连续性，采用灵敏度过滤技术消除棋盘格式[19].

3 数值算例与分析

笔者基于上述所提出的方法编制了变体积约束的阻尼材料微结构拓扑优化程序.阻尼材料三维微结构的初始构型如图2 所示，为方便描述，将其命名为初始构型A.将其离散为20 × 20 × 20 个有限元单元，每个单元的尺寸为0.05 mm × 0.05 mm × 0.05 mm，8 个角点单元为空材料（密度变量等于0），其余单元为实体阻尼材料单元（密度变量等于1）.实体阻尼材料采用复常数模量模型，弹性模量Ev为12 MPa、Poisson 比为0.48、材料损耗因子为0.5.

图2 阻尼材料单胞初始构型AFig. 2 Initial configuration A of the damping material unit cell

考虑阻尼材料微结构单胞的期望剪切模量Gexp分别为1 MPa，2 MPa 和3 MPa，那么由式（18）可得对应于3 个期望剪切模量的阻尼材料体积分数约束值分别为0.360，0.624 和0.830.此时为了获得3 种期望的剪切模量值，阻尼材料微结构的拓扑优化设计问题就转化为理想情况下在体积约束分别为0.360，0.624 和0.830 下的剪切模量最大化问题，目标函数如式（15）所示.在优化过程中，为了与求解最小化问题的优化算法相适应，将目标函数修改为最小化问题.

对于上述3 个不同的期望剪切模量，优化后的阻尼材料微结构拓扑构型、迭代历程以及等效剪切模量如图3 所示.优化后的阻尼材料微结构仍呈轴对称特征，迭代过程中阻尼材料的体积分数限呈现出移动变化的特征.对应的等效剪切模量分别为1.02 MPa，2.04 MPa 和3.04 MPa，非常接近期望剪切模量且误差都能控制在2%以内.优化后阻尼材料的体积分数分别为0.395，0.614 和0.830，与逆用H-S 界限理论得到的阻尼材料体积分数限相比，分别增加了9.73%，−1.61%，0%，与初始的材料体积分数限有一定的差异.这是由于H-S 界限理论本身是一种理想的近似理论，那么逆用H-S 界限理论获得的对应于期望等效剪切模量的材料体积分数限也是一个理想的估计值，必然存在一定的精度局限.因此，本文构造了材料体积分数限移动准则，在优化过程中通过增大或者减小材料的体积分数约束限来获得最小材料用量下具有期望剪切模量的阻尼材料微结构构型，实现材料的充分利用.

图3 基于初始构型A 获得阻尼材料单胞微结构拓扑优化结果Fig. 3 Topology optimization results of the damping material unit cell microstructure for initial configuration A

3.1 优化结果对初始构型的依赖性分析

在阻尼材料微结构单胞尺寸和网格密度不变的情况下，改变阻尼材料单胞的初始构型，分析它们对优化结果的影响.定义了两种不同的初始构型B 和C，如图4 所示.初始构型B 的中心8 个单元为空材料，其余单元为实体阻尼材料；初始构型C 的中心8 个单元为实体阻尼材料，其余单元为密度等于初始体积分数限值的阻尼材料.

图4 阻尼材料初始构型：(a) 阻尼材料初始构型B； (b) 阻尼材料初始构型CFig. 4 The initial configurations of the damping material unit cell：(a) initial configuration B of the damping material unit cell;(b) initial configuration C of the damping material unit cell

基于初始构型B 的阻尼材料微结构最优拓扑构型及等效剪切模量如图5 所示.优化后的阻尼材料微结构仍呈轴对称特征，对应的等效剪切模量分别为1.03 MPa，2.04 MPa 和3.04 MPa，可以认为达到了期望的剪切模量.优化后阻尼材料的体积分数分别为0.385，0.620 和0.828，与逆用H-S 界限理论得到的阻尼材料体积分数限相比，分别增加了6.95%，−0.60%，−0.24%.

图5 基于初始构型B 获得阻尼材料单胞微结构拓扑优化结果Fig. 5 Topology optimization results of the damping material unit cell microstructure for initial configuration B

基于初始构型C 的阻尼材料微结构最优拓扑构型及剪切模量如图6 所示.优化规整后的等效剪切模量分别为1.03 MPa，2.05 MPa 和3.05 MPa，与期望的剪切模量相比，误差控制在3%以内，仍可认为达到了期望的剪切模量.优化后阻尼材料的体积分数分别为0.388，0.604 和0.820，分别增加了7.78%，−3.20%，−1.2%.

图6 基于初始构型C 获得阻尼材料单胞微结构拓扑优化结果Fig. 6 Topology optimization results of the damping material unit cell microstructure for initial configuration C

分析上述优化结果可以看出：在不同的初始构型下，都可获得具有期望剪切模量的阻尼材料微结构，且材料用量（微结构体积分数）差别不大，但优化构型存在差异.本文采用相似度描述优化构型的差异性，定义为：不同初始构型的优化构型与参考构型的单元重合数量之比[20].以初始构型A 对应的优化构型（如图3 所示）为

参考构型，可获得初始构型B 下3 个优化构型的相似度分别为0.162，0.475 和0.794；初始构型C 下3 个优化构型的相似度分别为0.830，0.917 和0.968.因此，可以认为以初始构型B 获得的优化构型与初始构型A 差异大；以初始构型C 获得的优化构型与初始构型A 相似度高.

3.2 优化结果对网格密度的依赖性

讨论了阻尼材料单胞的网格密度对优化结果的影响.以初始构型A 为例，修改阻尼材料单胞网格密度分别为15 × 15 × 15，25 × 25 × 25 和30 × 30 × 30，对应的优化结果如图7～9 所示.

图7 单胞初始构型A 优化结果(15 × 15 × 15)Fig. 7 Topology optimization results of initial configuration A (15 × 15 × 15)

通过对比分析可以发现：①不同的网格密度下获得的阻尼材料单胞等效剪切模量与期望剪切模量的误差都在3%以内；②与逆用H-S 界限理论得到的阻尼材料理想体积分数相比，在期望剪切模量较小时（1 MPa），不同的网格密度下阻尼材料体积分数略微增加，其余两种期望剪切模量下的阻尼材料体积分数则变化很小；③不同的网格密度下，相对于阻尼材料的微结构最优构型具有相似的的材料分布特征，且随着网格数量的增加，微结构最优构型越光滑.

3.3 优化结果对材料弹性模量的依赖性分析

基于初始构型A，阻尼材料微结构的网格密度为20 × 20 × 20，每个微观单元的尺寸为0.05 mm × 0.05 mm ×0.05 mm .阻尼材料的Poisson 比和损耗因子分别为0.48 和0.5，阻尼材料的弹性模量分别选取10 MPa 和15 MPa.

阻尼材料的弹性模量为10 MPa 时，由式（18）可得对应于3 个期望剪切模量的阻尼材料体积分数约束值分别为0.417，0.712 和0.931.优化后的阻尼材料微结构构型及等效剪切模量如图10 所示.对应的等效剪切模量分别为1.01 MPa，2.03 MPa 和3.01 MPa，可以认为达到了期望的剪切模量；优化后阻尼材料的体积分数分别为0.436，0.701 和0.929，与逆用H-S 界限理论得到的阻尼材料体积分数限相比，分别增加了4.36%，−1.57%，−0.22%.

图9 单胞初始构型A 优化结果(30 × 30 × 30)Fig. 9 Topology optimization results of initial configuration A (30 × 30 × 30)

图10 基于初始构型A 的拓扑优化结果(Ev=10 MPa)Fig. 10 Topology optimization results of initial configuration A (Ev=10 MPa)

阻尼材料的弹性模量为15 MPa 时，对应于3 个期望剪切模量的阻尼材料体积分数约束值分别为0.295，0.526 和0.712.优化后的阻尼材料微结构构型及等效剪切模量如图11 所示.对应的等效剪切模量分别为1.02 MPa，2.04 MPa 和3.03 MPa，与期望的剪切模量相比，误差控制在2%以内，仍可认为达到了期望的剪切模量；优化后阻尼材料的体积分数分别为0.333，0.531 和0.699，与逆用H-S 界限理论得到的阻尼材料体积分数限相比，分别增加了11.41%，−0.94%，−1.86%.

对比不同弹性模量下阻尼材料的优化结果，可以看出：阻尼材料的弹性模量变化时，仍可获得具有期望剪切模量的微结构；当期望的剪切模量相同时，阻尼材料弹性模量越大，优化后的阻尼材料微结构体积分数越小.

4 结 论

本文以最小材料用量获得期望阻尼材料特性为目标，提出了基于变体积约束的阻尼材料微结构拓扑优化设计方法.以获得阻尼材料的期望剪切模量为目标，逆用H-S 界限理论估计对应于期望等效剪切模量的材料体积分数限，并提出体积分数约束限的移动准则，将阻尼材料微结构拓扑优化问题转化为材料体积约束下的阻尼材料剪切模量最大化拓扑优化问题.通过数值算例，得出了以下结论：

1) 该方法可以很好地实现在最小材料用量下获得具有期望性能的阻尼材料微结构；

2) 优化后阻尼材料微结构的拓扑构型受初始构型的影响较大，但基于不同初始构型优化后的阻尼材料微结构体积分数差别不大；

3) 优化后阻尼材料微结构的拓扑构型和体积分数对阻尼材料单胞网格密度的依赖性很小，且优化后的拓扑构型随着网格密度的增加而变得光滑；

4）优化后阻尼材料微结构的拓扑构型对弹性模量的依赖性较小，阻尼材料弹性模量越大，优化后的阻尼材料微结构体积分数越小.

参考文献（ References ） ：

［1］曾 昭阳, 范红伟, 焦映厚, 等. 基于三明治夹层约束阻尼结构的潜艇降噪[J]. 科学技术与工程, 2020, 20（22）: 8975-8982. （ZENG Zhaoyang, FANG Hongwei, JIAO Yinghou, et al. Noise reduction of submarine based on sandwich constrained layer damping structure[J].Science Technology and Engineering, 2020, 20（22）: 8975-8982.（in Chinese））

［2］A NSARI M, KHAJEPOUR A, ESMAILZADEH E. Application of level set method to optimal vibration control of plate structures[J].Journal of Sound and Vibration, 2013, 332（4）: 687-700.

［3］F ANG Z P, ZHENG L. Topology optimization for minimizing the resonant response of plates with constrained layer damping treatment[J].Shock and Vibration, 2015, 2015（2）: 1-11.

［4］P ANG J, ZHENG W G, YANG L, et al. Topology optimization of free damping treatments on plates using level set method[J].Shock and Vibration, 2020, 2020: 5084167.

［5］C HEN W J, LIU S T. Topology optimization of microstructures of viscoelastic damping materials for a prescribed shear modulus[J].Structural and Multidisciplinary Optimization, 2014, 50（2）: 287-296.

［6］Y ANG R Z, DU J B. Microstructural topology optimization with respect to sound power radiation[J].Structural and Multidisciplinary Optimization, 2013, 47（2）: 191-206.

［7］C HEN W J, LIU S T. Microstructural topology optimization of viscoelastic materials for maximum modal loss factor of macrostructures[J].Structural and Multidisciplinary Optimization, 2016, 53（1）: 1-14.

［8］F ANG Z P, LEI Y, TIAN S X, et al. Microstructural topology optimization of constrained layer damping on plates for maximum modal loss factor of macrostructures[J].Shock and Vibration, 2020, 2020: 8837610.

［9］A NDREASEN C S, ANDREASSEN E, JENSEN J S, et al. On the realization of the bulk modulus bounds for two-phase viscoelastic composites[J].Journal of the Mechanics and Physics of Solids, 2014, 63（1）: 228-241.

［10］H UANG X D, ZHOU S W, SUN G Y, et al. Topology optimization for microstructures of viscoelastic composite materials[J].Computer Methods in Applied Mechanics and Engineering, 2015, 283: 503-516.

［11］H ASHIN Z, SHTRIKMAN S. A variational approach to the theory of the elastic behaviour of multiphase materials[J].Journal of the Mechanics and Physics of Solids, 1963, 11（2）: 127-140.

［12］H ASHIN Z. Complex moduli of viscoelastic composites, Ⅰ: general theory and application to particulate composites[J].International Journal of Solids and Structures, 1970, 6（5）: 539-552.

［13］杨 大鹏, 刘新田. 复合材料有效弹性模量的上、下限的求解[J]. 郑州大学学报(工学版), 2002, 23（2）: 106-109.（YANG Dapeng, LIU Xintian. Solution to the upper and lower bounds of the effective elastic modulus of composite materials[J].Journal of Zhengzhou University(Engineering Edition), 2002, 23（2）: 106-109.（in Chinese））

［14］L IU Q M, RUAN D, HUANG X. Topology optimization of viscoelastic materials on damping and frequency of macrostructures[J].Computer Methods in Applied Mechanics and Engineering, 2018, 337: 305-323.

［15］程 可朋, 王宪杰, 张洵安, 等. 周期性复合材料构型及结构一体化优化[J]. 应用数学和力学, 2015, 36（7）: 725-732.（CHENG Kepeng, WANG Xianjie, ZHANG Xun’an, et al. Collaborative optimization of structures with periodic composite materials[J].Applied Mathematics and Mechanics, 2015, 36（7）: 725-732.（in Chinese））

［16］S IGMUND O. Materials with prescribed constitutive parameters: an inverse homogenization problem[J].International Journal of Solids and Structures, 1994, 31（17）: 2313-2329.

［17］X IA L, BREITKOPF P. Design of materials using topology optimization and energy-based homogenization approach in Matlab[J].Structural and Multidisciplinary Optimization, 2015, 52（6）: 1229-1241.

［18］G AO J, LI H, GAO L, et al. Topological shape optimization of 3D micro-structured materials using energy-based homogenization method[J].Advances in Engineering Software, 2018, 116: 89-102.

［19］S IGMUND O. Morphology-based black and white filters for topology optimization[J].Structural and Multidisciplinary Optimization, 2007, 33（4）: 401-424.

［20］Z HANG D D, WU Y H, LU X, et al. Topology optimization of constrained layer damping plates with frequencyand temperature-dependent viscoelastic core via parametric level set method[J].Mechanics of Advanced Materials and Structures, 2021, 29（1）: 154-170.