X 构型张力非线性系统共振激励下的拍振现象*

齐子涵， 吴志强， 焦云雷， 贾文文

（1. 天津大学 力学系，天津 300350；2. 天津航天机电设备研究所，天津 300458；3. 中国空间技术研究院 总体部，北京 100094）

引 言

随着我国航天事业的发展，圆形太阳翼因高功率质量比、结构紧凑等特点逐渐替代矩形太阳翼，引起了人们的重视[1].张力机构是圆形太阳翼能够保持太阳毯张紧的关键机构，通常由两侧的绳和弹簧组成接近X 形的构型，其力学特性具有明显的非线性特征.由于制造及安装误差等原因，张力机构连接的太阳翼两部分可能不是严格对称的.因而，分析张力非线性对系统动力学的影响时，需要考虑这种结构不对称的影响.但是由于此机构存在张力非线性因素，当两肋板出现不对称情况时，在张力非线性的作用下将会出现拍振.因此，研究其不同激励条件下的拍振对于实施拍振控制有重要作用.

拍振现象可见于各类工程实例中，因而得到人们的重视.温登哲等[2]总结了航空发动机双转子系统动力学发展，并强调了拍振对双转子系统的影响；陈茉莉等[3]指出多维图形法在多源拍振中的小频差识别应用；廖明夫等[4]在研究双转子系统时发现，转子转差率很小时拍振现象十分明显；韩军等[5]分析了拍振周期性和信号强度及反向转子的基本特性，对产生拍振的双转子系统的特征进行了较好的阐述；Zeng 等[6]通过解拍的方法对双转子不平衡振动进行信号提取；高天[7]对双转子系统阵发性冲击振动采用了Hilbert 包络谱的分析方法，清晰地提取了系统中的周期损伤频率及其倍频.在桥梁方面，Caetano 等[8]通过对Guadiana 桥进行现场测试，观测到不同模态间的内共振及斜拉索拍振.在此基础上，孙测世等[9]分析了单频激励能激发斜拉索拍振的原因.Park 等[10]对怠速拍振与车辆振动的关系进行了探究，为车辆设计提供了指导.朱剑涛等[11]采用Fourier 变换、冲击响应谱和小波分析方法分析了星箭组合体的拍振特点，为后续卫星状态的确定提供了参考依据；练继建等[12]对泄洪激励下二滩拱坝拍振现象的机理进行研究，分析了拱坝拍振的主要原因；Zhang 等[13]分析了电介质弹性体膜电压诱发拍振的机理；Endo 等[14]对大型浮式结构的拍振现象进行分析，指导了海洋平台的设计；Kim 等[15-16]利用脉冲响应研究了不对称环、钟的拍频分布特征；高辉等[17]通过研究主动磁悬浮轴承系统拍振现象，提出控制磁悬浮轴承广义动刚度的方法以降低拍振的影响.在工程实例中，拍振多是以时域和频谱进行分析，并且更多地是对拍振出现的原因进行探究，未阐述系统非线性响应与拍振的关系.

本文基于张力机构特点，使用Lagrange 能量法进行两肋板结构尺寸非对称情况建模，对激励幅值改变的对称激励下系统非线性动力学响应进行求解，分析了结构拍振的原因，通过计算系统典型响应并结合时域、Poincaré截面、频谱以及Hilbert 包络谱等手段，探究了系统不同非线性响应状态与拍振具体形式的关系.

1 带有张力非线性系统的动力学模型

1.1 系统结构

如图1 所示，系统由两个静平衡状态间距为L的悬臂型肋板组成，两个板间通过张力调节单元连接，外侧均与接地弹簧k1相连.固定端有位移激励Ui(t)=Yicos(ωt)，wi(x,t)表示第i个肋板固定端所受位移激励及板振动变形.

图1 张力非线性结构模型示意图Fig. 1 Schematic diagram of the tension nonlinear symmetric model

1.2 系统动力学方程推导

由于肋板变形小，且以一阶为主，故可假设肋板i(i= 1, 2 )的振动位移为

其中Φ(x)为悬臂梁一阶模态函数. 将以上方程代入到非保守系统的Lagrange 方程

可得两自由度非线性方程：

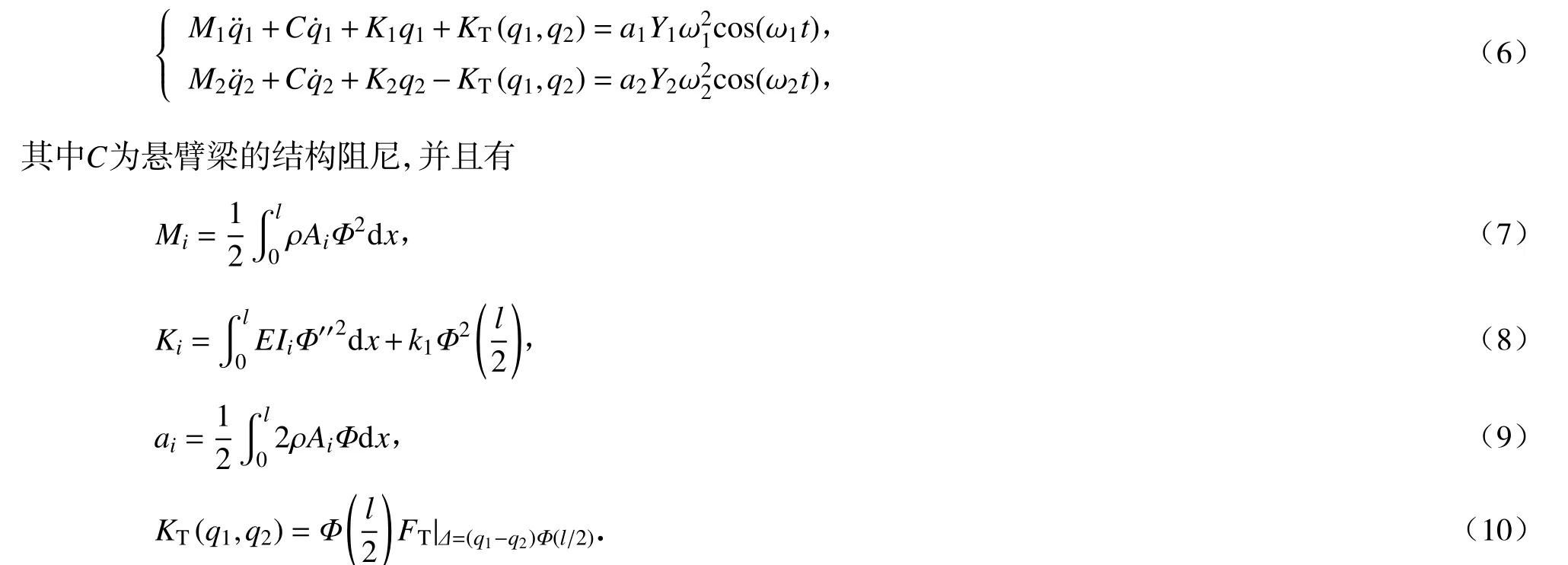
1.3 方程无量纲化

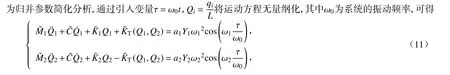
表1 模型参数取值Table 1 Values of model parameters

2 拍振现象原因分析

以激励幅值0.3，激励频率1 时的强迫共振响应为例，通过比较线性、非线性响应，分析拍振产生的原因.图2 为线性系统响应，图3 为非线性系统响应.

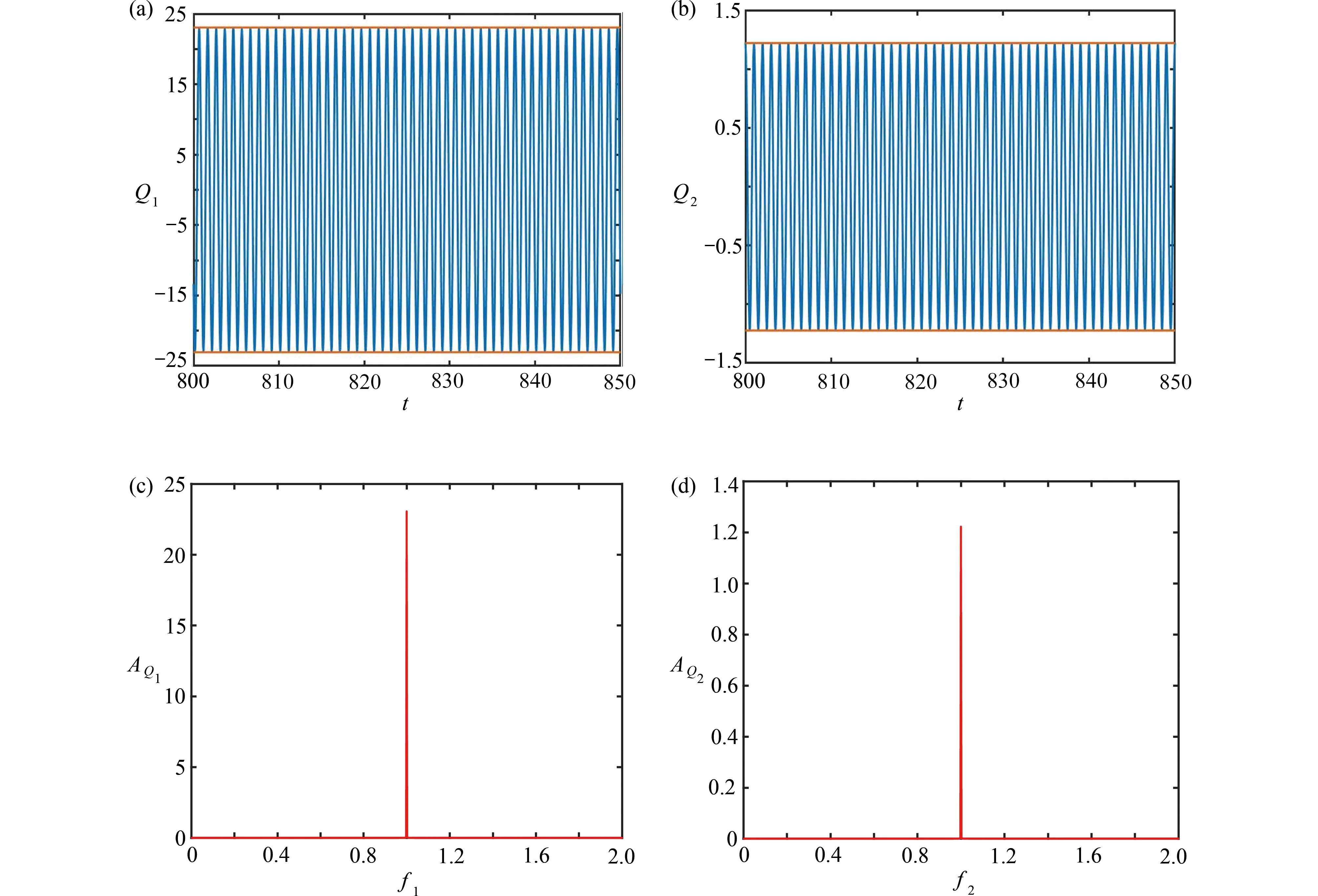
图2 激励幅值为0.3 线性系统的响应：(a) 肋板1 时间历程图；(b) 肋板2 时间历程图；(c) 肋板1 频谱图；(d) 肋板2 频谱图Fig. 2 With an excitation amplitude of 0.3, the linear system responses：(a) the time history diagram of rib 1; (b) the time history diagram of rib 2;(c) the spectrum diagram of rib 1; (d) the spectrum diagram of rib 2

图3 激励幅值为0.3 非线性系统的响应：(a) 肋板1 时间历程图；(b) 肋板2 时间历程图；(c) 肋板1 Poincaré截面图；(d) 肋板2 Poincaré截面图；(e) 肋板1 频谱图；(f) 肋板2 频谱图；(g) 肋板1 Hilbert 包络谱；(h) 肋板2 Hilbert 包络谱Fig. 3 With an excitation amplitude of 0.3, the nonlinear system responses: (a) the time history diagram of rib 1; (b) the time history diagram of rib 2;(c) the Poincaré section diagram of rib 1; (d) the Poincaré section diagram of rib 2; (e) the spectrum diagram of rib 1; (f) the spectrum diagram of rib 2; (g) the Hilbert envelope spectrum diagram of rib 1; (h) the Hilbert envelope spectrum diagram of rib 2

线性系统响应中，由于两肋板截面尺寸不同，导致肋板1 固有频率为1，肋板2 固有频率略低于1，因此图2线性系统由于共振使肋板1 位移极值远大于肋板2，但在时域图像中都未出现拍振现象，说明带有张力非线性的非对称系统在对称激励下的拍振现象并非是由结构固有频率的差异引起的.

张力非线性系统在相同激励条件下的响应如图3 所示.因所讨论的系统受周期激励作用，其Poincaré截面图由稳态响应时间历程间隔激励周期取点后绘制的相图得到.与线性情况不同的是，两肋板位移极值相近且出现拍振现象.综合图2 分析可知，此结构拍振是由具有张力非线性的张力调节单元耦合作用引起的.

3 非对称系统分岔分析

本节通过计算Poincaré映射分岔，获得激励幅值较大范围变化时响应的变化情况，之后选择典型参数分析拍振现象.

激励幅值从0 到3 变化时系统分岔见图4.激励幅值在0 ～ 0.28，1.67 ～ 1.74，1.99 ～ 2.03，2.15 ～ 2.5 以及2.67 ～ 3 五个范围时响应属于简单周期运动，暂不讨论.而激励幅值处于其他范围时系统响应会出现概周期运动乃至混沌运动.具体运动形式判定，下文将从时间历程、Poincaré截面图、频谱和Hilbert 包络谱的角度进行分析.限于篇幅，这里给出激励幅值Y为0.3，0.67，0.72 和2.66 时的结果.

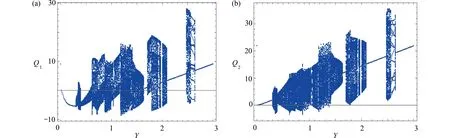
图4 激励幅值改变下肋板分岔图：(a) 肋板1 分岔图；(b) 肋板2 分岔图Fig. 4 With a changing excitation amplitude, the bifurcation diagrams of the lower ribs: (a) the bifurcation diagram of rib 1; (b) the bifurcation diagram of rib 2

图3 为激励幅值为0.3 时的系统响应，此处不再重复.从时间历程来看，虽然两个肋板的最大振幅均为6 左右，但其拍振波形有明显不同，肋板2 存在大小拍现象.Poincaré截面图说明运动是概周期的，但肋板1、2 分别为单环和三环.频谱图显示，在主振动频率1 附近出现多个频率，这些很接近的频率正是导致结构拍振的主要原因.通过图3(g)、(h) 的Hilbert 包络谱，可以清晰地得到拍振特点：两个肋板都是由两小拍组成一大拍，小拍频率为0.08，对应拍振周期为12.5，大拍频率为0.04，对应拍振周期为25，这两个频率分别对应Hilbert 包络谱中的第一、第二两个频率.两个肋板拍振具体形式略有差别，主要体现在Hilbert 包络谱中频率为0.08 的幅值不同：肋板1 两小拍不明显，几乎合为一拍，因此0.08 频率幅值很小；肋板2 两小拍清晰，因此0.08 频率幅值与0.04 幅值相近.

图5 为激励幅值为0.67 时的系统响应.时间历程图中的振动幅值都有所增加，两个肋板大小拍更加明显.系统的Poincaré截面显示运动仍是概周期的，但是出现了更高程度的折叠.频谱图中，频率数量增加使拍振现象更为复杂.而通过图5(g)、(h) 的Hilbert 包络谱可以清晰地看出，拍振的频率呈倍频形式出现，表明此拍振现象是以多个周期相同的拍振周期组成，而其中最小拍振频率0.0235，对应拍振最大周期42.对肋板1 来说，最大拍振周期内存在7 个小周期，因此幅值最大的频率为对应最大周期的频率0.0235 和0.0235 的7 倍频；对肋板2 来说，最大拍振周期内存在3 个小周期，因此幅值最大的频率是0.0235 和0.0235 的3 倍频.同时，由于肋板2 一个大周期内的三个小周期幅值比较接近，使其包络线周期明显，因此0.0235 的三倍频幅值最大.Hilbert 包络谱中，还存在一些更高倍数的频率，这些频率的出现主要是因为在每一小拍中并非是均匀严格的拍振形式，其最大振幅的波动使Hilbert 包络谱中出现更小的周期.这些倍频说明，拍振最大周期42 同样是幅值波动周期的整数倍.

图5 激励幅值为0.67 结构非对称系统的响应：(a) 肋板1 时间历程图；(b) 肋板2 时间历程图；(c) 肋板1 Poincaré截面图；(d) 肋板2 Poincaré截面图；(e)肋板1 频谱图；(f) 肋板2 频谱图；(g) 肋板1 Hilbert 包络谱；(h) 肋板2 Hilbert 包络谱Fig. 5 With an excitation amplitude of 0.67, the asymmetric-structure system responses: (a) the time history diagram of rib 1; (b) the time history diagram of rib 2; (c) the Poincaré section diagram of rib 1; (d) the Poincaré section diagram of rib 2; (e) the spectrum diagram of rib 1; (f) the spectrum diagram of rib 2; (g) the Hilbert envelope spectrum diagram of rib 1; (h) the Hilbert envelope spectrum diagram of rib 2

当系统的激励幅值增加到0.72 时，系统响应如图6 所示.从时间历程来看，响应仍具有拍的特征，但拍已不具备周期性.由图6(c)、(d)可以看出，系统已处于混沌状态，Poincaré截面中成片的点状区域是在图5(c)、(d)Poincaré截面闭合曲线形状基础上形成的.由此，可初步推断该混沌行为是激励幅值Y=0.67 时的概周期解经过环面分岔而形成.从Hilbert 包络谱上看到存在0.035 和0.07，对应周期为14.28 和28.57 的拍振现象，而肋板1 的响应中存在很多小拍，是因其Hilbert 包络谱中还有更高频的主要成分.

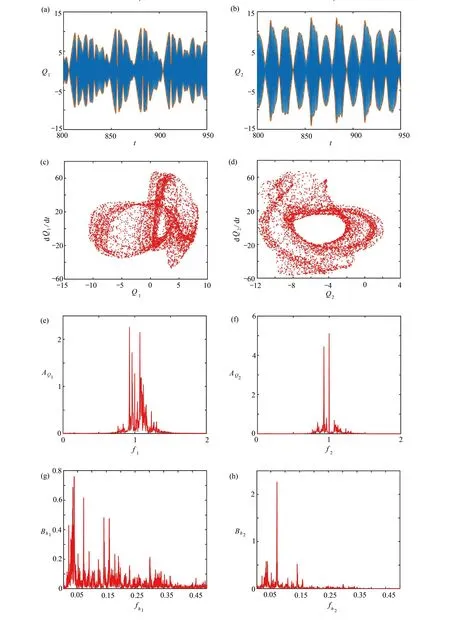
图6 激励幅值为0.72 结构非对称系统的响应：(a) 肋板1 时间历程图；(b) 肋板2 时间历程图；(c) 肋板1 Poincaré截面图；(d) 肋板2 Poincaré截面图；(e)肋板1 频谱图；(f) 肋板2 频谱图；(g) 肋板1 Hilbert 包络谱；(h) 肋板2 Hilbert 包络谱Fig. 6 With an excitation amplitude of 0.72, the asymmetric-structure system responses: (a) the time history diagram of rib 1; (b) the time history diagram of rib 2; (c) the Poincaré section diagram of rib 1; (d) the Poincaré section diagram of rib 2; (e) the spectrum diagram of rib 1; (f) the spectrum diagram of rib 2; (g) the Hilbert envelope spectrum diagram of rib 1; (h) the Hilbert envelope spectrum diagram of rib 2

激励幅值继续增加，系统响应经历从混沌到概周期，再到周期的多次转换，特别是在激励幅值Y为2.59 到2.68 时，呈现复杂周期现象.图7 给出了Y=2.66 时的计算结果.时间历程拍振现象明显，周期性较强.Poincaré截面出现了接近点状的多点分布图形，说明拍振基频与主振频率之间接近倍数关系.由图7(g)可知拍振基频为0.0625，与主振频率的比值为16，与Poincaré截面图中的点数相同.与其他响应情况相比，复杂周期响应的拍振频率略高，说明拍振周期更小，以五个小拍为一个大拍周期.

图7 激励幅值为2.66 结构非对称系统的响应：(a) 肋板1 时间历程图；(b) 肋板2 时间历程图；(c) 肋板1 Poincaré截面图；(d) 肋板2 Poincaré截面图；(e) 肋板1 频谱图；(f) 肋板2 频谱图；(g) 肋板1 Hilbert 包络谱；(h) 肋板2 Hilbert 包络谱Fig. 7 With an excitation amplitude of 2.66, the asymmetric-structure system responses: (a) the time history diagram of rib 1; (b) the time history diagram of rib 2; (c) the Poincaré section diagram of rib 1; (d) the Poincaré section diagram of rib 2; (e) the spectrum diagram of rib 1; (f) the spectrum diagram of rib 2; (g) the Hilbert envelope spectrum diagram of rib 1; (h) the Hilbert envelope spectrum diagram of rib 2

4 结 论

圆形太阳翼中包含了一种特殊的张力单元以调节其内部张力，该单元由绳和弹簧组合成为X 形构型，其力学特性具有强非线性特征.为研究此类张力单元的影响，本文给出了包含张力单元的双悬臂梁力学机理模型，导出了其动力学方程，通过频谱、Hilbert 包络谱和Poincaré截面等手段重点分析了系统中存在的拍振现象.

1) 拍振现象是由张力非线性引起，在位移激励和张力弹簧的作用下肋板的频谱图出现多个间隔相等的频率，而两肋板固有频率的区别使其出现特点不同的拍振现象.

2) 虽然两肋板受到激励相同，因其截面积不同导致其拍振行为有较大差别.拍振过程中肋板1 的幅值会有较大变化但不会变为零，而肋板2 的幅值通常会变小到零.

3) 激励幅值变化时，系统存在不同拍振行为，可能是概周期、多倍周期或混沌三种类型之一，并且都有大拍中套小拍的现象.

4) 对拍振行为，Hilbert 包络谱比频谱更直观，对概周期以及多倍周期的拍振现象，可由Hilbert 包络谱的基频得到响应波形变化的频率和周期，而基频与倍频成分对应谱线的相对高低，则与大拍中包含的小拍特征是否明显有关.

参考文献（ References ） ：

［1］周 志清, 吴跃民, 王举, 等. 圆形太阳翼发展现状及趋势[J]. 航天器工程, 2015, 24（6）: 116-122. （ZHOU Zhiqing,WU Yuemin, WANG Ju, et al. Development and trend of circular solar array[J].Spacecraft Engineering, 2015,24（6）: 116-122.（in Chinese））

［2］温 登哲, 陈予恕. 机动飞行时航空发动机的双转子动力学研究综述[C]//中国振动工程学会, 中国力学学会. 第十三届全国非线性振动暨第十届全国非线性动力学和运动稳定性学术会议摘要集. 2011: 6. （WEN Dengzhe, CHEN Yushu. A review of the research on two-rotor dynamics of aeroengines in maneuvering flight[C]//Chinese Society of Vibration Engineering, The Chinese Society of Theoretical and Applied Mechanics. Proceedings of the 10th International Conference on Nonlinear Dynamics and Motion Stability. 2011: 6. （in Chinese））

［3］陈 茉莉, 李舜酩, 温卫东, 等. 多源拍振分析方法与试验[J]. 振动、测试与诊断, 2011, 31（2）: 202-206, 267. （CHEN Moli, LI Shunming, WEN Weidong, et al. Analysis and experiment on multi-source beat vibration[J].Journal of Vibration,Measurement and Diagnosis, 2011, 31（2）: 202-206, 267.（in Chinese））

［4］廖 明夫, 于潇, 王四季, 等. 双转子系统的振动[J]. 机械科学与技术, 2013, 32（4）: 475-480. （LIAO Mingfu, YU Xiao,WANG Siji, et al. The vibration features of a twin spool rotor system[J].Mechanical Science and Technology forAerospace Engineering, 2013, 32（4）: 475-480.（in Chinese））

［5］韩 军, 高德平, 胡绚, 等. 航空发动机双转子系统的拍振分析[J]. 航空学报, 2007, 28（6）: 1369-1373. （HAN Jun,GAO Deping, HU Xuan, et al. Research on beat vibration of dual-rotor for aero-engine[J].Acta Aeronautica et Astronautica Sinica, 2007, 28（6）: 1369-1373.（in Chinese））

［6］Z ENG S, WANG X X. Unbalance identification and field balancing of dual rotors system with slightly different rotating speeds[J].Journal of Sound and Vibration, 1999, 220（2）: 343-351.

［7］高 天. 机动飞行环境下航空发动机转子系统瞬态动力学特性研究[D]. 博士学位论文. 天津: 天津大学, 2021. （GAO Tian. Research on transient dynamic characteristics of aeroengine rotor systems under maneuvering flight environment[D]. PhD Thesis. Tianjin: Tianjin University, 2021. （in Chinese））

［8］C AETANO E, CUNHA A, GATTULLI V, et al. Cable-deck dynamic interactions at the International Guadiana Bridge: onsite measurements and finite element modelling[J].Structural Control and Health Monitoring, 2008,15（3）: 237-264.

［9］孙 测世, 赵珧冰, 康厚军, 等. 斜拉桥的多重内共振及其耦合过程研究[J]. 振动与冲击, 2018, 37（10）: 87-93. （SUN Ceshi, ZHAO Yaobing, KANG Houjun, et al. Multiple internal resonances and coupling process of cable-stayed bridge[J].Journal of Vibration and Shock, 2018, 37（10）: 87-93.（in Chinese））

［10］P ARK J, LEE J, AHN S, et al. Reduced ride comfort caused by beating idle vibrations in passenger vehicles[J].International Journal of Industrial Ergonomics, 2017, 57: 74-79.

［11］朱 剑涛, 刘晨, 朱位, 等. 星箭组合体主动段飞行中拍频振动分析[C]//中国振动工程学会, 南京航空航天大学机械结构力学及控制国家重点实验室. 第十二届全国振动理论及应用学术会议论文集. 2017: 9. （ZHU Jiantao, LIU Chen,ZHU Wei, et al. Analysis of beat frequency vibration characteristics of active flight section of satellite-rocket combination[C]//Chinese Society of Vibration Engineering, State Key Laboratory of Mechanics and Control of Mechanical Structures, Nanjing University of Aeronautics and Astronautics.Proceedings of the 12th National Conference on Vibration Theory and Application. 2017: 9. （in Chinese））

［12］练 继建, 李成业, 刘昉, 等. 环境激励下二滩拱坝拍振机理的研究[J]. 振动与冲击, 2012, 31(3): 1-7. （LIAN Jijian, LI Chengye, LIU Fang, et al. Beat vibration of ertan arch dam under ambient excitation[J].Journal of Vibration and Shock, 2012, 31（3）: 1-7. （in Chinese））

［13］Z HANG Junshi, CHEN Hualing. Voltage-induced beating vibration of a dielectric elastomer membrane[J].Nonlinear Dynamics, 2020, 100: 2225-2239.

［14］E NDO H, SUZUKI H. Beating vibration phenomenon of a very large floating structure[J].Journal of Marine Science and Technology, 2018, 23（3）: 662-677.

［15］K IM S H, LEE C W, LEE J M. Beat characteristics and beat maps of the King Seong-Deok Divine Bell[J].Journal of Sound and Vibration, 2005, 281（1/2）: 21-44.

［16］K IM S H, SOETEL W, LEE J M. Analysis of the beating response of bell type structures[J].Journal of Environmental Research, 1994, 173（4）: 517-536.

［17］高 辉, 徐龙祥. 主动磁悬浮轴承系统拍振现象分析[J]. 机械工程学报, 2011, 47（13）: 104-112. （GAO Hui, XU Longxiang. Analysis of beat vibration for active magnetic bearing system[J].Journal of Mechanical Engineering,2011, 47（13）: 104-112.（in Chinese））