双侧弹性约束悬臂梁的非光滑擦边动力学*

史美娇， 徐慧东， 张建文

（1. 太原理工大学 数学学院，太原 030024；2. 太原理工大学 机械与运载工程学院，太原 030024）

引 言

梁作为工程中最常见的结构单元，广泛应用于航空航天、汽车、海洋工程、机械工程等领域.在应用设计时经常需要考虑这类结构在碰撞冲击作用下的承载能力，因此碰撞冲击作用下梁的动力学行为具有重要的研究价值.

反复持续碰撞的梁是一种典型的非光滑动力系统，系统中碰撞的非光滑因素会使系统发生一种特殊的擦边现象，即运动轨线以零速度与约束面接触.定性研究擦边动力学的常用工具是不连续映射方法，基于该方法得到的擦边规范形复合映射在一定程度上可以描述擦边点附近的动力学行为.Nordmark[1]首先引入了不连续映射的概念，为后续的许多研究奠定了基础.Chin 等[2]基于不连续映射方法揭示了三种余维一的擦边分岔行为.Lamba 和 Budd[3]调查了擦边分岔邻域内不连续映射的Lyapunov 指数，并揭示了最大Lyapunov 指数在擦边邻域内的跳跃现象.Fredriksson 和 Nordmark[4]推导了多自由度碰撞振动系统的局部零时间不连续映射的规范式，并确立了擦边分岔的稳定性准则.Li 等[5]和Xu 等[6]利用不连续映射方法研究了一般n自由度碰撞振动系统单擦边轨道和双擦边轨道附近的动力学行为，并给出了双擦边轨道的稳定性条件.以上文献都是基于低阶的擦边复合映射来调查擦边附近的动力学行为，然而低阶的规范形映射在某些特殊参数范围内无法真实反应原系统的擦边动力学.针对这个问题，Weger 等[7]和 Molenaar 等[8]修正了单自由度碰撞系统的低阶零时间不连续映射范式，并调查了修正项对擦边分岔行为的影响.Zhao[9]对一类单自由度刚性碰撞振子的Poincaré不连续映射(PDM)的范式作了修正，并通过数值仿真验证了范式的正确性.Yin 等[10]推导获得了一般碰撞系统的高阶零时间不连续映射，并基于高阶映射调查了擦边附近周期一运动的存在性，通过与低阶映射比较，验证了高阶不连续映射的有效性.据笔者所知，通过推导高阶的 PDM 分段映射来研究弹性碰撞系统的双擦边轨道附近的动力学行为尚未有报道.

本文以一类双侧弹性约束的单自由度悬臂梁为研究对象，调查了双擦边周期运动的存在性，推导了双擦边周期运动附近带参数的高阶 PDM 分段映射，并结合光滑流映射获得了新的复合范式映射，通过数值仿真对低阶映射和高阶映射反应的擦边分岔进行比较，验证了高阶范式映射的有效性，并揭示了双边弹性碰撞悬臂梁 的擦边动力学.

1 系统模型及其动力学方程

图1 为具有双侧弹性约束的悬臂梁系统，系统的质量主要集中在悬臂梁的自由端，用质量为的圆形质块M来表示，悬臂梁的长度为l，取M静平衡位置为坐标原点，质块M受到简谐激振力的作用作竖直方向的运动.上下约束分别由刚度为和的线性弹簧构成，上下约束与质块M静平衡位置存在的间隙都为.

图1 双侧弹性碰撞悬臂梁系统模型Fig. 1 The cantilever beam system under bilateral elastic impacts

该系统满足如下的动力学方程[11-12]:

2 擦边周期运动

这一节将根据擦边点的定义来给出双擦边周期运动的存在性条件.为了描述擦边周期运动，引入两个分界面，首先定义边界函数

图2 弹性碰撞悬臂梁系统 (2) 的二维相平面Fig. 2 The 2D phase plane of the cantilever beam system under bilateral elastic impacts (2)

基于上面的区域，且考虑k1=k2=k，将系统(2)转化成如下的自治系统：

其中

系统 (5)在区间Vc,Vu,Vd内的通解分别为

3 Poincaré不连续映射及复合映射

本节选取速度为零的 Poincaré 截面来推导弹性约束悬臂梁系统 (2)双擦边周期运动的不连续映射.定义两个零速度的 Poincaré 截面：

这里D1是上方约束截面 Σ1的擦边点附近的区域，D2是下方约束截面 Σ2的擦边点附近的区域.

图3 擦边点附近不连续映射 PPDM1和 PPDM2的示意图Fig. 3 The schematic diagram of the discontinuity mappings PPDM1 and PPDM2 near grazing points

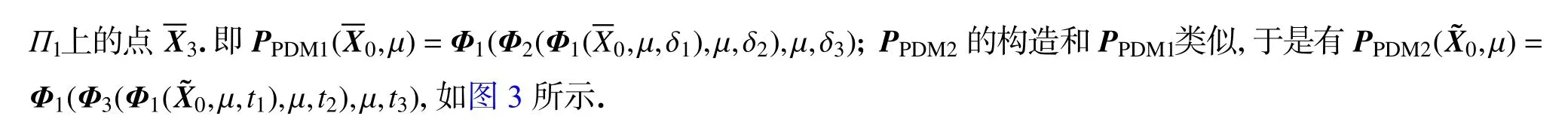
3.1 低阶复合范式映射

式中

将不连续映射 (32)和 (33)代入到式 (38)、(39)、(41)和 (42)中，可得如命题2 所示的低阶复合范式映射.

命题2 双侧弹性约束悬臂梁系统(2)以零速度为截面的低阶的分段复合范式映射为

其中

3.2 高阶复合范式映射

4 数 值 仿 真

取系统的一组参数v=0.1,k1=k2=190,w=0.18，以间隙d为分岔参数，根据命题1 得到擦边分岔点d0=0.033 5.根据低阶映射 (43) 得到擦边点附近分岔图，如图4(a)所示，从图4(a)可以看到擦边附近没有发生明显的分岔.根据高阶映射 (49)得到擦边附近分岔图，如图4(b)所示，从图4(b) 可以看到系统发生了分岔，这说明低阶的范式在一定范围内并不能反映原系统的动力学行为.

图4 系统 (2) 擦边轨道附近的分岔图：(a) 基于低阶映射 (43) 得到的擦边轨道附近的分岔图；(b) 基于高阶映射 (49) 得到的擦边轨道附近的分岔图Fig. 4 The bifurcation diagram of system (2) near the grazing orbit: (a) the bifurcation diagram near the grazing orbit obtained based on low-order mapping(43); (b) the bifurcation diagram near the grazing orbit obtained based on high-order mapping (49)

基于图4(b)通过相图进一步来调查擦边附近的动力学行为，为了方便，这里以符号p-q-s描述系统的碰撞周期运动，其中p表示与上约束面的碰撞次数，q表示与下约束面的碰撞次数，s表示激振力的周期数.从图4(b)可以看到，在擦边分岔点d0的右侧，系统处于稳定的非碰撞单周期运动，如图5 所示.当d=d0时，系统刚好处于擦边周期运动，如图6 所示.当参数d穿越分岔点d0时，系统经过擦边分岔进入稳定的 1-1-1 周期运动，如图7 所示.随着参数的进一步减小，双碰周期一运动发生倍化分岔，系统进入稳定的 2-2-2 周期运动，如图8所示.

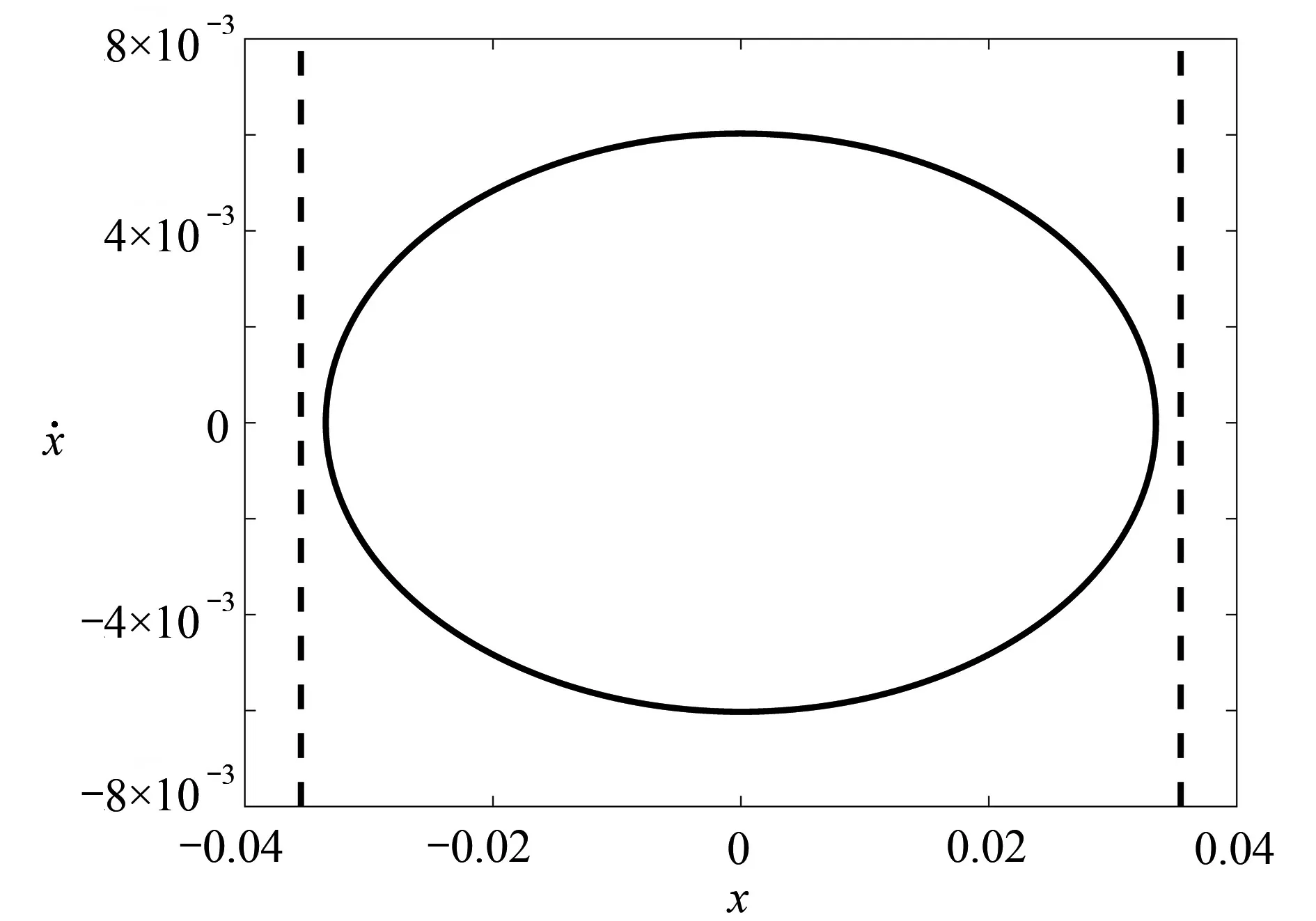
图5 在 d=d0+0.002处的非碰撞单周期运动Fig. 5 The non-impact single periodic motion at d=d0+0.002

图6 在 d=d0处的双擦边周期运动Fig. 6 The double grazing periodic motion at d=d0

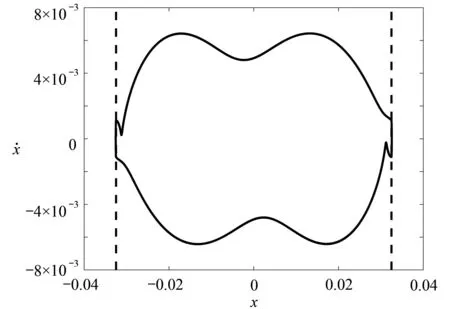
图7 在 d=d0 −0.001处的 1-1-1 碰撞周期运动Fig. 7 The 1-1-1 impact periodic motion at d=d0 −0.001

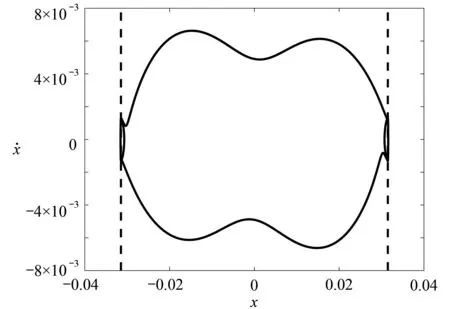
图8 在 d=d0 −0.002处的 2-2-2 碰撞周期运动Fig. 8 The 2-2-2 impact periodic motion at d=d0 −0.002

5 结 论

本文研究了双侧弹性约束的悬臂梁系统的非光滑擦边动力学行为.在建立速度为零的 Poincaré 截面基础上，推导了带参数的高阶范式局部不连续映射，结合不连续映射和光滑映射获得了双擦边运动的高阶复合分段范式映射，一定程度上解决了低阶范式映射在特定参数域内无法反映原系统擦边分岔特性的问题.基于高阶的复合映射揭示了悬臂梁擦边附近的局部动力学行为.

参考文献（ References ） ：

［1］N ORDMARK A B. Non-periodic motion caused by grazing incidence in an impact oscillator[J].Journal of Sound and Vibration, 1991, 145（2）: 279-297.

［2］C HIN W, OTT E, NUSEE H E, et al. Grazing bifurcations in impact oscillators[J].Physical Review E, 1994,50（6）: 4427-4444.

［3］L AMBA H, BUDD C J. Scaling of Lyapunov exponents at nonsmooth bifurcations[J].Physical Review E, 1994,50（1）: 84-90.

［4］F REDRIKSSON M H, NORDMARK A B. Bifurcations caused by grazing incidence in many degrees of freedom impact oscillators[J].Proceedings of the Royal Society of London, Series A: Mathematical, Physical and Engineering Sciences, 1997, 453（1961）: 1261-1276.

［5］L I Q H, WEI L M, AN J Y, et al. Double grazing periodic motions and bifurcations in a vibro-impact system with bilateral stops[J].Abstract and Applied Analysis, 2014, 2014: 642589.

［6］X U J Q, CHEN P, LI Q H. Theoretical analysis of co-dimension-two grazing bifurcations inn-degree-of-freedom impact oscillator with symmetrical constrains[J].Nonlinear Dynamics, 2015, 82: 1641-1657.

［7］W EGER J D, WILLEM V D W, MOLENAAR J. Grazing impact oscillations[J].Physical Review E, 2000,62（2）: 2030.

［8］M OLENAAR J, WEGER J D, WILLEM V D W. Mappings of grazing-impact oscillators[J].Nonlinearity, 2001,14（2）: 301-321.

［9］Z HAO X P. Discontinuity mapping for near-grazing dynamics in vibro-impact oscillators[J].Vibro-Impact Dynamics of Ocean Systems and Related Problems, 2009, 44: 275-285.

［10］Y IN S, WEN G L, XU H D, et al. Higher order zero time discontinuity mapping for analysis of degenerate grazing bifurcations of impacting oscillators[J].Journal of Sound and Vibration, 2018, 437: 209-222.

［11］C ZOLCZYNSKI K, OKOLEWSKI A, BLAZEJCZK-OKOLEWSKA B. Lyapunov exponents in discrete modelling of a cantilever beam impacting on a moving base[J].International Journal of Non-Linear Mechanics, 2017,88: 74-84.

［12］B LAZEJCZK-OKOLEWSKA B, CZOLCZYNSKI K, KAPITANIAK T. Dynamics of a two-degree-of-freedom cantilever beam with impacts[J].Chaos, Solitons and Fractals, 2009, 40（4）: 1991-2006.