基于稀疏低秩张量分解的情绪脑电多域特征提取与分类*

黄金诚高云园佘青山孟 明

(1.杭州电子科技大学圣光机联合学院，浙江 杭州 310018；2.杭州电子科技大学自动化学院，浙江 杭州 310018；3.浙江省脑机协同智能重点实验室，浙江 杭州 310018)

随着信号处理与计算机科学技术的日益发展，基于脑电信号(Electroencephalogram，EEG)的情感计算分析领域也越来越重要。 基于EEG 情绪识别的疾病研究能够辅助医生做出诊断，具有客观、准确的特点，是脑科学中一个重要分支[1－4]。

EEG 是一种以非侵入方式采集的神经心理学信号，在大脑的自发脑电信号中，存在一种由外界事物刺激而产生的诱发电位——事件相关电位(Event-related potential，ERP)。 神经心理学认为，ERP 在一定程度上反映了认知过程中大脑的神经电生理的变化[5]。 利用ERP 潜伏期与波形恒定的特点，结合情绪相关的实验范式，能够对情绪障碍相关精神疾病进行辅助诊断与分析，对于研究抑郁症(Major Depressive Disorder，MDD)、精神分裂(Schizophrenia)等疾病的发病机理与认知偏差有重要价值[6－10]。

近年来，利用机器学习算法对EEG/ERP 进行分析的研究层出不穷，如时域分析、频域分析、时频分析和非线性分析等[11－13]。 这些方法以向量或矩阵的形式存储EEG/ERP 信号，进而提取特征进行分类或分析研究。 由于维度的限制，以向量或矩阵形式存储的EEG/ERP 信号会损失部分固有的空间信息。

张量作为二维矩阵向高维的扩展，能够自然地存储EEG/ERP 的时间、频率和空间信息，从而可以全面、客观地分析EEG/ERP。 本文利用张量能够存储高维数据的优势，将多通道EEG/ERP 以张量的形式表示，更完整地表征了EEG/ERP 信号的多域信息。 但传统张量分解算法对EEG/ERP 张量特征的提取能力有限，其中CP 分解算法(Canonical Polyadic decomposition)多用于脑电分析[14]，提取特征不明显，造成分类性能较差；Tucker 分解算法计算效率低、结果不唯一且易造成维度爆炸[15]。 本文结合ERP 张量低秩、稀疏的特点，提出稀疏正则低秩逼近Tucker 分解算法(Sparse Regulation for Lowrank approach Tucker decomposition，SLraTucker)，对ERP 多域(时域、频域、空间域)特征进行提取，该算法能够在高效分解的同时对特征进行筛选，既保证了特征提取的高效性，又提高了特征的有效性。 在MODMA 数据集上实现了抑郁症(Major Depress Disorder，MDD)患者与正常对照组(Healthy Control，HC)在多种情绪下的分类。 同时，还采用BCI-IV 数据集验证了本文算法的泛化能力。 另外，本文充分发挥SLraTucker 分解算法能够直接提取EEG/ERP空间特征的优势，对MDD 与HC 两组人群的空间域特征进行分析，研究他们在多种情绪刺激下活跃脑区的差异，并提取其动态空间特征，实现对空间层面动态变化的对比，为EEG/ERP 空间特征分析提供了客观的研究方法。

1 材料与方法

本文采用兰州大学抑郁症公开数据集MODMA与BCI 竞赛数据集BCI-IV，分别对SLraTucker 分解算法的有效性及泛化能力进行验证。

1.1 实验范式

兰州大学抑郁症脑电公开数据集MODMA 中的ERP 脑电数据集包括24 名MDD 患者(男13 例，女11 例；年龄16～56 岁)和29 名健康对照者(Healthy Control，HC)(男20 例，女9 例；年龄18～55 岁)共53 例受试者的数据，年龄与性别均无明显差异。 该数据集在经典的点测范式的基础上，增加不同情绪人脸面孔作为刺激线索，使用圆点作为目标探测点，通过外部情绪图片刺激诱发注意力任务下的EEG信号[16]，实验范式如图1(a)所示。

图1 实验范式

BCI-IV-2a 数据集由9个被试者的资料组成，根据不同的刺激分为不同类型的运动想象任务。 首先，简短的声音beep 代表记录开始，两秒钟后，箭头提示出现并在屏幕上停留1.25 s，根据箭头的朝向受试者被要求执行运动想象任务，直到屏幕再次变黑。 每种运动想象任务都有72 次实验，以22个电极记录，实验范式如图1(b)所示。 本文主要选取其中的左手、右手运动想象数据，用于验证SLraTucker分解在不同数据集的泛化能力。

1.2 脑电信号预处理

原始脑电信号中存在大量伪迹信号，需要对其进行预处理以获取较为纯净的ERP 成分[17]，这里使用EEGLAB 工具箱对采集到的EEG 数据进行离线预处理，步骤依次为:滤波、ICA 去除眼电和心电伪迹、基线校正、分段、叠加平均，如图2 所示。

图2 脑电信号的预处理

预处理后的信号包含时域和空间域信息。 本文使用张量对ERP 进行表示，自然地保存了其多域信息，有利于后续全面地提取ERP 信号的多域特征。

1.3 张量基础及基本运算

张量可以看作矩阵向高维空间的拓展，若为张量选取不同的阶数，可以将其拓展为不同的数据类型，其中零阶张量是一个标量，二阶张量是一个矩阵，三阶及以上的张量也就是高维数据空间中的基本数据类型，统称为高阶张量，本文使用高阶张量表征情绪ERP 的多域信息，以保留更全面的原始信息。

1.3.1 符号展示

本文小写字母代表向量，如a∈RI1；大写字母代表矩阵，如A∈RI1×I2；加粗大写字母表示张量A∈RI1×I2×…×IN[18]，运算符号如表1 所示。

表1 基本张量运算符号

1.3.2 ERP 信号的张量表示

针对传统ERP 分析对空间信息保留不全面的问题，本文利用张量模型及其分解算法，表征ERP的多域特征。

经过预处理后的ERP 是以矩阵形式存储的空间(channels)与时间(sample points)的二维数据，本文采用复Morlet 小波变换得到其频域信息，建立以张量形式表示的多域ERP。 本文选用的复Morlet小波变换函数为:

对于二阶(channels×sample points)的单个ERP信号样本X∈Rc×t(其中c代表导联，t代表采样时间点)，通过计算小波函数，可以得到单个样本ERP 三阶张量(channels×sample points×frequency)，以X∈Rc×t×f表示。

本文所使用的情绪脑电数据由129 电极帽采集(其中包含一个参考电极)，截取情绪刺激后的800 ms 作为一个试次(trial)；每10个trial 进行平均，被试的每种情绪刺激下有16个样本；设置频率范围为0.1 到20 Hz，中心频率为0.5 Hz，由此，对于每个样本都能得到一个Xn∈R128×201×40(其中n表示第n个样本)的三维张量，其中128 表示通道数，201表示采样时间点，40 表示频率点。

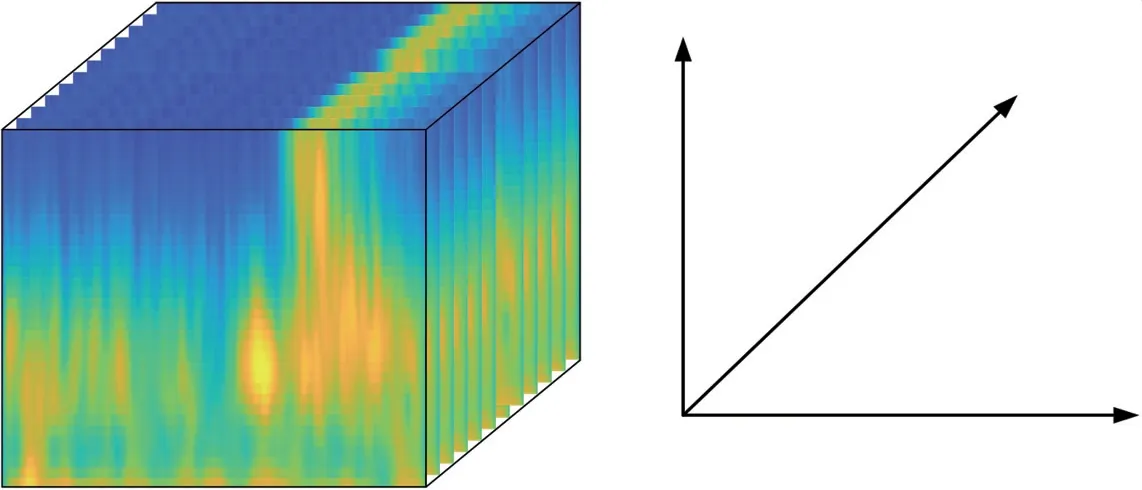
图3 单个样本的ERP 张量

1.3.3 张量的基本运算

给定一个N阶(模)张量Y∈RI1×I2×…×IN，其n模展 开( n-mode Unfolding) 操 作 定 义 为Y(n)∈RIn×∏k≠nIk[18]。 张量Y与矩阵A∈RJ×In沿n模的乘积记 作Y×nA， 得 到 的 结 果 是 一个 张 量Z∈RI1×…In－1×J×In＋1×…×IN，也就是将张量沿n模展开后乘以矩阵A。

对于张量Y∈RI1×I2×…×IN的分解降维，有两种主流的张量分解算法，一种是CP 分解[19，20]，另一种叫做Tucker 分解[21]。 CP 分解是将张量分解为R个秩一张量相加的形式，其中R为张量的秩，且张量的CP 解唯一。 Tucker 分解将原始张量表示为一个核心张量与各个模的因子矩阵相模乘的形式，N阶张量的Tucker 分解由式(2)给出，以三阶张量为例，Tucker 分解如图4 所示。

图4 Tucker 分解

式中:G∈RR1×R2×…×RN为核心张量，A(n)∈RIn×Rn(n＝1，2，…，N)为因子矩阵。 Tucker 分解是矩阵分解的高阶拓展，其每一模的秩都可以根据需要人为设置，设置的模秩不同，张量的Tucker 分解也不同；相较于CP 分解，Tucker 分解可以更方便地增加约束项，如非负约束、稀疏约束等，这使得Tucker 分解在高维数据张量分解中泛化能力更强。 考虑到ERP 张量稀疏、低秩的特点，本文选取Tucker 分解提取多域ERP 特征。

由于Tucker 分解的不唯一性，若将每个样本张量都单独进行张量分解，取其核心张量作为多域特征，可能存在不同样本的特征处于不同的高维空间的情况，从而使得特征在后续分析、分类中无意义。为此本文在原有单样本三阶张量的基础上增加一维，如图5 所示，将所有的样本张量在这一维度上排列，得到一个X∈R128×201×40×848的四维张量。 在后续的张量分解中，同时在X的前三维度进行分解，这样所有的特征张量共享同一套因子矩阵，也就是以相同的张量空间基矩阵进行估计。

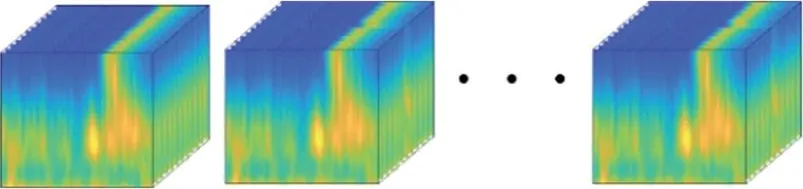
图5 所有被试的ERP 张量

1.4 稀疏正则的低秩逼近Tucker 分解算法

按照上述数据结构生成的ERP 张量规模十分庞大(如本实验所生成的张量在HDF5 编码下以双精度存储达1G)，使用传统张量分解优化算法如交替最小二乘法(hierarchical alternating least squares)效率较低[22，23]。 由于张量分解本质上为无监督学习算法，通过对张量分解添加约束往往可以起到减少计算量、提高收敛速度的作用[24，25]。 另外，ERP样本中存在大量的冗余信息，如背景噪声、冗余通道等，使得ERP 样本张量表现出低秩、稀疏的特点。传统脑电张量分解算法[14]未能考虑脑电在张量域所表现出的特性，直接将在图像领域较为成熟的张量分解算法应用于脑电上，效率较低且对于脑电张量应用的泛化能力较差。 本文利用Tucker 分解算法的优势，结合ERP 张量的低秩、稀疏的特点，提出稀疏正则的低秩逼近顺序张量分解算法，即SLraTucker 分解算法，实现对ERP 成分的多域特征提取。

传统Tucker 分解算法在运算时，每一次迭代都需要做一次张量的n模展开(mode-n unfold)，从而造成计算效率较低。 LraTucker 分解(Low-rank approach Tucker decomposition)利用张量的n模展开将传统Tucker 分解(2)进行重写:

得到矩阵Y的低秩逼近表示后，通过固定和，将其带入式(4)得到新的目标函数

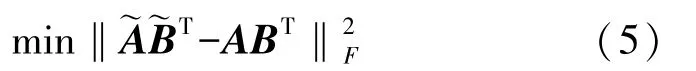
LraTucker 分解算法结合数据张量的低秩性，表现出十分高的效率，但与传统Tucker 分解一样，在EEG 中应用易造成维度爆炸，有一定局限性。 为了提高在EEG/ERP 张量分解中的泛化能力，并使得提取的特征更加明显，本文在LraTucker 分解中添加稀疏正则项λS(A)

式中:S(·)为稀疏表示，如L0 范数｜A｜0和L1 范数｜A｜1在实际应用中都存在一些问题(求解L0 范数是一个NP 难问题，L1 范数在0 点不可导)，这里我们使用下式作为稀疏表示函数:

利用梯度下降法对式(6)进行更新，分别对A和B进行求导，得到:

选取α为与最终得到SlraTucker 分解的更新公式如下:

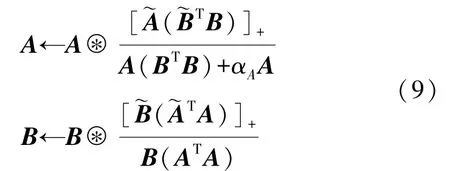
由于只需进行一次n模展开，使用如上的更新规则求解Tucker 分解较传统方法可以少进行倍的n-mode 展开，且加入的稀疏正则项使得该算法在EEG/ERP 张量中具有更强的泛化能力。

1.5 特征提取流程

本文SLraTucker 分解算法对情绪ERP 张量进行特征提取流程如图6 所示，得到的核心张量用于分类，表征空间特征的因子矩阵以脑地形图的形式呈现，以便分析空间特征。 具体特征提取过程如下:

图6 特征提取流程示意图

(1)采用50 Hz 陷波滤波器与0.3 Hz～30 Hz 带通滤波器滤波；重参考。

(2)分段平均:以刺激的出现作为刺激开始的标志，截取刺激后的800 ms 作为一个trial，采样频率为250 Hz。 对于每个个体，将同一刺激下的10个样本进行叠加平均，以提取较为纯净ERP 成分。

(3)生成样本张量:①将叠加后的样本按照通道依次通过复Morlet 小波变换映射到时频域，频率范围取0.5 Hz～20 Hz，步长为0.5 Hz，则对于每个通道都得到一个201 × 40 的二维矩阵(time ×frequency)；②将变换后的数据按通道的顺序在张量的第一维度排列，得到一个维度为128×201×40 的三维张量(channels×time×frequency)，自然地包含了每个ERP 样本的空间、时间、频率信息；③将得到的三维张量在第四个维度排列，每个被试的每种情绪刺激下有16个样本，生成一个维度为128×201×40×(16×53)的四维张量(channels×time×frequency×(subject×trials))，此四维张量即为样本张量。

(4)使用SLraTucker 分解对样本张量的前三维度同时进行张量分解，得到的核心张量为包含了原始信号中多域特征的特征张量，因子矩阵可以看作样本所共有的多域信息。

按照上述步骤对ERP 数据张量进行特征提取，得到的核心张量是每个样本所特有的特征在核心张量第四维度的排列，因子矩阵为所有样本共享的共同特征。 如此得到的脑电多域特征包含了空间、时间和频率特征，且经过张量分解能够直接得到空间特征，相比传统方法更加直接。

2 结果展示

2.1 分类结果

利用本文的算法提取情绪ERP 的多域特征，将每个被试所特有的特征——核心张量经过向量化后输入到SVM 中，分别在愉快、悲伤和恐惧情绪刺激下获得91.5%、90.6%和84.3%的识别率，较传统Tucker 分解平均提升13.4%，较LraTucker 分解平均提升4.7%。 为直观展现张量分解作为特征提取方法的优势，本文将其与通过改进内核目标对齐(modified kernel-target alignment，mKTA)[26]进行空间特征筛选的方法进行比较。

文献[27]采用mKTA 作为其空间特征选择算法，选取的通道数从1 增加到58，通过支持向量机(SVM)得到平均分类结果，在选取19个通道时识别准确率达到最高，即80.0%。 本文提出的SLraTucker 算法能够直接在特征提取的过程中进行空间特征筛选，加入的稀疏正则也一定程度上进行了特征筛选，保留了更加明显的特征，从而提高了模型的分类性能。 如表2 所示，SlraTucker-SVM 分类方法实现的患者平均识别率为88.9%，相较于mKTA方法，分类效果提升了8%以上。

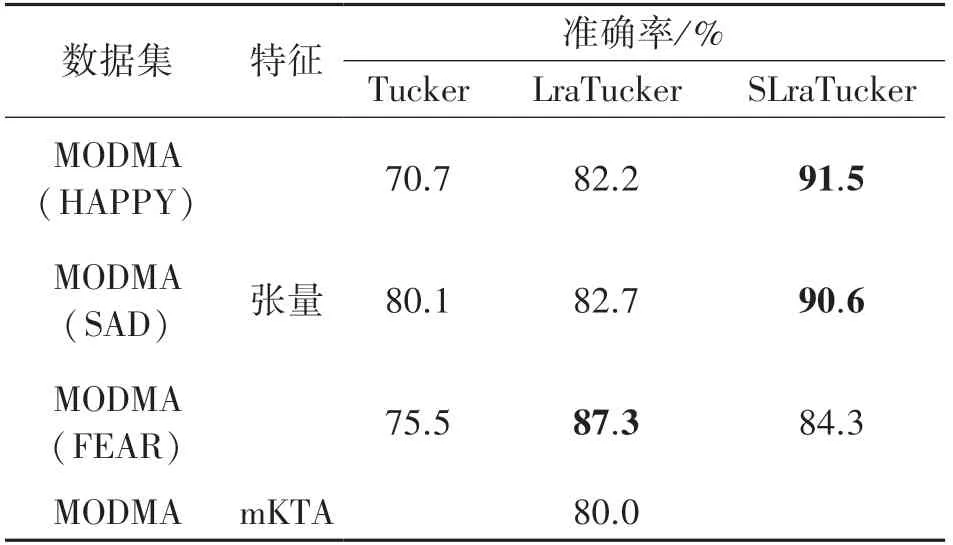
表2 MODMA 数据集实验结果

为验证本算法在EEG 领域的泛化能力，选取BCI-IV 数据集，进行与MODMA 数据集相同的滤波预处理，并生成张量，分别应用传统Tucker 分解、LraTucker 分解和本文提出的SLraTucker 分解算法对原数据进行特征提取。 在内存为8GB，CPU 为i5-8265u 的平台上，对BCI-IV-2a 数据集的9个被试张量进行分解，传统Tucker 分解算法平均运行时间为1 000.726 2 s，达到平均76.72%的原始数据张量相似度；LraTucker 分解平均运行59.759 4 s，达到平均78.72%的相似度；而SLraTucker 分解算法平均运行时间为57.638 0 s，较传统Tucker 分解计算效率提升约16 倍，达到78.66%的相似度。 提取出的核心张量对于原张量的还原度如表3(fit mean)所示，选取10 折交叉验证SVM 对其分类，准确率如表3 与图7 所示.

表3 BCI 数据集实验结果

图7 BCI 数据集准确率

2.2 静态空间特征提取结果

采用SLraTucker 分解算法对MDD 与HC 两组人群不同情绪刺激后800 ms 内的多域特征进行提取，该算法是在前三维度上对全部样本张量进行估计的过程，得到的因子矩阵为其所有样本所共有的特征。为此，本文通过分别生成MDD 与HC 各自的样本张量，利用SLraTucker 算法对两个样本张量分别分解，得到MDD 患者样本张量与HC 对照组样本张量的Tucker 分解。 为观察两类人群在不同情绪刺激下活跃脑区的异同，将表征空间特征的mode-1 因子矩阵以脑地形图的形式呈现，脑区位置如图8 所示。

图8 脑地形图脑区标注

图9 中展示了两类人群在悲伤情绪刺激下的脑地形图，从HC 对照组可以看出，大脑主要在额叶和顶叶比较活跃，而MDD 患者顶叶的活跃度较低，枕叶活跃度略高于HC 对照组，额叶右侧活跃度较HC对照组更大，但活跃程度度偏低。

图9 悲伤刺激下脑地形图对比

从图10 中可以看出，HC 对照组在“愉快”情绪刺激下表现为额叶活跃，MDD 患者虽然活跃区域与HC 对照组类似，但枕叶活跃程度较HC 对照组偏低，且顶叶存在活跃。

图10 愉快刺激下脑地形图对比

对于“恐惧”刺激，如图11 所示，HC 人群活跃脑区在左前额叶、右前额叶有较高活跃度，枕叶也存在一定活跃度，与HC 对照组不同的是，MDD 患者的高活跃区主要在右前额叶和顶叶，枕叶则表现为低活跃状态。

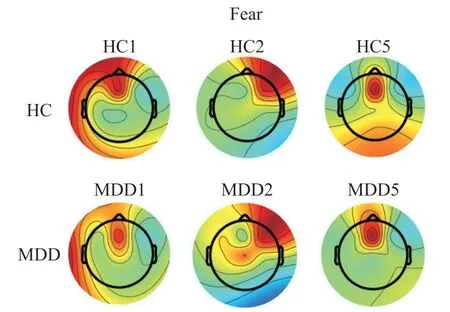
图11 恐惧刺激下脑地形图对比

2.3 动态空间特征提取结果

为了动态地分析ERP 的变化情况，我们选取长度为200 ms，重叠率为50%的滑动时间窗。 结合HC 对照组与MDD 患者800 ms 脑地形图的差异从128个通道中选择了包括额叶、中央区、顶叶、枕叶的20个电极，如表4 所示，针对每类人群分别生成数据张量，利用SLraTucker 算法对每个时间段内的样本张量分别进行分解，把核心张量中对应空间特征的mode-1 因子矩阵以脑地形图的形式呈现。

表4 通道选择

根据图12，在“悲伤”情绪刺激下，MDD 额叶左侧的活跃从前期出现保持至后期，而HC 的额叶左侧活跃度则从前期出现，并于中期开始下降。 在0～800 ms 时间段内，MDD 患者活跃脑区存在不对称的现象，而HC 则较为对称。

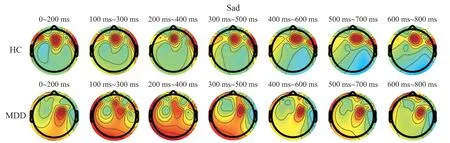
图12 悲伤刺激下动态脑地形图对比

根据图13，在“愉快”情绪刺激下，MDD 活跃脑区变化并不明显，主要集中于顶叶右侧、中央区右侧和右前额叶，有小幅能量波动，而HC 对照组的额叶左侧、中部、右侧和枕叶等都有能量上升以及活跃区域增大。

图13 愉快刺激下动态脑地形图对比

通过图14 我们发现，在“恐惧”情绪下MDD 患者活跃脑区向左前额叶移动，中期左前额叶出现活跃并持续至后期，HC 对照组的活跃脑区则向两侧额叶移动，从中期开始，左右两侧额叶的活跃度都有所上升。

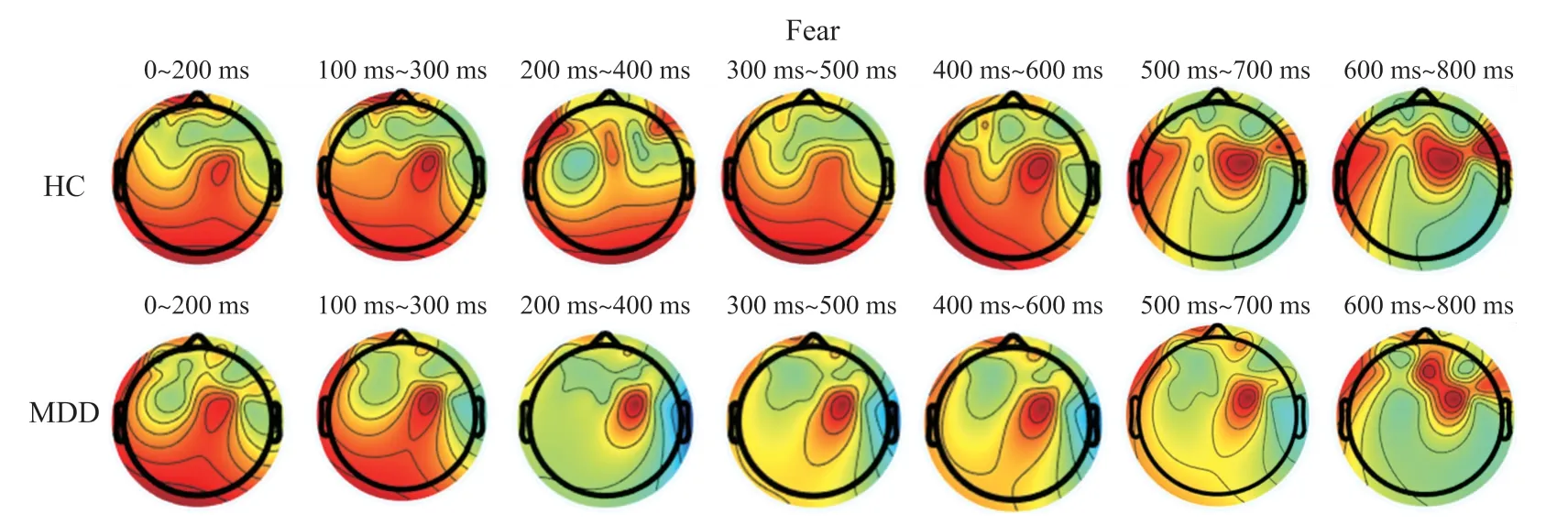
图14 恐惧刺激下动态脑地形图对比

3 讨论

本文以张量的形式存储、表示情绪ERP，利用ERP 张量稀疏、低秩的特点，提出SLraTucker 分解算法对情绪ERP 张量进行多域特征提取。

SLraTucker 分解在计算过程中只需要进行一次n模展开，较传统Tucker 分解少进行次n-mode 展开，同时加入稀疏正则化，使得SLraTucker算法在ERP 分析中表现出更强的泛化能力。

由于稀疏约束对于权重较低的特征有置零的作用，相比LraTucker 分解，SLraTucker 分解对于张量的还原能力存在小幅下降，但得益于稀疏约束特征选择剔除冗余特征，SLraTucker 分解算法在分类准确率上较LraTucker 分解平均提高4.7%，较传统Tucker 分解算法提升了17.5%。

按照二维情绪模型，从效价和唤醒两个维度分析[27]，“恐惧”为负性高唤醒情绪，“悲伤”为负性低唤醒情绪，“愉快”为正性低唤醒情绪。 通过对刺激后800 ms 时间段的脑地形图进行分析，在效价维度上，在效价为负的“悲伤”、“恐惧”情绪刺激下，MDD患者的额叶表现出低于HC 对照组的活跃度；在正性情绪“愉快”刺激下，MDD 患者额叶活跃度低于HC 对照组，而中央区和顶叶活跃度则要高于HC 对照组。 在唤醒维度上，“恐惧”为高唤醒情绪刺激，MDD 患者的顶叶、中央区三部分活跃度高于HC 对照组。 MDD 患者额叶活跃度低于HC 对照组，且MDD 患者更易被负性情绪激活。 额叶是情绪调控的高级中枢，也是认知、感觉和运动等多级协调体系的重要中枢。 姚树桥等[28]认为抑郁症患者对于正负性刺激的不同ERP 效应，可能涉及前额叶左、右半球不同区域的功能整合；Kayser 等[29]认为抑郁症患者的脑地形图表现出大脑不对称性，造成评价过程出现异常，这也与我们通过分析刺激后的800 ms的脑地形图得出的结论一致。 此外，由于情绪的产生是一个动态的过程，本文通过增添滑动时间窗口的方式，探究了在不同情绪诱发下两组人群活跃脑区的动态变化。

根据图12～图14，可以发现MDD 患者对效价的敏感度高于HC 对照组，而对于唤醒度则刚好相反。对于负性情绪，MDD 患者对唤醒度更强的“恐惧”情绪刺激不敏感，其额叶左侧活跃出现时间更晚且持续时间较短，反观HC 对照组则较为敏感，额叶左侧早期就出现活跃并持续到后期；MDD 患者对于效价更低的“悲伤”情绪刺激更加敏感，额叶左侧活跃从早期出现，并在中期、后期持续保持活跃状态，活跃脑区不对称的现象明显，HC 对照组早期产生的左前额叶活跃在中期即开始下降。 对于正性情绪，MDD 患者活跃脑区变化十分微小，在左前额叶、右中央区和右顶叶有小幅度能量上升，顶叶表现出激活困难的现象；反观HC 对照组的额叶活跃度变化幅度较大。 综上所述，在负性情绪刺激下，MDD 患者的额叶脑区活跃持续时间更长，且存在不对称现象。 对于正性情绪MDD 患者的脑区更难被激活。

结果表明，MDD 患者对于效价低的情绪更加敏感，脑区活跃程度大、持续时间更长，而对于正性情绪则存在选择性抑制，表现出难以被激活的现象。Leuchter 等人[3]的研究结果显示，抑郁症患者在前额叶区、顶叶区、颞叶区相干性连接与正常人存在差异，Kayser 等[29]认为抑郁症患者由于右顶叶情绪刺激感知区域的选择性抑制，会造成评价过程出现异常，这与我们动态脑地形图得出的结论一致。 另外，由本文算法提取的动态脑地形图显示，MDD 患者对于效价的敏感度高于HC 对照组，而对于唤醒度的敏感度则低于HC 对照组，这也进一步验证了800 ms 静态分析的结果。

4 结论

张量是分析、研究EEG/ERP 等高维数据的强有力工具，结果表明，本文提出的SLraTucker 分解算法能够高效地提取情绪ERP 张量中的多域特征。在MODMA 数据集上验证了其有效性，并在BCI-IV-2a 数据集上验证了其具有较强的泛化能力。 由SLraTucker 分解提取出的空间特征以脑地形图呈现，比较和讨论了在不同的认知情绪处理过程中，抑郁症患者与正常对照人群活跃脑区的区别与联系，通过动态分析发现MDD 患者对于效价的敏感度高于HC 对照组，对于唤醒度的敏感度则刚好相反。 本文提出的SLraTucker 分解算法为基于情绪脑电的分析提供了新的方法和思路。