Rotational Hypersurfaces with Constant Gauss-Kronecker Curvature

Yuhang LIU Yunchu DAI

1Beijing International Center for Mathematical Research,Peking University,Beijing 100871,China.E-mail: liuyuhang@bicmr.pku.edu.cn

2Department of Mathematics,Building 380,Stanford University,California 94305,USA.E-mail: daviddai20030815@gmail.com

Abstract The authors study rotational hypersurfaces with constant Gauss-Kronecker curvature in Rn.They solve the ODE associated with the generating curve of such hypersurface using integral expressions and obtain several geometric properties of such hypersurfaces.In particular,they discover a class of non-compact rotational hypersurfaces with constant and negative Gauss-Kronecker curvature and finite volume,which can be seen as the higher-dimensional generalization of the pseudo-sphere.

Keywords Differential geometry,Gauss-Kronecker curvature,Ordinary differential equation

1 Introduction

In the field of differential geometry,curvature is the quantity used to measure the extent to which a geometrical object bends.In the study of submanifold geometry,the principal curvatures describe how the submanifold bends in each principal directions.The mean curvature is the mean value of all principal curvatures,while the Gauss-Kronecker curvature is the product of principal curvatures.For the rest of the paper we will call it Gauss curvature for short.Various notions of curvatures have many applications in science and industry.The problems on various restrictions on those curvatures have a long history.In particular we focus on the study of submanifolds with constant or prescribed curvature,and most of the time we only consider hypersurfaces,namely,codimension one submanifolds.The constant mean curvature(CMC for short)submanifolds can be seen as generalizations of minimal submanifolds,which are characterized as having zero mean curvature.CMC hypersurfaces enjoy good variational and geometric properties.For a detailed survey on CMC hypersurfaces in Rn,we refer the readers to [1].We mention a few results here,which motivate our work.In terms of rotational CMC surfaces in R3,Delaunay proposed a beautiful classification theorem which indicates that the generating curves of these surfaces are formed geometrically by rolling a conic along a straight line without slippage (see [5]).In the 1980s,Hsiang and Yu generalized Delaunay’s theorem to rotational hypersurfaces in Rn(see [6–7]).Recently Buenoa,Galvezb and Mirac studied the more general question about rotational hypersurfaces with prescribed mean curvature and obtained Delaunay-type classification theorems (see [2]).

On the other hand,higher order symmetric functions of the principal curvatures are also interesting.Ther-th symmetric function of the principal curvatures is called “r-mean curvature”,which covers the notions of mean curvature and Gauss curvature whenris equal to 1 and the dimension of the hypersurface,respectively.In 1987,Ros proved that a closed hypersurface embedded into the Euclidean space with constantr-mean curvature is a round sphere (see [9,11]).There are also results on hypersurfaces with constant or prescribed Gauss curvature in other ambient spaces.See e.g.[12–13].

However,we notice that few examples on constant Gauss curvature hypersurfaces in Rnhave been constructed and studied in the literature,other than the round spheres and flat planes.According to Ros’theorem,either such hypersurfaces are non-compact or they have non-empty boundary,if they are not the round spheres.They could still carry interesting geometric and analytic properties.The condition of having constant Gauss curvature is characterized by a Monge-Ampere type equation,and special explicit solutions to such equations can shed light on the study of general solutions.Looking for constant Gauss curvature hypersurfaces with enough symmetry could be an initial step of the study of general hypersurfaces with constant Gauss curvature.Just as Delaunay-type hypersurfaces have been built blocks of general CMC hypersurfaces in Rn,hypersurfaces with special symmetry conditions can be testgrounds for general hypersurfaces with constant or prescribed Gauss curvature.

In this paper,we focus on rotational hypersurfacesMwith constant Gauss curvatureKin Rn.Letγ(t)=(ϕ(t),ψ(t)) be a parametrization of the generating curve ofM.We derive the following ODE forϕ(t):

We solve this equation and obtain the following result.

Theorem 1.1Let M⊂Rnbe a rotational hypersurface with constant Gauss curvature K such that its generating curve γ is a graph over the axis of rotation.Let γ(t)=(ϕ(t),ψ(t))be a parametrization of the generating curve,where ϕ(t)is the radius of the meridian(n−2)-sphere,ψ(t)is the height function and t is the arclength parameter.Then:

(1)When K=0,M is a circular cone or a circular cylinder.

(2)When K≠0,the expression of the inverse function of ϕ is locally given by

where the sign of the integrand agrees with the sign of ϕ′,t0is the initial time,CKis a realconstant.Moreover,ψ is given by

(3)When K <0and CK=−1,the corresponding hypersurface is a complete Riemannian manifold(with boundary)diffeomorphic to Sn−2×[0,+∞)and has finite volume.It can be seen as a higher-dimensional generalization of the pseudosphere in dimension two.

More precise statements are made in Theorems 3.2–3.4.The pictures of the generating curves are displayed in Figures 1–2.The hypersurface in (3) in Theorem 1.1 is the only noncompact example.We also note that whenn=3,classifying constant curvature surfaces of revolution is a classical problem and was completely solved long ago.See e.g.[3,Chapter 3–3,Exercise 7].Using the explicit formula for the solutions,we also study how the shape of the generating curve changes as the Gauss curvatureKvaries,see Subsection 3.3.

We remark that rotational hypersurfaces in space forms have been systematically studied,e.g.in [4,8,10].In particular,Palmas concluded that the only complete rotational hypersurfaces (without boundary) with constant Gauss curvature in the Euclidean spaces are hyperplanes,cylinders and round spheres (see [10]).We follow the orbit geometry approach in their papers,and we allow the hypersurfaces to have boundary or to be singular.In particular,we discover a class of non-compact rotational hypersurfaces with constant and negative Gauss curvature which have finite volume.To the best of our knowledge,we have not seen such examples discussed in the literature.

2 Rotational Hypersurfaces and Its Curvatures

We set up notations and state the formulae for principal curvatures and Gauss curvature of a rotational hypersurface in Rn.Letx1,x2,···,xndenote the standard coordinates of Rnand we assume thatxnis the axis of rotation.Letf:R→(0,+∞) be a smooth function.

Definition 2.1A hypersurface M is called a rotational hypersurface if it is produced by rotating the generating curve x1=f(xn)in the x1xn-plane around the xn-axis.It is characterized by the following equation

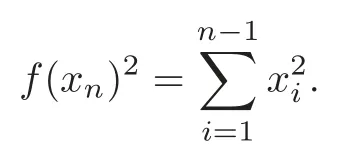
Note thatf(xn) is the radius of the horizontal subsphere at heightxn.Throughout this paper,Mwill always denote a rotational hypersurface in Rnunless otherwise stated.

We choose an appropriate parametrization of the generating curve to facilitate the calculation.Letϕ(t) denote the radius of then−2 dimensional hypersphere andψ(t) denote the corresponding height.We choose the parametertto be the arclength parameter,that is,ϕ′2+ψ′2=1.Under the above parametrization,the generating curvex1=f(xn) is parametrized as (x1,xn)=(ϕ(t),ψ(t)).Note thatϕ(t)≥0 since it is the radius,and we requireψ′(t)≥0 so that the generating curve is a graph over thexn-axis.

We use the hypersphere coordinate (ϕ,θ1,···,θn−2) to parametrize the rotational hypersurface.The position vector field of rotational hypersurfaceMcan be written as

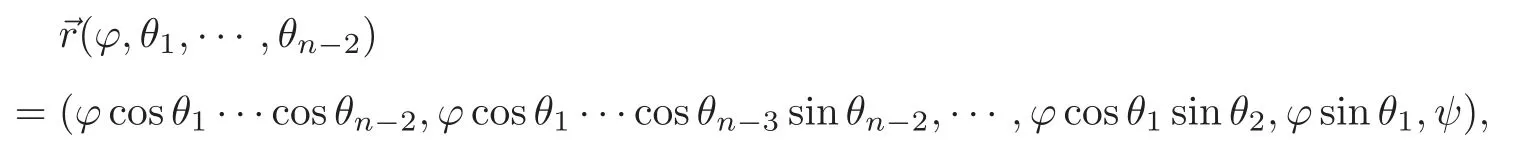
Under the above parametrization,the principal curvatures and the Gauss curvature ofMare given in the following theorems,respectively.

Theorem 2.1The principal curvatures k1,···,kn−1of M are given below:

Theorem 2.2The Gauss curvature K of M is given below:

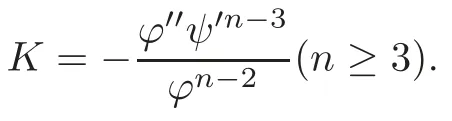
Detailed calculations can be found in [2,Section 2].

3 Analysis of Rotational Hypersurface with Constant Gauss Curvature

We require the Gauss curvature of rotational hypersurfaceMto be a constantK.Then the equation in Theorem 2.2 is transformed into an ODE as below:

This equation will be the main equation that we study in this paper.Here we require thatψ′≥0,so that the generating curve is a graph over thexn-axis.In this section,we will solve this equation by separation of variables.

3.1 Solutions to the ODE

WhenK=0,we get

Obviously,we must haveϕ′′≡0 orϕ′≡±1. Both yields

Thus we have the following theorem.

Theorem 3.1A rotational hypersurface with constant Gauss curvature K=0is one of the following:

(1)A right straight cylinder inRn.

(2)A right circular cone inRn.

ProofFrom (3.2),we know that the generating curve is a straight line in the case whereK=0.Consider the equation

whenc1=0,ϕis a constant in which caseMis a right straight cylinder.Otherwise,whenc1≠0,Mis a right circular cone.

Remark 3.1In fact,the Gauss curvature of any cylinder or cone is 0.

In the rest of the paper,we will therefore discuss the case whereK≠0.We rewrite (3.1)in the following form:

Multiply both sides byϕ′and integrate both sides,we have

whereCKis a constant to be chosen.

Sinceϕis the radius parameter,we only consider the case whereϕ≥0.First,we notice that the solutionϕis bounded.

Lemma 3.1ϕ is a bounded function such that

(1)for K >0,where CK>−1;

(2)for K <0,where CK<0.

ProofFrom (3.4),we get

ForK >0,we further yield

Since we only consider the case whereϕ≥0,we have

Here,we must haveCK>−1 to make sure that

Similarly,we can deduce the inequality forK <0,

Here,we must haveCK<0 to make sure that

Now we solve the ODE whenK >0 andK <0,respectively.

Theorem 3.2Suppose K >0.Let ϕ be a solution to the ODE(3.3),then:

(1)The inverse function of ϕ is given by

where t0is a fixed initial time.

(2)The solution ϕ can be defined on the interval I=[C′,C′+T],where C′is a real number,

and ϕ(C′)=ϕ(C′+T)=

(3)The sign of the integrand is+for t∈and−fororthe other way around if the orientation of the generating curve is reversed.

ProofFrom (3.4),we get

and

Here,the sign of dtagrees with the sign ofϕ′.

Then integrate both sides of the above equation,and we get

We also note that the solutionϕis invariant under time translation and reversion,and thus the value oft0does not affect the shape of the generating curve.

Now,we should consider the interval of definition for this solution.From Lemma 3.1,we know that the integrand in (3.6) is bounded from both above and below.We try to integrate from the lower bound to the upper bound and show that the integral converges,that is,we claim

To prove the claim,we only need to check the singularity whenϕreachesLetand the Taylor expansion of the integrand asA−ϕ→0 is given below:

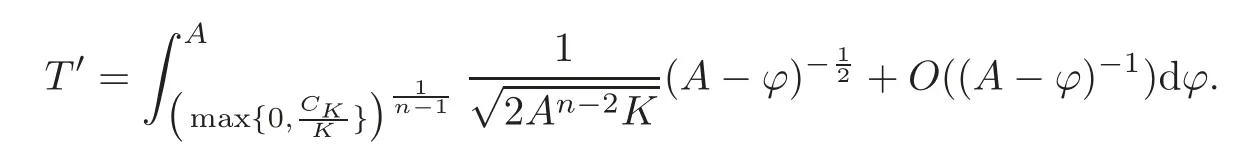
Since the order of the main term of the integrand in terms of (ϕ−A) is greater than−1,the claim is clearly true.

Thus the solutionϕ(t) can be defined on a time interval of lengthT′,say [t0,t0+T′].Without loss of generality,we may assume thatϕ(t) is increasing on [t0,t0+T′],that is,the sign of the integrand in (3.6) is positive.In this wayϕ(t) reaches its minimum att=t0and its maximum att=t0+T′.

Now we extend the solutionϕ(t) to the interval [t0,t0+2T′]by reflection.Namely,we defineϕ(t)=ϕ(2t0+2T′−t).Since(3.3)is invariant under time translation and reversion,this extension ofϕis a solution to the equation.By checking that the (2n+1)storder derivatives ofϕatt=t0+T′equal zero,we know that the left derivatives and right derivatives ofϕagree att=t0+T′.Therefore,we know thatϕ(t) is smooth fort∈[t0,t0+2T′].

Thus we obtain a solutionϕon [t0,t0+T]satisfying all the desired properties,where

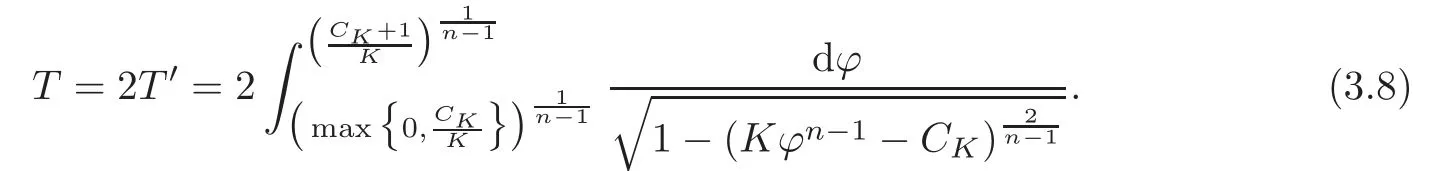
Remark 3.2WhenCK=0,the solution becomesϕ(t)=In this case,Mis the round sphere of constant Gauss curvatureK.

Recall thatϕ′2+ψ′2=1,by (3.4) we have

Thus using the parametrization (ϕ(t),ψ(t)) of the generating curve,we draw the pictures of the generating curves using Mathematica.Figures 1(a)and 1(b) show the generating curves forK=1,CK=−0.5 andK=1,CK=2,respectively.

Similarly,we can describe the solution forK <0 as follows.

Theorem 3.3Suppose K <0.Let ϕ be a solution to the ODE(3.3),then:

(1)The inverse function of ϕ is given by

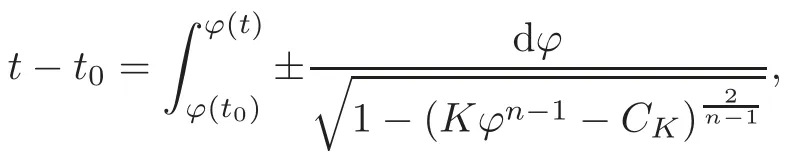
Figure 1

where t0is a fixed initial time.

(2)When CK≠−1,ϕ can be defined on[C′,C′+T]∪[D′−T,D′],where C′,D′are tworeal numbers such that ϕ(C′)=ϕ(D′)=where

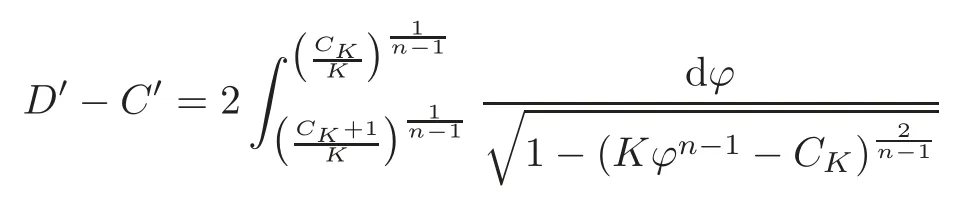
and

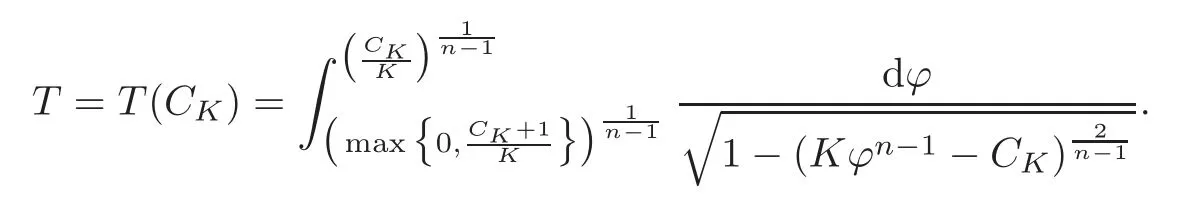
In this case,the sign of the integrand is−in the interval[C′,C′+T]and+in the interval[D′−T,D′].Or the other way around if the orientation of the generating curve is reversed.

(3)When CK=−1,we fix the sign of the integrand to be positive.Under this convention,the interval of definition of the solution to(3.3)extends to−∞.In particular,the corresponding hypersurface is non-compact complete and unbounded in the xn-direction.

ProofSimilar to Theorem 3.2,we can derive the inverse function ofϕas follows

WhenCK≠−1,we also claim

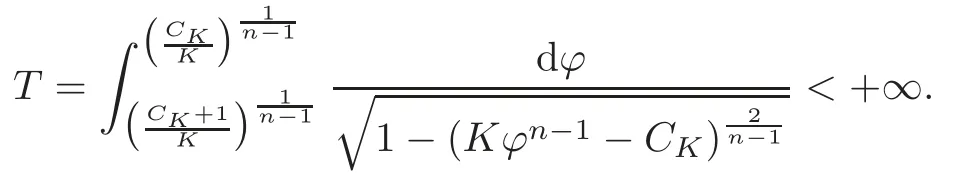
To prove the claim,we similarly letThen,the Taylor expansion of the integrand asϕ−A→0 is given by

Clearly,the integral converges since the order of the integrand’s main term is greater than−1.

Thus by the same reflection argument as in the proof of Theorem 3.2,we can show thatϕcan be extended to a smooth solution defined on[t0,t0+2T],whereTis the above integral andt0can be any real number.Moreover,we can prescribe its monotonicity by fixing the orientation of the generating curve.However,in this wayϕcan be negative somewhere.After deleting the interval on whichϕis negative,we obtain the desired form of the domain of definition ofϕ.

Finally,whenCK=−1,we need to prove that the integral in (3.3) diverges,namely

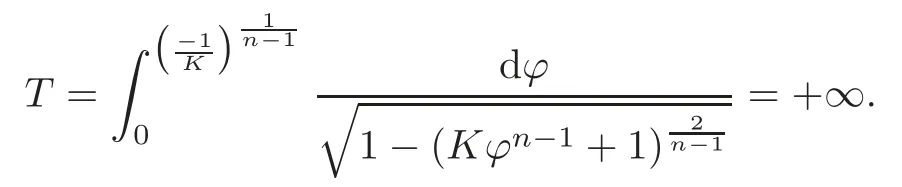
Thus the interval of definition ofϕcan extend to−∞.

We consider the behavior of the integrand when

Letx=Kϕn−1,wherex<0.Then let

After expandingf(x) atx=0 with Taylor Series,we get

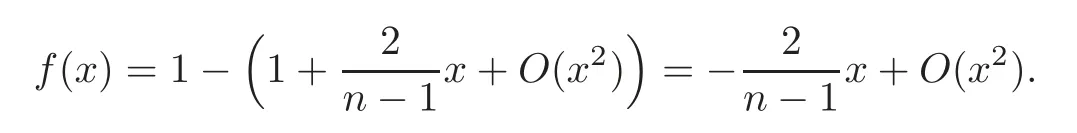
Then we can rewrite the integrand as

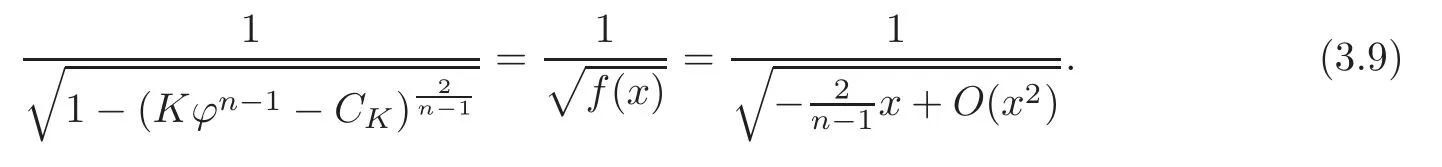
Clearly,we know that the order of the integrand in terms ofϕis equal to the order of its main term,namelybecausex=Kϕn−1.Whenn >3,we know that the order of the integrand is less than−1,which implies that the integral diverges whenϕ→0.

Now we see that astgoes to−∞,ϕ→0 andϕ′=→0 (we have fixed the sign ofϕ′to be positive).Thusψ′=andψ→−∞(because we lettdecrease to−∞).Recall thatψis the height function.This shows that the generating curve is an unbounded curve asymptotic to the axis of rotation.Thus the rotational hypersurface corresponding toCK=−1 is complete as a metric space.

Remark 3.3The hypersurface corresponding toCK=−1 in the above theorem can be seen as a higher-dimensional generalization of the pseudo-sphere in dimension two.Our results do not contradict Ros’ theorem in [11]since the hypersurfaces in our theorem have non-empty boundary.We also note that we can find a non-compact solution only whenK <0 andCK=−1.In all other cases,the corresponding hypersurfaces are compact with boundary or compact with conical singularities at the axis of rotation.

Using Mathematica,we draw the generating curves forK <0.Figure 2(a) depicts the generating curve of the non-compact hypersurface corresponding toCK=−1,while Figures 2(b) and 2(c) show the generating curves forK=−1,CK=−0.5 andK=−1,CK=−2,respectively.

Using the integral expression of the solutionϕ,we can calculate its Taylor expansions at critical points in order to extract more information about the local behavior ofϕ.

Lemma 3.2The series expansion of ϕ(t)near ϕ(t0)=ϕmaxwhen K >0is given by

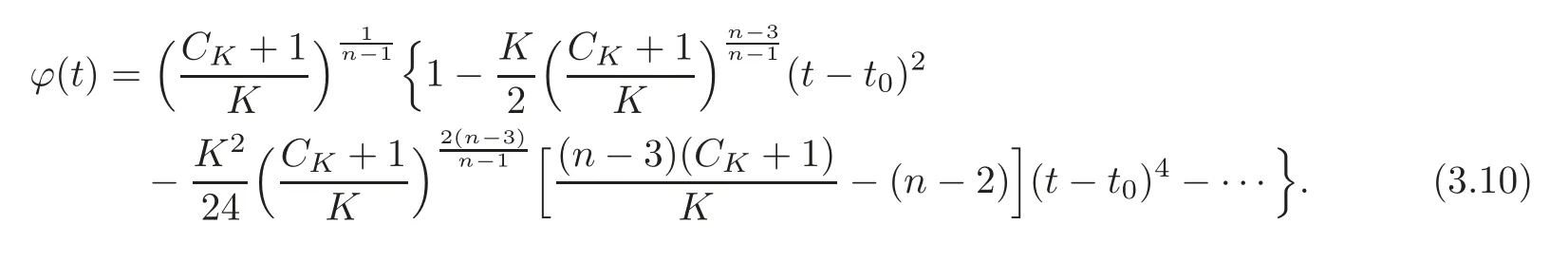
ProofBy (3.5),we know that the first order derivative ofϕnear its maximum is zero.Then,we can further compute its second order derivative as

Similarly,we can compute its 4thorder derivative,and so on.Notice that the sign of these derivatives are negative nearϕmax,we can get the series shown above by using Taylor expansion.

Lemma 3.3The series expansion of ϕ(t)near ϕ(t0)=ϕminwhen K <0and CK<−1isgiven by

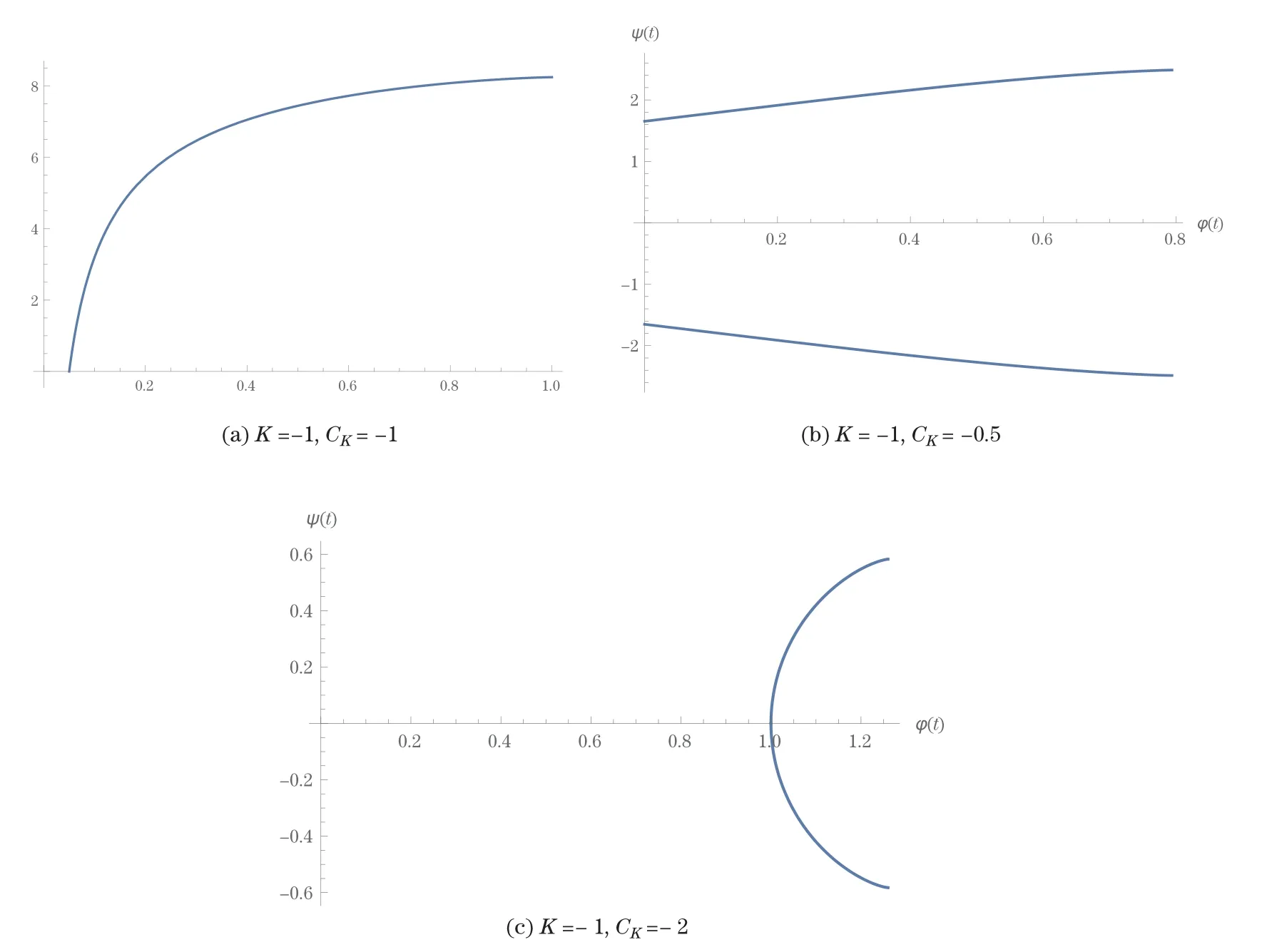
Figure 2

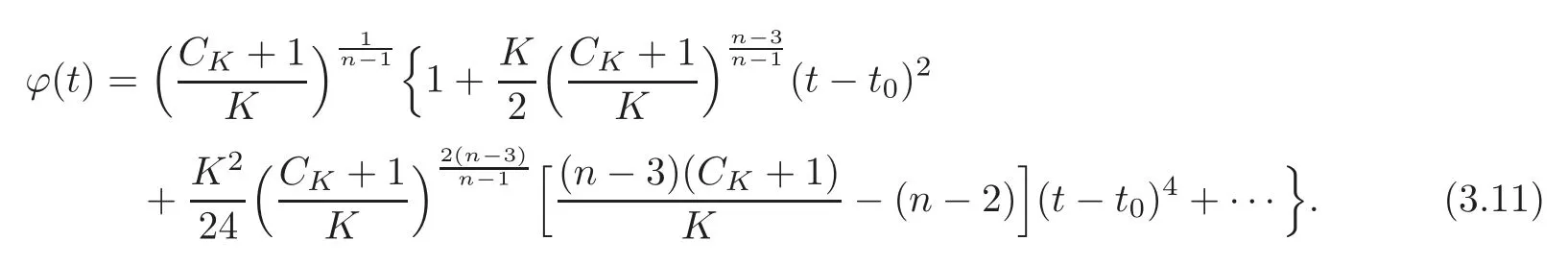
ProofSimilar to Lemma 3.2,we can compute the 2kthorder derivatives near the minimum

For the non-compact hypersurface,we also have the asymptotic expansion ofϕnear infinity.

Lemma 3.4Up to time translation,the asymptotic expansion of ϕ(t)for K <0and CK=−1in Theorem3.3near−∞is given by

Here,f,g are given by

and

where

ProofBy expanding the integrand in Theorem 3.3,we get

Note that the integral in the first line gives us an undetermined constant.Up to a translation oft,we can take that constant to be 0.Letwe can compute that

3.2 Finite volume of the noncompact hypersurfaces

For the hypersurface described in Theorem 3.3 whenCK=−1,we will show that its“surface area” and “volume” of the region enclosed by the hypersurface are indeed finite.

Before the proof,we introduce the following notations.LetVn(r) denote the volume of ann-dimensional ball of radiusr,andSn(r) denote the area of ann-dimensional sphere of radiusr.It is well-known that

Theorem 3.4The surface area of the hypersurface in Theorem3.3when CK=−1is finite.Moreover,the volume of the region enclosed by the hypersurface and the horizontal disk at the end of the hypersurface is also finite.

ProofThe surface area of the rotational hypersurface is

Here,t=t0is the point whereϕ(t) reaches its maximum.Without loss of generality,we can taket0=0 sinceϕ(t) is invariant under translation,namely

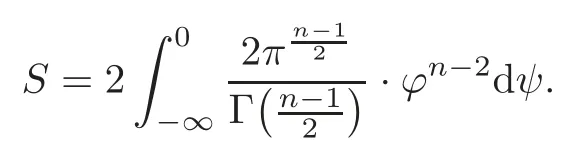
From Theorem 3.3,we know thatϕ′→0 ast→−∞,which also impliesψ′→1 sinceϕ′2+ψ′2=1.

So,we know that ast→−∞,

Consider

Let ord(S) be the order ofS(t) in terms of |t|,namelyS(t)=O(|t|ord(S)).

From Theorem 3.3,we know that the order of the integral in (3.6) is,which indicates that the order of |t| in terms ofϕis. Therefore,the order ofϕin terms of |t| is

Then,we get

Sincen>3,we know that

Therefore,the surface area of this non-compact hypersurface is finite.

Similarly,we can derive the expression of the volume of the enclosed region

Consider

Then we get

Whenn>3,we know that

Clearly,it indicates that the integral converges ast→−∞,and thus the volume is also finite.

Remark 3.4We also compute the approximate value of the volume of the enclosed region and the surface area of this hypersurface whenn=4 andK=1 by Mathematica,which are 1.82 and 19.74,respectively.

3.3 A comparison theorem

From (3.6),we know that the value ofϕ(t) for a given value oftis dependent on the Gauss curvatureK.When the Gauss curvature is a constantK,letϕKdenote the solution to (3.6)described in Theorems 3.2 or 3.3 andψKdenote the corresponding height function.We would like to study the behavior of the solutionϕKwhenKchanges.

In the following theorem,we show that forK >0,the value ofϕKat a fixed heightψK=ydecreases asKincreases if the maximum ofϕKis fixed.Geometrically the generating curve drops faster to the axis of rotation for greater positive Gauss curvature.

Theorem 3.5Take a,b∈Rand a >b>0.Assume that both ϕaand ϕbobtain the same maximum at t=t0,namely ϕa(t0)=ϕb(t0)=ϕmax=C.We also assume that on a small interval D=[t0,t0+δ],both ϕaand ϕbare monotonically decreasing,and ψaand ψbare increasing.Then∀y∈ψa(D)∪ψb(D),we get

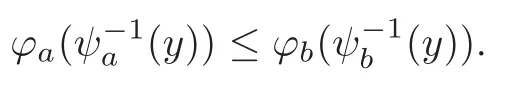
ProofFrom Theorem 3.1,we get

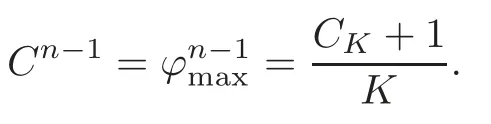
Recall thatϕ′2+ψ′2=1 and the expression ofϕ′in (3.5),we get

Thus,we have

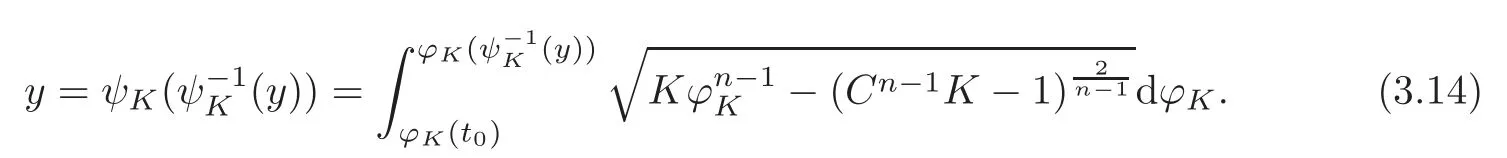
Obviously,we know that the integrandincreases as|K| increases.

Therefore,for a fixed maximumϕa(t0)=ϕb(t0)=Cand negativeϕ′,we must haveϕa(ψ−1a(y))≤ϕb(ψ−1b(y)) to make sure that the left side of (3.14) remains the same.

Similarly,we propose a parallel theorem forK <0.In this case,the generating curve stays further away from the axis of rotation when |K| increases.

Theorem 3.6Take a,b∈Rand0>a >b.Assume that both ϕaand ϕbobtain the same minimum at t=t0,namely ϕa(t0)=ϕb(t0)=ϕmin=C.We also assume that on a small interval D=[t0,t0+δ],both ϕaand ϕbare monotonically increasing,and ψaand ψbare increasing.Then∀y∈ψa(D)∪ψb(D),we get

ProofFirst consider the case whereC=ϕmin≠0.

Similarly to Theorem 3.5,we get

Thus,we have

From Theorem 3.5,we know that the integrandincreases as|K| increase.

Therefore,for a fixed minimumϕa(t0)=ϕb(t0)=Cand positiveϕ′,we must haveϕa(ψ−1a(y))≤ϕb(ψ−1b(y)) to make sure that the left side of (3.15) remains the same.

WhenC=ϕmin=0,thenCKwill be a constant that is independent ofK.In this case,the proof is exactly the same.

AcknowledgementsWe would like to thank Robert Bryant for valuable comments on solving the equations.We also thank Harold Rosenberg for the information on Montiel and Ros’work on the rigidity of compact embedded hypersurfaces with constantr-mean curvature.Our gratitude also goes to Ao Sun and Renato Bettiol,who gave many suggestions on the presentation of this paper.Finally we thank Peking University for providing financial support for the first author.