Ground States of K-component Coupled Nonlinear Schrödinger Equations with Inverse-square Potential∗
2022-07-08PengCHENHuimaoCHENXianhuaTANG
Peng CHEN Huimao CHEN Xianhua TANG
1Three Gorges Mathematical Research Center,China Three Gorges University,Yichang,Hubei 443002,China;College of Science,China Three Gorges University,Yichang,Hubei 443002,China.E-mail: pengchen729@sina.com
2College of Science,China Three Gorges University,Yichang,Hubei 443002,China.E-mail: huimaochen@yeah.net
3School of Mathematics and Statistics,Central South University,Changsha,Hunan 410083,China.E-mail: tangxh@mail.edu.cn
Abstract In this paper,the authors study ground states for a class of K-component coupled nonlinear Schrödinger equations with a sign-changing potential which is periodic or asymptotically periodic.The resulting problem engages three major difficulties: One is that the associated functional is strongly indefinite,the second is that,due to the asymptotically periodic assumption,the associated functional loses the ZN-translation invariance,many effective methods for periodic problems cannot be applied to asymptotically periodic ones.The third difficulty is singular potential,which does not belong to the Kato’s class.These enable them to develop a direct approach and new tricks to overcome the difficulties caused by singularity and the dropping of periodicity of potential.
Keywords Schrödinger equations,Ground states,Strongly indefinite functionals,Non-Nehari manifold method.
1 Introduction
In this paper,we study standing waves for the following system of time-dependent nonlinear Schrödinger equations:

where Φ=(φ1,φ2,···,φK),µi(i=1,2,···,K) are non-negative constants.φj(t,x)(j=1,2,···,K) are the complex valued envelope functions.Suppose thatf(x,eiθΦ)=f(x,Φ) forθ∈[0,2π],x∈RN{0},N≥3.We will look for standing waves of the form
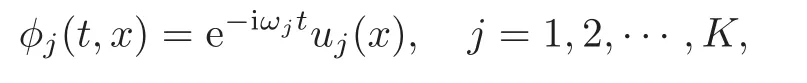
which propagate without changing their shape and thus have a soliton-like behavior.It is well known that solutions of (1.1) are related to the solitary waves of the Gross-Pitaevskii equations,which have applications in many physical models,such as in nonlinear optics and in Bose-Einstein condensates for multi-species condensates(see[4,26])and the references therein.In general,the above coupled nonlinear Schrödinger system leads to the elliptic system
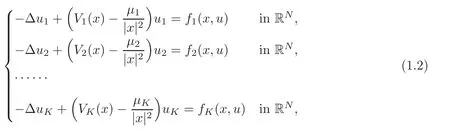
whereN≥3,fi(x,u)=∂uiF(x,u) withu=(u1,u2,···,uK):RN→RK.
Whenµi=0 (i=1,2,···,K),(1.2) reduces to
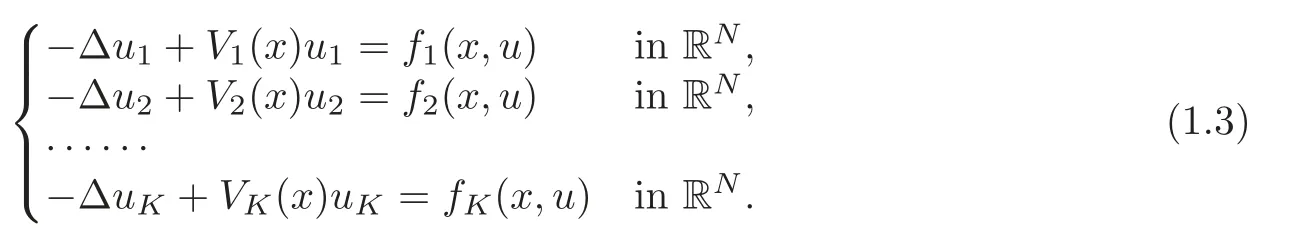
In the past fifteen years,the two-coupled case of (1.3)(i.e.,k=2)has been studied extensively in the literature[5,11–12,14–15,17,21–25,28–29,37–40]and the references therein.By using variational methods,Lyapunov-Schmidt reduction methods or bifurcation methods,various theorems,about the existence,multiplicity and qualitative properties of nontrivial solutions of the two-coupled elliptic systems similar to (1.3),have been established in the literature under various assumptions.However,there are very few works aboutk≥3 in the context [18–19,35–36].It is worth to mention that most of them focused on the case thatVis non-negative constant or function,compared to this case,it is more difficult to consider the case thatVis a sign-changing function to which the energy functional corresponding has the strongly indefinite structure.Very recently,Mederski [20]considered (1.3) and obtained the existence of ground state solution for the case of periodic potential by applying a new linking-type result involving the Nehari-Pankov manifold.
Forµi≠0,is called inverse square potential or Hardy potential which arises in many other areas such as quantum mechanics,nuclear,molecular physics and quantum cosmology.From the mathematical point of view,the inverse square potential is critical: Indeed,it has the same homogeneity as the Laplacian and does not belong to the Kato’s class,hence it cannot be regarded as a lower order perturbation term of second order operator,which may result in the change of the essential spectrum of the operator.Moreover,any nontrivial solutions of system(1.2)are singular atx=0 ifµ≠0.Since the appearance of inverse square potential,compared with system (1.3),system (1.2) becomes more complicated to deal with and therefore we have to face more difficulties.As far as we know,it seems that there are no existence results of solution for system (1.2),hence,it makes sense for us to investigate system (1.2) thoroughly.Due to the special physical importance and the above facts,in the present paper,we will study the existence and some properties of solutions of system (1.2).
As a motivation,we recall that there are many of articles concerning the nonlinear Schrödinger equations with the inverse square potentials

see for example,[1–4,6–9,16,27–28]and the references therein.These authors studied the existence of positive solutions,nodal solutions,multiple solutions and ground state solutions under suitable assumptions.Most of them focused on the case thatVis non-negative constant or function in which the energy functional corresponding to(1.4)has the mountain pass structure.Only very recently,Guo and Mederski[10]studied the case thatVis a general periodic function,possibly sign-changing,and the corresponding energy functional may be strongly indefinite.Combining Nehari manifold technique (see [22–23,29]) and linking argument,they proved the existence of ground state solutions for the caseµ≥0 and the non-existence of ground state solutions was explored for the caseµi<0.Furthermore,some asymptotical behavior of ground state solutions are derived.
Inspired by the aforementioned works,we are going to consider two situations in the present paper: Periodic case and asymptotically periodic case.Our aim is to find ground states for(1.2)on some suitable manifold,one difficulty is that the associated functional is strongly indefinite,i.e.,its quadratic part is respectively coercive and anti-coercive in infinitely dimensional subspace of the energy space.To tackle this difficulty,we adapt the properties of the spectrum of the corresponding opertor which had been analysed in [40],it is convenient to decompose the functional spaceL2into a direct sum of two subspacesE+andE−(Eis defined in Section 2),one of which is infinite dimensional.
Another difficulty is lack of periodic assumption on potential.As a result,neither the periodic translation technique nor the compact inclusion method can be adapted.In this case,the functional loses the ZN-translation invariance.For the above reasons,many effective methods for periodic problems cannot be applied to asymptotically periodic ones.To the best of our knowledge,there are no results on the existence of ground state solutions to(1.2)whenViis not periodic.In this paper,we find new tricks to overcome the difficulties caused by getting rid of periodicity condition.
The last difficulty is singular potential,which does not belong to the Kato’s class.This enables us to develop a direct approach and new tricks to overcome the difficulties caused by singularity.We find a new method to overcome the difficulty caused by the non-compactness of the embeddingH1(RN)→L2(BR(0),|x|−2dx).Our treatments presented in the paper differ from those in [10]and other existing literature.
In this paper,we further develop the non-Nehari method in [32–33]which is completely different from the one of Szulkin-Weth [31]and Mederski [20]to find ground state solution of Nehari-Pankov type for (1.2).For the asymptotically periodic case,a nontrivial solution is obtained by using a generalized linking theorem and comparing with a ground state solution of the periodic problem associated with (1.2).More precisely,we will prove that system (1.2)possesses a ground state solution via variational methods for sufficiently smallµ≥0,and provide the comparison of the energy of ground state solutions for the caseµ >0 andµ=0.Moreover,we also give the convergence property of ground state solutions asµ→0+.
To simplify notation,we set
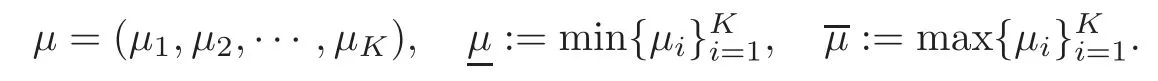
For the sake of convenience,letEbe the Hilbert spaces with an orthogonal decompositionE=E−⊕E+,and let Iµdenote the energy functional of system (1.2),whereEand Iµwill be defined in Section 2.A ground state solution stands for a critical point being a minimizer of Iµon the Nehari-Pankov manifold introduced in [22–23],

the set Nµis a natural constraint and it contains all nontrivial critical points,any ground state solution is a nontrivial critical point with the least energy of Iµ.
Letl0be a positive constant(l0will be given later in (2.3)).Now,we are ready to state the main results of the present paper as follows.
1.1 Periodic potential
(V1) Fori=1,2,···,K,Vi∈C(RN)∩L∞(RN) is ZN-periodic and

for allx∈RN;
(F1)fi:RN×RK→R is measurable,ZN-periodic inx∈RNand continuous inu∈RKfor a.e.x∈RN.Moreoverf=(f1,f2,···,fK)=∂uF,whereF: RN×RK→R is differentiable with respect to the second variableu∈RKandF(x,0)=0 for a.e.x∈RN;
(F2) there exist constantsC >0 and 2 (F3)f(x,u)=o(u) as |u|→0 uniformly inx∈RN; (F5) for allκ≥0,u,v∈RK, (F6)∂uF(x,·) is ofC1class for a.e.x∈RNand there existb1,b2>0 and 1 Theorem 1.1Assume that(V1),(F1)–(F5)are satisfied andthensystem(1.2)has a ground state,i.e.,it has at least a solution uµ∈E such thatIµ(uµ)= Theorem 1.2Assume that(V1),(F1)–(F5)are satisfied and0≤Letuµbe a ground state solution ofIµand u0be a ground state solution ofI0.Then (i)there exist t>0and w∈E−such that tuµ+w∈N0and (ii)there exist t>0and w∈E−such that tu0+w∈Nµand Theorem 1.3Assume that(V1),(F1)–(F5)and(F6)are satisfied,let uµbe a ground state solution ofIµand u0be a ground state solution ofI0.Then (i)there holds (ii)for any sequence{µ(n)},there exists a subsequence uµ(n)such that (V1’)Vi(x)=Ui(x)+Wi(x),i=1,2,···,K,whereUi∈C(RN)∩L∞(RN) is ZN-periodic and for allx∈RN,Wi∈C(RN) andMoreover, (F1’)fi(x,u)=gi(x,u)+hi(x,u),gi:RN×RK→R is measurable,ZN-periodic inx∈RNand continuous inu∈RKfor a.e.x∈RN,gi(x,u)=o(u) as |u|→0,uniformly inx∈RN; (F5’)∂uG=(g1,g2,···,gK),whereGsatisfies that for allκ≥0,u,v∈RK, Furthermore,∂uH=(h1,h2,···,hK) andHsatisfies that whereai∈C(RN),Moreover, Theorem 1.4Assume that(V1’),(F1’),(F2)–(F4),(F5’)are satisfied and0≤µ≤µ Theorem 1.5Assume that(V1’),(F1’),(F2)–(F4),(F5’)are satisfied andLet uµbe a ground state solution ofIµand u0be a ground state solution ofI0.Then (i)there exist t>0and w∈E−such that tuµ+w∈N0and (ii)there exist t>0and w∈E−such that tu0+w∈Nµand Theorem 1.6Assume that(V1’),(F1’),(F2)–(F4),(F5’),(F6)are satisfied,let uµbe a ground state solution ofIµand u0be a ground state solution ofI0.Then (i)there holds (ii)for any sequence{µ(n)},there exists a subsequence uµ(n)such that The present paper is organized as follows.Section 2 is dedicated to the variational form associated with problem (1.2).We recall the abstract linking theorem in [13],which is going to be used to prove the existence of solution in periodic case,as well as in the asymptotically periodic case.Some preliminaries are introduced in Section 3.Section 4 is dedicated to the periodic case.In order to do so,exploiting the profile of spectrum presented by the associated operator,we decompose the spaceEin appropriate subspaces for the linking structure.Subsequently,the requirements of the abstract result are verified: compactness,linking geometry and boundedness of Cerami sequences for the functional associated with problem(1.2).Section 5 is dedicated to asymptotically periodic case.Our greatest challenge in the asymptotically periodic case is the functional loses the ZN-translation invariance,many effective methods for periodic problems cannot be applied to asymptotically periodic ones. Let Ai=−∆+Vi,here and in what followsi=1,2,···,K.Then Aiare self-adjoint inL2(RN) with domain D(Ai)=H2(RN).Let {ℇi(λ):−∞≤λ≤∞} and |Ai| be the spectral family and the absolute value of Ai,respectively,and |Ai|12be the square root of Ai.Set Ui=id−ℇi(0)−ℇi(0−).Then Uicommutes with Ai,|Ai| and |Ai|12,and Ai=Ui|Ai| is the polar decomposition of Ai. Let Define and the corresponding norm For anyu∈H,fixingi=1,2,···,K,it is easy to see that Since 0/∈σ(−∆+Vi),the spectral theory asserts that we may find continuous projectionsP+iandPi−ofH1(RN) ontoHi+andHi−,respectively,such thatH1(RN)=Hi+⊕Hi−,then Belshazzar appears in the Old Testament as a Babylonian general and son of Nebuchadnezzar II; according to the Old Testament he was warned of his doom by divine handwriting on the wall that was interpreted by Daniel (6th century BC) (WordNet).Return to place in story. and norms are given by Let Note that anyu∈E:=H1(RN)Kadmits a unique decompositionu=u++u−,where We introduce a new norm onEgiven by Then Our hypotheses imply that Iµ∈C1(E,R) and a standard argument shows that critical points of Iµare solutions of (1.2). Lemma 2.1E is continuously embedded in Lq(RN,RK)and compactly embedded in(RN,RK),where2≤q≤2∗,2≤q′<2∗,2∗is defined in(F2). By Lemma 2.1,there exist positive constantsl0,l1such that Observe that,in view of the Hardy inequality then we have To get the ground state solutions of (1.2),we define the generalized Nehari manifold This type of manifold was first introduced by Pankov[22–23].As is well known that ifuµ≠0 is a critical point of Iµ,thenuµ∈Nµ.The ground state solution will be obtained as a nontrivial critical point of Iµin Nµ.The next section will be used to get such points. Lemma 3.1(see [13])Let X be a real Hilbert space,X=X−⊕X+and X−⊥X+,and let ϕ∈C1(X,R)be of the form Suppose that the following assumptions are satisfied: (A1)ψ∈C1(X,R)is bounded from below and weakly sequentially lower semi-continuous; (A2)ψ′is weakly sequentially continuous; (A3)there exist r >ρ>0,e∈X+with‖e‖=1such that where Then for some c∈[κ,supϕ(Q)],there exists a sequence{un}⊂X satisfying Set Employing a standard argument,one can check easily the following lemma. Lemma 3.2Assume that(V1’),(F1’)and(F2)–(F4),(F5’)are satisfied,thenFµis nonnegative,weakly sequentially lower semicontinuous,andF′µis weakly sequentially continuous. Lemma 3.3Assume that(V1’),(F1’)and(F2)–(F4),(F5’)are satisfied.Then for all κ≥0,u∈E,ζ=(ζ1,ζ2,···,ζK)∈E−, ProofFrom (2.1)–(2.2) and (F5’) we have Using Lemma 3.3,some important corollaries are given as follows,the proof process will be omitted. Corollary 3.1Assume that(V1’),(F1’)and(F2)–(F4),(F5’)are satisfied.Then for u∈Nµ,we have Corollary 3.2Assume that(V1’),(F1’)and(F2)–(F4),(F5’)are satisfied.Then for all u∈E,κ≥0, Lemma 3.4Assume that(V1’),(F1’)and(F2)–(F4),(F5’)are satisfied.Then (i)there exists ρ>0such that ProofSetIt follows from (V1’) that By (V1’) and (F2),there existp∈(2,2∗) andC1>0 such that From Corollary 3.1,we have foru∈Nµ, This shows that there exists aρ>0 such that (i) holds. By Lemma 3.2,Fµ(u)>0 for all (x,u)∈RN×RK,so we have foru∈Nµ, With the help of the preceding two corollaries,an argument similar to the one used in [34]shows that we can now prove the following lemma in the same way as [34]. Lemma 3.5Assume that(V1’),(F1)–(F4)are satisfied.Then for every e∈E+,we havesup Iµ(E−⊕R+e)<∞,and there exists Re>0such that ProofLete∈E+,t≥0 andu=te+u−∈E−⊕R+e.Sinceµi≥0,we have For the proof of the functional I0is standard,see [34].So we omit its details here. Corollary 3.3Assume that(V1’),(F1)–(F4)are satisfied.Let e∈E+with‖e‖=1.Then there exists r0>ρ such thatsup Iµ(∂Q)≤0as r≥r0,where Lemma 3.6Assume that(V1’),(F1)–(F4)are satisfied andThenthere exist a constant cµ∈[Λµ,sup I(Q)]and a sequence{un}⊂E satisfying where Q is defined in(3.3). ProofCombining with Lemmas 3.1–3.2,3.4 and Corollary 3.3,it is easy to verify Lemma 3.6.The proof will be omitted. Lemma 3.7Assume that(V),(F1)–(F4)are satisfied andThenthere exist a constant cµ∈[Λµ,mµ]and a sequence{un}⊂E satisfying ProofThis is a standard result which can be found in [32–33],for the convenience of readers,we give the detailed proof process here.Chooseξk∈Nµsuch that Using Lemma 3.4,we can deriveLetThenek∈E+with‖ek‖=1.Applying Corollary 3.3,there exists a constantrk>max{ρ,‖ξk‖} satisfying sup Iµ(∂Qk)≤0,where Then,by Lemma 3.6,there exist a constantck∈[Λµ,sup Iµ(Qk)]and a sequence {uk,n}n∈N⊂E, In virtue of Corollary 3.1,we get Sinceξk∈Qk,by (3.6) and (3.8) we have Iµ(ξk)=sup Iµ(Qk).Furthermore,by (3.5) and(3.7),we have We can choose {nk}⊂N such that Setuk=uk,nk,k∈N. Then we have Lemma 3.8Assume that(V1’),(F1)–(F4)are satisfied.Then for any u∈EE−,N−∩(E−⊕R+z)≠∅,there exist η(u)>0,ζ(u)∈E−such that η(u)u+ζ(u)∈Nµ. ProofNote thatE−⊕R+u=E−⊕R+u+,then we may assume thatu∈E+.It follows from Lemma 3.5 that there exists a constantR >0 such that Iµ(u)≤0 for anyu∈(E−⊕R+z)BR(0).For sufficiently smalls≥0,we have Iµ(su)>0.Thus,0 In this section,we assume thatVandfare 1-periodic in each ofx1,x2,···,xN,i.e.,(V1)and (F1) are satisfied.In this case,Vi=UiandWi=0. Lemma 4.1Assume that(V1),(F1)–(F4)are satisfied.Then for any{un}⊂E such that and is bounded in E,where ProofChooseM >0 such that |Iµ(n)(un)|≤M.We prove the boundedness of {un}by negation,if the assertion would not hold,then ‖un‖→∞.Denotevn=we have‖vn‖=1.Taking into account Sobolev embedding theorem,there exists a constantC1>0 such that ‖vn‖2≤C1.If it is easy to verify thatv+n→0 inLp(p∈(2,2∗)) by using Lions’ concentration compactness principle.combining(F1) with (F2),we see that there exists a constantCε>0 such that This leads to a contradiction,soδ >0. Without loss of generality,we suppose the existence ofkn∈ZNsuch that Denoteζn(x)=vn(x+kn),then which is a contradiction.Hence the statement of Lemma 4.1 is proved. The following fact is very useful to deal with the Hardy type term and plays a very important role in the proof of the decomposition result.Their proofs are similar to those in [10],which we omit here. Lemma 4.2If|xn|→∞,then for any u∈E, Lemma 4.3Assume thatand let{un}be a bounded(C)cµ-sequence ofIµat level cµ≥0.Then there exists uµ∈E such thatI′µ(uµ)=0,and thereexist a number k∈N∪{0},nontrivial critical points u1,···,ukofI0and k sequences of points xin⊂ZN,1≤i≤k,such that Lemma 4.4Assume that Q∈C(RN×RK,R)and there exist a0,b1,b2>0,p∈(2,2∗)and1 If un⇀u in E,and then un→u in Lq1(RN). Proof of Theorem 1.1In light of Lemma 4.1,there exists a bounded sequence{un}⊂Esatisfying Lemma 3.6.Hence,there exists a constantC2>0 such that ‖un‖2≤C2.Ifthenun→0 inLp,wherep∈(2,2∗).On the other hand,by virtue of (F1) and (F2),forthere exists a constantCε>0 such that Based on the above discussion,we have Thus, which is a contraction.Thenδ >0. Passing to the subsequence,we may assume that there existskn∈ZNsuch that Setζn(x)=un(x+kn),then Due to the periodic assumption ofV(x) andF(x,u),it follows that ‖ζn‖=‖un‖ and Thus,passing to the subsequence,suppose thatζn⇀ζinE,ζn→ζinL2loc,ζn(x)→ζ(x)a.e.on RN.In light of (4.4),we see thatζ≠0.For everyφ∈C∞0(RN),by (2.2),we haveHence,I′µ(ζ)=0,which implies thatζ∈Nµ.Then,Iµ(ζ)≥mµ.On the other way,it follows from (F2),(F3),(F4),Lemmas 3.4,3.7 and Fatou’s lemma that which implies Iµ(uµ)≤mµ.So Iµ(uµ)=mµ=The proof is completed. Next we claim thatuµ≠0.Indeed,forµ=0,by Lemma 3.7 and the concentration compactness arguments,it is easy to prove that I0has a nontrivial ground state solutionu0∈N0such that I0(u0)=m0=Now let us assume thatand consider Observe that,lettnu0+wn∈Q(u0),then passing to a subsequence we may assume thattn→t0,wn⇀w0inE−andandwn(x)→w0(x)a.e.on RN.Hencetnu0+wn⇀t0u0+w0∈Q(u0) by the weak lower semi-continuous of norm,which implies thatQ(z0) is weakly sequentially closed.It follows from Fatou’s lemma that this shows that Iµis weakly sequentially upper semi-continuous.Then Iµattains its maximum inQ(u0).Assume thatt0u0+w0∈Q(u0) such that thent0u0+w0∈Nµ.Therefore by Corollary 3.1,we have similar to the Lemma 4.3,we getun→uµinE,and souµ≠0.The proof is completed. Proof of Theorem 1.2Letuµ∈Nµbe a ground state solution of Iµand 0≤µ≤µ this shows that conclusion (i) holds.Similarly,letu0∈N0be a ground state solution of Iµ.By Lemma 3.8,there existt0>0 andw0∈E−such thatt0u0+w0∈Nµ.Then,by Corollary 3.1 we have which implies that conclusion (ii) holds. Proof of Theorem 1.3Sinceµi≥0,we get by (4.7), and by Lemma 4.1 we have {uµ} is bounded ifµ→0+.We take a sequenceµ(n)→0+and denoteun:=uµ(n).If then by Lions’concentration compactness principle,we getu+n→0 inLpfor 2 then passing to a subsequence,we findu∈Esuch thatu+n(·+yn)→u+inL2locandu+≠0.Moreover,we may assume thatun(·+yn)⇀uinE,un(x+yn)→u(x),u+n(x+yn)→u+(x)a.e.on RN.Lettnun+wn∈N0andtn>0,wn∈E−.By (F6),we havef(x,u)·u−2F(x,u)≥0.Then which contradicts (4.9),thustnis bounded.Then ‖tnu+n‖ and ‖tnu−n+wn‖ are bounded,by the Hölder’s inequality and (2.4) we get Therefore,(4.6),(4.8) and (4.10) imply that conclusion (i) holds. Next,we will verify that (ii) holds.Let {uµ(n)} be a sequence of ground state solutions of Iµ(n),and we take a sequenceµ(n)→0+and denoteun:=uµ(n).It follows from Lemma 4.1 that {un} is bounded,then passing to a subsequence,we may assume thatun⇀u0inE,for 2≤p<2∗andun(x)→u0(x) a.e.on RN. Noting thatVi(x) andf(x,u) are periodic inx,it follows that Thus,we have I′0(u0)=0,which implies thatu0is a nontrivial critical point of I0.We will claim thatu0is a ground state solution of I0.Sinceµ≥0,it is to show thatmµ=Iµ(u) is non-increasing onThen we obtain This implies Thus and It follows from (4.11)–(4.12) thatun→u0inE,which implies that (ii) holds.The proof is completed. In this section,we always assume thatV(x) satisfies (V1’).We define functional Jµas follows Then (V1’),(F1’),(F2)–(F5) imply that Jµ∈C1(E,R) and Similar to Lemma 3.3,we have the following lemma. Lemma 5.1Assume that(V1’),(F1’),(F2)–(F5)are satisfied.Then for all κ≥0,u∈E,ζ=(ζ1,ζ2,···,ζK)∈E−, Lemma 5.2Assume that(V1’),(F1’),(F2)–(F5)are satisfied.Then any sequence{un}⊂E satisfying(4.1)is bounded in E. ProofTo prove the boundedness of {un},arguing by contradiction,we suppose that‖un‖→∞.Letvn=Then ‖vn‖=1 .By Sobolev imbedding theorem,there exists a constantC4>0 such that ‖vn‖2≤C4.Passing to a subsequence,we havevn⇀vin E.There are two possible cases: (i)v=0 and (ii)v≠0. Case (i)v=0,i.e.,vn⇀0 inE.Thenv+n→0 andv−n→0 inLsloc(RN). By (V1’),it is easy to show that If then by Lions’ concentration compactness principle,v+n→0 inLs(RN) for 2 Letηn=Hence,by virtue of (4.1),(5.2)–(5.3) and Corollary 3.2,one can get that This leads to a contradiction,soδ >0.Without loss of generality,we suppose the existence ofkn∈ZNsuch thatDenoteωn(x)=vn(x+kn),then which is a contradiction.Hence the statement of Lemma 5.2 is proved. Case (ii)v≠0.In this case,we can also deduce a contradiction by a standard argument. Cases (i) and (ii) show that {un} is bounded inE. Proof of Theorem 1.4Applying Lemmas 3.7 and 4.1,we deduce that there exists a bounded sequence {un}⊂Esatisfying (3.4).Passing to a subsequence,we haveun⇀uinE.Next,we proveu≠0. Arguing by contradiction,suppose thatu=0,i.e.,un⇀0 inE,and soun⇀0 inLsloc(RN),2≤s<2∗andun→0 a.e.on RN.By (V1’),(F1’) and (F5’),it is easy to show that and Note that and From (5.5)–(5.8),one can get that Analogous to the proof of Theorem 1.2,we can prove that there existskn∈ZNsuch that Denotevn(x)=vn(x+kn),then Passing to a subsequence,we havevn⇀vinE,vn→vinLsloc(RN),2≤s <2∗andvn→va.e.on RN.Obviously,(5.10)implies thatv≠0.SinceUi(x) andgi(x,u) are periodic inx,by(5.9),we have In the same way as the last part of the proof of Theorem 1.2,we can prove that J′µ(v)=0 and Jµ(v)≤cµ. It is easy to show thatv+≠0.By Lemma 3.8,there existκ0=κ(v)>0 andw0=w(v)∈E−such thatκ0v+w0∈Nµ,and so Iµ(κ0v+w0)≥m. Hence,from the fact thatH(x,u)−forwe have sincev(x)0 forThis contradiction implies thatu≠0.In the same way as the last part of the proof of Theorem 1.2,we can certify that I′µ(u)=0 andThis shows thatu∈Eis a solution to (1.2) withThe proof is completed. Similar to the proofs of Theorems 1.2–1.3,we can prove Theorems 1.5–1.6,we omit the proof process. AcknowledgementThe authors would like to thank the anonymous reviewers for thelp and thoughtful suggestions that have helped to improve this paper substantially.

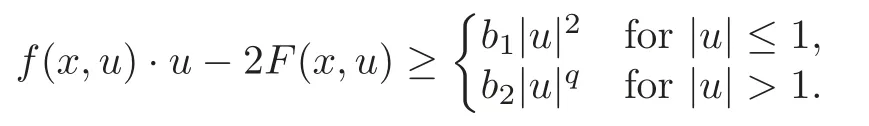
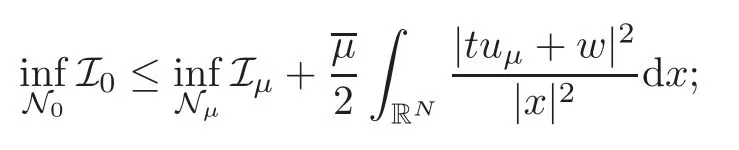
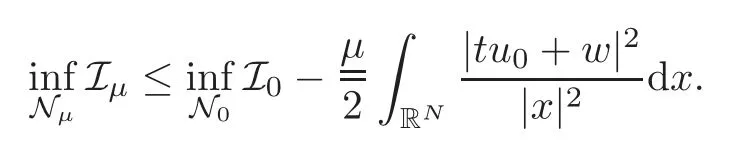
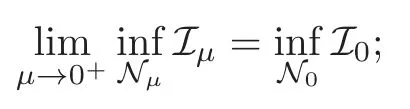

1.2 Asymptotically periodic potential
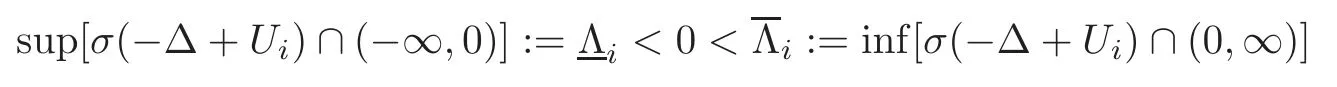
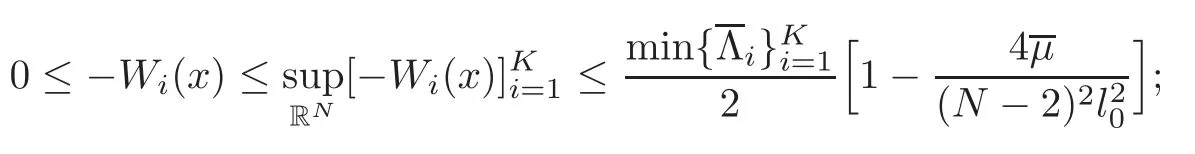


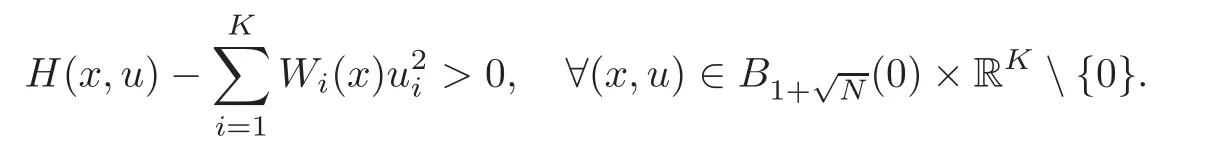


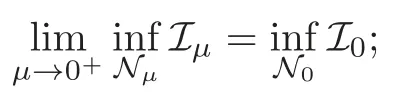
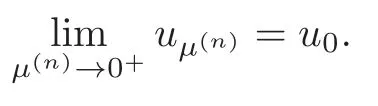
2 Variational Structure
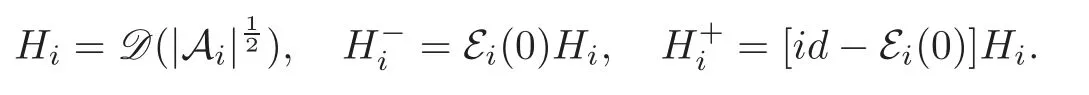


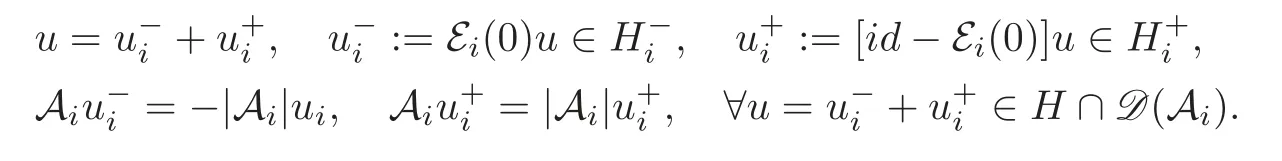
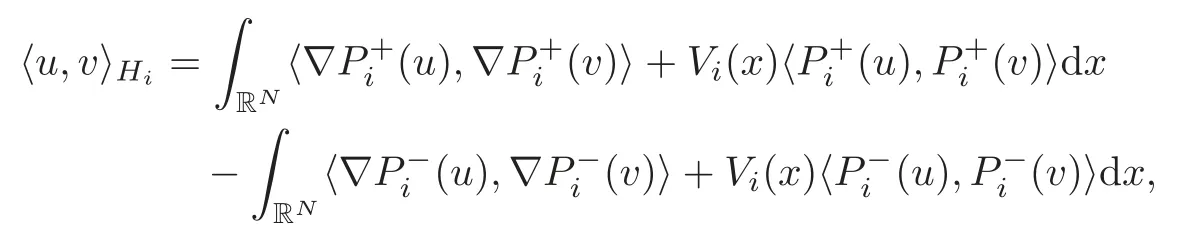

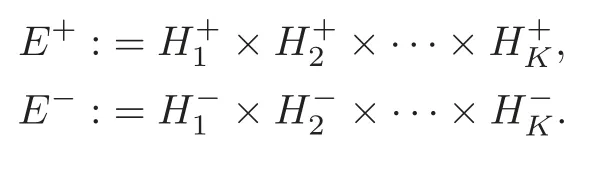
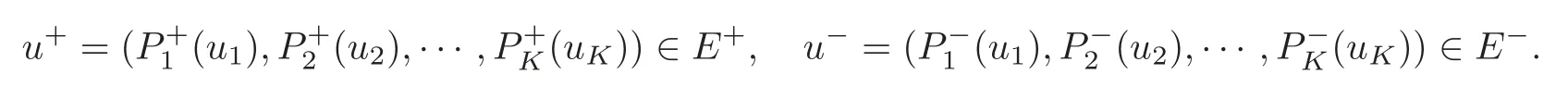

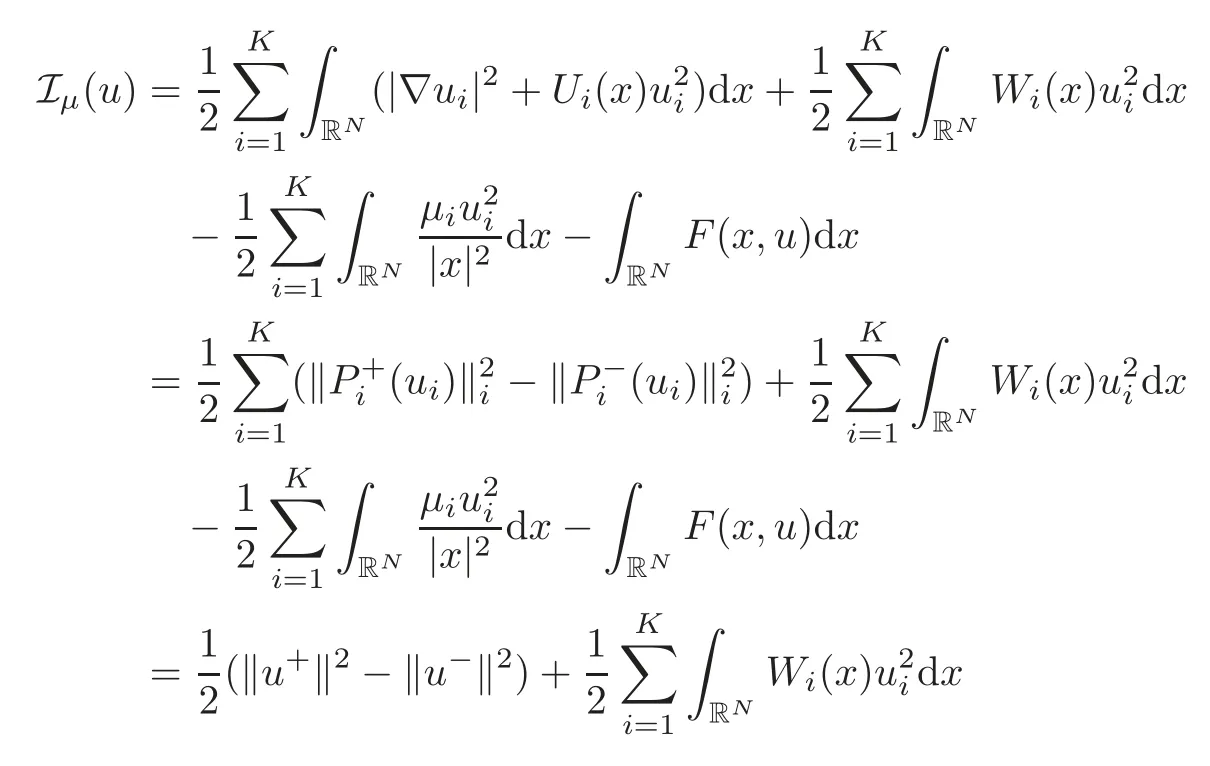
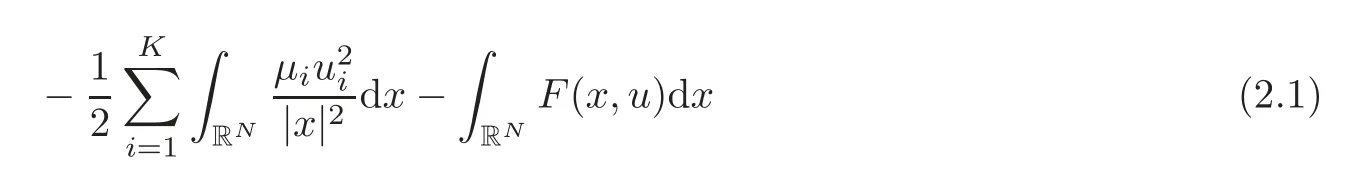
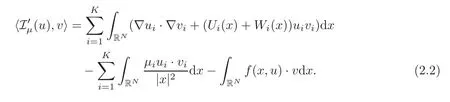

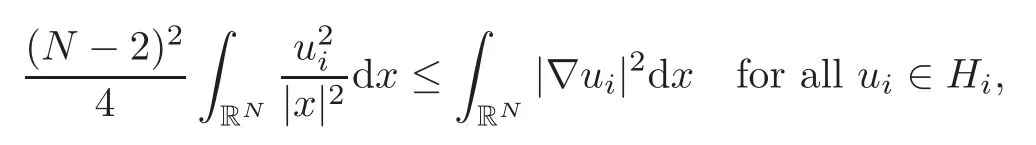

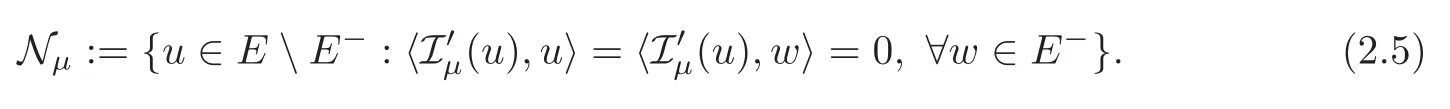
3 Preliminaries
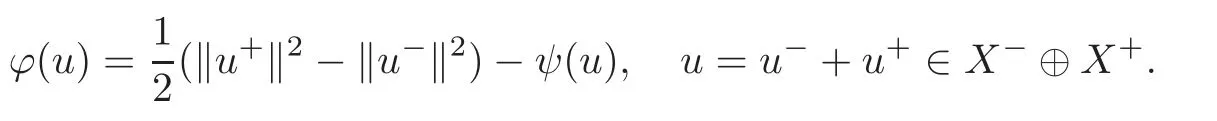
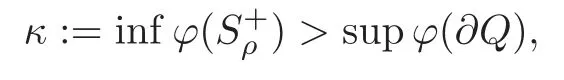
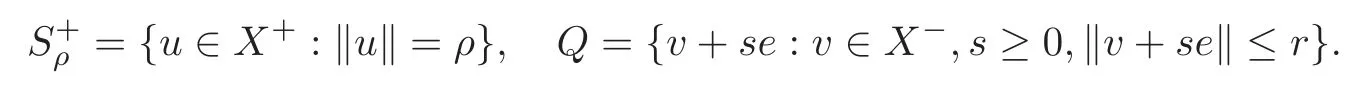
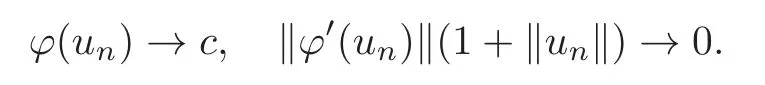
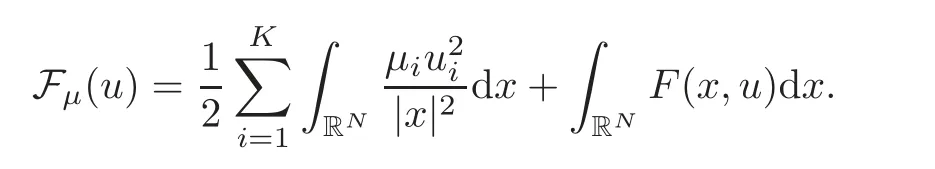

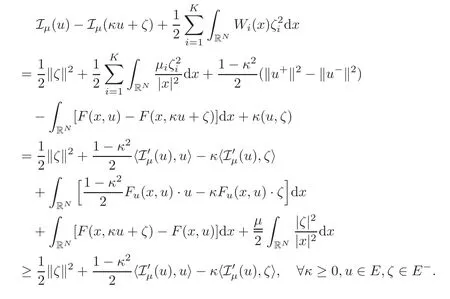
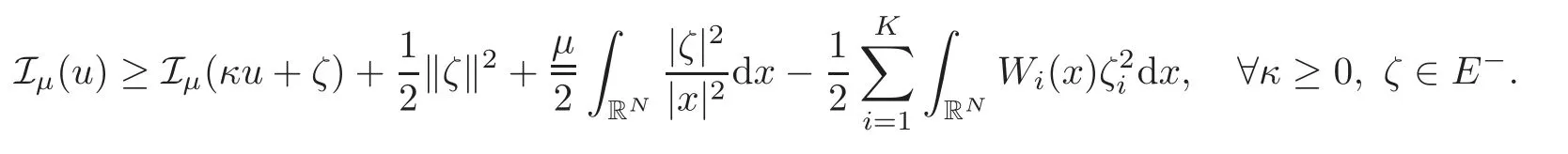


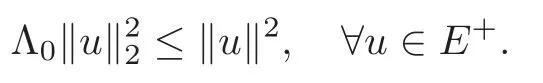
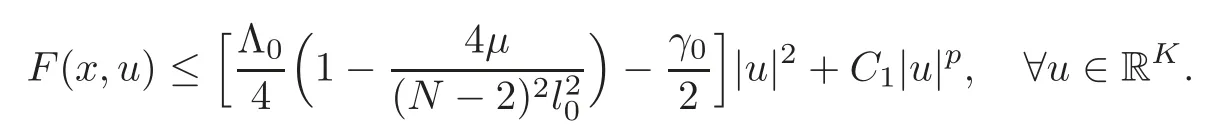
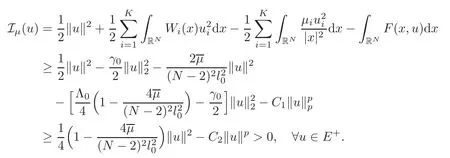
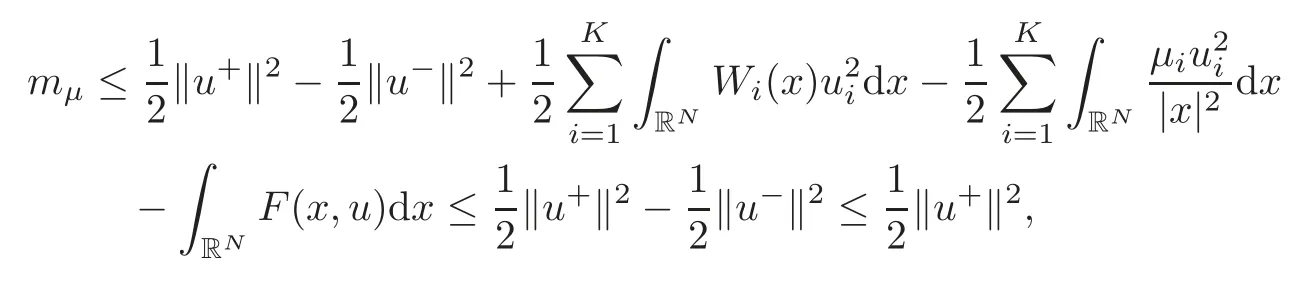


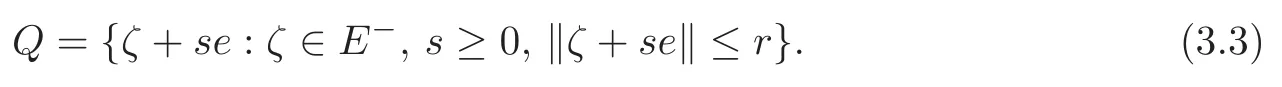
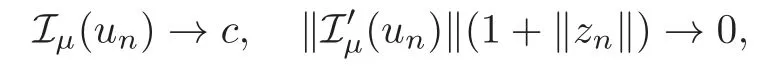
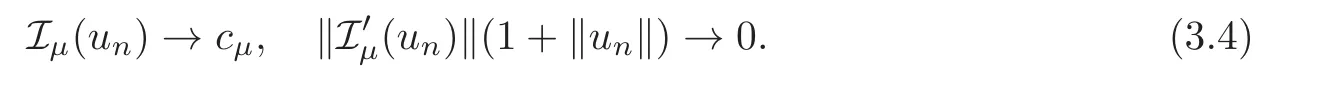

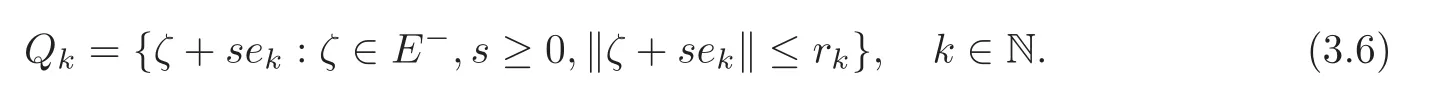

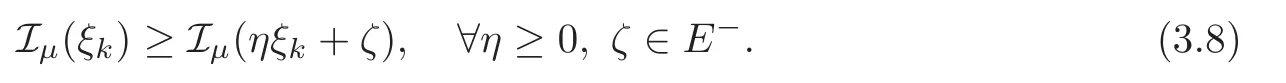
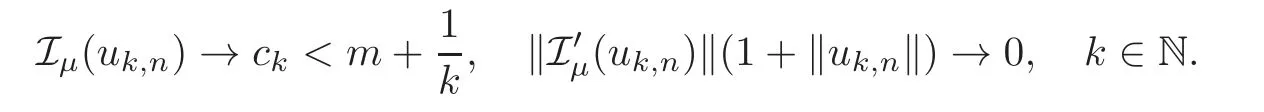
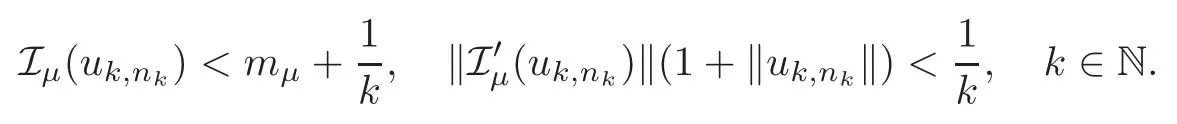
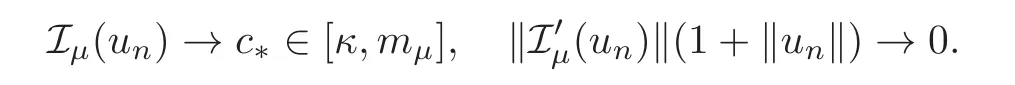
4 Periodic Case
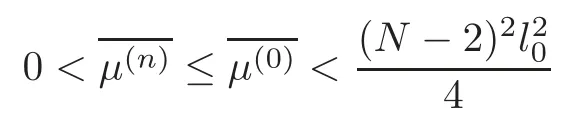

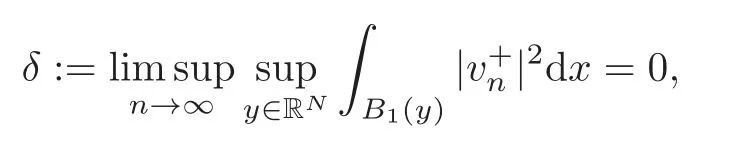
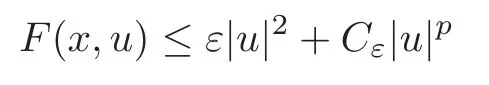


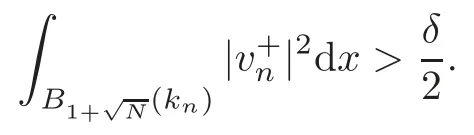

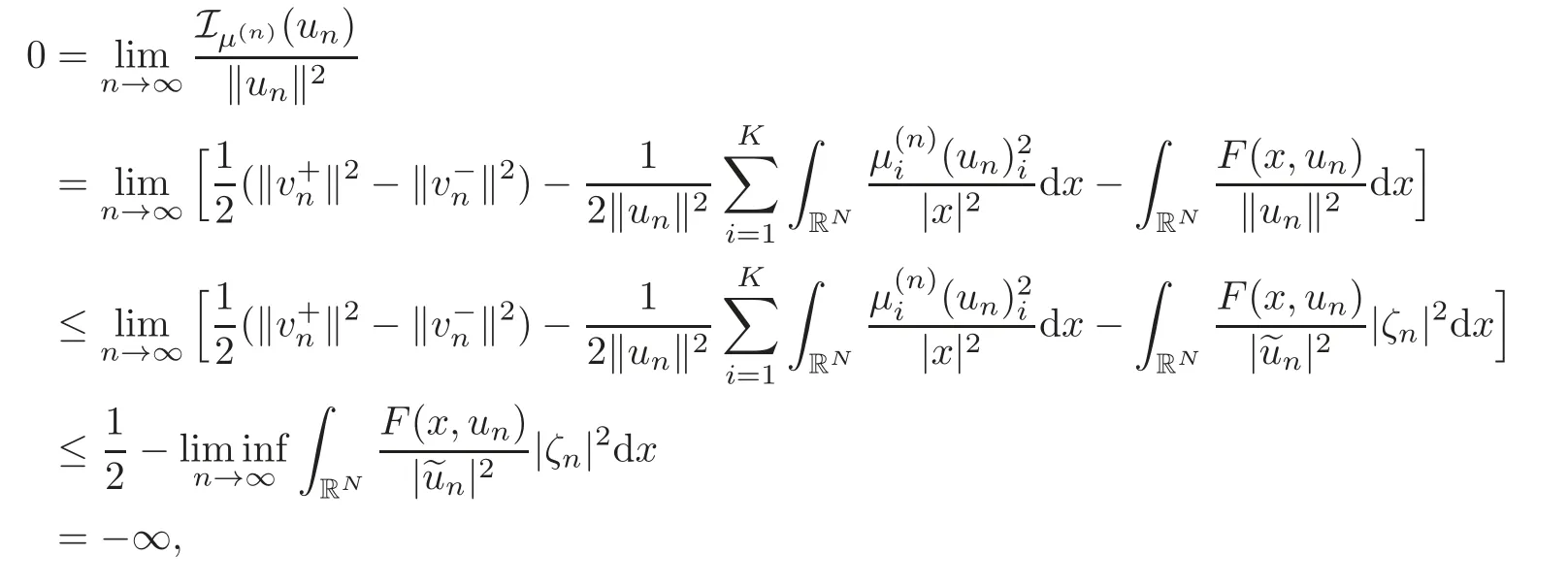
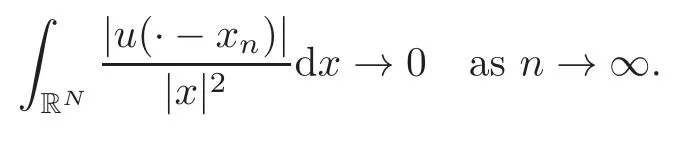

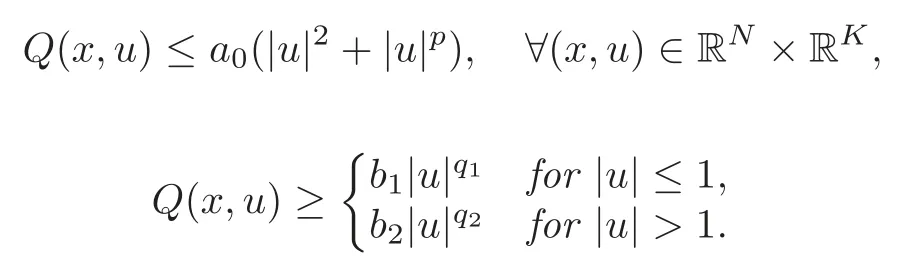
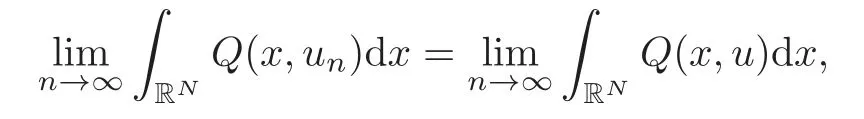

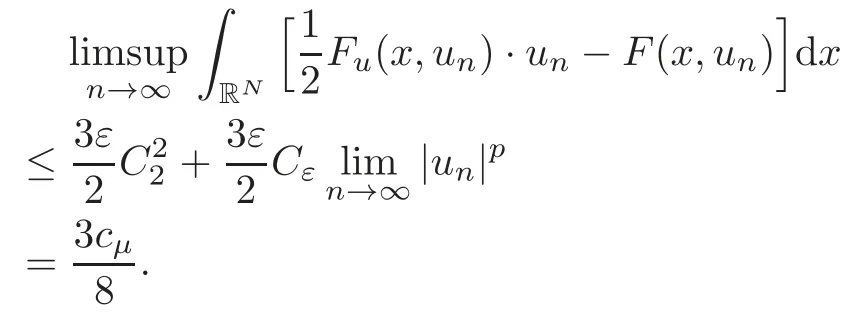
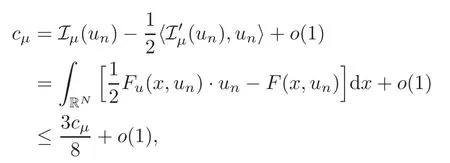



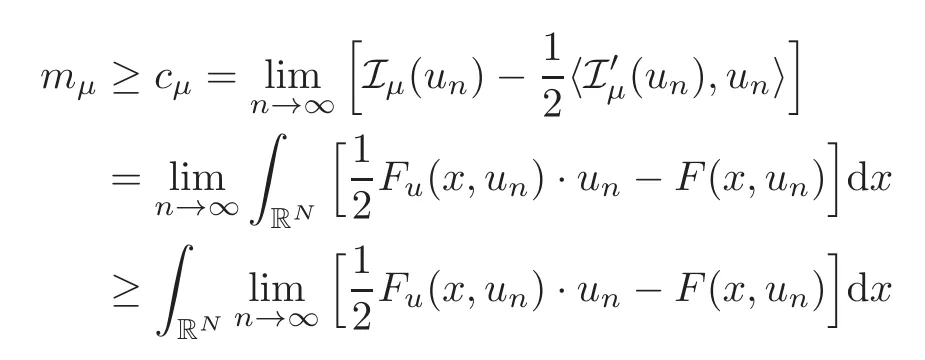
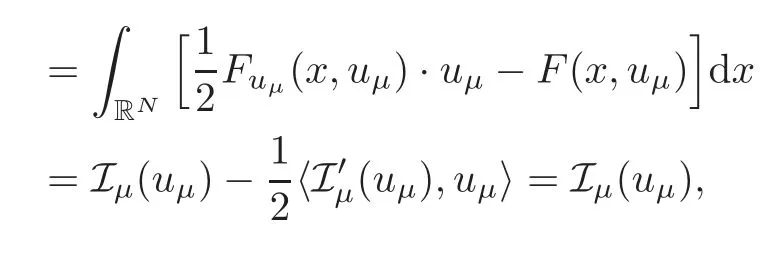
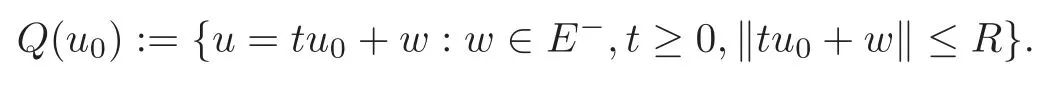

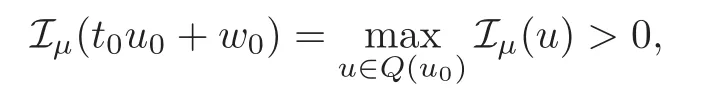
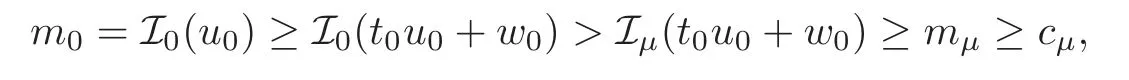




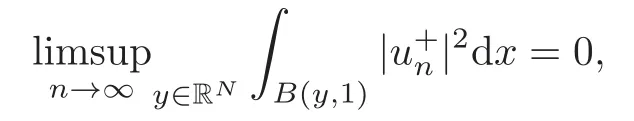
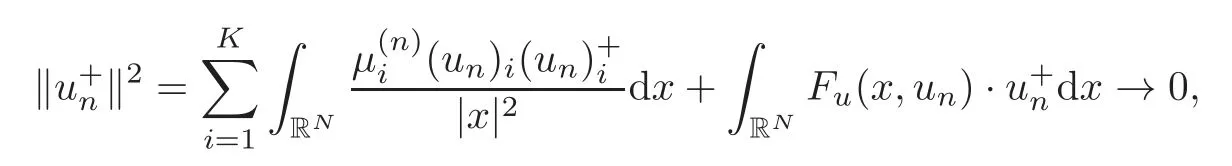
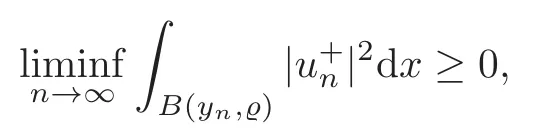
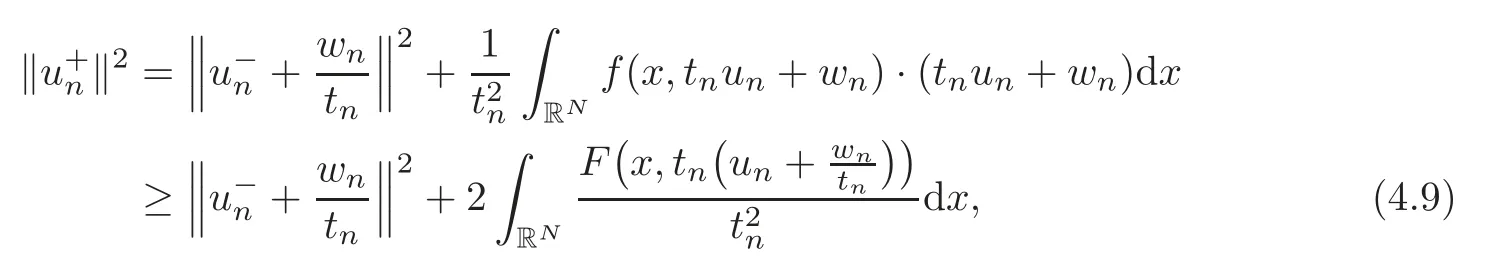
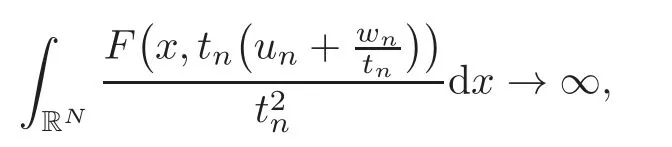


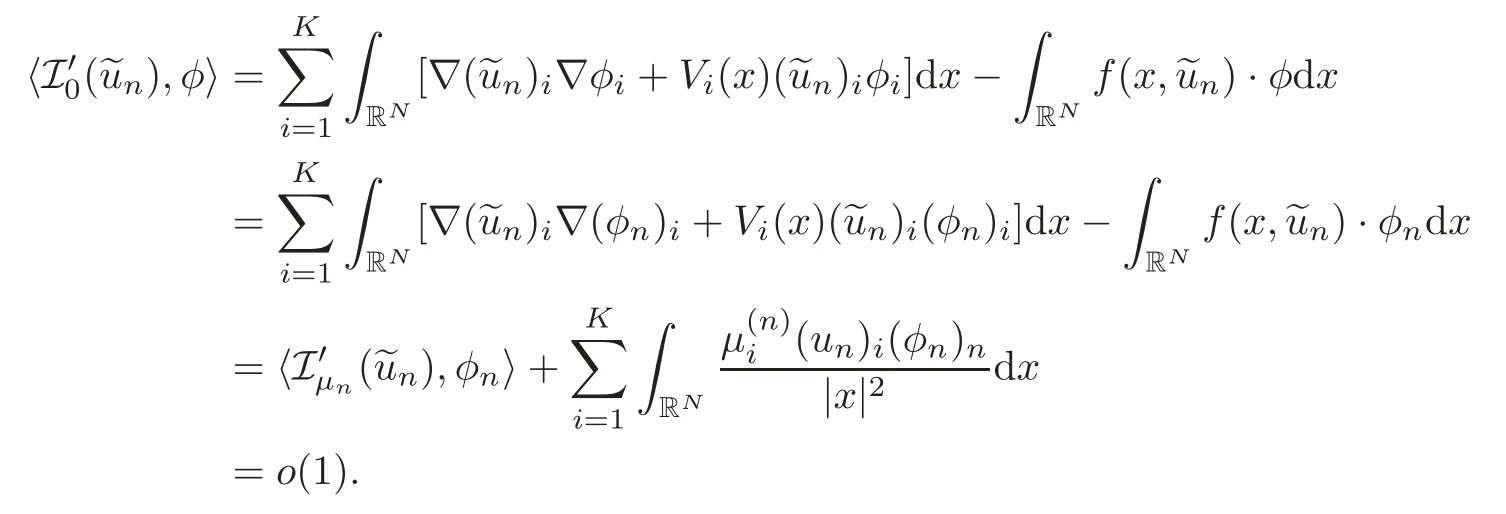




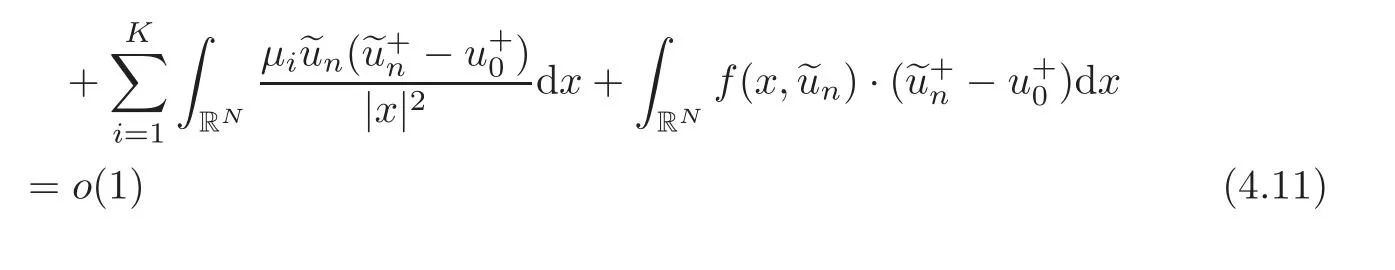
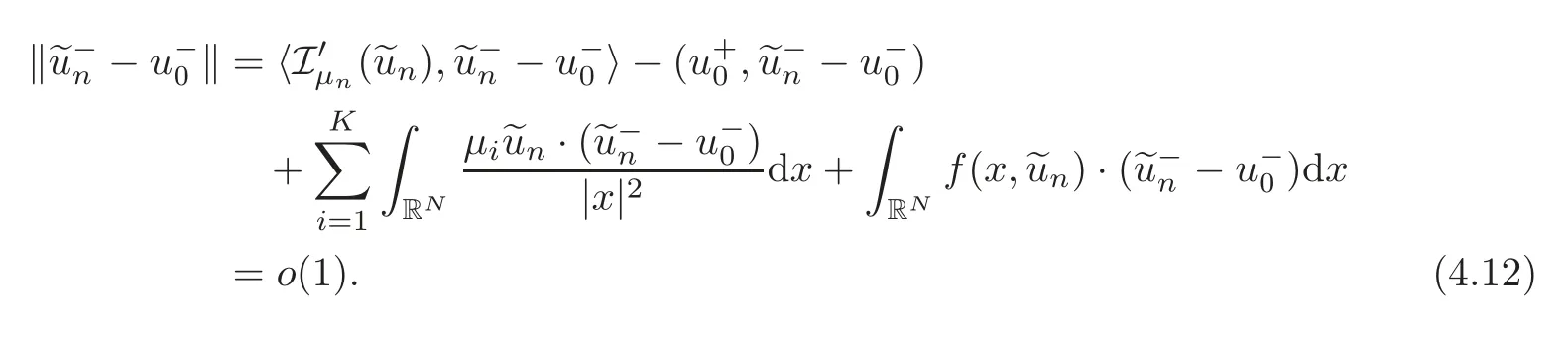
5 Asymptotically Periodic Case
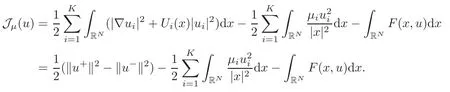




0,there existsCε>0 such that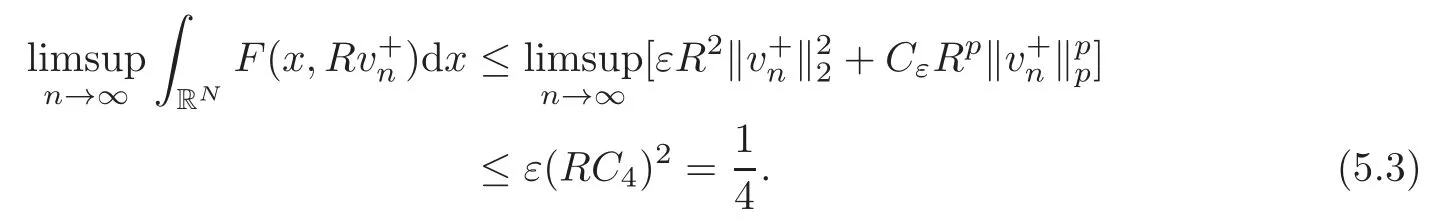
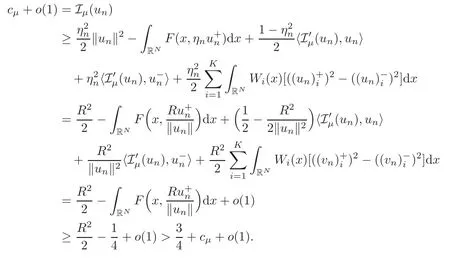

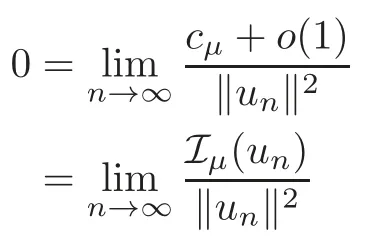
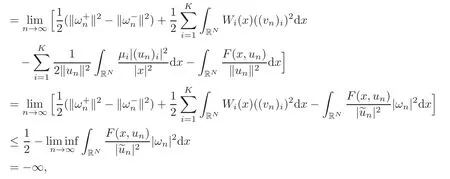

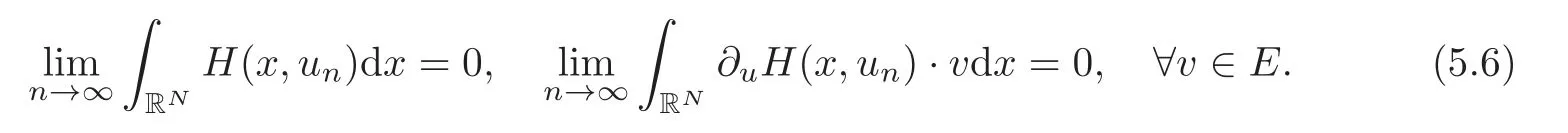
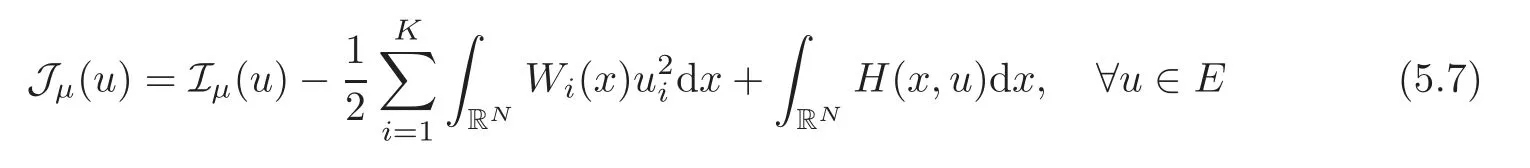
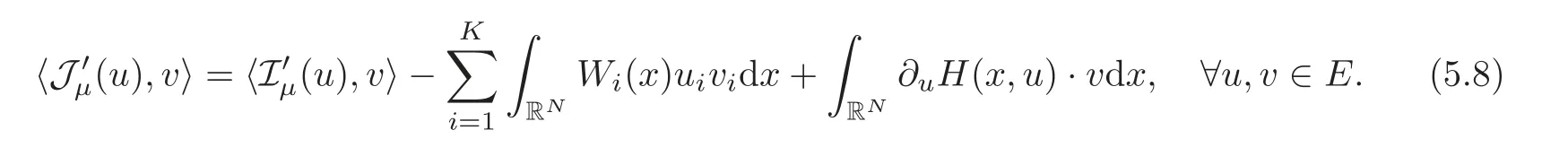



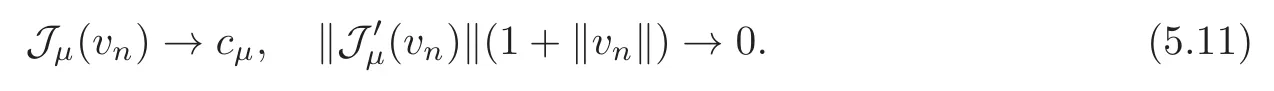
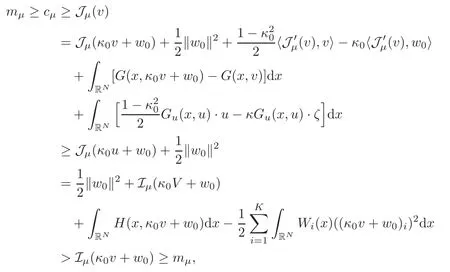
杂志排行
Chinese Annals of Mathematics,Series B的其它文章
- Rotational Hypersurfaces with Constant Gauss-Kronecker Curvature
- A Note on the Indirect Controls for a Coupled System of Wave Equations∗
- A Generalization of Lappan’s Theorem to Higher Dimensional Complex Projective Space∗
- Cartan’s Second Main Theorem and Mason’s Theorem for Jackson Difference Operator∗
- Products of Toeplitz and Hankel Operators on Fock-Sobolev Spaces∗
- On a Supercongruence Conjecture of Z.-W.Sun∗
