A Note on the Indirect Controls for a Coupled System of Wave Equations∗
2022-07-08TatsienLIBopengRAO
Tatsien LI Bopeng RAO
1School of Mathematical Sciences,Fudan University,Shanghai 200433,China;Shanghai Key Laboratory for Contemporary Applied Mathematic,Shanghai 200433,China;Nonlinear Mathematical Modeling and Methods Laboratory,Shanghai 200433,China.E-mail: dqli@fudan.edu.cn
2Corresponding author.Institut de Recherche Math´ematique Avanc´ee,Universit´e de Strasbourg,67084 Strasbourg,France.E-mail: bopeng.rao@math.unistra.fr
Abstract By a procedure of successive projections,the authors decompose a coupled system of wave equations into a sequence of sub-systems.Then,they can clarify the indirect controls and the total number of controls.Moreover,the authors give a uniqueness theorem of solution to the system of wave equations under Kalman’s rank condition.
Keywords Indirect controls,Approximate controllability,Coupled system of wave equations
1 Introduction
Let Ω ⊂Rnbe a bounded domain with smooth boundary Γ.Consider the following system for the variableU=(u(1),···,u(N))T:

whereAis a matrix of orderNandDis a matrix of orderN×M.
Obviously,system (1.1) is controlled by the controlsHdirectly acted on the boundary,and also implicitly influenced by the interaction between the equations.It is well-known that when rank(D) is necessary(and even sufficient in some special situations) for the approximate boundary controllability of system(1.1)(see [7]).This shows that the coupling termAUplays an important role for the approximate boundary controllability.It seems that rank(D,AD,···,AN−1D),called the total number of controls in [8],is a good indicator for the action of the coupling matrixAwith the boundary control matrixD.Since rank(D)is the number of boundary controlsH,it is natural to name rank(D,AD,···,AN−1D)−rank(D) as the number of indirect controls,but we did not see what are these(internal or boundary)controls,nor how they intervene into the system. In this paper,we try to explain the meaning of indirect controls and the mechanism of their roles.The basic idea is to project system (1.1) to Ker(DT) for getting a system with a homogeneous boundary condition.We first show the idea by a simple example,and present the general procedure later. Example 1Consider the following system First let We have Then,applying the row-vectors (1,0,0) and (0,1,0) in Ker(DT) to system (1.3),we get The reduced system (1.4) is for the variablesu1andu2,so at the first step,the variableh(1)=−u3can be formally regarded as an internal control appearing in system(1.4).However,the value ofh(1)can not be freely chosen,then we call it as an indirect internal control. Next let We have Then,applying the row-vector (1,0) in Ker(DT1) to the reduced system (1.4),at the second step we get This is a system for the variableu1,in which the variableh(2)=−u2can be regarded as an indirect internal control. Finally,let Since Ker(DT2)=(0),we stop the projection. By this way,we decompose the original system (1.3) into two sub-systems (1.4) and (1.5).Consequently,besides the direct boundary controlhacting on the boundary and appearing in the original system (1.3),we find two indirect internal controlsh(1)andh(2),which are hidden in the sub-systems (1.4) and (1.5),respectively. Related to the indirect controllability,the notion of the indirect stabilization was introduced by Russell[16]in the early 1990’s.It concerns if the dissipation induced by one of the equations can be sufficiently transmitted to the other ones in order to realize the stability of the overall system(see[2–3]for wave equations and[14–15]for wave/heat equations).Moreover,as shown in [4,13],the situation is more complicated for partially damped systems.The effectiveness of the indirect damping depends in a very complex way on all of the involved factors such as the nature of the coupling,the order of boundary dissipation,the hidden regularity,the accordance of boundary conditions and many others. The paper is organized as follows.In§2,we will give a general procedure of projection,which decomposes a system of wave equations into a sequence of sub-systems.In §3,we establish the relation between the ranks of the matrices appearing in the procedure of projection.In §4,we identify the indirect internal controls in the reduced systems and explain its role in the systems.In §5,we establish a uniqueness theorem under Kalman’s rank condition without any algebraic condition on the coupling matrix,neither any geometrical condition on the controlled domain.This result will be served as a base for the approximate controllability by locally distributed controls later.§6 is devoted to some questions to be developed in the forthcoming work. Now we describe the general procedure of projection.Let whereA0is a matrix of orderN0,D0is a matrix of orderN0×Mwith D0is not necessarily a full column-rank matrix. Let We choose In particular,we have Noting there exist a matrixA1of orderN1and a matrixD1of orderN1×M,such that SinceK0is of full column-rank,A1is uniquely determined.While,sinceD0may be not of full column-rank,for guaranteeing the uniqueness ofD1,we require Then,noting (2.3),by applyingKT0to system (1.1) and setting we get The projected system (2.8) is not self-closed in general.It can be regarded as a system for the reduced variableU(1),associated with the internal controlH(1). Similarly,by the successive projections,forl=2,3,···,we get Forl=1,2,···,let Define In particular,we have Noting that there exist a matrixAlof orderNland a matrixDlof orderNl×M,such that Then,noting (2.12),we have and SinceKl−1is of full column-rank,we have Ker(Kl−1)={0}.It follows from (2.15) that While,sinceDl−1may be not of full column-rank,Ker(Dl−1)≠{0} in general.In order to uniquely determine the matrixDlby the relation (2.16),similarly to (2.6),we require Then,applyingKTl−1to system (2.9) and setting we get We continue the procedure of projection until (i) eitherDL=0,then we get a self-closed conservative system which is not approximately controllable,so is the original system (1.1); (ii) or Ker(DTL)={0},then we get a non self-closed system Since the control matrixDLis of full row-rank,this case is favorite for the approximate controllability of system (2.22),however,we don’t know whether the original system (1.1) is actually approximately controllable or not. The above procedure is purely algebraic.In order to clarify the leading idea,we do not take other type boundary conditions into account. Let us recall the following fundamental result (see [7,Lemma 2.5]). Lemma 3.1Let d≥0be an integer.The rank condition holds if and only if d is the largest dimension of the subspaces,which are contained inKer(DT)and invariant for AT. Proposition 3.1Let l be an integer with1≤l≤L.For any subspace V contained inKer(DTl)and invariant for ATl,there exists a subspace W contained inKer(DTl−1)and invariant for ATl−1,such thatdim(W)=dim(V),and vice versa. ProofFirst,letV⊆Ker(DTl) be an invariant subspace ofATl.LetW=Kl−1(V) denote the direct image ofVbyKl−1. For any giveny∈W,by the definition ofW,there existsx∈V,such thaty=Kl−1x.ApplyingxTto (2.14) leads that Sincex∈V⊆Ker(DTl),we havexTDlDTl−1=0,then Moreover,sinceVis invariant forATl,we haveATlx∈V,then it follows from (3.2) that By (2.12),we have ThusWis contained in Ker(DTl−1) and invariant forATl−1. Inversely,letW⊆Ker(DTl−1) be an invariant subspace ofATl−1.Let denote the inverse image ofWbyKl−1.For any givenx∈V,there existsy∈W,such thatKl−1x=y.ApplyingxTto (2.14),we get ApplyingKl−1from the right to the above relation,it follows that By (2.12),DTl−1Kl−1=0,then SinceWis invariant forATl−1,we haveATl−1y∈W.By the definition ofV,there existsx∈V,such thatKl−1x=ATl−1y.Then,it follows from (3.4) that SinceKTl−1Kl−1is invertible,we have namely,Vis invariant forATl. Finally,insertingKl−1x=yandATlx=xinto (3.3),and notingKl−1x=ATl−1y,we get ThenDl−1DTlx=0.By (2.18),we getDTlx=0. So,V⊆Ker(DTl).Moreover,sinceKl−1is of full column-rank,we have dim(V)=dim(W). Proposition 3.2We have ProofWe first show that for 1≤l≤L,we have In fact,let By Lemma 3.1,pl−1is the dimension of the largest subspace which is contained in Ker(DTl−1)and invariant forATl−1.By Proposition 3.1,the largest subspace which is contained in Ker(DTl)and invariant forATlhas also the dimensionpl−1.Then we have Noting (2.10) and combining (3.7)–(3.8),we get (3.6). Then,the summation of (3.6) forlfrom 1 toLgives At theL-th step of reduction,we have eitherDL=0,then or Ker(DTL)=0,then Then,using (3.10) and (3.11) in (3.9),we get (3.5). Proposition 3.3rank(Dl,AlDl,···,Dl)−Nlis a constant with respect to l with0≤l≤L.Consequently,Kaman’s rank condition holds for all l with0≤l≤L if and only ifKer(DTL)={0}. ProofFirst,using (2.10) and (3.6),we deduce Next,assume that condition (3.12) holds for alllwith 1≤l≤L.In particular,we have SinceNL>0,we haveDL≠0.By the alternative of reduction,we get Ker(DTL)={0}. Inversely,by Lemma 3.1,condition Ker(DTL)={0}implies condition(3.14).Then,it follows from relation (3.13) that condition (3.12) holds for alllwith 1≤l≤L. Proposition 3.4Let A be a cascade matrix andΩsatisfy the geometrical control condition.Then system(1.1)is approximately controllable if and only ifKer(DTL)={0}. ProofBy[7](see also[1]),system(1.1)is approximately controllable if and only if the pair(A,D) satisfies Kalman rank condition (1.2),or equivalently,by Proposition 3.3,if and only if Ker(DTL)={0}. At the end of the section,we give two others examples for further illustrating the reduction procedure. Example 2Consider the following system Let Noting (2.1)–(2.2),we may take Then,using (2.16)–(2.17) withl=1,a straightforward computation gives and ApplyingKT0to system (3.15),we get where and This is a system for the variablesu1,v1andη1.The variableh1can be regarded as an internal control in system (3.16). Next,applying (2.16)–(2.17) withl=2 to we get ApplyingKT1to system (3.16),we get where SinceD2=0,we stop the projection withN2=2.By Proposition 3.3,none of the pairs(A0,D0),(A1,D1)or(A2,D2)satisfies Kalman’s rank condition(3.12).More precisely,we have rank(D0,A0D0,A20D0,A30D0)−4=rank(D1,A1D1,A21D1)−3=rank(D2,A2D2)−2.Noting rank(D2,A2D2)=0,it follows that rank(D0,A0D0,A20D0,A30D0)=4−2=2,rank(D1,A1D1,A21D1)=3−2=1. Example 3Consider the following system. Let Noting (2.1)–(2.2),we may take Using (2.16)–(2.17) withl=1,a straightforward computation gives and Then,applyingKT0to system (3.18),we get where This is a system for the variablesv1,v2with an internal controlh1. Next,applying (2.16)–(2.17) withl=2 to we get Then,applyingKT1to system (3.18),we get where This is a system for the variablev2with an internal controlh2.Since Ker(DT2)={0},we stop the projection. Since Ker(DT2)={0},we stop the projection withN2=2.By Proposition 3.3,the pairs(A0,D0),(A1,D1) and (A2,D2) satisfy Kalman’s rank condition (3.12). For 1≤l≤L,the termH(l)can be formally regarded as internal controls in the sub-system(2.20).But the value ofH(l)is given by (2.19),therefore,it can not be freely chosen.So,H(l)(1≤l≤L) will be called indirect internal controls,and accordingly,rank(Dl) denotes its number.Thus,the original system (1.1) is directly controlled by the boundary controlH(0),and indirectly controlled by the internal controlsH(1),···,H(L)which are hidden in the subsystem (2.20) and intervene into the systems at different steps of the reduction.Moreover,the formula (3.5) justifies well the notion of the total number of (direct and indirect) controls previously introduced in [8].This gives a pretty good explanation to the indirect controls. The term “direct controls” or “indirect controls” is related to the sub-system (2.20).For 1≤l≤L,H(l)can be regarded as direct internal controls in (2.20) at thel-th step or as indirect controls for the original system(1.1).In any case,this is simply a terminology that we can use as we want. Proposition 4.1Assume that system(1.1)is approximately controllable.Then for all l with1≤l≤L,the rank condition(3.12)holds and the sub-system(2.20)is approximately controllable by the internal indirect control H(l). ProofFirst by Proposition 3.3 and noting (1.2),we have On the other hand,by (2.19),we have Then,the approximate controllability of system (1.1) implies that of the sub-system (2.20) for alllwith 1≤l≤L. We know few about the structure of indirect controlsH(l)with 1≤l≤L,however,the following result shows that the indirect controlsH(l)should be so smooth that its action on the sub-system (2.20) will be very weak,especially as the steplincreases. Proposition 4.2For any given l with1≤l≤L,let Then,we have ProofFor any givenand any givenH∈(L2loc(R+;L2(Γ)))M,the solution to problem (1.1)–(1.2) has the regularity (see [7–8,10]): Forl=1,consider the reduced system with the initial data: Since the right-hand side the solution to problem (4.3)–(4.4) has the regularity (see [11]or [12]) The general case can be easily completed by a bootstrap argument. This section gives only a brief abstract on the internal controllability.It will be carefully completed in a forthcoming work. Now we consider the system for the variableU=(u(1),···,u(N))T: with the initial data whereH∈(L2loc(R+;L2(Ω)))Mandχωis the characteristic function of a subsetωof Ω. Remark 5.1The global caseω=Ω is trivial,so less interesting.For the exact controllability,ωis often assumed to be a neighbour of Γ in the literature,while for the approximate controllability,it seems that no restriction onωwill be necessary. Definition 5.1System(5.1)is approximately controllable at the time T >0if for anygiven initial data∈(L2(Ω) ×H−1(Ω))N,there exists a sequence{Hn}of controlsin(L2loc(R+;L2(Ω)))Mwith support in[0,T],such that the corresponding sequence{Un}of solutions satisfies Similarly to the approximate boundary controllability in [9],we can show the equivalence between the approximate controllability of system (5.1) and the uniqueness of solution to the following adjoint system for the variable Φ=(φ(1),···,φ(N))T: associated with the internal observation Moreover,condition (1.2)is still necessary for the uniqueness of solution to the overdetermined system (5.4)–(5.5). Theorem 5.1If A satisfies Kalman’s rank condition(1.2),then system(5.4)–(5.5)has only the trivial solution.Consequently,system(5.1)is approximately controllable by locally distributed controls. ProofTo be clear,let Φ ∈(C0(R;H10(Ω)) ∩C1(R;L2(Ω)))Nbe a solution to system(5.4)–(5.5).First,applyingDTto the equations in (5.4) and noting (5.5),we get Then,successively applyingDTAT,DT(A2)T···to the equations in (5.4),we get therefore, By (1.2),the matrix (D,AD,···,AN−1D) is of full row-rank,then Thus,applying Holmgren’s uniqueness theorem,we get Φ≡0 in (0,T)×Ω,provided that whered(Ω) denotes the geodesic diameter of Ω (see [10,Theorem 8.2]). Remark 5.2Since the differential operator ∆commutes with the internalD-observation(5.5): the situation is almost the same as for ordinary differential equations (see [5]).This is why the uniqueness in Theorem 5.1 holds without any restriction on the coupling matrixA,nor on the damped sub-domainω. Remark 5.3Recall that the controllability time (optimal) for system (1.1) is given by It should be sufficiently large,especially asNis large(see [7,17]).However,the controllability time given by (5.10) is independent of the number of equations and of the number of applied controls.It is exactly the same as for a sole equation in [10]. After having discussed the notion of indirect controls,further work would be needed to develop new results.For example,some interesting problems could be considered as follows. Question 1Since the value ofH(l)can not be freely chosen,the indirect internal controlsH(l)in the sub-system (2.20) has not the same meaning as the direct internal controlsHin(5.1).Any initiative for further clarifying their relations would be interesting to pursue. Question 2The adaptation of the procedure to the coupled system of wave equations with coupled Robin controls (with two coupling matrices) might be an interesting direction to be investigated. AcknowledgementThe authors would like to thank the reviewer’s valuable comments.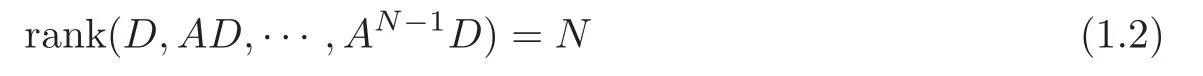

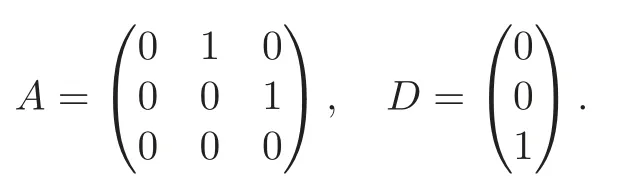

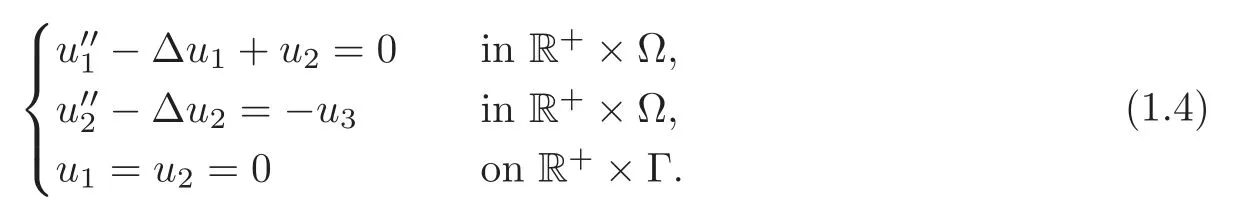




2 An Algebraic Procedure of Reduction

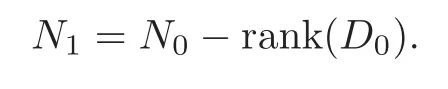
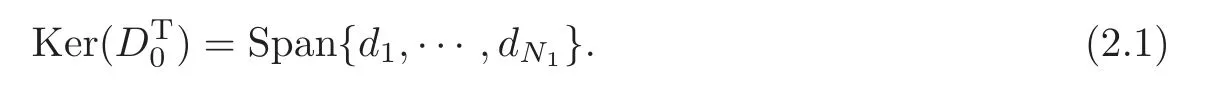





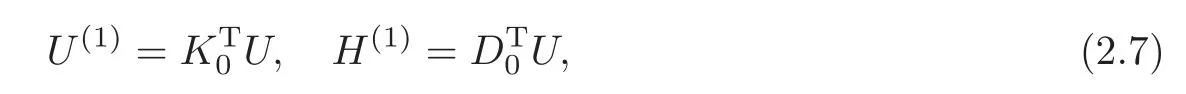

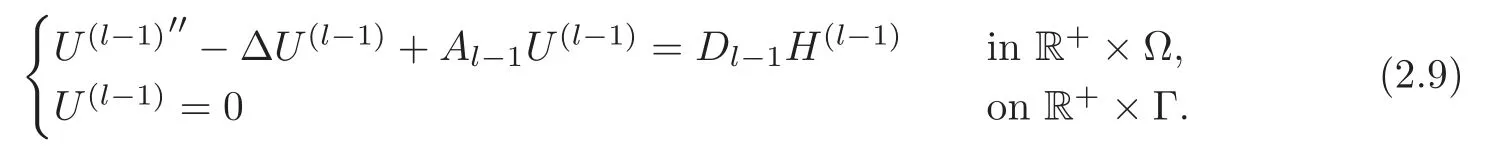





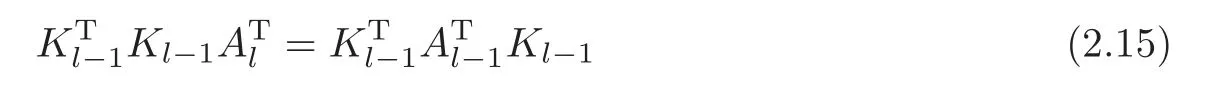

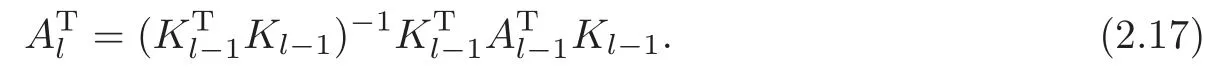

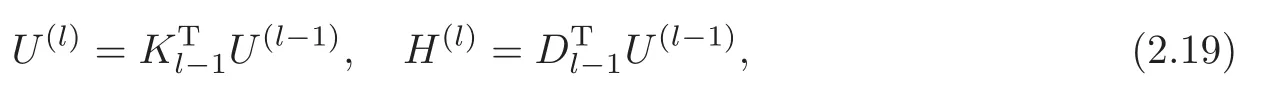

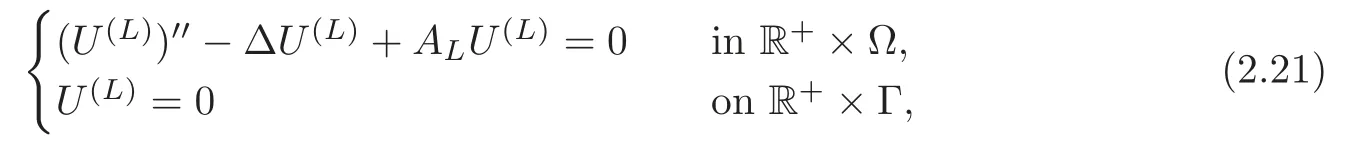

3 Mathematical Analysis
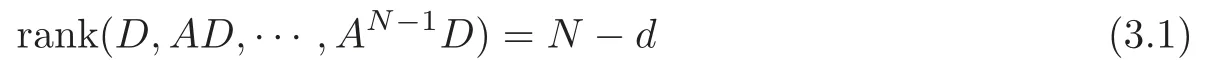







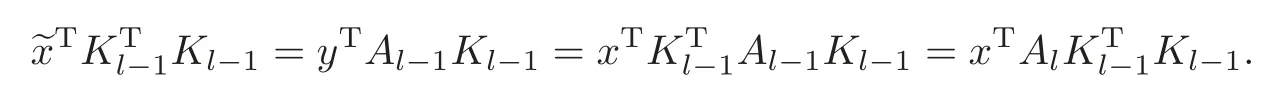
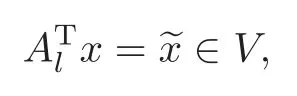

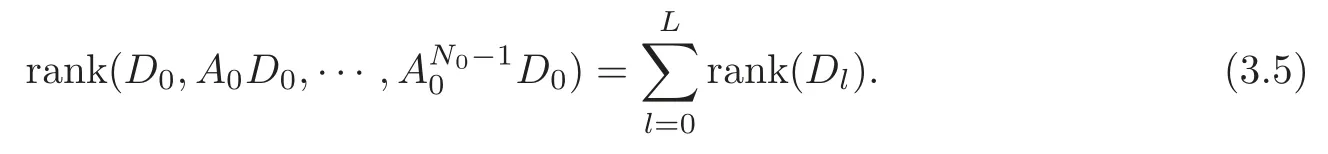
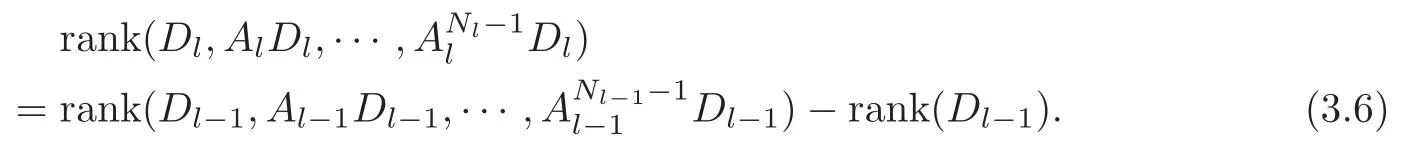
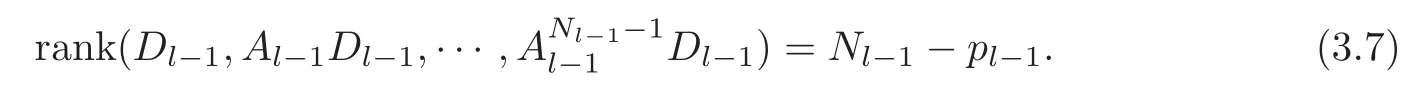

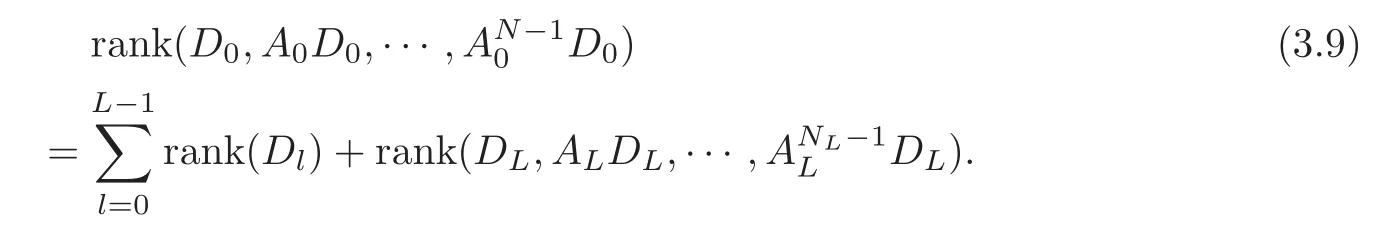
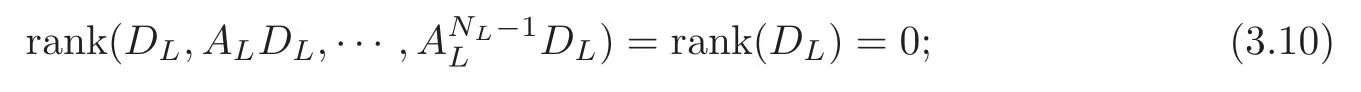
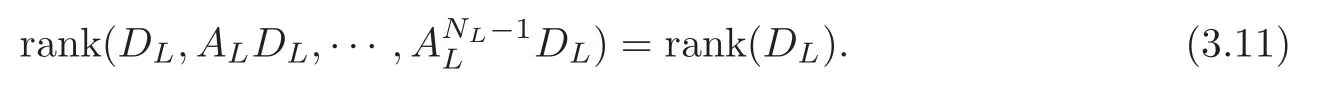

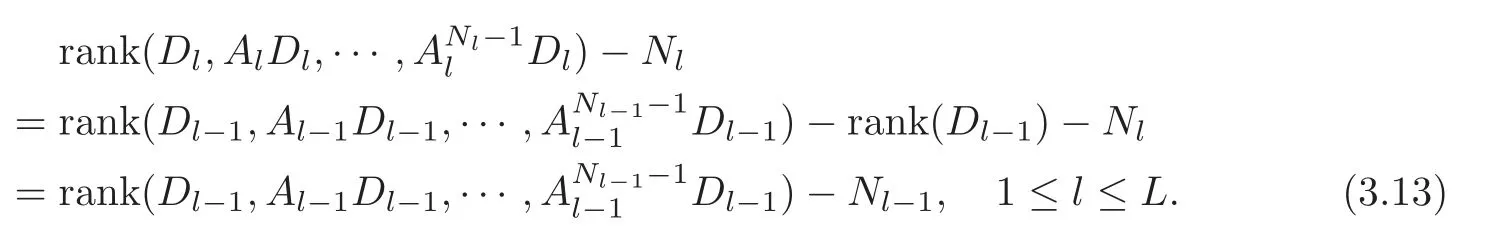
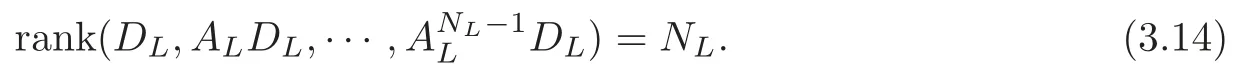

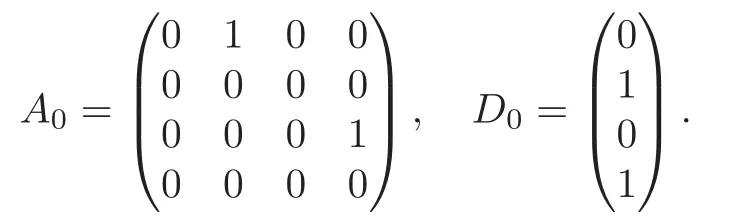
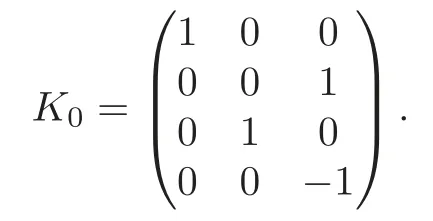
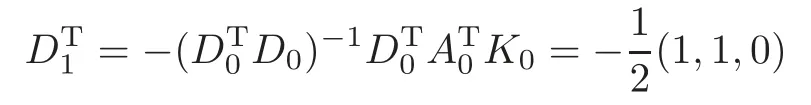
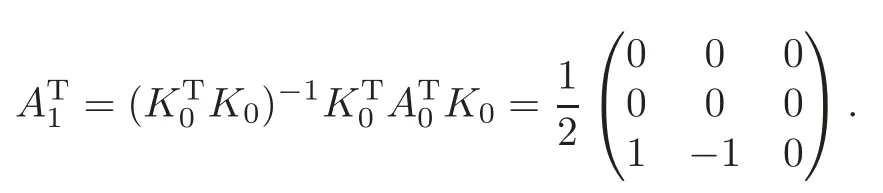


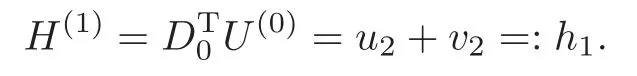
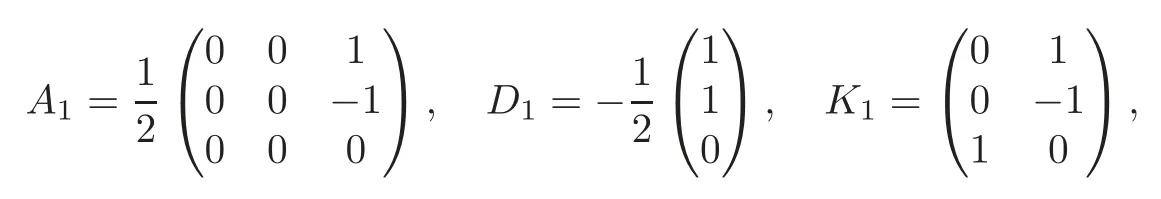

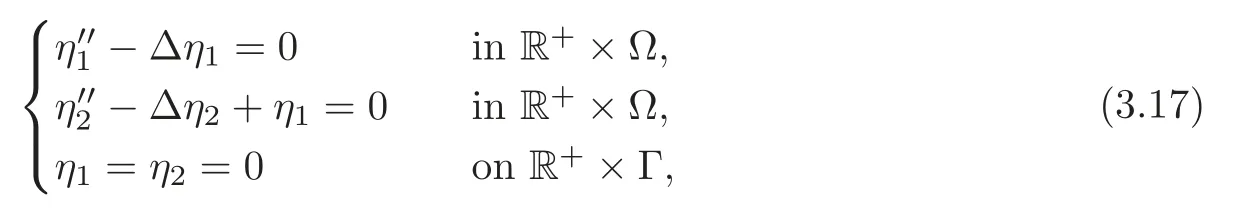
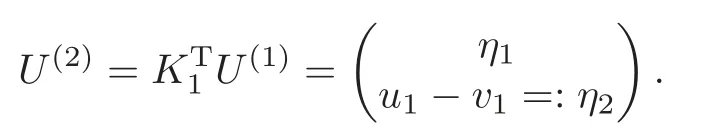

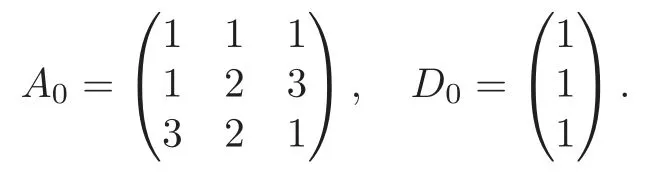
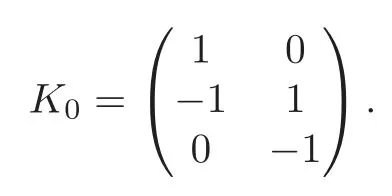


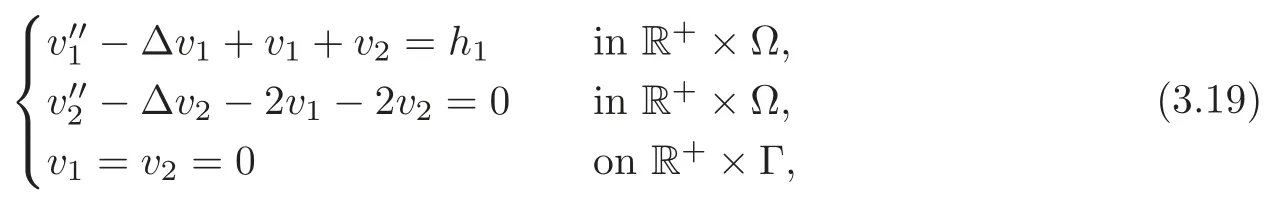

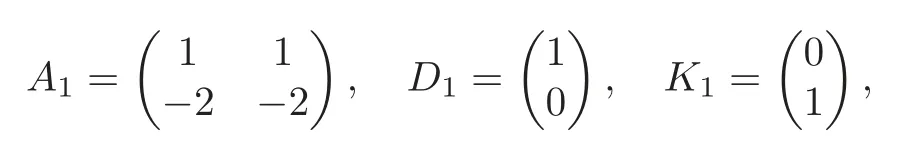


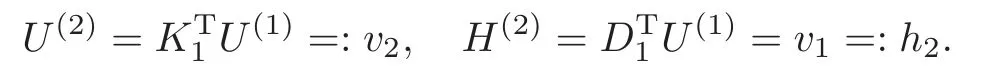
4 Notion of Indirect Controls
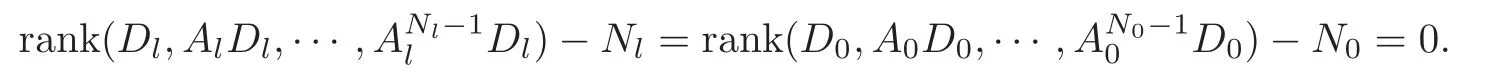



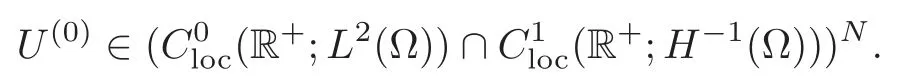
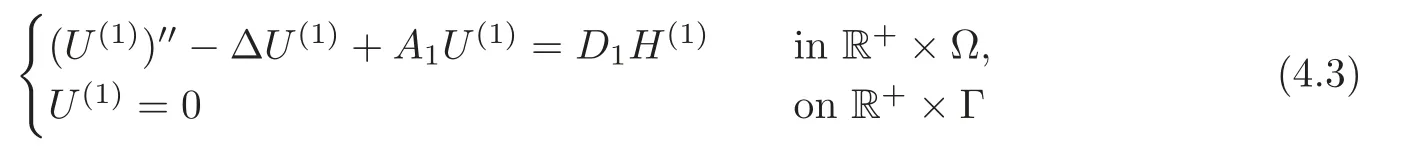

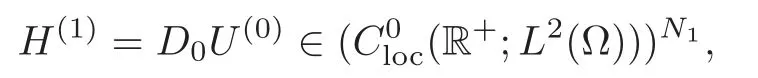

5 Approximate Controllability by Locally Distributed Controls
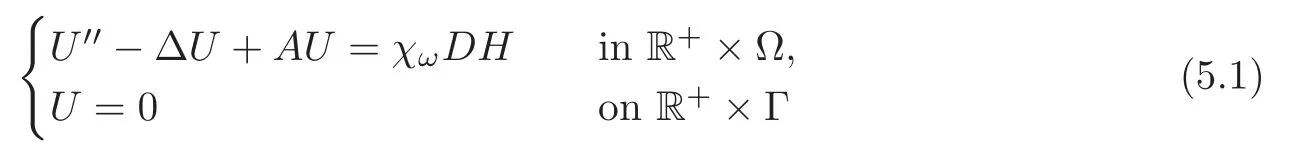
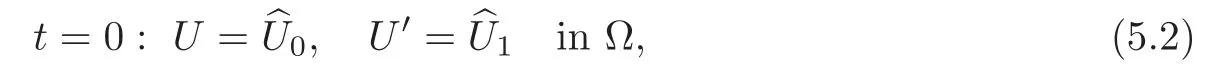
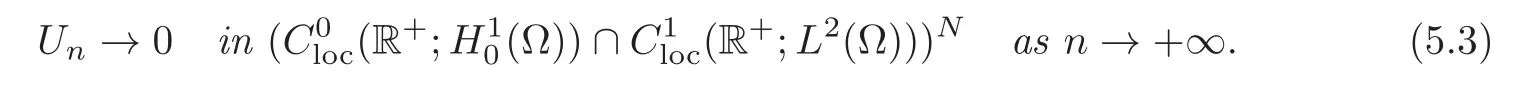



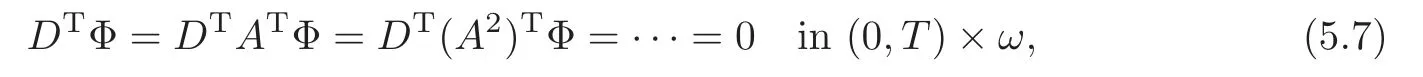





6 Comments
杂志排行
Chinese Annals of Mathematics,Series B的其它文章
- Ground States of K-component Coupled Nonlinear Schrödinger Equations with Inverse-square Potential∗
- Rotational Hypersurfaces with Constant Gauss-Kronecker Curvature
- A Generalization of Lappan’s Theorem to Higher Dimensional Complex Projective Space∗
- Cartan’s Second Main Theorem and Mason’s Theorem for Jackson Difference Operator∗
- Products of Toeplitz and Hankel Operators on Fock-Sobolev Spaces∗
- On a Supercongruence Conjecture of Z.-W.Sun∗
