基于指条厚度优化的冷凝式声表面波气体传感器灵敏度提升方法

邹亮桃 刘久玲 游 然 刘明华 任 伟 何世堂

(1 中国科学院声学研究所 北京 100190)

(2 中国科学院大学 北京 100049)

0 引言

声表面波(Surface acoustic wave,SAW)气体传感器因其灵敏度高、几何尺寸小、易于集成及大规模生产等优点[1]，在环境保护、公共安全以及国防科技等多个领域具有广阔的应用前景。由于SAW检测器本身对待测气体没有选择性，只能够确定检测量的大小，而不能分辨检测物的成分，需要与化学手段结合才能实现定性。因此，典型的SAW气体传感器常采用在器件表面涂覆选择性敏感膜的方法来检测待测气体，但该方案受限于敏感膜限制了气体检测的种类，并且存在交叉干扰问题[2]。20世纪末，研究人员提出将SAW 技术与传统的气相色谱(Gas chromatograph,GC)联用[3]，首先通过气相色谱分离气体实现定性分析，继而将不同时间上分离出来的气体附着于SAW 器件表面实现定量分析，从而克服了典型SAW 气体传感器的缺点，成功实现复杂环境下的气体分析。因此，GC/SAW 系统的相关研究受到广泛关注[2−7]。

在此基础之上，为了使GC/SAW 联用技术更好地满足实际应用的需求，研究人员进一步对影响其灵敏度的因素进行了研究，包括谐振器的谐振腔长度[8]、谐振器的负载区域位置[9]以及退火温度[10]等，进一步提升了GC/SAW 系统的性能。然而，在指条厚度对SAW 检测器灵敏度的影响方面，相关研究较少。2019年，郝文昌等[11]研究了负载为固体时，谐振器指条厚度对灵敏度的影响。然而，当负载为液态时，指条厚度对SAW 检测器灵敏度的影响分析的研究却较少。考虑到液体层只能耦合声纵波，而固体层却能耦合纵波和剪切波，因此，当固体中的声波传播到液体中时的边界条件和声波在两种固体之间传播时差别较大，所以对液膜负载的模拟是很有必要的。因此，本文基于流固耦合理论与压电效应相结合理论，探究了液态负载下谐振器指条厚度对灵敏度的影响。

本文采用有限元商业软件建立流体负载与压电效应相耦合的三维有限元模型，并结合SAW 的耦合模(Coupling-of-modes,COM)理论实现对器件的快速准确模拟。从理论和实验两方面研究了负载为液膜时，谐振器指条厚度对冷凝式SAW 气体传感器灵敏度的影响，为GC/SAW 系统检测性能的提升提供新思路。

1 理论分析

GC/SAW 系统的原理是首先利用GC 柱出口温度与SAW 检测器表面温度之间的温度差，使待测气体从GC 柱口出来遇冷快速凝结吸附在SAW检测器表面，从而在器件表面形成了一层薄液膜；然后再利用液膜负载引起的器件表面边界条件的改变，进而引起检测器频率的变化，如图1所示[12]。在检测过程中待测气体冷凝形成液膜覆盖在器件表面时，液膜直接接触的边界分为两种：一种与金属指条直接接触；一种与压电基底直接接触。压电基底上表面的边界条件是由液膜与压电基底和金属指条与压电基底两种情况交叉形成的，如图2所示。同时，声波在不同物质中的波动方程也是不一样的。液体层只能耦合声纵波，而固体层却能耦合纵波和剪切波，因此，固体中的声波传播到液体中和声波在两种固体之间传播的边界条件不同造成了声波的传播方式的改变。

图1 吸附原理Fig.1 Adsorption principle

图2 有液膜负载的结构图Fig.2 Structure diagram with liquid membrane load

首先对压电晶体中的声场进行分析，需要同时考虑力学作用和电学作用。在压电晶体中，不存在彻体力，一般是绝缘体，不存在自由电荷。此时，压电晶体内的耦合波动方程为[13]

式(1)中，u、Φ、ρ分别为位移、电势、密度，cE、e、εS分别为晶体的弹性劲度常数、压电应力常数、介电常数，i,j,k,l=1,2,3。

当边界条件是由金属指条与压电基底构成时，金属指条或各向同性固体中的波动方程为

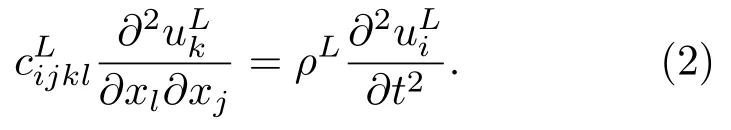
当边界条件是由液膜与压电基底构成时，液膜中的波动方程需要考虑黏滞作用。根据纳维-斯托克斯(N-S)方程，当液体的黏滞系数µ为常数时，液膜中的波动方程为[7,14]

式(2)中，ul、ρl分别表示位移和液体密度，clijkl为弹性劲度常数，∇·ul是位移的散度，µ为黏滞系数。

其中，任何结构下介质中声波的准确求解都需要从波动方程出发，得到Christoffel 方程来求解得到满足特定边界条件的声波解。由上述3 个式子可以看出，不同性质负载(固体、液体)的波动方程不同，引起的边界条件也会有所差别。

为了分析复杂的不连续边界结构，本文将利用耦合模理论结合多物理场耦合的有限元方法对液膜负载下的器件响应开展仿真研究。

1.1 COM理论

COM 模型为模拟和仿真不同结构的SAW 器件提供了有效的方法。忽略栅阵中传播损耗的影响，COM方程可写为[15]

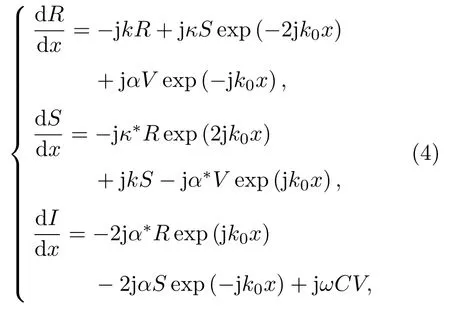
其中，R和S分别表示右向、左向传播的平面波，V表示交变电压，I表示交变电流，k是SAW 的波数，k0是声同步波数，κ表示耦合系数，α表示激发系数，C是单位长度的静态电容。

当V=0 时，叉指换能器(Interdigital transducer,IDT)的电端短路，此时栅阵中无激发源，即相当于周期短路栅阵；当I=0 时，IDT 的电端开路，此时栅阵中不存在电流，即相当于周期开路栅阵。根据文献[9]可知，通过周期短路栅阵和周期开路栅阵的禁带边界频率可以直接推导出COM 参量(中心频率f0(或传播速度v)、耦合系数κ、激发系数α和静态电容C)的解析表达式：

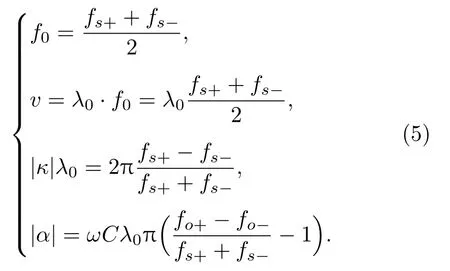
当在Al 电极上施加交变电压∆V时，归一化静态电容Cn为

其中，W为声孔径。

1.2 有限元方法提取耦合模参量

COM 理论是一种近似的唯象模型，所用参量的数值必须由精确理论或实验来确定，参量的准确度决定了分析SAW 器件的精确程度。因此为保证COM 参量提取的准确性和便捷性，本文对器件进行三维有限元分析，使用多物理场商业仿真软件建立液膜负载下，流体声学与压电物理场的耦合物理模型，提取特征频率，获得周期短路栅阵和周期开路栅阵的禁带边界频率，进而对参量进行提取。

首先，在有限元商业软件中建立SAW 三维有液膜负载的周期模型时，需要考虑液膜负载导致的压电基底表面边界条件的不连续性。因此，应基于流固耦合与压电效应相结合建立有液膜负载的三维周期模型，如图3所示。其中，灰色区域为压电基片，白色区域为理想导体的铝指条，同时，考虑到实际的冷凝结果，沿x方向(XY平面)均保持一致高度的表面深灰色区域为液膜负载。

图3 有液膜负载的三维周期模型Fig.3 Three-dimensional periodic model with liquid membrane load

其次关于边界条件。液膜与压电基片和指条的连接界面上，由于介质属性不同(负载为流体、器件为固体)，存在流固边界，需额外考虑流固耦合作用。因此，与无液膜负载的周期模型[11]相比，除了需要ST-X 石英压电基片与铝电极之间固体力学与静电之间的压电耦合接口，还需要增加液膜与压电基片和指条之间固体力学与压力声学之间的流固耦合接口，此接口对应的流固边界条件为

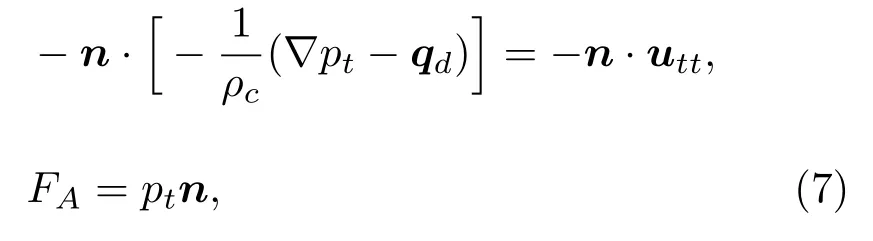
其中，utt是结构加速度，n是表面法线，pt是总声压，FA是结构承受的载荷(每单位面积的力)。

其他具体的力学、电学以及压力声学的边界条件列于表1。

表1 模型的边界条件Table 1 Boundary conditions of the model

然后，采用立方体单元对图3中的模型进行网格划分。由于SAW主要在表面附近传播，位移最大，且IDT 是设计SAW 器件的关键，为了使模拟结果更精确，IDT 和表面附近的网格密度更大。IDT 结构的变形，使得液膜流场的计算域发生变化，要考虑流场网格随声波变形以适应耦合界面的变形，还需要考虑动网格中变形域的问题，因此液膜采用自由四面体网格进行划分。网格划分如图4所示。

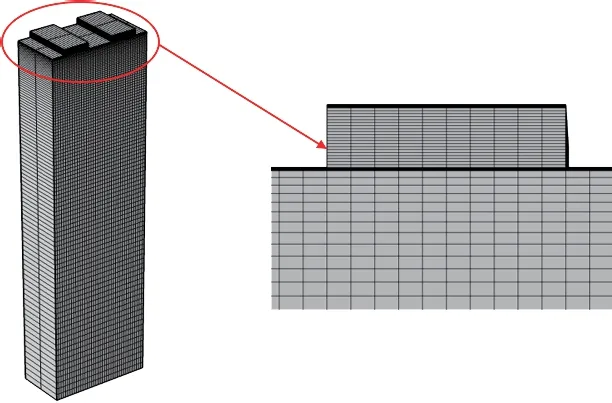
图4 模型的网格划分Fig.4 Model meshing

接着，通过模态分析，仿真获得周期短路和开路栅阵的禁带边界频率，即对称模式和反对称模式。其中，将电极的电学边界条件Γ+设置为电压Vt=1，Γ−设置为接地，获得周期短路栅阵的禁带上下边界频率(fs−，fs+)；同理，将电极的电学边界条件Γ+设置为电荷Q=0，Γ−设置为接地，获得周期开路栅阵的禁带上下边界频率(fo−，fo+)。液膜负载采用厚度为5 nm的甲基膦酸二甲酯(DMMP)，其无液膜负载和有液膜负载时的禁带边界频率如图5(a)和图5(b)所示。利用前面推导的求解COM参量的公式，提取出周期结构的COM 参量(传播速度ν、耦合系数κ、激发系数α)。

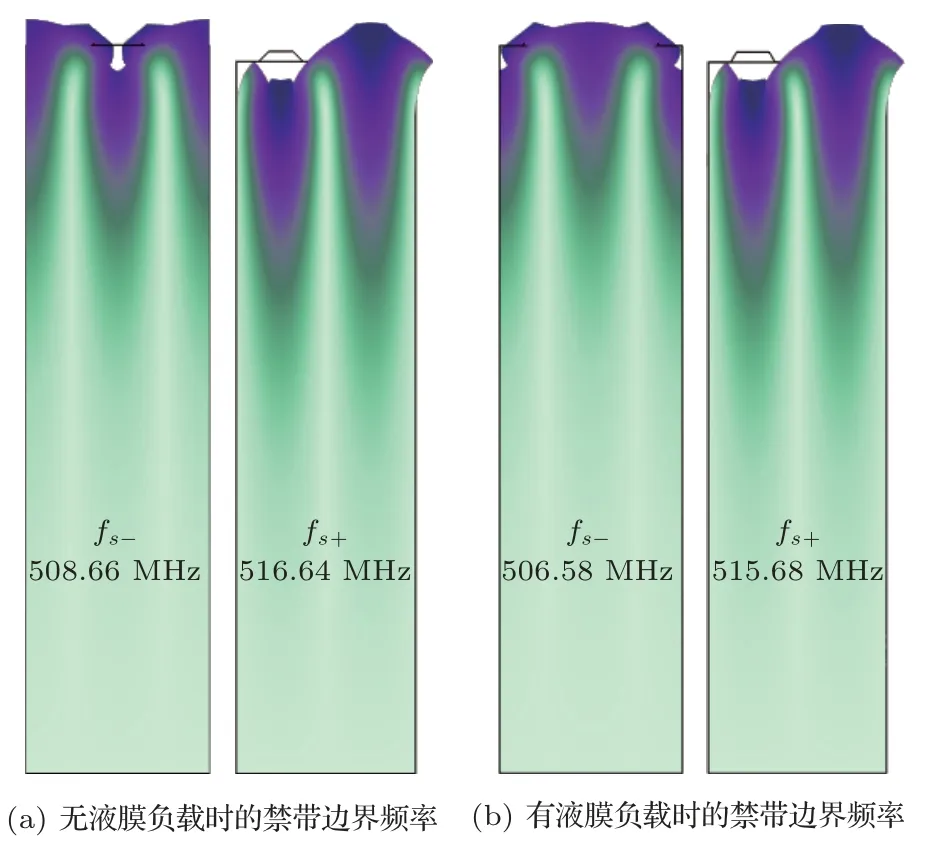
图5 液膜负载前后SAW 谐振器的禁带边界频率Fig.5 Band gap boundary frequencies of SAW resonators before and after liquid film loading

最后，通过静态分析得到静态电容C[11]：

又

当Al 电极上施加交变电压Vt时，归一化静态电容Cn为

与有液膜负载的周期结构类似，通过有限元方法分别对有液膜负载和无液膜负载的周期结构进行建模，模态分析得到禁带边界频率，结合COM理论，提取出无液膜负载和有液膜负载周期结构的COM参量。

1.3 1-3模式下的PPP 矩阵模型

本文对三换能器的双端对谐振器结构进行理论和实验分析，它由3 个换能器和两侧相同的金属短路栅阵构成，其结构如图6所示。

图6 三换能器双端对SAW 谐振器的结构示意图Fig.6 Schematic diagram of the three-transducer dual-end pair SAW resonator

为了得到1-3 模式结构双端对SAW 谐振器的频率响应，可以将其划分为若干个周期性或准周期性结构，而每一部分均可用P矩阵来表示，如图7所示。

图7 1-3 模式谐振器的P 矩阵模型Fig.7 The P matrix model of 1-3 mode resonator

P矩阵元为

其中，结构参量L为IDT 长度，N为电极对数，即L=Nλ0，Re 为取实部运算。由式(11)P矩阵元的计算公式可知，其由COM 参量和结构参量决定。利用有限元方法结合COM 理论提取出负载前后的COM 参量代入每一部分的P矩阵，用P矩阵级联技术得到SAW 检测器导纳矩阵Y，通过网络参量转换关系得到检测器频率响应。转换关系如式(12)所示：

2 数值结果

图6所示的1-3模式SAW谐振器的结构参数如表2所示。图3所示的仿真模型中采用的压电、电极材料分别是ST-X 石英压电基片和铝电极，参数分别如表3、表4所示，液膜负载采用厚度为5 nm 的DMMP、烷烃(C7、C8)，材料参数如表5。

表2 SAW 谐振器结构参数Table 2 SAW resonator structure parameters

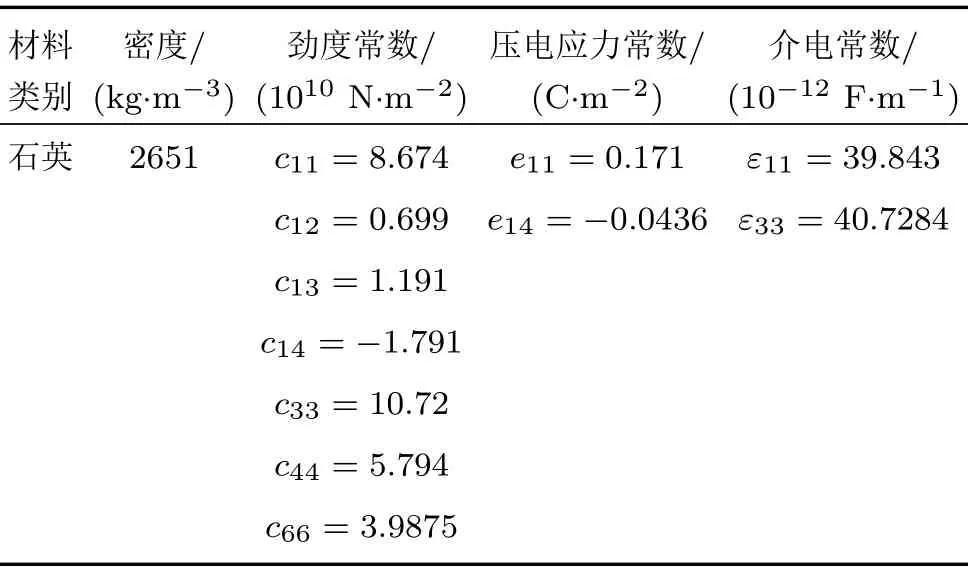
表3 压电石英基片的材料参数Table 3 Material parameters of piezoelectric quartz substrate

表4 铝电极的材料参数Table 4 Material parameters of aluminum electrode

表5 DMMP 和烷烃(C7、C8)的材料参数Table 5 Material parameters of DMMP and alkanes (C7,C8)

本文采用的IDT 波长λ=6 µm，电极宽度a=λ/4，电极厚度h ∈[0,550 nm]。基于上述理论以及参数，通过有限元商业软件建立仿真，结合COM理论提取液膜负载前后的COM 参量，代入P矩阵，利用P矩阵级联技术计算得到液膜负载前后中心频率变化量。以指条厚度h=300 nm、负载为DMMP的周期结构为例，提取液膜负载前后检测器的归一化COM 参量如表6所示，频率响应如图8所示，实线和虚线分别表示无液膜负载和有液膜负载时的频率响应，两个中心频率的差值即为液膜负载引起的频率偏移。

图8 液膜负载前后SAW 谐振器的频率响应(h=300 nm)Fig.8 Frequency response of SAW resonator before and after liquid membrane loading (h=300 nm)

表6 DMMP 负载前后周期结构的COM 参量Table 6 COM parameters of periodic structure before and after DMMP load

经进一步计算发现，对大多数液体负载而言，当液体的黏滞系数很低时，其黏滞系数和声波波速不同对灵敏度的影响很小，可以忽略不记。本节将选用DMMP 和正庚烷(C7)作为模拟液膜负载，经计算可得指条厚度在h ∈[0,550 nm]区间内，DMMP、C7 液膜负载前后的中心频率变化量，如图9、图10所示。结果表明，当DMMP 冷凝为液膜作为模拟负载时，SAW检测器的灵敏度随着电极厚度的增加先变大后减小；当C7 冷凝为液膜作为模拟负载时，SAW检测器的灵敏度随着电极厚度的增加先增加后减小，再有小幅度的上升，最优归一化电极厚度为6.4%～7.6%之间。

图9 DMMP 液膜引起的中心频率偏移量随电极厚度变化理论图Fig.9 Theoretical diagram of the center frequency shift caused by the DMMP with the electrode thickness

图10 C7 液膜引起的中心频率偏移量随电极厚度变化理论图Fig.10 Theoretical diagram of the center frequency shift caused by the C7 with the electrode thickness

3 实验部分

为验证上述理论分析，本次实验在ST-X 石英压电表面沉积了6 种电极厚度(徕卡DCM8 显微镜干涉测量模式实测值)：253.7 nm、297.7 nm、366.2 nm、389.5 nm、461.9 nm、508.9 nm，制备相应的SAW 器件进行了实验。图11为完好的SAW器件。

图11 SAW 实验器件Fig.11 SAW experimental device

3.1 实验条件

色谱柱的初始温度45◦C，升温至180◦C，柱流量3 mL/min；进样口温度200◦C；六通阀温度165◦C；检测器温度40◦C；氦气作载气；泵吸时间40 s，实验装置如图12所示。

图12 实验平台Fig.12 Experimental platform

实验样品：质量浓度为0.0016 mg/mL 的DMMP溶液；体积浓度为3×10−6浓度的C7；体积浓度为1.5×10−6浓度的C8。

3.2 结果与讨论

为了避免特殊性，减少单次测量的误差，采用每个器件测6 组数据、多次实验结果取平均值的方法。上述6 种电极厚度的SAW 检测器在本课题组自行研制的GC/SAW 系统中进行DMMP、C7、C8响应实验，实验结果如图13、图14、图15所示。从图中可以看出，当DMMP 为实验样品时，灵敏度随电极厚度变化趋势是先升高后下降，最优电极厚度在6.4%～7.6%之间；当C7、C8 为实验样品时，灵敏度随电极厚度变化趋势是先升高后下降，再小幅度的升高，最优电极厚度在6.4%～7.6%之间。从中可以看出实验和理论中器件灵敏度随叉指厚度的变化趋势吻合良好，这也验证了前面的理论分析。

图13 0.0016 mg/mL DMMP 引起的响应值随电极厚度变化实验图Fig.13 The experimental graph of the response caused by 0.0016 mg/mL of DMMP with electrode thickness

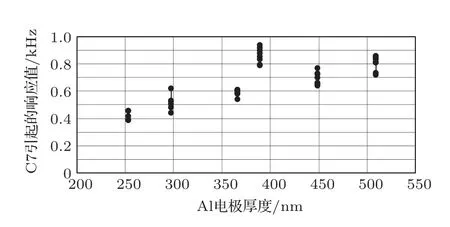
图14 3×10−6 C7 引起的响应值随电极厚度变化实验图Fig.14 The experimental graph of the response caused by 3×10−6 of C7 with electrode thickness

图15 1.5×10−6 C8 引起的响应值随电极厚度变化实验图Fig.15 The experimental graph of the response caused by 1.5×10−6 of C8 with electrode thickness

4 结论

本文分析了当负载为液态时，谐振器指条厚度对SAW 传感器灵敏度的影响。利用有限元商业软件建立流固耦合理论和压电耦合相结合的有液膜负载的仿真模型，结合COM 模型及P矩阵级联技术，理论计算了SAW 器件灵敏度随指条厚度的变化曲线；开展了DMMP、C7、C8 作为实验样品的响应实验测试，发现实验获得的变化曲线与理论分析得到的变化曲线大致相符合，最优归一化电极厚度为6.4%～7.6%之间。以0.0016 mg/mL DMMP 液膜负载为例，根据实验结果，指条厚度h=461.9 nm 时灵敏度最高(取均值为1685 Hz)，指条厚度h=253.7 nm 时灵敏度最低(取均值为648 Hz)，灵敏度提升了1.6 倍。该研究为GC/SAW系统中SAW检测器的优化设计提供了依据。