关于几类二阶线性微分方程的次正规解
2022-07-07谭晖肖丽鹏
谭晖, 肖丽鹏
( 江西师范大学数学与统计学院, 江西南昌 330022)
1.引言与结果
在本文中, 我们将假定读者熟悉亚纯函数的值分布理论和标准记号[1].另外, 使用记号σ(f)表示亚纯函数f(z)的增长级, 且使用记号σ2(f)表示f(z)的超级[2], 定义为

考虑二阶齐次线性微分方程

其中A和B是整函数, 我们知道方程(1.2)的每个解都是整函数.

则称f是方程(1.2)的次正规解.
高仕安和蒋翼迈定义亚纯函数的e-型级如下:
定义1[3]如果f(z)是亚纯函数, 那么f(z)的e-型级定义为

因此, 由(1.3)和(1.4)式, 可知如果σe(f)=0, 那么f是次正规的.
显然, 如果f(z)是整函数, 那么
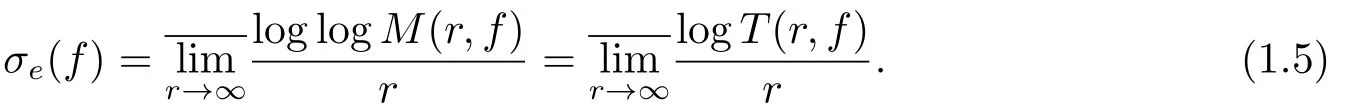
引入超级和e-型级的定义, 可以更好的判定亚纯函数f的增长性, 显然超级和e-型级有如下关系: (i)若0<σe(f)<∞, 则σ2(f)=1; (ii)若σ2(f)<1, 则σe(f)=0, 即(1.3)式成立.
但我们不能断定当σ2(f)=1时, σe(f)>0成立.
有许多学者研究了一些特殊方程解的增长性这一方面的问题[4−8], 并得到了下面的定理.

没有非平凡次正规解, 且其每一个非零解f满足σ2(f)=1.
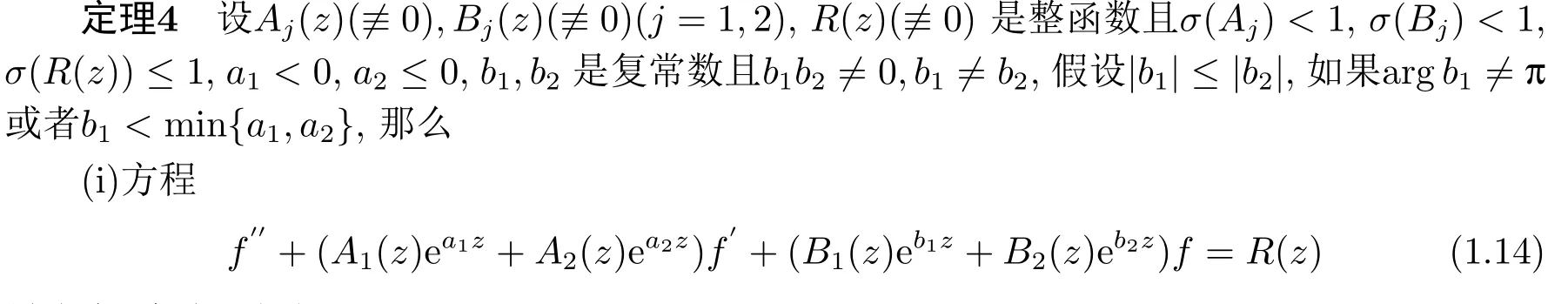
最多有1个次正规解.
(ii)方程(1.14)的所有解f满足σ2(f)=1除去(i)中可能出现的次正规解.
下面例2-6表明在定理4-7中可能存在非平凡次正规解.
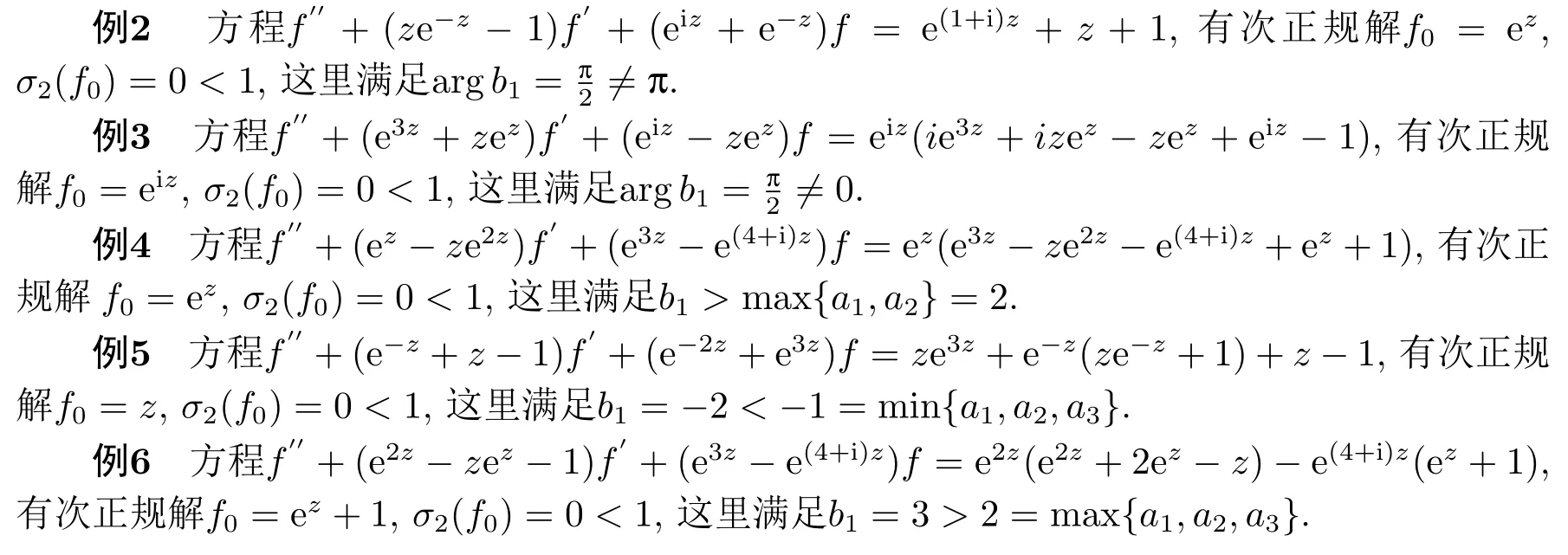
2.引理部分
引理1[4]设f是超越亚纯函数且σ(f)=σ <∞, Γ ={(k1,j1),(k2,j2),··· ,(km,jm)}是由不同整数对组成的有限集, 满足ki>ji≥0,i=1,2,··· ,m, 又设ε>0是给定的常数, 则
(i)存在零测度集E1⊂[0,2π), 使得如果ψ0∈[0,2π)E1, 则存在常数R0= R0(ψ0) > 0, 对满足arg z =ψ0及|z|≥R0的所有z及对所有(k,j)∈Γ, 有

(ii)存在对数测度为有限的集合E2⊂(1,∞), 使得对满足|z|E2∪[0,1] 的所有z及所有(k,j)∈Γ , 有(2.1)式成立;
(iii)存在线性测度有限集合E3⊂[0,∞), 使得对满足|z|的所有z及所有(k,j)∈Γ, 有


(i)如果δ(P,θ)>0, 那么
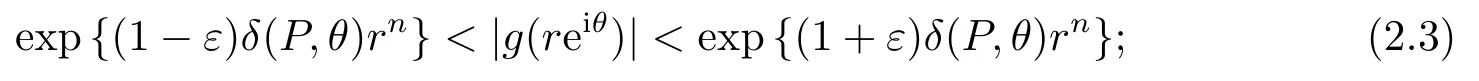
(ii)如果δ(P,θ)<0, 那么

其中H2={θ ∈[0,2π);δ(P,θ)=0}是有限集.
引理3[4]设f(z)为超越亚纯函数, α>1为一给定的常数, k,j为整数且满足k >j ≥0.
(i)存在一个对数测度有限的集合E1⊂[1,∞)和一个常数K >0, 使得对所有满足|z|=r[0,1]∪E1的z, 我们有
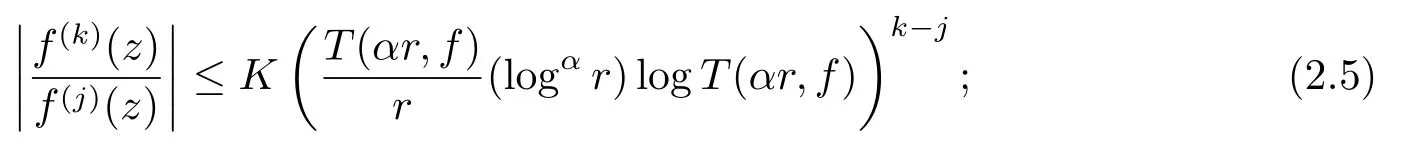
(ii)存在零测度集E2⊂[0,2π), 使得如果θ ∈[0,2π)E2, 则存在常数R = R(θ) > 0, 对满足arg z =θ及|z|≥R的所有z有(2.5)式成立.
引理4[8]设A和B是有限级整函数, 如果f(z)是方程

的解, 则σ2(f)≤max{σ(A),σ(B)}.

3.定理的证明
定理1的证明首先证σ2(f) = 1.根据引理4有σ2(f) ≤max{σ(A1eaz),σ(A0ebz)} = 1, 又由定理A知σ2(f)≥1, 故σ2(f)=1.

由引理3, 可知存在一个有限对数测度的子集E ⊂(1,∞), 和常数B > 0满足对所有满足|z|=r[0,1]∪E的z, 我们有
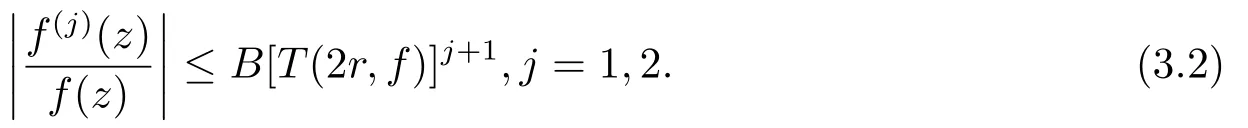
令z =reiθ, 则
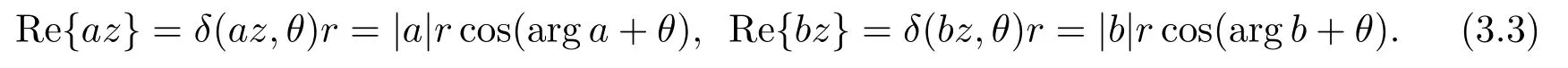
分两种情况讨论:

由(1.11)和(3.1), (3.2), (3.4), (3.5)式, 可知
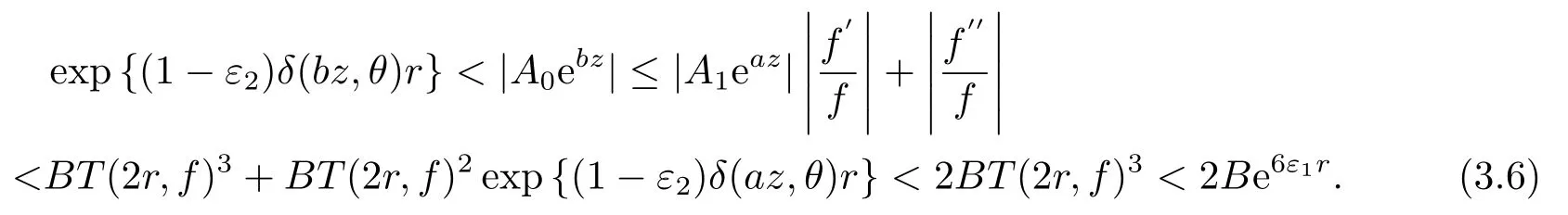
我们取0<ε2<1且0<6ε1<(1 −ε2)δ(bz,θ), 则(3.6)式不可能成立.
2) 假设a=cb(0
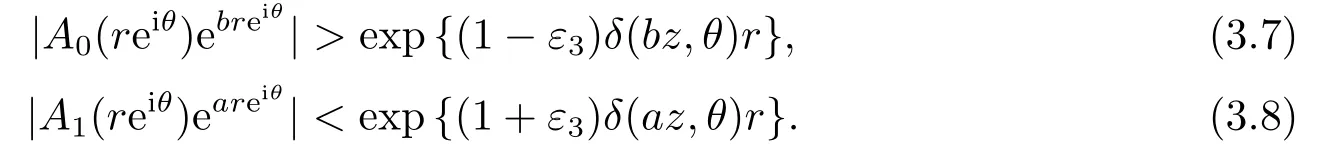
由(1.11)和(3.1), (3.2), (3.7), (3.8)式, 可知
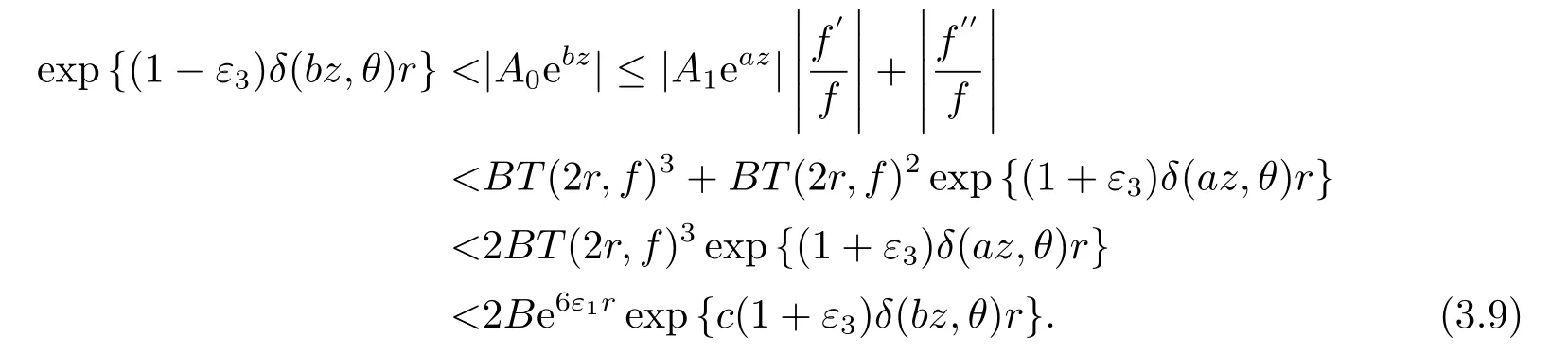
我们取0<2ε3<0<6ε1<ε3(1+c)δ(bz,θ), 则(3.9)式不可能成立, 即矛盾.
定理2的证明(i)假设f1和f2(?)是方程(1.12)的次正规解, 则f1 −f2(0)是方程(1.12)的对应齐次方程(1.11)的次正规解.这矛盾于定理1, 所以方程(1.12)最多有1个次正规解.
(ii)由定理1, 可知方程(1.12)的对应齐次方程(1.11)的所有解满足σ2(f) = 1.由常数变易法, 可知方程(1.12)的所有解满足σ2(f) ≤1.如果σ2(f) < 1, 那么f显然满足(1.3)式, 即f是次正规的.所以由(i), 可知方程(1.12)的所有解f满足σ2(f)=1 除去(i)中可能出现的次正规解.
定理3的证明假设f0)是方程(1.13)的解, 则f是整函数.由于a2≤0, 先假设a2=0.
第1步 证明σ(f)=∞.如果f是非零多项式, 由引理6, 比较方程(1.13)两边的增长性可得矛盾, 所以方程(1.13)没有多项式解.

由(3.11)和(3.17)式, 可得
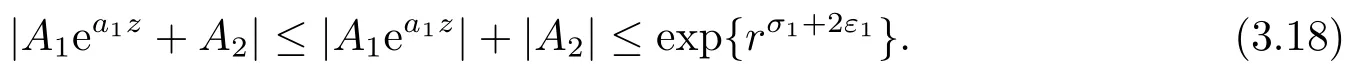
又由(3.10)和(3.15)-(3.18)式, 可得
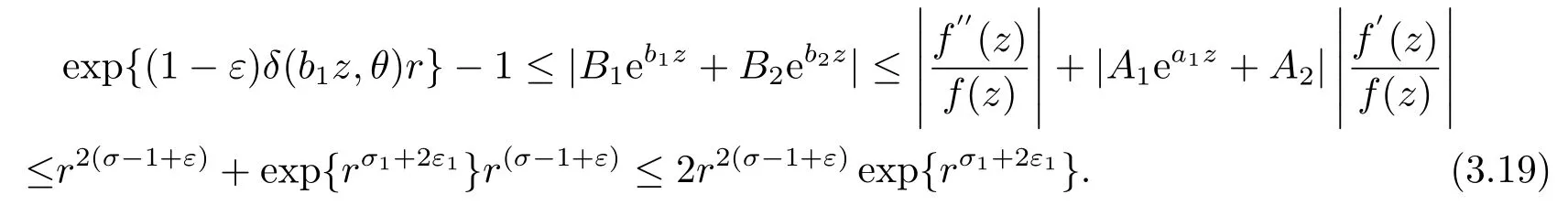
由于δ(b1z,θ)>0,0<3ε1<1 −σ1, 可知(3.19)式是一个矛盾.
当(3.13)成立时, 用类似于上述方法, 同样可得矛盾.

由于δ(b1z,θ)>0,0<3ε1<1 −σ1, 可知(3.22)式是一个矛盾.
情形2 b1

因此,

用情形1(i)的方法, 同样可得矛盾.

由(3.11)和(3.25)式, 可得

将(3.10),(3.21)和(3.26)代入(3.16)式, 可得
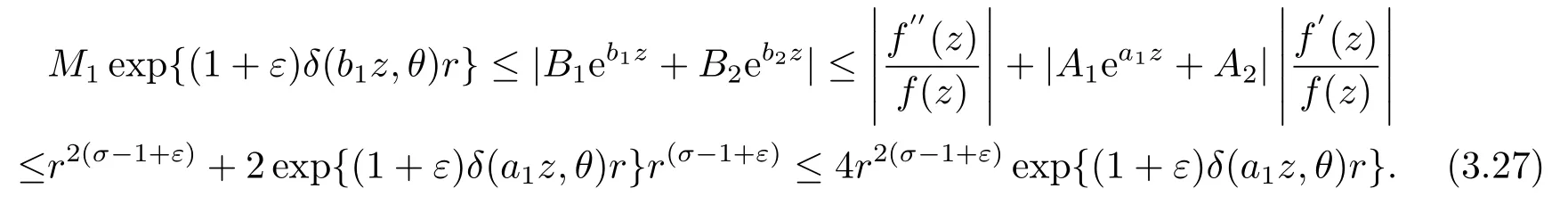
由|b1|>|a1|可知, δ(b1z,θ)>δ(a1z,θ)>0, 那么(3.27)式是一个矛盾.
综上, 可知σ(f)=∞.
第2步 证明σ2(f) = 1.由引理4和max{σ(A1ea1z+A2),σ(B1eb1z+B2eb2z)} = 1, 可知σ2(f)≤1.
根据引理3, 可知存在一个有限对数测度的子集E1⊂(1,∞)和常数B > 0满足对所有满足|z|=r0,1]∪E1的z, 我们有


由M1> 0, |b1| > |a1|可知, δ(b1z,θ) > δ(a1z,θ) > 0, 又根据超级的定义和引理7可知,σ2(f)≥1.所以σ2(f)=1.
综上, 可知σ2(f)=1.
第3步 证明方程(1.13)没有非平凡次正规解.如果f是方程的非平凡次正规解, 则f满足(1.3)式, 即对任意给定的ε2>0, 有

对于第1步中的情形1和情形2的(i), 我们有(3.30)式成立.由(3.30)和(3.32)式, 可得
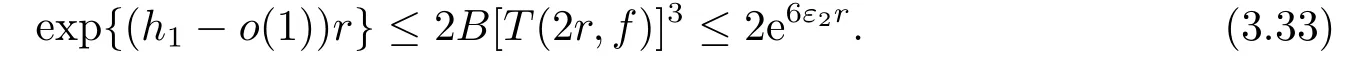
对于第1步情形2中的(ii), 我们有(3.31)式成立.由(3.31)和(3.32)式, 可得
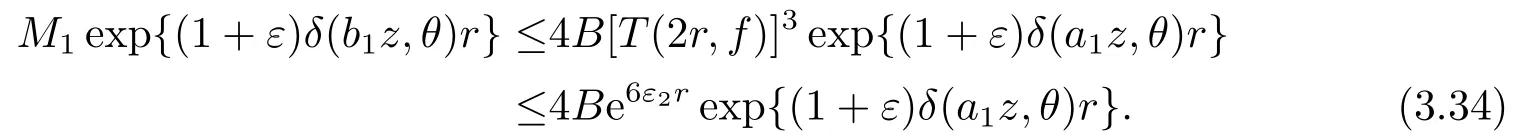
综上, 可知方程(1.13)没有非平凡次正规解.
当a2<0时, 可令a1≤a2<0, 使用类似于上面的证法, 可完成定理3的证明.
定理4的证明使用与定理2相同的证法.
定理5的证明(i)运用注2, 类似于定理3的证法; (ii)-(iii)使用与定理2相同的证法.
定理6的证明(i)假设f0)是方程(1.15)的解, 则f是整函数.由ak≤0(k =2,3,··· ,n),可分成两种情形讨论.
情形1 a2,a3,··· ,an都为零, 即ak=0(k =2,3,··· ,n), 类似于定理3的证明.
第1步 证明σ(f)=∞.如果f是非零多项式, 由引理6, 比较方程(1.15)两边的增长性可得矛盾, 所以方程(1.15)没有多项式解.

又由(3.10),(3.15),(3.36)和(3.37)式, 可得
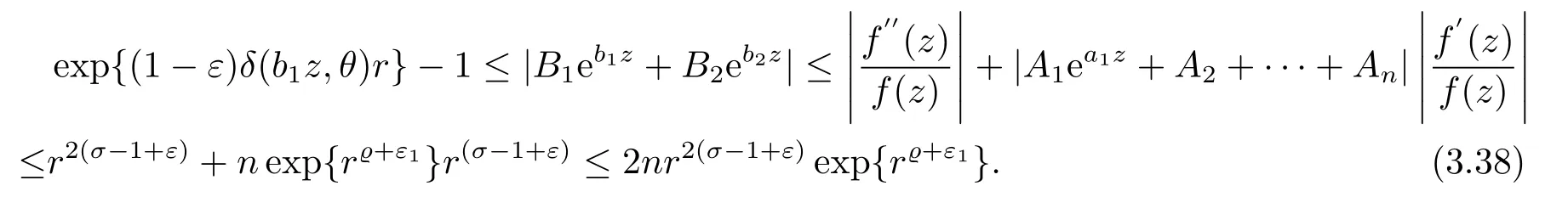
由于δ(b1z,θ)>0,0<3ε1<1 −ϱ, 可知(3.38)式是一个矛盾.
当(3.13)成立时, 用类似于上述方法, 同样可得矛盾.


由|b1|>|a1|可知, δ(b1z,θ)>δ(a1z,θ)>0, 又M1>0, 那么(3.41)式是一个矛盾.
综上, 可知σ(f)=∞.
第2步 证明σ2(f)=1.由引理4和max{σ(A1ea1z+A2+···+An),σ(B1eb1z+B2eb2z)}=1,可知σ2(f)≤1.

由M1> 0, |b1| > |a1|可知, δ(b1z,θ) > δ(a1z,θ) > 0, 又根据超级的定义和引理7可知,σ2(f)≥1.所以σ2(f)=1.
综上, 可知σ2(f)=1.
第3步 证明方程(1.15)没有非平凡次正规解.如果f是方程的非平凡次正规解, 则f满足(1.3)式, 即对任意给定的ε2>0, 有

对于第1步中的情形1.1和情形1.2的1), 我们有(3.42)式.由(3.42)和(3.44)式, 可得

对于第1步情形1.2中的2), 我们有(3.43)式成立.由(3.43)和(3.44)式, 可得

综上, 可知方程(1.15)没有非平凡次正规解.
情形2 a2,a3,··· ,an至少有一个不为零.不失一般性假设a2<0, 可令a1 (ii)使用与定理2相同的证法. 定理7的证明(i)运用注2, 类似于定理6的证法.(ii)使用与定理2相同的证法.
