奇异平面微分系统周期解的存在性

李欣,梁载涛,李胜军

(1.安徽理工大学数学与大数据学院,安徽淮南 232001;2.海南大学理学院,海南海口 570228)

1.引言

近些年, 径向对称系统的周期解及动力学行为引起了一些专家学者们的关注, 此类系统在天体力学、物理学、电磁学等应用学科中都有着广泛而又重要的应用, 因此, 研究其动力学行为具有现实意义.例如, 意大利的Fonda教授及其合作者应用拓扑度理论系统深入地研究了如下径向对称系统

周期解的存在性, 其中f ∈C(R×R+→R)关于第一个变量是周期函数且关于第二个变量在零点是奇异的.[6−11]其基本思想是通过极坐标变换, 将系统(1.1)转化为与之等价的含角动量的二阶奇异微分方程, 其结果深刻地揭示了周期解与角动量之间的紧密关系和渐进行为.值得注意的是, 此类系统和已有文献中所研究的奇异微分系统有着本质的不同, 因为该系统所隐含的角动量在其中扮演着重要作用.近几年, 国内储继峰教授等在文[2]中将研究二阶奇异微分方程周期解存在性的非线性二择一定理推广到径向对称系统(1.1), 以及刘期怀教授等在文[16]中通过对Poincar´e映射的定性分析, 探讨了一类具有排斥型奇异的径向对称系统周期解和拟周期解的存在性.此外, 关于径向对称系统(1.1)周期解稳定性的研究, 请参考文[3,14-15].

受上述文献的启发, 本文考虑如下奇异平面微分系统

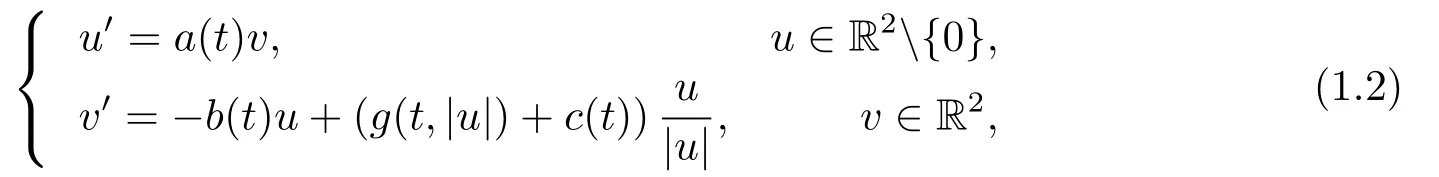
系统(1.2)在物理学中应用广泛.例如, 描述玻色―爱因斯坦凝聚体中涡旋偶极子的运动方程, 通过引入相关的变量变换, 将方程等价于形如(1.2)的奇异平面系统, 详见文[17].运用Leray-Schauder二择一定理[12], 我们将证明系统(1.2)存在一族周期解.

注意到该系统是一类径向对称系统.通过引入极坐标变换u(t) =r(t)cos ψ(t),r(t)sin ψ(t),其中r(t)>0, 极角ψ(t)∈R, 因此系统(1.3)等价于

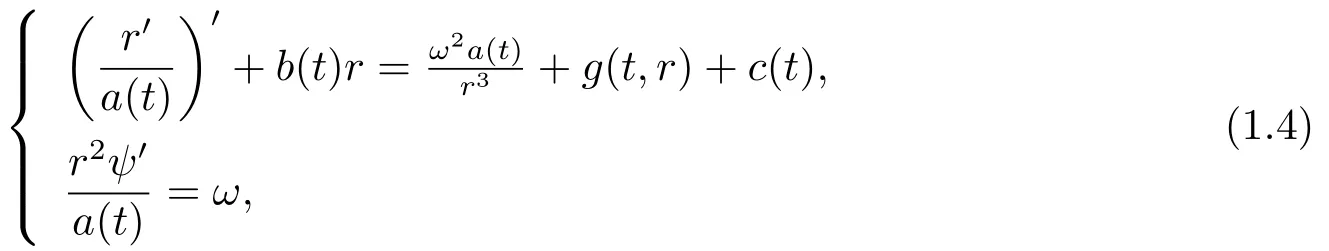
其中, ω沿着系统的解为常数.定义u的角动量为µ(t) = r2(t)ψ′(t), 由系统(1.4)的第二个等式,可得µ(t) = ωa(t).显然, 为了研究系统(1.2)径向周期解的存在性, 首先需要讨论系统(1.4)周期解的存在性.本文受储继峰教授等在文[4-5,13]中的思想和方法启发, 研究系统(1.4)周期解的存在性, 得到了一些周期解的存在性结果.在文[4-5,13]中, 储继峰教授等主要应用Leray-Schauder二择一定理以及一些不动点定理探究了不同类型的二阶奇异微分方程周期解的存在性和多解性.

本文创新之处如下: 1)将文[2]中关于二阶径向对称系统周期解的存在性结果推广到一阶奇异平面系统; 2)除了周期解的存在性, 本文还得到了周期解的一些动力学行为; 3)首次分析了周期问题(2.1)格林函数的符号.

2.格林函数的符号

考虑如下周期边值问题

首先, 回顾Sobolev不等式中最佳常数公式

其中Γ是伽玛函数.

定理2.1假设

且存在1 ≤p ≤+∞, 使得

由文[1]中推论2.3可知, 当

3.主要结果

为方便起见, 列出如下假设条件:

(H1)存在连续非负函数e(r)和h(r),使得0 ≤g(t,r)≤e(r)+h(r),∀(t,r)∈[0,T]×(0,+∞),其中e(r)>0, 且关于r单调不增, h(r)/e(r)关于r单调不减;

证首先证明∀ω >0, 系统(1.4)的第一个方程存在一个T-周期正解.为此, 先证明方程

存在一个T-周期正解r满足r(t)+ℓ(t)>0.若其成立, 则容易得到˜r =r(t)+ℓ(t)是系统(1.4)第一个方程的T-周期正解, 因为

由于(H3)成立, ∀ω >0, 选择n0∈{1,2,...}(与ω有关)满足<σRω+ℓ∗和

令N0={n0,n0+1,...}, 考虑如下一族方程

其中λ ∈[0,1],n ∈N0, gn(t,s)为截断函数, 即

显然, 寻找方程(3.3)的T-周期解与寻找下列问题的不动点等价

其中b0=1/n, Tn是全连续算子, 其定义为

因此(3.6)式中的Hω=2∥a∥∥b∥1Rω.

引理3.4∀ω >0, 存在常数δω>0, 当n充分大时, 方程(3.5)的任意T-周期解rn满足

为了证明(3.7)式, 我们先证明

引理3.5∀ϵ>0, 存在常数ω(ϵ)≥1, 若ω ≥ω(ϵ), 且r是方程(1.4)的T-周期解, 则∥r∥≥ϵ.

证反证法, 设rn是方程

下面完成定理3.1的证明.∀θ ∈[0,¯θ], 由引理3.7可知, 系统(1.2)的解满足u(t + T) =u(t)eiθ, ∀t ∈R.当θ =2π/k,其中正整数k ≥1时,由于ψ(t+kT)=ψ(t)+2π,因此,u(t)是周期的, 其最小周期为kT, 且在周期时间kT里刚好围绕原点旋转一周.则对任意正整数k ≥2π/¯θ,我们有kT-周期解, 设为uk(t), 其极坐标用(rk(t),ψk(t))表示, 令角动量µk(t) = ωka(t), 故有(ωk,rk,ψk)满足系统(1.4), (ωk,rk)∈C, 且