初始场与边界热流同时识别反问题的正则化方法
2022-07-07赵宇星徐定华
赵宇星, 徐定华
(浙江理工大学 理学院, 杭州 310018)
热传递规律广泛应用于目标体识别、 智能设计与制造领域, 如高炉炼钢、 热防护服设计、 机器制造等[1-2]. 该类问题的共性特点是通过热传导方程描述热传递现象, 给定初始温度分布和边界温度场, 研究区域内部温度场的分布. 这类热传导方程定解问题在数学上通常称为正问题.
热传导方程反问题在识别、 控制、 设计等领域应用广泛[3-4]. 文献[5-6]用Fourier正则化方法研究了热传导反问题的数值解法; 文献[7]给出了无初始值的逆时热传导反问题的数值方法; 文献[8]基于直接和伴随模型方程的迭代提出了一种求解传热反问题的算法, 使拟合泛函最小化; 文献[9]利用同伦摄动方法研究了含Neumann边界条件的热传导反问题; 文献[10-11]研究了热传导反问题转化为Fredholm积分方程系统的Tikhonov正则化理论.
本文考虑一维Neumann边界条件的热传导方程:

(1)
其中a2为热传导系数.{u0(x),f(t),g(t)}均已知的热传导定解问题(1), 称为正问题.本文讨论g(t)已知, 但{u0(x),f(t)}均未知且需确定的反问题.
反问题(IP): 利用测量的右端温度值u(l,t)|t∈[0,T]和终止时刻温度值u(x,T)|x∈[0,l], 给定g(t)|x∈(0,T], 由系统(1)确定{u0(x),f(t)}.
文献[7]利用右边界温度值的一组数据确定两个未知函数{u0(x),f(t)}, 因不具备唯一性, 故经对未知的f(t)给定先验性约束条件(即f(t)满足对称性)可使其满足唯一性.本文利用两组数据可同时反演出左边界热流密度与初始温度, 而不需要对解进行对称性先验约束.本文首先将反问题(IP)转化为不适定的第一类Fredholm积分方程组, 离散为两个病态线性方程组, 分别采用改进的Tikhonov正则化方法和BV(bounded variation)正则化方法求解连续解与非连续解; 其次, 针对误差较大的数据, 采用多次重复测量及预处理方法提高数据精度, 再经正则化方法反演初始值和边界值, 从而获得满足精度要求的近似解; 最后通过数值算例验证算法的有效性.
1 反问题(IP)的唯一性
1.1 反问题(IP)转化为Fredholm积分方程组
针对含Neumann边界条件的热传导方程定解问题, 给定右端温度值u(l,t)|t∈[0,T]和终止时刻温度值u(x,T)|x∈[0,l], 需同时反演初始温度u0(x)和左边界热流密度f(t).
文献[12]给出了正问题(1)的解:

(2)

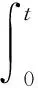

(3)
分别将x=l和t=T代入式(3)可得Fredholm积分方程组:

(4)
其中0≤x≤l, 0≤t≤T,


由上述推导可知, 反问题(IP)与方程组(4)等价.
1.2 唯一性
定理1设u0(x)∈L2[0,l],f(t)∈L2[0,T], 则反问题(IP)的解u0(x)和f(t)必唯一.
证明: 设方程组(4)有两组不同的解, 分别为(u0,1(x),f1(t))和(u0,2(x),f2(t)).记U(x)=u0,1(x)-u0,2(x),F(t)=f1(t)-f2(t), 则可得积分方程组:

(5)


(6)
将方程组(6)的第二个方程进行移项, 并化简整理可得
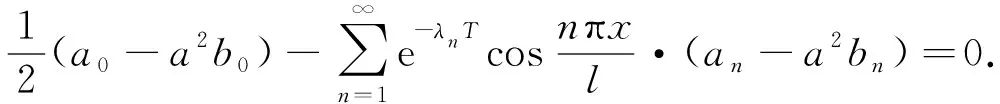
(7)


代入方程组(6)的第一个方程, 化简为

(8)
其中


注1相比于文献[7], 本文不需要对解进行对称性先验约束, 而是通过另外测量的终止时刻温度值u(x,T)|x∈[0,l]构成方程组, 保证了反问题(IP)解的唯一性.
2 反问题(IP)的数值算法
2.1 离散格式及不稳定性
取a=1, 则方程组(4)变形为

(9)
其中0≤x≤l, 0≤t≤T.
将方程组(9)中的核函数依次记为K1(t,y),K2(t,s),K3(x,y),K4(x,s), 当t 2) 利用矩形求积公式对方程组(9)中的积分进行数值求积: (10) 记 u=(u0(yj))n×1,f=(f(sj))n×1,A=(K1(ti,yj)Δy)n×n,B=(K2(ti,sj)Δs)n×n, C=(K3(xi,yj)Δy)n×n,D=(K4(xi,sj)Δs)n×n,M=(ω(l,ti))n×1,L=(ω(xi,T))n×1, 则方程组(10)的矩阵形式为 (11) 经计算当n=50时, 矩阵A,C,D的条件数均处于1018的数量级, 且节点选取越多, 矩阵A,C,D病态程度越严重, 可见反问题(IP)的不稳定性.观察到矩阵B为满秩的可逆良态矩阵, 因此可先处理矩阵B, 对方程(11)进行“消元”消去向量f, 得到关于向量u的方程: Ku=G, (12) 其中K=DB-1A-C,G=DB-1M-L.易知, 矩阵K的病态程度较严重, 需使用稳定化方法求解方程(12). 2.2 改进的Tikhonov正则化 对方程Ku=G利用Tikhonov正则化方法求解连续函数u0(x)在节点处的近似值.方程(12)的正则化解是Tikhonov泛函的极小值, 用紧算子的奇异值系统可表示为 (13) 本文采用文献[13]提出的改进正则化滤波函数: (14) (15) 2.3 BV正则化 当u0(x)不属于连续函数空间时, 本文用BV正则化方法将其转化为非线性最优化问题. TV(total variation)正则化方法是求解 (16) 本文利用一个光滑泛函逼近TV(u0), 加参数β>0得到稳定泛函, 此时全变差泛函对应的非线性优化反问题表示为 (17) 该方法通常称为BV正则化算法[14]. 为方便数值模拟, 将计算区域划分为[0,1]×[0,1]的网格.考虑u0(πx)=x2,f(t)=sin(πt),g(t)=2πcos(πt), 利用中心差商[15]对正问题(1)进行离散.正问题(1)的数值解如图1所示.在下面反问题的计算中, 将正问题的结果赋予加性噪声后作为反问题的测量数据进行数值模拟. 图1 正问题(1)的数值解u(x,t)Fig.1 Numerical solution u(x,t) of direct problem (1) 例1考虑精确解u0(πx)=x2,f(t)=sin(πt).误差水平δ分别为5%,1%,0.1%, 用改进的Tikhonov正则化方法得到数值解, 参考文献[13]取r=1.5,σ=4, 先验选取的正则化参数α=δ6/7, 反演后的初始值如图2所示, 反演后的左边界值如图3所示.由图2和图3可见, 随着测量数据误差的减小, 反演效果逐渐增强.当误差水平为5%时, 反演效果不理想. 图2 不同误差水平下单次测量反演初始值Fig.2 Initial values inversion via single measurement under different error levels 图3 不同误差水平下单次测量反演左边界值Fig.3 Left boundary values inversion via single measurement under different error levels 步骤1) 固定正则化参数α=αi, 得到关于β和误差err的图像, 其最低点坐标为(βi,erri); 固定βi, 得到关于α和误差err的图像, 其最低点坐标为(αi+1,erri+1),i=0,1,2,…,n; 步骤2) 给定ε=10-9, 当erri+1 图4 最优正则化参数Fig.4 Optimal regularization parameters 根据上述方法选取的最优参数利用BV正则化方法反演后的初始值如图5所示, 反演后的左边界值如图6所示. 由图5和图6可见, 随着测量数据误差的减小, 反演效果逐渐增强. 图5 不同误差水平下多次测量反演初始值Fig.5 Initial values inversion via multiple measurements under different error levels 图6 不同误差水平下多次测量反演左边界值Fig.6 Left boundary values inversion via multiple measurements under different error levels 求解 得到的f*,N即为经过预处理后提高了精度的数据, 最后再利用改进的Tikhonov正则化方法求解. 在误差水平为5%和1%的情形下, 加噪声函数与原函数拟合的对比结果如图7所示.图7显示了数据预处理的必要性.图8为经过数据预处理后得到的函数(σ2=0.001 6,N=30). 由图8可见, 数据预处理为增强反演效果提供了高精度的数据. 图7 不同误差水平下原函数与加噪声函数的对比结果Fig.7 Comparison results between original function and noisy function under different error levels 图8 不同误差水平下的数据预处理结果Fig.8 Data preprocessing results under different error levels 参考文献[16], 选取最优的正则化参数, 在误差水平为5%的情形下, 经过数据预处理后反演得到的初始值和左边界值如图9所示; 在误差水平为1%的情形下, 经过数据预处理后反演得到的初始值和左边界值如图10所示. 本文不考虑误差为0.1%的情形, 因为此时误差较小, 若进行数据预处理则会增加计算成本. 图9 在误差水平为5%情形下的双函数反演Fig.9 Double function inversion with error level of 5% 图10 在误差水平为1%情形下的双函数反演Fig.10 Double function inversion with error level of 1% 表1 近似解和的相对误差 综上, 本文讨论了含Neumann边界条件的热方程定解问题. 首先, 给定右端温度值和终止时刻温度值, 确定初始值和左边界值的反问题. 通过建立Fredholm积分方程组, 证明了反问题(IP)解的唯一性, 并利用改进Tikhonov正则化算法和BV正则化算法反演了初始值和左边界值; 其次, 本文对误差较大的数据先进行预处理再进行正则化; 最后, 借助MATLAB数学软件进行了数值模拟. 对于Robin边界条件, 该条件可以刻画边界有热交换的情况. 针对高维问题, 由于数据本身的复杂性及测量时不可避免的误差, 更需进行数据的预处理, 从而得到高精度的数据便于进行函数反演.







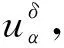




3 数值实例

3.1 连续函数重构


3.2 不连续函数重构




3.3 基于重复测量数据的函数重构







