一类相场方程的能量稳定性分析及数值模拟
2022-07-07霍俊蓉温学兵张荣培蔚喜军
霍俊蓉, 刘 昊, 温学兵, 张荣培, 蔚喜军
(1. 沈阳师范大学 数学与系统科学学院, 沈阳 110034; 2. 广东工业大学 应用数学学院, 广州 510006; 3. 北京应用物理与计算数学研究所, 北京 100088)
0 引 言
随着计算机技术的发展以及材料热力学和动力学数据的完备, 相场模型逐渐成为一种模拟各种材料微结构演化过程的重要工具. 该数值模拟方法在生物和材料力学等领域应用广泛, 如薄膜和裂纹扩展等. 在相场模型中, 需引入另一种连续的场变量以表示不同的相, 称为相场. 任意成分或结构不同的多相或多域的微观结构可通过一系列连续的场变量u表示,u随时间和空间的演化过程可由偏微分方程描述. Cahn-Hilliard方程[1]是常见的相场模型方程, 该方程在物理、 化学、 材料科学[2-3]、 热力学[4-5]、 流体力学[6-7]和图像处理[8-9]等领域应用广泛.
在不同物质相分离的过程中, 二元混合体系的2个组分自发分离, 并在各组分中形成纯畴域. 根据Ginzburg-Landau理论, 二元混合体系的自由能方程为
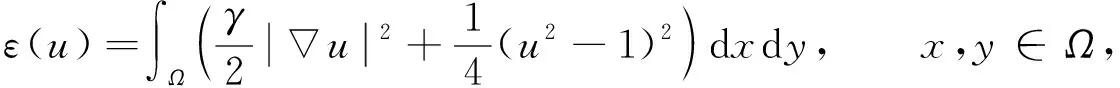
(1)
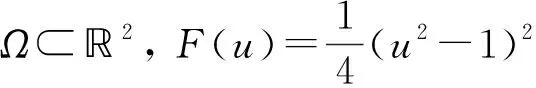

(2)
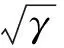
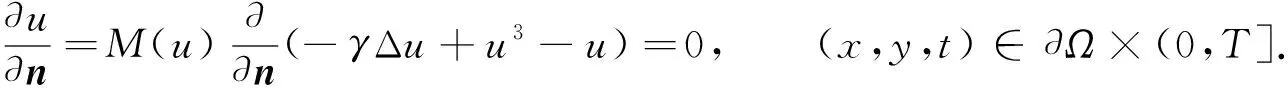
(3)
该边界条件表示区域边界上的能量流为零.
由于Cahn-Hilliard方程为四阶非线性扩散方程, 不易求得解析解, 因此, 一般借助数值方法求其近似解. 人们利用有限元方法[10-11]、 间断有限元方法[12-15]、 Lattice Boltzmann方法[16]、 最小二乘谱元法[17]和谱方法[18-19]对Cahn-Hilliard方程进行了研究. 此外, Fourier多网格算法[20]、 局部加密纯无网格有限点集法[21]和快速显式算子分裂法[22]也被应用于求解该类方程. 该类方程空间离散后得到一组刚性非线性常微分方程组, 显式时间离散方法对时间步长的限制较严格, 隐式时间离散方法允许较大的时间步长, 但需求解大型的非线性代数方程组. 本文应用有限差分方法空间求解具有恒定迁移率的Cahn-Hilliard方程, 利用Kronecker积写出二维Laplace算子的微分矩阵并将其对角化. 结合快速离散余弦变换(fast discrete cosine transform, FDCT)实现快速求解. 该方法可证明全离散格式下的离散能量保持能量稳定性, 具有存储量小和计算速度快等优点.
1 数值方法
在热力学中, 相场模型通过数值求解演化方程, 得到场变量在模拟区域和时间节点上的值, 进而反映材料体系的微结构演化过程[23]. 场变量u的演化方程通常为非线性偏微分方程, 本文采用有限差分法以及Crank-Nicolson方法, 以变量离散取值后对应的函数值近似微分方程中独立变量的连续取值, 进而求解Cahn-Hilliard方程, 该方法在解决相场模型问题的同时可保证解的稳定性.
1.1 有限差分方法
考虑迁移率M(u)=1的Cahn-Hilliard方程, 则式(2)等价于
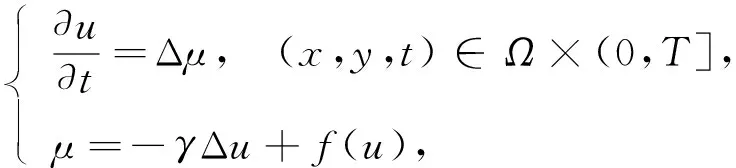
(4)
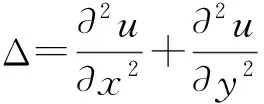
网格步长为hx=(a-b)/Nx,hy=(c-d)/Ny.在每个网格节点处有其特定的场变量.设u在网格节点(xi,yj)的数值解为ui,j(1≤i≤Nx, 1≤j≤Ny), 定义离散解ui,j为Nx×Ny阶的矩阵U.由齐次Neumann边界条件, 以及网格内部点(xi,yj)和边界处的二阶导数差分格式, 得到该方程在x,y方向的微分矩阵分别为
将解矩阵按列向量化后得
U=vec(U)=(u1,1…uNx,1,u1,2…uNx,2,…,u1,Ny…uNx,Ny)T.
(5)
设Ix,Iy分别为Nx,Ny阶单位矩阵, 利用微分矩阵Bx和By以及Kronecker积的定义[24], 可将式(4)的中心差分格式写为
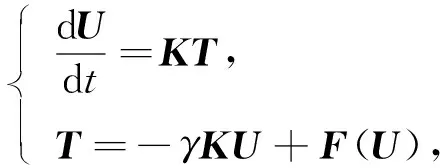
(6)
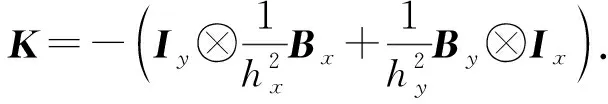
引理1对分别为Nx×Nx阶与Ny×Ny阶的正交矩阵Cx与Cy, 矩阵Bx与By有如下的特征分解:

(7)


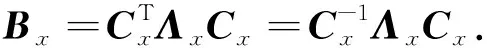
(8)
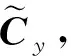
引理2对N阶矩阵X以及N阶矩阵A,B,C,D, Kronecker积有如下性质[26]:
1) (A⊗B)(C⊗D)=AC⊗BD;
2) (A⊗B)-1=A-1⊗B-1;
3) (BT⊗A)vec(X)=vec(AXB);
4) (A⊗B)T=AT⊗BT.
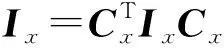
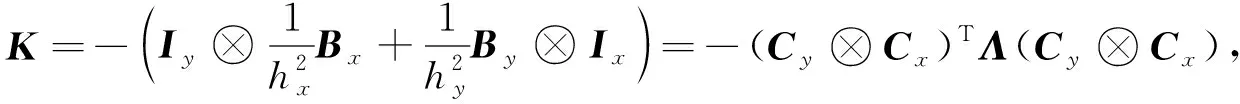
(9)
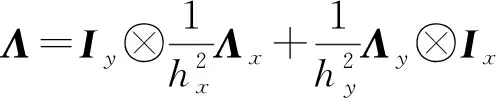
引理3K为对称负定矩阵, 且可分解为K=-LTL.
由引理3可得:
引理4对∀U∈Nx×Ny, 有(KU,U)=-‖LU‖2, 其中‖·‖为Euclid范数.
1.2 Crank-Nicolson方法
Cahn-Hilliard方程为四阶非线性方程, 显式时间离散方法对时间步长的限制较严格, 隐式格式具有较好的稳定性. Crank-Nicolson方法是常用的二阶隐式差分格式, 一般用于求解具有守恒型的非线性方程. 下面应用Grank-Nicolson差分方法对空间离散后得到的式(6)进行时间离散, 得
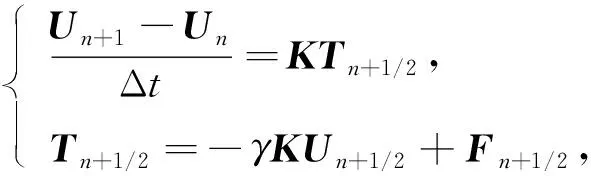
(10)
式(10)可等价为
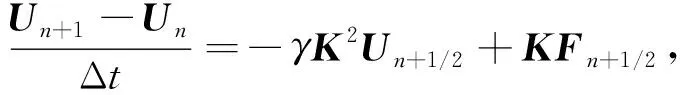
(11)
其中
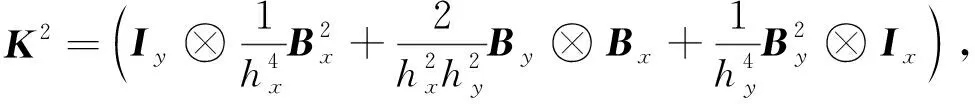
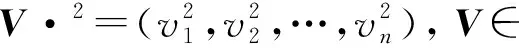
由式(1), 定义离散自由能形式为
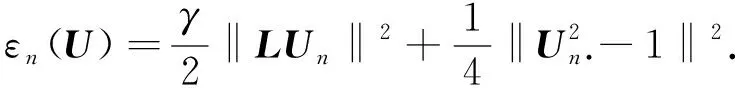
(12)
将式(10)中的两式分别与Tn+1/2和Un+1-Un做内积, 可得
(Un+1-Un,Tn+1/2)=(KTn+1/2,Tn+1/2)=-‖LTn+1/2‖2,
(13)
(Tn+1/2,Un+1-Un)=(-γKUn+1/2,Un+1-Un)+(Fn+1/2,Un+1-Un).
(14)
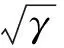
对Tn+1/2=-γKUn+1/2+Fn+1/2两端与Un+1-Un做内积, 可得
(Tn+1/2,Un+1-Un)=(-γKUn+1/2,Un+1-Un)+(Fn+1/2,Un+1-Un).
(15)
对式(15)右端两式分别进行运算, 有
则可将式(15)化为
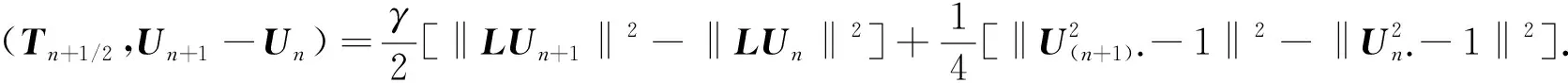
(18)
由(Un+1-Un,Tn+1/2)=-‖LTn+1/2‖2以及二元混合体系的自由能ε(u)的定义, 可得
εn+1(U)-εn(U)≤0.
(19)
由式(19)可知, 在零通量边界条件下, 有εn+1(U)≤εn(U).即离散形式的自由能具有关于时间非增的性质.
由于相场模型满足一种被称为能量稳定的非线性稳定关系, 即自由能泛函随时间递减.因此, 本文的数值格式可在快速求解的同时满足离散能量稳定.
1.3 快速实现
下面应用FDCT快速求解全离散后的Cahn-Hilliard方程, 即式(11). 利用数值方法结合初始值与边界条件, 求解与微分方程对应的离散数值解, 进而描述二元合金的凝固、 固态相变、 电子迁移、 粗化与晶粒生长等物理现象的演化过程.
首先对其进行整理得

(20)
令C=Cy⊗Cx, 可将矩阵K和K2对角化, 得到K=-CTΛC,K2=CTΛ2C, 结合式(14), 可将式(20)写为
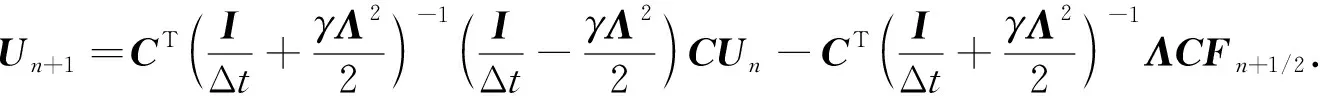
(21)
分三步求解式(21).
1) 计算CUn与CFn+1/2, 由引理2的性质3)可得
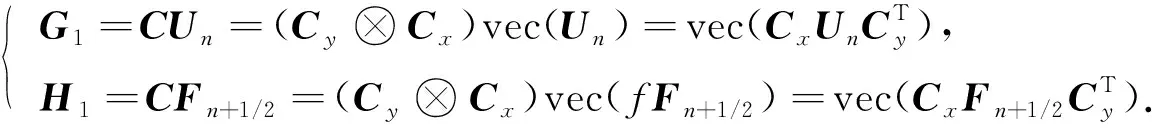
(22)
式(22)可由MATLAB中命令dct2实现.这里向量G和H分别由矩阵G和H向量化得到, 即G=vec(G),H=vec(H).
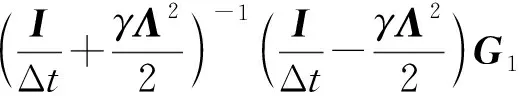
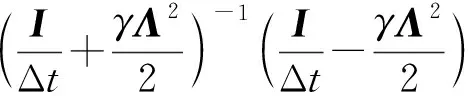
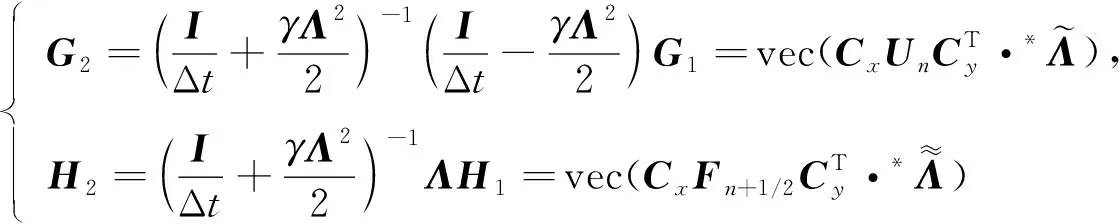
(23)
实现.
3) 计算CTG2和CTH2, 利用引理2中的性质2)和性质3), 可得
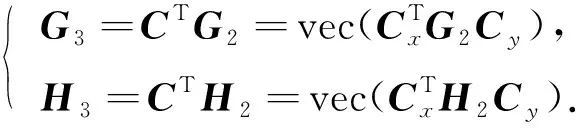
(24)
式(24)可由MATLAB中命令idct2实现.非线性代数方程组(20)可写为
Un+1=G3-H3.
(25)
当
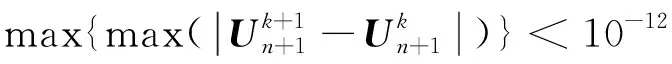
(26)
时, 迭代结束.
2 数值实验
求解具有初始条件u0(x,y)=0.1sin(x)sin(y)的Cahn-Hilliard方程(4), 并验证其自由能关于时间是非递增的.
将其网格剖分为64×64, 时间离散步长为0.01, 过渡区域厚度γ=0.01.离散形式质量与能量随时间的变化曲线如图1所示.由图1可见, 在全离散格式下, 质量守恒且自由能关于时间是非递增的.因此, 本文采用的数值方法可在离散后保持Cahn-Hilliard方程的本质特征, 并保证全离散格式解的稳定性.
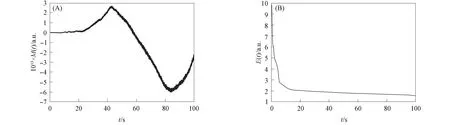
图1 离散形式质量(A)与能量(B)随时间的变化曲线Fig.1 Change curves of discrete mass (A) and energy (B) with time
为更好展示二元合金中金属部件浓度的相分离过程及其粗化过程, 在[0,2π]2求解区域中求解初始条件为
的算例, 其中u为二元合金中金属部件浓度.将求解区域网格剖分为128×128, 取计算时间T=2, 时间步长Δt=10-4, 金属部件浓度过渡区域的参数γ=0.01.不同时间下的二元合金中金属部件浓度如图2所示.由图2可见, 浓度变化包含2个阶段.第一个阶段为相位分离, 通常由自由能εn(U)的最小化引起, 使浓度在0 图2 不同时间下的二元合金中金属部件浓度Fig.2 Concentration of metal parts in binary alloys at different time 为验证本文的数值方法可在保证稳定性的同时提高计算效率, 将网格剖分成不同大小, 对是否采用FDCT的计算时间进行比较. 取时间步长Δt=10-4, 最终计算时间T=0.005.在不同网格剖分条件下, 采用FDCT和未采用FDCT的CPU时间列于表1. 由表1可见, 本文结合FDCT使计算效率得到极大提高. 表1 采用FDCT和未采用FDCT的CPU时间比较 综上, 本文在空间和时间上分别应用有限差分方法和Crank-Nicolson方法对具有恒定迁移率的Cahn-Hilliard方程进行全离散. 利用Kronecker积写出二维Laplace算子的微分矩阵, 并引入Kronecker积的性质将微分矩阵进行特征分解. 在实现过程中, 采用不动点迭代法结合快速离散余弦变换求解, 以提高计算效率. 本文结合微分矩阵的性质证明了全离散格式下的Cahn-Hilliard方程仍保持其离散能量不增, 通过数值实验验证了该方法的稳定性.