基于高斯混合模型的无线传感器网络定位算法

方 省, 罗 引, 曹 家, 徐 楠, 蒋水宾, 郝艳妮

(1. 天津大学 经济与管理学院, 天津 300072； 2. 中国科学院自动化研究所, 北京 100190；3. 北京中科闻歌科技股份有限公司, 北京 100000)

随着物联网[1-3]和智慧城市建设的快速发展, 人们对位置服务需求与日俱增. 无线传感器网络(wireless sensor networks, WSNs)位于物联网(internet of things, IoT)的感知层, 节点的定位信息是物联网实现和普及的基础和前提[4]. 距离信息可先由TOA[5],AOA[6],TDOA[7-8],RSSI[9],DV-Hop[10-11]和DV-distance[12]等技术计算得出, 然后通过三边测量法等定位方法计算未知节点的位置. 但由于非视距问题[13-14](NLOS)、 定位环境及路径传播模型等因素影响, 测量的距离通常存在一定的误差[15].

针对距离误差对定位的影响, 目前已有许多方法可降低误差的影响： 1) 根据定位环境改善路径损耗模型参数, 进行实时估计, 如文献[16]提出了一种多模型选择算法, 在分析路径损耗模型统计特性的基础上, 提出了一种进行路径损耗模型的量化方法, 文献[17]提出了一种根据环境变化的RSS室内定位方法； 2) 根据某些方法, 对于不同的测距信息给予不同的权值, 如文献[18]引入了多个通信半径以细分跳数, 并推导了跳数随半径变化次数的公式, 通过校正加权值修正平均跳数距离对平均跳距离进行加权处理, 文献[19]采用最小均方误差和逆距离加权法处理平均一跳距离； 3) 采用某种算法筛选出含有误差的测距信息, 将其从距离信息中去除. 但在实际应用中, 方法1)过于繁琐和复杂, 方法2)效果不佳, 定位结果仍存在较大误差.

基于此, 本文提出一种基于高斯混合模型的无线传感器网络定位算法, 以解决不准确距离信息对定位结果的影响. 通过构建混合高斯模型并分析筛选出误差较大的距离信息, 将其从距离信息集合中剔除, 再对剩余的距离信息集合利用三边测量法和加权算法计算未知节点的位置. 仿真实验结果表明, 利用改进算法对距离信息处理, 剔除大误差距离信息后, 所得到的定位结果更精准, 误差更小.

1 高斯混合模型及其参数估计

本文使用高斯混合模型(Gaussian mixture model, GMM)拟合由三边测量法[20-22]得到的定位结果集合, 通过模型分析, 找出远离中心的定位结果及定位这些位置所使用的距离信息, 并删除出现次数较多的距离信息, 利用剩余的距离信息进行位置估计. 假设p(y|θ)为定位结果的概率密度函数, 则

用高斯混合模型拟合定位结果就是将这些定位结果进行分类, 各类别的概率密度函数可视为一个服从高斯分布的函数.常用的高斯混合模型参数估计算法是最大似然估计和最大期望(EM)算法.

算法1高斯混合模型参数估计的EM算法.

输入: 观测数据y1,y2,…,yN, 高斯混合模型；

输出： 高斯混合模型参数;

步骤1) 取参数的初始值开始迭代;

步骤2) E步： 根据当前模型参数, 计算分模型k对观测数据yj的响应度为

步骤3) M步： 计算新一轮迭代的模型参数为

步骤4) 重复步骤2)和步骤3), 直到|p(y|θ)-p(y|θ)′|<ε, 其中p(y|θ)和p(y|θ)′为相邻两次迭代的结果, 即前后两次迭代的结果小于一定程度即可终止迭代, 通常ε=10-5.

2 算法设计

为证明高斯混合模型无线传感器网络定位算法的合理性和有效性, 本文先介绍三边测量法并分析不准确距离信息对定位结果的影响, 以证明提出的算法可提高定位精度.

由于受环境和非视距问题(NLOS)等因素的影响, 测得的距离与真实距离通常有一定的误差. 为全面分析不准确信息对定位的影响, 分别从不准距离信息的程度(即不准距离信息所含误差大小)及不准距离信息多少(即不准距离信息占总距离信息的比例)两方面进行分析和对比.

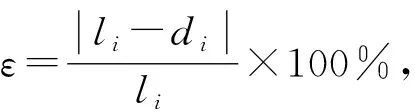
图1为当不准距离信息个数m=2时, 定位结果的误差随不准距离信息程度变化的情况. 由图1可见, 当ε>10%时, 随着ε的增大, 定位误差(RMSE)也随着增大； 当ε>30%时, 由于距离信息所含误差过大, 导致三边测量定位误差显著上升.

图1 不准程度对三边测量法的影响Fig.1 Effect of inaccuracy on trilateral measurement

不准距离信息多少对定位结果的影响是指不准距离信息占全部距离信息比例的不同会导致定位结果的不同.为方便, 本文用η表示不准信息占全部距离信息的比例, 仿真场景设置与不准距离程度的仿真条件相同.仿真条件设置： 不准程度ε=5%,10%,20%,30%,m的取值范围为0≤m≤6, 即η从0变化到40%, 由于当η>40%时, 测距信息集中有近1/2的距离信息不准确, 此时定位系统性能非常差, 故对m>6的情况进行仿真无意义.

图2为不同测距误差ε下不准距离信息大小对三边测量结果的影响.由图2可见, 随着不准程度ε的增高, 定位误差随之增加； 在不准程度ε确定的情况下, 随着不准距离信息数目的提高, 定位误差也随着增加； 剔除不准距离信息后, 利用三边测量法对剩余距离信息进行定位, 定位结果较精确.因此, 不准确距离信息增加了定位结果的误差, 降低了定位的精准度.从距离集合中剔除误差大的距离信息, 利用剩余的距离信息进行三边测量法定位, 将会使定位结果更精确.

图2 不同测距误差ε下不准距离信息大小对三边测量结果的影响Fig.2 Effect of inaccurate distance information on trilateral measurement results under different ranging errors ε

三边测量法需要3个距离信息, 当距离信息集合中多数距离都在合理的误差范围内时, 通过三边测量法得到的一系列定位结果之间的差距很小, 它们集中在一片密集的区域.但当测距信息中含有较大误差, 即通过三边测量所对应的3个距离信息只要有一个含有较大的误差时, 则所得到的位置将偏离该区域, 本文据此通过高斯混合模型分析对偏离密集区域的定位结果进行分析, 剔出大误差距离信息.

高斯混合模型中K值的选择对定位精度和运行时间有影响, 子高斯模型过多会延长算法的运行时间, 对位置样本点A中样本的分析将更详细, 定位精度有所提高； 子高斯模型过少会缩短算法的运行时间, 但模型过于简单, 对于位置样本点A中样本的分析会粗糙, 定位精度低.通过仿真实验可知选择K=2最合适.

定位结果高斯混合模型建立的过程： 概率密度函数为

基于上述分析, 本文利用高斯混合模型对三边测量法得到的一系列定位结果建模, 并对建模结果进行分析, 可知集合B和C所含的定位结果偏离真实定位结果, 根据一个定位结果中含有3个距离信息, 分析可得B和C所含有的距离信息有较大误差, 再通过反向分析可得出含有误差较大的距离信息.将误差较大测距信息从距离信息集合中剔除, 利用剩余距离信息集合进行定位分析和计算.该方法必须满足已知位置节点数目必须超过6个, 这样通过三边测量方法将会产生足够多的定位结果样本, 而锚节点多于6个的情况在应用中是普遍现象[19].

加权定位算法表示为对定位集合A, 假设由任意3个节点通过三边测量法得到的未知节点坐标为(xn,yn), 其由di,dj,dk三个测距信息获取, 针对定位集合A的加权定位算法[18]求得节点(x,y)为

基于高斯混合模型的定位算法步骤如下：

2) 根据高斯混合模型输出的最终结果找出元素个数最少的子高斯模型φ2, 其含有的定位结果集合为B和距离φ1中心最远的定位结果集合C;

3) 找出集合B和C中定位结果所包含的点, 由于每个点对应着3个距离信息, 通过分析找出所对应距离信息集合中出现频率最高的前m个距离信息, 假设d1,d2,…,dm即为误差较大的距离信息;

4) 对剩余的距离信息进行三边测量法, 得到一系列定位结果, 对其进行高斯模型拟合, 得高斯模型的均值μ=(μx,μy), 对定位结果进行加权定位, 用(x,y)表示;

本文取δ=0.5 m.阈值的设置使算法适应性更强, 若m设置过小, 则不能将不准确距离信息全部剔除, 需通过估计位置与高斯模型中心的欧氏距离判断是否需要继续剔除不准确信息, 使得出的定位精度更高, 与真实值的位置更接近.

3 仿真实验

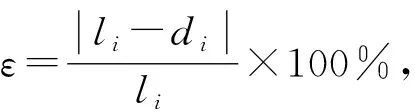
(1)

3.1 不同测距误差分布下算法的有效性

仿真环境设置： 将锚节点随机分布在100 m×100 m的监测区域中, 未知节点U位于坐标为(50,50)位置处, 假设未知节点能接收与15个锚节点的距离信息.

在本文仿真场景中, 未知节点接收到的15个距离信息{d1,d2,…,d15}所包含的误差εi(i=1,2,…,15)(当ε>50%时, 测距误差较大, 对定位结果影响过大, 故仿真不予考虑)分别服从均匀分布和正态分布, 仿真结果如图3所示.由图3可见, 无论测距误差服从均匀分布还是正态分布, 所得定位结果均较相近.从而验证了在不同测距误差分布下本文算法都有效.

图3 不同测距误差分布下定位结果的对比Fig.3 Comparison of positioning results under different ranging error distributions

表1为计算中m分别取1,2,3, 高斯混合建模分析剔除误差较大的1,2或3个信息(该仿真算法不包含基于高斯混合模型定位算法中的步骤5)进行自适应调整m值), 然后使用三边测量法和加权算法求其定位结果.

表1 当测距误差服从不同分布时, 两种算法定位误差的仿真结果

由表1可见, 无论测距误差ε服从均匀分布还是正态分布, 改进算法对于测距信息中不存在不准距离信息的情况也适用.当m增大时, 去除误差大的前m个测距信息, 随着m的增大, 改进算法所得的定位结果与真实定位结果更接近.

3.2m值对定位结果的影响

当m设置过小时, 算法会根据定位结果与聚类中心的欧氏距离进行调节, 其对定位结果的影响较小, 只需多次迭代花费更多的时间； 如果m设置过大, 大于含有不准距离信息的个数时, 考虑是否会对定位结果产生影响.不失一般性, 仿真环境与3.1相同, 不准确距离信息数目n=3,ε=20%, 分别取m=1,2,3,4,5, 然后使用三边测量法和加权算法求其定位结果, 定位误差仿真结果列于表2.

表2 当m取不同值时不同算法定位误差的仿真结果

由表2可见: 当m=1,2,3时, 定位结果非常接近, 验证了算法对于阈值δ设置的合理性; 当m=4,5时, 虽然大于不准确距离信息的个数, 但对于定位结果的影响较小, 误差波动不大.验证了在合理的取值范围内,m的取值不会对定位结果有较大影响.

3.3K值对定位结果的影响

K值的大小将对定位精度和运行时间产生影响, 为得出合适的K值进行仿真对比. 仿真环境与3.1相同, 不准确距离信息数目n=3,ε=20%.当K值分别取2,3时, 计算其RMSE, 结果列于表3. 由表3可见, 当K=3时, 定位误差比K=2时小, 但其波动浮动较小, 而运行时间延长浮动较大, 权衡两者对定位的影响, 本文选择K=2.

表3 当K=2,3时不同算法定位误差的仿真结果

3.4 改进算法与三边测量法的定位精度对比

针对在不同误差ε和不同大误差测距信息数目的情况下, 为验证改进算法的有效性和实用性, 进行改进定位算法和三边测量法所得定位误差的仿真对比, 结果如图4所示. 仿真环境与3.1相同.

图4 定位误差随不准距离信息个数的变化Fig.4 Positioning errors vary with number of inaccurate distance information

由图4可见： 随着测距误差增大, 大误差测距信息数目增多, 三边测量定位法受到的影响越大, 性能下降, 导致定位误差越大, 精度更低; 改进定位算法所得定位结果基本不随大误差测距信息的增大而增大, 在测距误差逐渐增大和不准测距信息数目逐渐增多的情况下, 改进定位算法剔除大误差测距信息后, 定位误差有明显减少, 提高了定位精度.

3.5 DV-Hop算法的仿真分析

为验证改进定位算法应用的广泛性和合理性, 将改进定位算法应用到DV-Hop算法中, 对改进DV-Hop算法与原始DV-Hop算法所得定位误差进行对比, 结果如图5所示. 仿真环境参数设置为： 在80 m×80 m的区域上布置80个节点, 通信半径分别为20 m和30 m, 其中K=2, 考虑到锚节点数目的不同, 当锚节点数目小于10时m设置为2, 当锚节点数目大于10小于20时m设置为3, 当锚节点数目大于20小于30时m设置为4, 当锚节点数目大于30小于40时m设置为4.

图5为当通信半径R=20,30 m时改进的DV-Hop算法与原DV-Hop算法的定位精度随锚节点数目变化的情况. 由图5可知： 通信半径R=30 m大于R=20 m时的定位精度, 这是因为当通信半径增大时, 未知节点可通信的锚节点数目增多, 即得到的测距信息更多, 当测距信息更多时可获得的定位结果更精确； 改进DV-Hop定位算法的定位误差远小于原DV-Hop算法的定位误差, 这是因为改进算法提高了定位精度, 使定位结果与真实定位结果更接近.

图5 当R=20,30 m时不同算法定位精度随锚节点个数的变化Fig.5 Positioning accuracy of different algorithms changes with number of anchor nodes when R=20,30 m

综上所述, 本文在分析不准确距离信息对定位影响的基础上, 结合高斯混合模型提出了一种提高定位精度的定位算法. 该算法通过高斯混合模型拟合定位结果, 剔除大误差测距信息, 结合三边测量定位法对剩余的距离信息集合得到定位估计集合, 再对定位估计集合进行加权处理, 得到离未知节点真实位置较近的坐标. 仿真结果表明, 改进算法削弱了不准测距信息对定位结果的影响, 定位精度有显著提高, 与真实位置更接近.