非均匀介质内障碍反散射的Bayes方法
2022-07-07尹伟石尹运文孟品超
尹伟石, 尹运文, 孟品超
(长春理工大学 理学院, 长春 130022)
非均匀介质中不可穿透障碍物反散射问题在医学探测、 地球物理勘探和非破坏性实验等领域应用广泛. 目前, 在反散射问题的研究中已有许多方法可重构障碍物或非均匀介质[1-4], 但同时重构非均匀介质和嵌入障碍物的研究文献报道较少. 对于该类问题, 文献[5]用牛顿迭代法同时重构非均匀介质、 嵌入障碍物的边界以及边界条件; 文献[6]用传统线性采样方法重构出外部的非均匀介质, 由于传统线性采样法无法重构出内部嵌入障碍物的信息, 因此需通过改进的线性采样法重构嵌入障碍物.
近年来, 随着计算机技术的进步与发展, 以Bayes理论为基础的反问题求解方法已引起人们广泛关注. Bayes方法可从统计角度思考反问题. Stuart[7]首次提出了反问题下的Bayes理论框架, 并给出了反问题Bayes方法的适定性定理; Bui-Thanh等[8]证明了声波障碍反散射中形状重构问题的Bayes方法适定性; 基于文献[8], Wang等[9]用Bayes方法求解了一类腔体反散射问题; Li等[10]将扩采样方法与Bayes方法相结合求解有限孔径反散射问题, 先用扩采样方法重构障碍物的位置, 再用Bayes方法重构障碍物的形状. 上述研究均考虑有相位的情形, Yang等[11]进一步将Bayes方法应用到无相位反散射问题求解中. 本文针对非均匀介质内障碍反散射问题, 用Bayes方法同时重构非均匀介质的交界面和嵌入障碍物.
1 正问题
正问题的几何模型如图1所示. 设Ω⊂2表示非均匀介质的支集且具有Lipschitz边界Γ0,Ω内的折射率为n(x)∈L∞(Ω), 且Ren(x)>0和Imn(x)≥0.表示非均匀介质外部的均匀介质, 且Ω0内折射率n0=1.设D⊂⊂Ω表示嵌入在非均匀介质内部的声软障碍物, 具有C2,α边界Γ1, 且
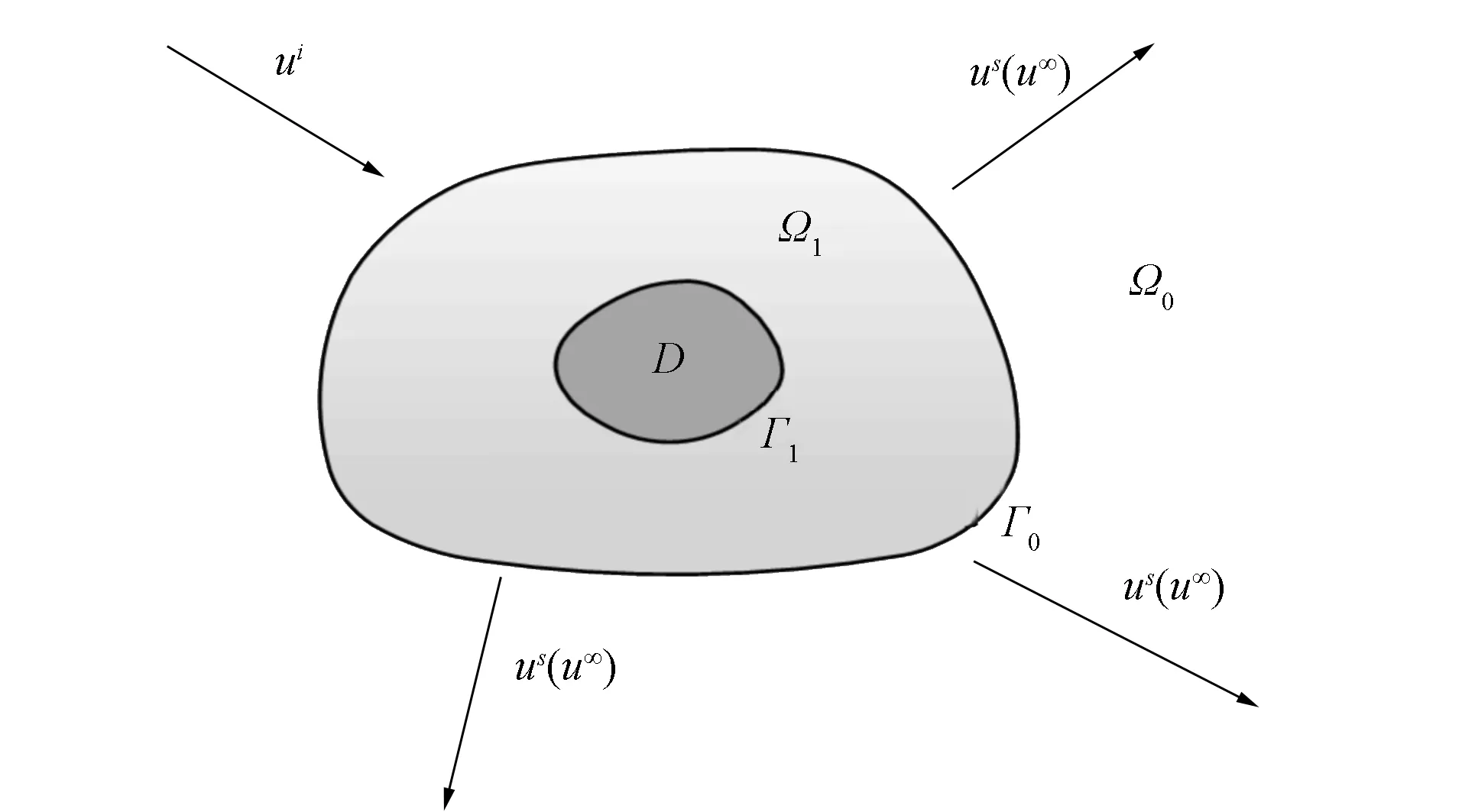
图1 正问题的几何模型Fig.1 Geometric model of positive problem
和
分别表示Γ0的外部散射总场和内部散射总场.给定入射平面波, 考虑如下Helmholtz系统:
其中k>0为波数,v0为Γ0的单位外法向量,λ为取决于介质Ω和Ω0的传输系数.
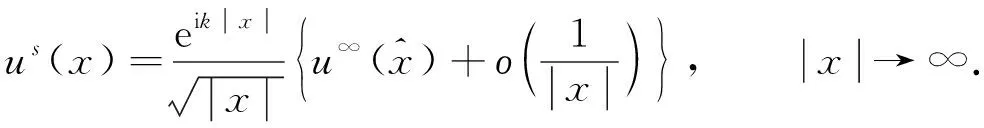
(6)
2 Bayes方法
用全孔径远场数据和有限孔径远场数据同时重构交界面Γ0和障碍物边界Γ1的Bayes方法.
2.1 先验分布
非均匀介质和内部嵌入障碍物由交界面Γ0和边界Γ1决定,Γ0和Γ1可通过有限集合P和Q形式分别进行参数化
P∶=(p1,p2,…,pN1)T∈N1,Q∶=(q1,q2,…,qN2)T∈N2,
(7)
记Z∶=(P,Q)∈N,N=N1+N2.设{zn}(n=1,2,…,N)是相互独立的Gauss变量,zn满足
zn~N(mn,sn),n=1,2,…,N,
(8)
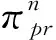
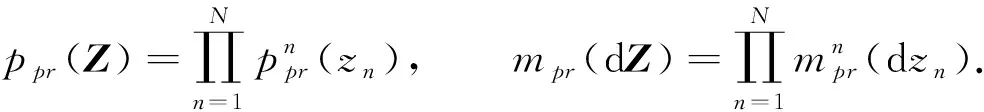
(9)
为便于计算, 假设m1=…=mn=mpr,s1=…=sn=spr,n=1,2,…,N, 即{zn}(n=1,2,…,N)是独立同分布的Gauss变量.
2.2 后验分布
考虑入射场形式为

(10)
其中入射方向dl∶=(cosαl,sinαl), 入射角度α均匀分布在[0,2π)内,
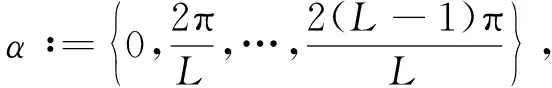
(11)
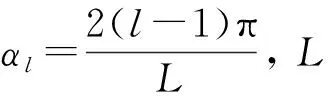
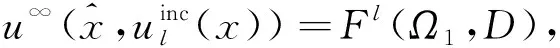
(12)

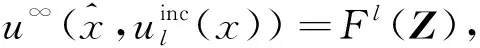
(13)
式(13)表明非线性观测算子Fl可视为交界面和嵌入障碍物的参数空间到散射远场空间的一个抽象映射, 且Fl:N→C(S1).进一步, 可将统计模型写为
Yl=Fl(Z)+ηl,
(14)
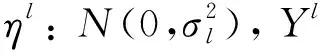
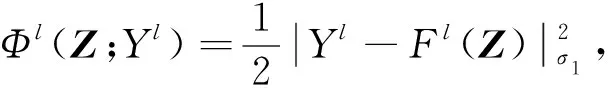
(15)
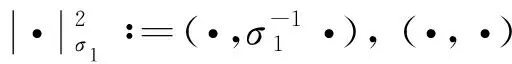
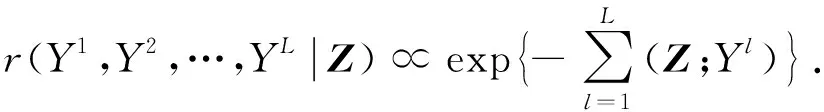
(16)
根据Bayes公式可求得后验概率密度为
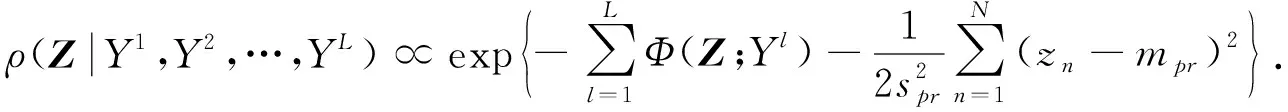
(17)
求解反问题MCMC(Markov chain Monte Carlo)算法的流程如下:
1) 初始化Z(0),β∈(0,1)为一个常数,K为最大迭代次数;
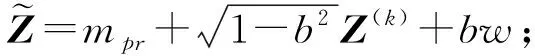
5) 重复步骤2~4)至K次.
3 数值算例
下面通过数值算例验证Bayes方法的有效性.在所有数值实验中均假设:
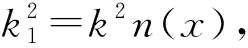
2)Γ0和Γ1的未知参数服从分布的均值mpr=0和标准差spr=1, 对于观测误差ηλ满足s1=…=sl=serror,l=1,2,…,L;
3) MCMC算法最大迭代次数K=10 000, 取最后1 000个样本的均值作为参数反演结果;
4) 用实线表示Γ0和Γ1的真实曲线信息, 用虚线表示Γ0和Γ1的重构曲线信息.
实验1考虑交界面Γ0为椭圆x(t)=(0.1,0.1)+(4cost,3sint), 嵌入障碍物边界Γ1为风筝x(t)=(-0.5+cost+0.65cos 2t,-0.5+1.5sint),n(x)=4, 波数k和k1分别为0.5和1,serror=0.01, 观测孔径为[0,2π].Γ0和Γ1的参数形式Z可表示为
Z∶=(z1,z2,…,z9)T,

图2 z1的后验分布直方图Fig.2 A posteriori distribution histograms of z1
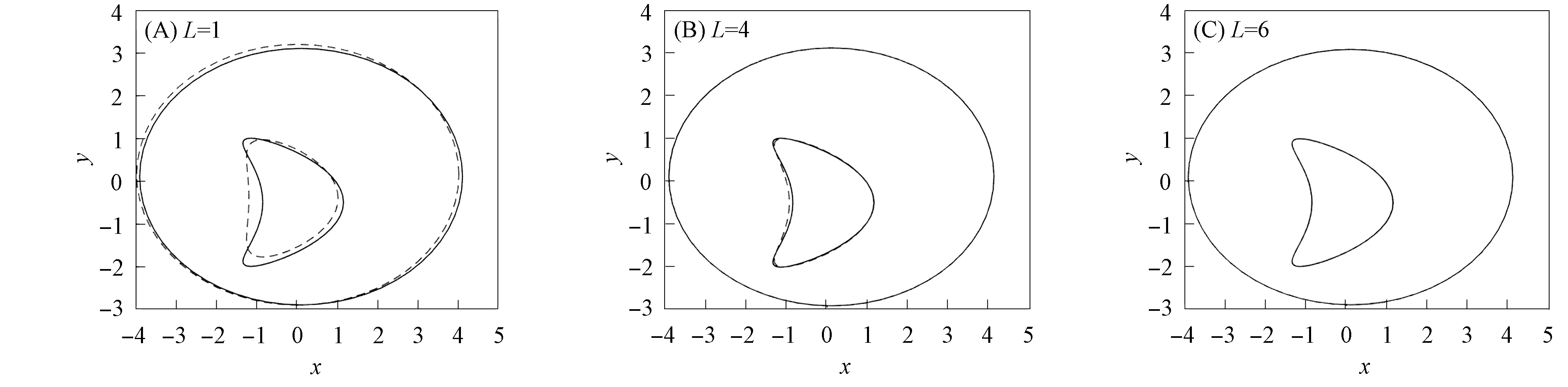
图3 入射波个数L=1时Γ0和Γ1的重构图Fig.3 Reconstruction diagrams of Γ0 and Γ1 when number of incident wave L=1
实验2考虑交界面Γ0为圆形三角形x(t)=(-0.1,-0.3)+(3+0.3cos 3t)(cost,sint), 嵌入障碍物边界Γ1为风筝x(t)=(-0.5+cost+0.65cos 2t,-0.5+1.5sint),n(x)=2.25, 波数k和k1分别为1和1.5, 入射波个数L=4, 观测孔径为[0,2π].参数Z可表示为
Z∶=(z1,z2,…,z14),
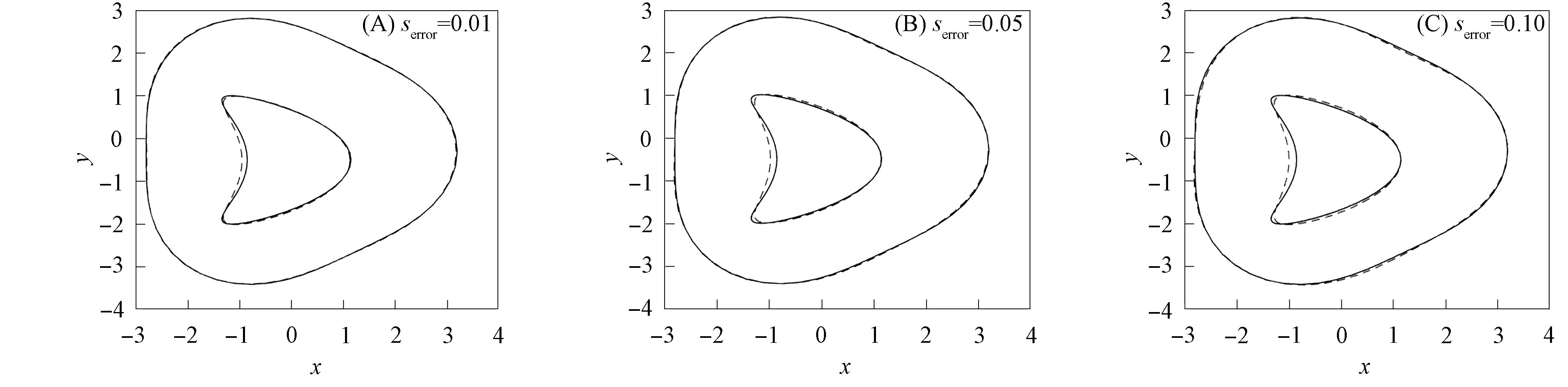
图4 入射波个数L=4时Γ0和Γ1的重构图Fig.4 Reconstruction diagrams of Γ0 and Γ1 when number of incident waves L=4
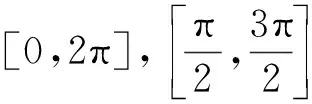

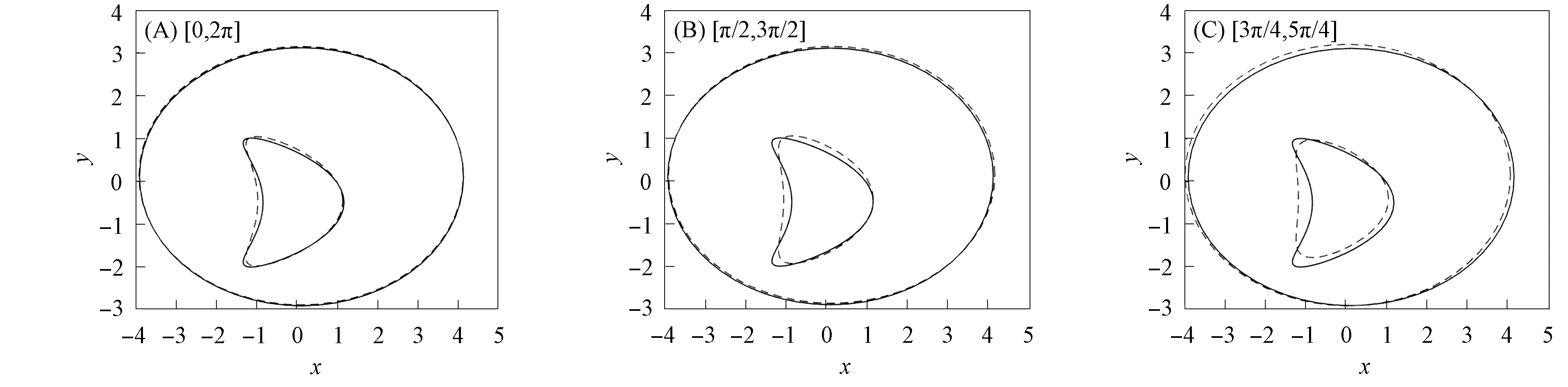
图5 入射波个数L=2时Γ0和Γ1的重构图Fig.5 Reconstruction diagrams of Γ0 and Γ1 when number of incident waves L=2
综上, 本文提出了同时重构非均匀介质以及嵌入声软障碍物的Bayes方法. 通过少量的入射波进行入射即可较好地重构出非均匀介质和嵌入声软障碍物. 数值实验结果表明, 所提Bayes方法可行且有效.
