Time sequential influence maximization algorithm based on neighbor node influence①

CHEN Jing (陈 晶), QI Ziyi∗, LIU Mingxin

(∗School of Information Science and Engineering, Yanshan University, Qinhuangdao 066004, P.R.China)(∗∗Hebei Key Laboratory of Virtual Technology and System Integration, Qinhuangdao 066004, P.R.China)

(∗∗∗Hebei Key Laboratory of Software Engineering, Qinhuangdao 066004, P.R.China)

(∗∗∗∗College of Electronic and Information Engineering,Guangdong Ocean University, Zhanjiang 524088, P.R.China)

Abstract In view of the forwarding microblogging, secondhand smoke, happiness, and many other phenomena in real life, the spread characteristic of the secondary neighbor nodes in this kind of phenomenon and network scheduling is extracted, and sequence influence maximization problem based on the influence of neighbor nodes is proposed in this paper. That is, in the time sequential social network, the propagation characteristics of the second-level neighbor nodes are considered emphatically, and k nodes are found to maximize the information propagation. Firstly, the propagation probability between nodes is calculated by the improved degree estimation algorithm. Secondly, the weighted cascade model (WCM) based on static social network is not suitable for temporal social network. Therefore, an improved weighted cascade model (IWCM) is proposed, and a second-level neighbors time sequential maximizing influence algorithm (STIM) is put forward based on node degree. It combines the consideration of neighbor nodes and the problem of overlap of influence scope between nodes,and makes it chronological. Finally,the experiment verifies that STIM algorithm has stronger practicability, superiority in influence range and running time compared with similar algorithms, and is able to solve the problem of maximizing the timing influence based on the influence of neighbor nodes.

Key words: neighbor node influence, time sequential social network, influence maximization(IM), information propagation model

0 Introduction

With the rapid development of Internet, more and more people like to spread their ideas and information through social media to influence other users on the platform. How to make the shared information spread quickly and influence the widest range has become a hot issue in the field of social network analysis.For this kind of problem,Ref.[1] proposed the influence maximization problem for the first time. At present, the widely used problem of influence maximization based on static social network is to findkusers in the social network as seed nodes, so that the information can influence other users in the network as much as possible throughkusers under a specific propagation model.

At present, most studies usually abstract social network as static graph, which simplifies the study of influence maximization problem, while neglecting some important characteristics existing in the actual network,thus causing the problem of inaccurate scope of influence. To solve this problem, in view of the timing of network and the propagation characteristics of neighbor nodes, taking the timing social network and secondlevel neighbor nodes as the research objects, and a timing influence maximization algorithm based on the influence of neighbor nodes and the improved weighted cascade model (IWCM) is proposed in this paper.This algorithm has strong pertinence and practicability,and can efficiently solve the problem of maximizing the time sequential influence based on the influence of neighbor nodes.

Because time sequential effect maximization research based on the influence of the neighbor node is very few, and most studies focused on only considering the temporal characteristics of the network or only considering the influence of the neighbor nodes, without considering a variety of characteristics of network, so the timing effect maximization problem based on the influence of the neighbor node challenges are as follows.(1) The traditional information dissemination model does not consider the timing characteristics of the network, it cannot be applied to the timing social network; (2) In the process of seed node selection, it is necessary to comprehensively consider the propagation characteristics of the second-level neighbor nodes and the timing of the network.

In order to solve the above problems, taking the time sequential social network as the research object,timing the traditional information transmission model,the time sequential influence maximization algorithm is designed based on the influence of neighbor nodes.Firstly, the influence measurement method of secondlevel neighbor nodes and the selection method of seed nodes are given. Secondly, the second-level neighbor node influence measurement method is time-serialized so that it can be applied to time-series social networks.Second-level neighbors time sequential maximizing influence algorithm (STIM) takes full account of various characteristics of the network, and is able to efficiently solve the problem of maximizing the time sequential influence based on the influence of neighbor nodes, and provides a foundation for the modeling of related problems, the selection of seed nodes and how to reduce the time complexity.

The major contributions of this paper are as follows.

(1) On the basis of the traditional weighted cascade propagation model, a new method of transmission probability between computing nodes is introduced,and an improved weighted cascade model is proposed.It enables information to be transmitted in the social network graph based on time sequential relationship.

(2) In view of the propagation characteristics of secondary neighbor nodes in the network, the influence measurement method of secondary neighbor nodes is designed, and the timing characteristics of the network are integrated into the selection process of seed nodes.

(3) It is verified that STIM algorithm can efficiently solve the problem of time sequential influence maximization based on the influence of neighbor nodes,and guarantee a high influence range under the premise of short running time.

The structure of this paper is as follows. In Section 1, the related work is introduced. In Section 2,the main definition and propagation model of the time sequential influence maximization problem based on the influence of neighbor nodes are discussed. In Section 3, the correlation algorithm of the time sequential influence maximization problem based on the influence of neighbor nodes is described. In Section 4, the experiment results on different data sets are analyzed and compared. In Section 5, the work of this paper is summarized and prospected.

1 Related work

In recent years, researchers at home and abroad have done a lot of research work on impact maximization. Kempe et al.[2]proposed the greedy algorithm for the problem of influence maximization (IM) and proved that its operation result could reach an approximate optimal of 63%. However, the greedy algorithm still has a high time complexity and is not suitable for large-scale social networks. Leskovec et al.[3]optimized the traditional greedy algorithm for the submodularity and monotonicity of the influence maximization problem, and proposed a cost-effective lazy-forward(CELF) algorithm, which is about hundreds of times faster than the greedy algorithm. Goyal et al.[4]proposed CELF ++ by optimizing CELF algorithm, and proved that it was 35% -55% faster than CELF.

All the above algorithms are greedy algorithms or improved greedy algorithms. In recent years, many researchers have studied heuristic algorithms with lower time complexity. Chen et al.[5]proposed the DegreeDiscount algorithm to solve the overlap problem of influence range of traditional degree estimation algorithms. The node with the highest degree is selected as the seed node, and then the degree of the neighbors of the selected node is discounted untilknodes are selected. Zhou and Gao[6]used PageRank algorithm to estimate the influence of nodes, and selected nodes with greater influence as alternative nodes to calculate the combined collision probability of alternative nodes. Li et al.[7]proposed an influence maximization algorithm based on k-kernel filtering in combination with the heuristic algorithm. It has been verified that the algorithm has a wider scope of influence compared with the existing heuristic algorithm.

At present, more and more researchers begin to study the extension deformation with maximum effect.Qiu et al.[8]proposed the influence maximization algorithm of overlapping communities, which could increase the running time by up to 90% and could be applied to large social networks. Ren et al.[9]proposed the problem of influence maximization under multi-topic consciousness. Across-social network model of influence maximization for topic perception is designed by improving the linear threshold model, and seed nodes are selected by means of heuristic algorithm. Li et al.[10]took price and other factors into consideration, and studied how to price a product under multiple conditions to maximize income. Zhao et al.[11]took into account the situation that there are multiple relationships among users in social networks and that multiple relationships affect information transmission together, MRRRSET algorithm was proposed to solve the problem of influence maximization of multi-relationship social networks.

Kim et al.[12]transferred the research object of maximum impact to the dynamic graph and designed an algorithm to deal with the update operation on the dynamic graph. Wang et al.[13]defined novel influence maximization (IM) queries in social networks and used a window sliding model to solve the problem of realtime impact maximization on dynamic graphs.Zhang et al.[14]studied the problem of influence maximization when there are different relationships in the network that mutually promote communication and inhibit communication. Guo and Lu[15]improved the sketch-based design influence maximization algorithm and applied it to the influence maximization problem of dynamic graphs, then recalculated the seed node set by calculating the influence of the deletion or addition of nodes on the current sampling set. Cao et al.[16]set a time window and regarded the connection between nodes as an action. The window slides down with time, and then the new action enters the window while the old action exits. According to the entry and exit of nodes, it is judged whether it is necessary to recalculate the seed nodes in the window obtained in the previous period to solve the problem of maximizing the influence in the dynamic graph. Wu et al.[17]studied the problem of influence maximization with the object of time sequence diagram, improved the traditional independent cascade model, and proposed two algorithms AIMT and IMIT to solve the problem of influence maximization of time sequence diagram. Wei et al.[18]studied the influence maximization problem of dynamic social networks with time change as the main feature, and proposed the influence maximization algorithm of dynamic social networks based on the feature. Yang et al.[19]proposed a method to measure the influence of complex network nodes with three levels of neighbors according to the propagation characteristics of neighbor nodes. This method regarded the neighbors of node level 2 and 3 with propagation attenuation characteristics as a whole to measure the influence ability of nodes.

2 Problem definition

2.1 Basic definition

Definition 1 (time sequential social network)Given networkGT(V,E,TE) based on the time sequential relationship between social network diagram,Vrepresents node set,Erepresents the edge of the collection, including |V| =n, |E| =m,TErepresents the set of moments with connection between nodes in the network, andT(u,v)represents the set of moments with connection between nodesuandv.

Take Fig.1 as an example to illustrate the social network graph based on time sequential relationship.Compared with static social network graphG(edge weights for the node transmission probability), time sequential social network graphGTare given the concept of timeline, each node only at specific time points, the weight on the edge represents the moment when there is a connection between the two nodes. For example, in Fig.1(b), nodeaand nodebare only connected at two moments 3 and 6, there is no connection at other moments. Now calculate the influence range of nodeain Fig.1(a) and Fig.1(b) respectively. The calculation process is as follows.

For convenience of calculation, it can be supposed that the propagation probability between nodes in Fig.1(a) and Fig.1(b) is the same, and is the weight values of each edge in Fig.1(a). Therefore, in Fig.1(a), nodeaactivates nodeband nodecwith probabilities of 0.1 and 0.03, respectively. If nodecis activated at this time, then nodecactivates nodeewithaprobability of 0.1. If nodeeis activated at this time, then nodeasuccessfully activates nodecande,with an influence range of 2. In Fig.1(b), nodeaactivates nodeband nodecat moments 3 and 2 with probabilities of 0.1 and 0.03, respectively. If nodecis activated, then nodecwill be activated after time 2.Since nodecand nodeeare only connected at time 1,and nodecis not activated at time 1, nodecwill no longer be able to activate nodee.Therefore, nodeawill only successfully activate nodecand its influence range is 1.

Therefore, it can be seen that if only the static graph-based influence maximization algorithm is applied to the time sequential social network graph, the correct result cannot be obtained. Therefore, it is necessary to study the time sequential relations based social network influence maximization problem.

2.2 Calculation of propagation probability

Definition 2 (propagation probability) The probability that the active nodeusuccessfully activates its neighbor nodevthrough the edge (u,v) is the propagation probability, expressed asPu,v∈[0,1].

Fig.1 Static graph and time sequential social network graph

In the traditional research of influence maximization algorithm, the degree estimation method is usually used to calculate the probability of inter-node propagation, that is, the reciprocal of in-degree of the node is used to estimate the probability of the node being activated by the upper node, as shown in Eq.(1).

Pu,v=1/InDegree(v) (1)

In Eq.(1), InDegree(v) represents the in-degree of nodev.

This method has been well proved and applied in the traditional research of influence maximization algorithm. However, the method does not take into account the problem of different contact times between nodes in the social network graph based on time sequential relationship. Now, an example is given to illustrate this problem, as shown in Fig.2. In the static graphG,the in-degree of nodecis 2, the probability that nodecis affected by both nodesaanddis 1/2. But in figureGT, when considering the number of connections, it can be found that the contact number of nodescandais less than the contact number of nodescandd, and the more times a node is contacted, the greater the probability that it will be affected. Therefore, in Fig.2(b), the probability of nodecbeing affected by nodeashould be less than the probability of nodecbeing affected by noded.The calculation result is inconsistent with that in Fig.2(a), that is, it is inaccurate to use traditional degree estimation methods to calculate the probability of node influence in a time sequential social network graph.Therefore,the traditional calculation method needs to be improved.

In the Eq.(2),|T(u,v)| represents the number of connections between nodeuand nodev,andvkrepresents all in-degree nodes of nodev.

Fig.2 Schematic diagram of propagation probability calculation

2.3 Improvement of weighted cascading model

2.3.1 Traditional weighted cascading model

In the traditional weighted cascade model(WCM),each directed edge(u,v) is given a real valuePu,v=1/InDegree(v) andPu,v∈[0,1], wherePu,vrepresents the probability that nodeusuccessfully influences nodevthrough the directed edge (u,v).The propagation process of WCM model is as follows: at the initial timet,the active nodeuhas only one chance to activate each of its inactive neighbor nodesv,and the activation probability isPu,v.If nodevhas multiple active parents at timet,then the active parent node activates nodevin any order at timet.Ifvis successfully activated, it becomes active node at timet+ 1 and tries to activate its next level of inactive neighbor node in the same way. This cycle continues until no new nodes in the network are activated.

2.3.2 Improve the weighted cascade model

Definition 3 (node active initial time) The time when nodevis successfully activated by its active parent nodeuis its active initial time, which is expressed asActvandActv=min{t|(t∈T(u,v) andt≥Actu)}.

Take Fig.2(b) as an example, the set nodedis the seed node (the initial active time of the seed node is 0),and if it successfully activates nodec,Actc=min{4,5} =4.

The traditional influence maximization algorithm does not consider the initial time when nodes are activated,while the initial time when nodes are successfully activated in the time sequential social network graph needs to be considered. Therefore, the traditional weighted cascade model is improved, and a new propagation model is obtained based on time sequential social network graph—improved weighted cascade model in this paper.

Take Fig.1(b) as an example, let nodedbe the seed node and successfully activate its neighbor nodec,then the initial active time of nodec,Actc=2, that is, nodecis active after time 2. And because nodecand nodeeare only connected at time 1, at this timecis still in an inactive state, so nodecmust not activate nodee.

The IWCM propagation model is proposed based on the WCM propagation model, so that information can be transmitted in the social network graph based on the time sequential relationship. The propagation process of information in the time sequential social network diagram through the IWCM model is described as follows.

(1) In the initial network, the initial active time of all nodes is set toActv= - 1, indicating that all nodes are in an inactive state. Set the initial active time of seed nodeu,Actu=0, indicating that the seed node is in active state at the time of 0. At this point,seed nodeuactivates its neighbor nodevwith a certain probability, and nodeuhas only one chance to try to activate nodev.

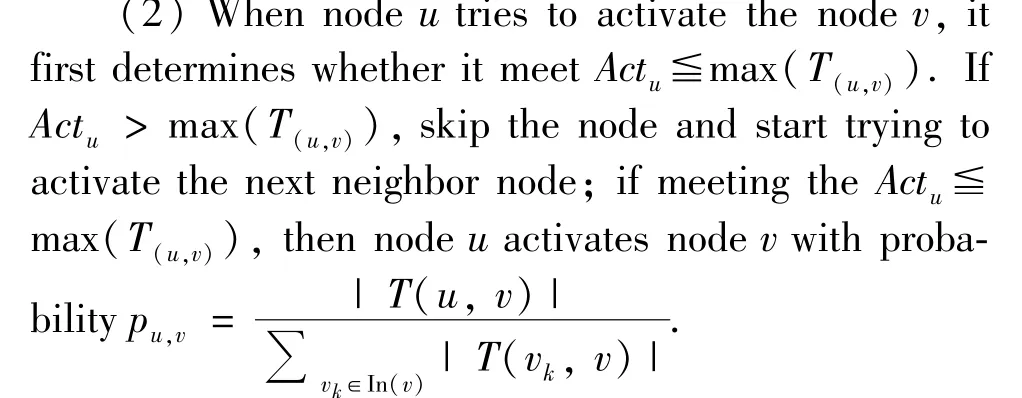
(3) No matter whether the node can activate nodevor not,uwill not try to activate nodevin the future propagation process.

(4) If nodevis successfully activated, its initial active timeActvis recorded, whereActv∈T(u,v),Actu≦Actv≦max(T(u,v)).

(5) In the whole network, information is transmitted from new active nodes to inactive neighbor nodes until no new nodes in the network are activated.

2.4 Problem definition

This section defines and explains the problem of time sequential influence maximizing based on the description of the above discussions. And the concept of node influence and marginal benefit in time sequential social network is introduced.

Definition 4 (node influence) Node influence refers to the set of all nodes that can be successfully activated by nodevin the network, expressed asσ(v).

Definition 5 (marginal benefit) The marginal benefit of nodevrefers to the increase in revenue that can be brought by adding a nodevto the seed setS.The calculation formula is shown in Eq.(3).

Problem definition (time sequential influence maximization problem based on neighbor node influence) Given time sequential social network graphGT= (V,E,TE), and specific propagation model, in the time sequential social network to find a node setS,the number of nodes in the setS|S|=k, make the effect of the setSmost widely, setSis the seed node set ofGT.

3 Time sequential influence maximization algorithm based on neighbor node influence

3.1 Influence measurement method of second-level neighbor nodes

The influence of nodes on second-order neighbor nodes can be explained by independent probability events in probability statistics. Independent probabilistic events are defined as:if eventAand eventBare independent,thenP(AB)=P(A)×P(B),that is,the probability of eventAand eventBoccurring at the same time is the probability of eventAmultiplied by the probability of eventBoccurring.

Similarly, in the time sequential social network as shown in Fig.3, the probability that node 1 activates node 4 through node 2 is the probability that node 1 activates node 2 multiplied the probability that node 2 activates node 4 , that is,P(node1activatesnode4throughnode2)=0.2 ×0.3 =0.06.

Fig.3 Social network diagram (second-level neighbor)

Given the time sequential social networkGT(V,E,TE),VandErepresent network node set and edge set respectively, andTErepresents the set at the time when there is a connection between nodes.According to the improved weighted cascading model, the probability that nodeuactivates its neighbor nodevisPu,v,and the probability that nodevactivates its next-level nodev1isPv,v1,then the probability that nodeuactivates its neighbor node and second-level neighbor node along the path (u,v,v1) is shown in Eq.(4).

P=Pu,v+Pu,v×Pv,v1(4)wherein,Prepresents the sum of the probability that nodeuactivates its neighbor nodes and second-level neighbor nodes on the path (u,v,v1).

Therefore, nodeuis the sum of activation probabilities of all its neighbor nodes and second-level neighbor nodes in the whole network, as shown in Eq.(5).

Since the influence range of nodes is directly affected by the activation probability between nodes,Eq.(5) can be used to estimate the influence range of nodes. However, when information is transmitted in the actual social network as shown in Fig.3, node 3 is set as the seed node, and the information transmission process is as follows.

Time step 0 Activate node 3.

Time step 1 Node 3 tries to activate node 2 and node 1 with probabilities of 0.15 and 0.2 respectively,assuming that both node 2 and node 1 are successfully activated.

Time step 2 Since node 2 is already active at this time, node 1 will not try to activate node 2 again.However, when calculating the influenceP1of node 1,the influence probability of node 1 on node 2 has been included, which is inconsistent with the actual transmission process.

Considering the influence range overlap between the nodes, when nodeiis selected as seed nodes, all parent nodesuand ancestor nodesv(the relationship between nodei, nodeu, and nodevare shown in Fig.4) are treated with influence discount. In its estimate, subtract the overlapping part of influence, as shown in Eqs(6) and (7).

wherein, nodevis the ancestor node of nodei, and nodeuis the parent node of nodei.

Fig.4 Schematic diagram of node relationship

3.2 Timing of influence

Due to the addition of time sequential relationship in time sequential social network, Eqs(6) and (7)need to be time-serialized.As shown in Fig.5, assuming that the initial active time of node 4 is 2, node 4 is already active when node 4 contacts node 2 and node 5. Therefore, node 2 and node 5 have a chance to be activated by node 4 respectively. However, if the initial active time of node 4 is assumed to be 5, node 4 is inactive in the two moments (2 and 3) when node 2 and node 4 are connected, so node 4 has no opportunity to activate node 2. But, node 4 is already active at the time 6 when node 4 is in contact with node 5.Therefore, node 5 has a chance to be activated by node 4 once. It can be seen that, since the initial active time of all nodes in the network is in an unknown state, the larger the maximum value of the contact time between two nodes, the greater the chance that the node has to be tried to activate.From the above examples, it can be seen that the maximum value of the contact time between two nodes max(T(u,v)) will have an impact on the influence range of nodes, and the larger the maximum value of the contact time between two nodes, the wider the influence range of nodes. Therefore, consideration of max(T(u,v)) is added into the estimation formula of the influence range of nodes, and the time-serialized formula is

Fig.5 Time sequential social network (second-level neighbor)

where,Pv′is the estimated value of influence of nodeuafter discount.

At the same time, the influence of its ancestor nodevis updated, and the influence range of the updated node is shown in Eq.(10).

3.3 Description of STIM algorithm

The main research strategy of STIM algorithm proposed is heuristic strategy, that is, the influence of non-seed nodes is estimated in each seed node selection process, and the nodeuwith the largest estimated value is selected as the seed node.

The idea of STIM algorithm is as follows: the problem of time sequential social network influence maximization is solved in two steps. Firstly, the node influence of the second-level neighbor is estimated according to the measurement method in subsection 3.1.Then, according to the influence estimation results,the nodeuwith the largest estimated value is selected as the next seed node, until allkseed nodes are found out. The specific description process of STIM algorithm is Algorithm 1.

Algorithm 1 STIM Input: social network GT(V,E,TE), k;Output: seed set S;(1) Calculate propagation probability between nodes in time sequential social network according to the calculation method of propagation probability between nodes in subsection 3.2;(2) Use Eq.(5) to calculate the influence of all nodes in the network, and make it time sequenced;(3) Select the node v with the greatest influence as the first seed node, mark node v as active state and add it to S;(4) Update the influence estimate of parent node of S and its grandfather node according to Eqs(9) and (10);(5) Select the node u with the largest influence estimation after updating as the second seed node and add it to S;(6) Repeat Steps (3) to (5) until k nodes are selected.

3.4 Pseudo code

GT(V,E,TE) is used to represent a social network based on time sequential relationship, whereVrepresents the set of nodes,Erepresents the set of edges,TErepresents the set of contact moments between nodes,krepresents the number of seed nodes required, andSrepresents the set of seed nodes. The pseudo code of the STIM algorithm is Algorithm 2.

Algorithm 2 Time sequential influence maximization algorithm based on neighbor node influence Input: social network GT(V,E,TE),k;Output: seed set S;(1) Initialize S =Ø;(2) For any node u in graph GT do;(3) Calculate Pu,v; //v indicates the next-level neighbor node of node u;(4) End for;(5) For any node u in graph GT do;(6) Pu′ = Pu - Pu,i × max(T(u,i) - ∑i1∈O(i)Pu,iPi,i1 ×min(max(T(u,i), max(T(i, i1)));(7) End for;(8) For i = 1 to k do;(9) v = argmaxu{Pu′| u ∈V/S};(10) S = S ∪{v};(11) End for.

In Algorithm 2,Step (1) initializes the seed setSto an empty set; In Steps (2) -(4), the propagation probability between nodes in time sequential social network is obtained based on in subsection 2. 2; Steps(5) -(7) estimate the influence range of all nodes;Steps (8) -(11) find the firstknodes with a larger estimated influence range and incorporate them into the seed set.

The time complexity analysis of STIM algorithm is as follows: let the number of nodes of networkGT(V,E,TE) ben, the number of edges bem, the size of seed set bek,and the number of contact moments between nodes in the network bet.In Algorithm 1, Steps(2) -(4), the time complexity generated when calculating the propagation probability between nodes isO(m);Steps (5) -(7) estimate the influence scope of each node in the time sequential social network, and the time complexity generated isO(n); Steps (8) -(11) selectknodes with the greatest influence and iteratekrounds, so the time complexity isO(k); To sum up, the time complexity of STIM algorithm isO(n+m+k).Since the value ofkis generally less than or equal to 50, that is, far less thannandm, soO(k)can be ignored, then the time complexity of the STIM algorithm isO(n+m).

4 Experiment and result analysis

Three real datasets of different scales are selected as input data to realize seed node selection and seed influence calculation in time sequential social network graph based on neighbor node influencein.

4.1 Experimental data and parameter setting

Dataset 1 used in the experiment is derived from the online social network of University of California,composed of private messages. Edges (u,v,t) indicate that userusends a private message to uservat timet[20].Dataset 2 is the E-mail data of a large European research institution, and the directed edges (u,v,t)indicate that userucommunicates with uservthrough E-mail at timet[21].Dataset 3 is a time sequential network that edits each other’s ‘conversation’ pages on behalf of Wikipedia users. Edges (u,v,t) indicate that useruhas edited the conversation page of uservat timet[22].The number of experimental datasets is shown in Table 1.

Table 1 Adoption number of experimental datasets

In this paper, the STIM algorithm is divided into two steps. The first step is to calculate the propagation probability between all nodes. The second step is to estimate the influence range of all nodes and selectknodes with the largest influence range as the seed node set. While realizing the algorithm, some classical algorithms and new algorithms in recent years with better running effect are reproduced. The advantages and disadvantages of each algorithm are compared and analyzed from two aspects of the influence range and running time of the algorithm.

Coverage threshold maximum influence (CTMD)is a degree maximum heuristic algorithm based on coverage threshold. This algorithm uses the improved kshell algorithm to calculate the influence of nodes in the network and select the initial seed node set. Meanwhile, the activation probability of nodes within two degrees is considered.

Influence estimation influence ranking (IEIR) is an algorithm based on influence estimation and influence ranking, and it has good comprehensive ability among traditional influence maximization algorithms at present.

DegreeDiscount is the representative of the heuristic algorithm. The node with the highest degree is selected as the seed node, and then the degree of the neighbors of the selected node is discounted untilknodes are selected.

Random, as a benchmark comparison method,simply randomly selectsknon-repeating nodes from the time sequential social network graph as seed nodes.

In the stage of seed node selection, CTMD algorithm, IEIR algorithm, DegreeDiscount algorithm,Random algorithm and STIM algorithm select the size of seed node setkas 5,10,15,20,25,30,35,40,45, and 50 respectively.

4.2 Influence of seed nodes in different algorithms

The correlation algorithm is tested on three different datasets. Scope of influence refers to the number of nodes ultimately affected by calculating the seed set through the algorithm in the initial stage of the network to spread the seed set in the network. The wider the influence range of the seed set,the higher the accuracy of the algorithm.

Fig.6 shows the seed nodes impact on the Wiki-Talk dataset.As can be seen from Fig.6, among many comparison algorithms, IEIR algorithm and STIM algorithm have a wide influence range, while the influence range of other algorithms is at a low level. When selecting different number of seed nodes, with the increase of the number of seed nodes,the influence range of IEIR algorithm is always in a stable state. As the number of selected seed nodes increases,the influence range of STIM algorithm expands. That is, when the number of seed nodes is less than 25, the influence range of IEIR algorithm is higher than that of STIM algorithm; but when the number of seed nodes is greater than 25, the influence range of STIM algorithm is higher than that of IEIR algorithm.

Fig.6 Effect of seed nodes on Wiki-Talk dataset

Fig.7 is an effect diagram of seed nodes on CollegeMsg dataset. It can be seen from Fig.7 that the influence range of STIM algorithm is much higher than that of other algorithms regardless of the size of the seed node set. Atk= 50,the influence range of STIM algorithm is 7.82 times,4.56 times,2.25 times, and 6.92 times that of IEIR algorithm, CTMD algorithm,DegreeeDiscount algorithm, and Random algorithm respectively. Among other algorithms, DegreeeDiscount algorithm has better effect, while IEIR algorithm, CTMD algorithm, and Random algorithm have worse effect.

Fig.7 Effect of seed nodes on CollegeMsg dataset

Fig.8 is an effect diagram of seed nodes on Email-Eu-Core dataset. As can be seen from Fig.8, STIM algorithm has the widest influence range, followed by IEIR algorithm and DegreeDiscount algorithm, and CTIM algorithm and Random algorithm have the smallest influence range. Whenk ＜15, the influence range of IEIR algorithm is higher than DegreeDiscount algorithm, while whenk ＞15,IEIR algorithm is overtaken by DegreeDiscount algorithm. Whenk= 15,the influence ranges of CTMD algorithm and Random algorithm reach the same level.

Fig.8 Effect of seed nodes on Email-Eu-Core dataset

4.3 Selection time of seed nodes in different algorithms

In this subsection, under the IWCM propagation model, the running time of CTMD algorithm, IEIR algorithm, DedegreeDiscount algorithm, Random algorithm, and STIM algorithm are respectively counted.The calculated time is the running time of 50 seed nodes selected from three datasets of different scales,as shown in Table 2.

Table 2 Running time of STIM algorithm

As can be seen from Table 2, the running time of STIM algorithm, CTMD algorithm, DedegreeDiscount algorithm, IEIR algorithm, and Random algorithm grows gradually with the gradual increase of the scale of time sequential social network. IEIR algorithm has the longest running time, followed by STIM algorithm, and other algorithms have relatively short running time.

The analysis of the experimental results shows that the Random algorithm has the shortest running time because of the randomness of seed node selection, but its influence range is much smaller than other algorithms.IEIR algorithm is a traditional influence maximization algorithm with better comprehensive ability. Although its influence range is relatively large, its running time is also the longest. CTMD algorithm is a relatively new influence maximization algorithm in the past two years.Although its running time is short, it does not consider the factors of time sequential and second-level neighbor nodes, which leads to the shrinkage of the influence range. DegreeDiscount algorithm is a heuristic algorithm that only considers first-level neighbor nodes.Compared with STIM algorithm, the running time of DegreeDiscount algorithm is smaller than that of STIM algorithm because the scope of neighbors it considers is smaller, but its influence scope is also much smaller than that of STIM algorithm.

5 Conclusion

In recent years, social phenomena such as secondhand smoke, happiness transmission and microblog forwarding have two main characteristics: (1) Time sequential change. As time goes on, the topology of such networks also changes constantly; (2) Secondary dissemination of information. Information is spread widely in the category of secondary neighbors in such networks. In view of the two characteristics of the network, the STIM algorithm is proposed in this paper.Firstly, the propagation probability between nodes is calculated by the improved degree estimation algorithm;Secondly,the traditional weighted cascade model is improved so that it can be applied to social networks based on time sequential relationships; Finally,STIM algorithm is proposed based on the improved weighted cascade model. Experimental results show that STIM algorithm is more targeted than CTMD, DedegreeDiscount, IEIR, Random and other influential maximization algorithms with universal characteristics.In the three networks selected in this section with time sequential characteristics and next-level transmission characteristics of information, STIM algorithm shows its advantages in terms of influence scope and running time, and can better solve the problem of maximizing the influence of next-level neighbor’s time sequential social network.

The following in-depth studies will be carried out in the future work: (1) Research the actual factors of the time sequential influence maximization problem based on the influence of neighbor nodes, such as the different information types, cost, time; (2) Expand the algorithm so that it can be applied to time sequential social networks targeting multi-level neighbor nodes.