A multispectral image compression and encryption algorithm based on tensor decomposition and chaos①

XU Dongdong(徐冬冬), DU Limin

(Electronic Information Engineering College, Changchun University, Changchun 130022, P.R.China)

Abstract A multispectral image compression and encryption algorithm that combines Karhunen-Loeve(KL) transform,tensor decomposition and chaos is proposed for solving the security problem of multi-spectral image compression and transmission. Firstly, in order to eliminate residual spatial redundancy and most of the spectral redundancy, the image is performed by KL transform. Secondly,to further eliminate spatial redundancy and reduce block effects in the compression process, two-dimensional discrete 9/7 wavelet transform is performed, and then Arnold transform and encryption processing on the transformed coefficients are performed. Subsequently, the tensor is decomposed to keep its intrinsic structure intact and eliminate residual space redundancy. Finally,differential pulse filters are used to encode the coefficients,and Tent mapping is used to implement confusion diffusion encryption on the code stream. The experimental results show that the method has high signal-tonoise ratio,fast calculation speed,and large key space,and it is sensitive to keys and plaintexts with a positive effect in spectrum assurance at the same time.

Key words: Karhunen-Loeve (KL) transform, tensor decomposition, differential pulse filter,Tent map

0 Introduction

Remote sensing is a comprehensive detection technology based on aerial photography and interpretation[1]. Due to its wide coverage, strong detection capabilities, and comprehensive data acquisition, it has been used for decades on reconnaissance, meteorological observation, and resource census. Multispectral imaging systems as an important part of satellites are developing towards high resolution and large field of view. It gets more detailed and accurate information to improve the recognition ability of ground and ocean targets with high resolution;and it also makes the coverage of the space camera larger and effectively improves the work efficiency. With the increase in resolution and field of view, the amount of data output by the space camera becomes larger and larger, which puts forward higher requirements on the compression and decompression algorithms of related images. In addition, it is necessary to encrypt multispectral images to ensure data security.

For two-dimensional images and multispectral images, many compression encryption algorithms have been proposed. Ref.[2] proposed a 3D chaotic encryption scheme for compressed image. First, the set partitioning in hierarchical trees (SPIHT) encoding algorithm is used to compress the image, and then the images are mapped to a three-dimensional bit matrix.Next Lorenz is used to generate a chaotic sequence,and a series of processing is performed on the generated three-dimensional bit matrix. Finally the compressed and encrypted image is got. The method has a positive encryption effect, but the amount of data is huge. Ref.[3] proposed a hyper-spectral image compression algorithm based on adaptive spectrum recombination. It has a small amount of encrypted data but lacks security. Ref.[4] proposed an algorithm of joint hyperspectral image compression and encryption based on optimal spectrum prediction of inter-band, SPIHT and chaos mapping. It has a better compression efficiency and encryption effect, but the compression efficiency and key space need further improvement. Ref.[5]proposed a joint image compression-encryption scheme using entropy coding and compressive sensing, which has a better compression and encryption performance.

The compression encryption algorithm mentioned above are aimed at two-dimensional images, with little research on multispectral images. Different from ordinary two-dimensional images, multispectral images contain hundreds of continuous spectrum imaging information with spatial and spectral dimensions. The amount of data is huge, which makes the subsequent processing of multispectral images more complicated.Considering the characteristics of multispectral images and referring to the latest Karhunen-Loeve (KL) transform technology[6-7], this paper proposes a multispectral image compression encryption algorithm based on chaos and fast wavelet transform, which closely combines the compression process with the encryption process together. While improving the efficiency of image storage and transmission, the security of the image is guaranteed, and higher compression efficiency and better encryption effect are achieved.

1 KL transformation

KL transformation (KLT) can be used in principal component analysis (PCA). It is a linear and reversible transform with decorrelation performance. The calculation process of the original algorithm is as follows.

First, the multispectral image matrix containingNspectral bands is integrated into a two-dimensional matrixYusing the row stacking method, and the average value of the vectorYis calculated. The process of calculation is shown in Eq.(1).

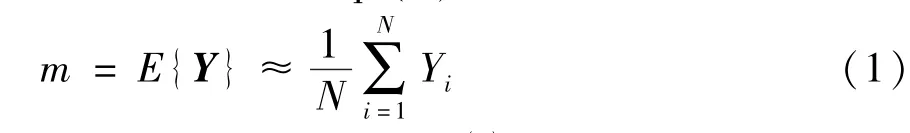
Secondly, the covariance matrixCof the vectorYis calculated, and the calculation process is shown in Eq.(2).

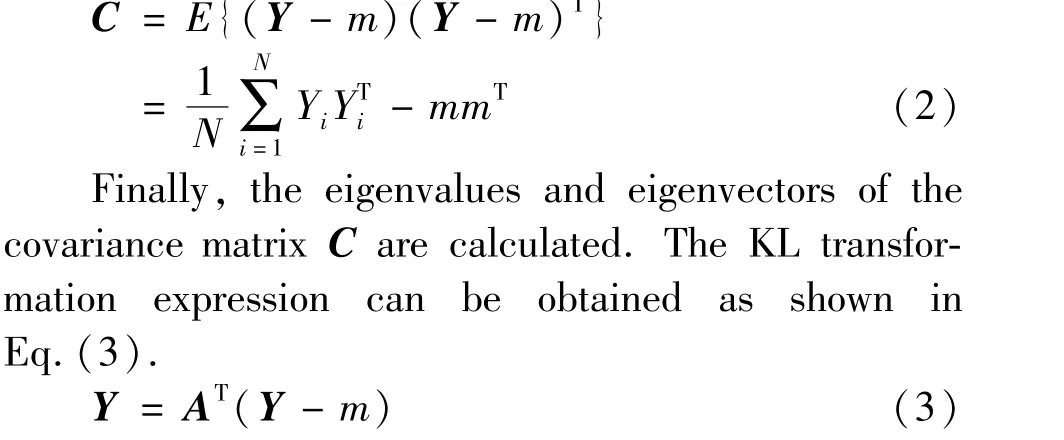
wheremis the mean ofY,E{} represents the mean of the vector.

whereAis the eigenvector ofC.The algorithm requires a huge amount of calculations, among which the calculation of theM×Nsize spectrum requires(M×N-1) times additions and one division,and the calculation of normalization of the data requires(M×N)times subtractions.Other operations require higher computational complexity. Therefore, the following improvements will be made to solve this problem.

First of all, when the covariance is calculated, a subset of the spectral vectors is randomly selected instead of using all the spectral vectors, and the size of the subset is appropriately selected to minimize the computational complexity while ensuring image quality.The effect of sampled size on compression performance is shown in Fig.1. From Fig.1 it can be seen when the sample size is 1/1000 of the traditional method, the compression performance starts to decline, and the calculation complexity is also low. The value is selected as the sampling ratio to estimate the covariance considering the compression performance and calculation time.

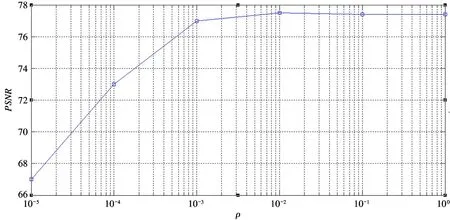
Fig.1 The effect of sampling ratio on compression performance

Table 1 shows the comparison of the KLT execution time of the 512 ×512 ×4 image using the downsampling method. It can be seen that under the premise of ensuring certain compression performance, the calculation time of this method is greatly reduced.

Table 1 Calculation time comparison

The Jacobi algorithm is often used to find the eigenvalues and eigenvectors of the symmetric matrix.However, the algorithm requires not only the main element, but also the row and column rotation transformation to obtain the eigenvalues at the same time, which makes the whole calculation process very complex and difficult to implement in parallel.

Finally, the eigenvector matrix is calculated using a lifting scheme instead of matrix multiplication (mean×eigenvector) in classic KLT. The eigenvector matrix is decomposed intoAT=PLUS, wherePis the permutation matrix,Lis the unit lower triangular matrix,Uis the unit upper triangular matrix, andSis the diagonal matrix. The output elements are rounded after each stage to maintain no floating point output. The improved KL expression is shown in Eq.(4).

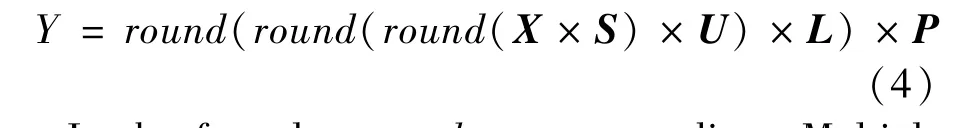
In the formula,roundmeans rounding. Multiplying byPis the element swap, where the multiplication is only performed by 1 and 0. The permutation is not computationally intensive, because it only needs to loop through the vector to exchange certain elements.TheSmatrix is a sparse lower triangular matrix,and therefore fewer element multiplication operations can be required by applying the zero check technique to the multiplication operation.

The transformed effect diagram is shown in Fig.2.KLT is performed on the upper three spectral bands(a, b, c) of a multi-spectral image (including 4 spectral bands) respectively to obtain three transformed images (d, e, f), which eliminate most of the interspectral redundancy, and the energy is mainly concentrated in the first two spectral bands.

Fig.2 KL transformation effect diagram of each spectrum

2 Wavelet encryption algorithm

The encryption algorithm is composed of three parts: subkey generation, wavelet coefficient scrambling and data stream encryption.

2.1 Subkey generation

The chaotic system is improved Logistic mapping and Tent mapping, the improved mapping equation is

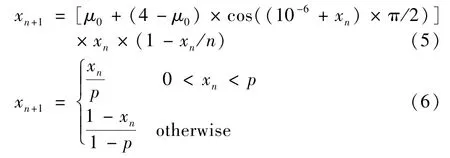
wherep∈(0,1),xn∈[0,1],μ0is 3.569945673,and 1/n∈(0,1) is the amplification factor. Whenμ∈(3.569945673,4], the sequence generated by Logistic mapping is in a chaotic state. When its value is 4, the system is in the best chaotic state, but the encryption effect is poor at this time. In order to solve the problem of poor encryption effect when value is 4, an infinite approach expression of 4 is adopted to replace 4 to achieve the expected chaotic characteristics and safety.

The output hash values are divided into 5 groups,denoted asf1,f2,f3,f4,andf5.The sub-key is generated by Eq.(7) as the initial value of Logistic mapping.

2.2 Scrambling of wavelet coefficients

After the general pixel is constructed, it is necessary to perform wavelet transformation on the pixel to reduce the blocking effect in the compression process and protect the real information of the image. Wavelet transform is a new transform method proposed on the basis of Fourier transform. While continuing the localized advantage of short-time Fourier transform, it overcomes a series of shortcomings of Fourier transform. The two-dimensional discrete wavelet transform can be obtained by Eq.(9).

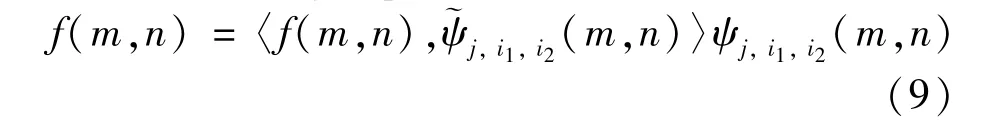
After performing a wavelet transform on the image, four subbands, namely low frequency subband(LL), horizontal high frequency subband (LH), vertical high frequency subband (HL), and diagonal high frequency subband (HH) will be generated. The secondary transformation is to repeat a similar division on the basis of the LL. Better research results will be achieved by processing differently for different subband coefficients.

In this paper, Arnold transform is used to scramble the coefficients after wavelet transform. According to the Arnold transform periodic table, the appropriate number of scrambling times are selected to transform and scramble the target pixel to obtain a transform scrambling map.

2.3 Tensor decompositon

In order to optimize the above formula, many methods have been proposed mathematically. Among them, the dGN algorithm is derived from the Newton method. However,due to the relatively large amount of calculation and difficulty in implementation, it has not been used in multi-spectral image processing. The algorithm has low complexity and fast convergence speed,making it more suitable for multi-spectral image compression through appropriate improvements.

Through the following formula, the dGN iterate can be got.

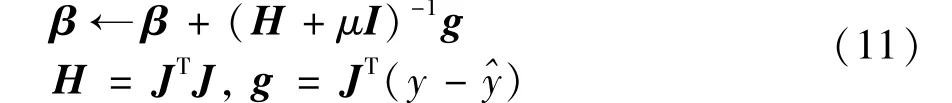
Among them,β= [vec(A(1))T, vec(A(2))T,vec(A(3))T],Iis the identity matrix,His the Hessian matrix,μis the damping parameter,gis the gradient,^y= vec(^Y),y= vec(Y),andJis the Jacobian matrix.

The huge amount of calculation required for the iterative process mainly comes from the calculation ofHandg. In order to speed up the calculation, this paper improves the calculation of the Hessian matrixHand the gradientgrespectively. Suppose the symbols of Kronecker product, Khatri-Rao product, and Hadamard product are ⊗, ☉ and Θ, respectively,Eq.(12) is defined as

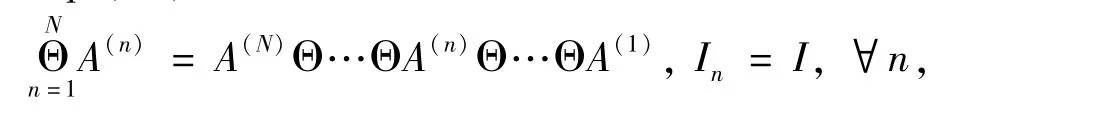
Eq.(19) still requires a large amount of calculation. The main calculation amount is concentrated on the calculation of the Jacobian matrixJand the creation of the matrixLμ. This article will further simplify the three main parts of the iterative Eq.(19), the simplification process is shown in Eq.(20) and Eq.(21)respectively.

The norm is a reinforced concept of distance, andlPnorm is not a norm, but a set of norms.l1norm can lead to a sparse solution. And it can produce a more sparse model thanl2norm, andl1norm can be used to feature selection.

The above formula uses thel2norm, which is not suitable for image compression, so we change it to thel1norm , and the new iteration rule is as in Eq.(22).

Fig.3 is a performance comparison chart between the algorithm and other three algorithms. It can be seen from Fig.3 that compared with the hierarchical alternating least squares (HALS) and the least squares(LS), the algorithm proposed in this paper has the advantage of fast convergence; compared with the original dGN algorithm, although the convergence speed is slightly slower, the calculation amount of this system is much smaller than the latter, and the improved algorithm is more suitable for multi-spectral image compression.

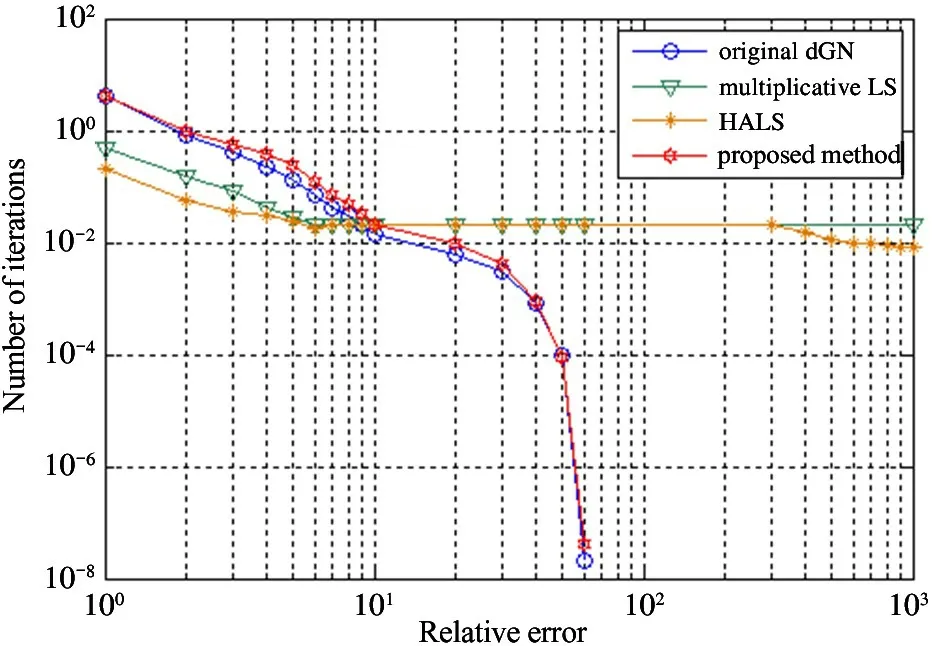
Fig.3 Convergence speed comparison of decomposed three-dimensional tensor

2.4 Data stream encryption

For further compression, the original signal needs to be converted into a new integer stream. Then the integer stream is converted into a binary coded stream,and Huffman coding is adopted. However, if these integers are directly converted into a binary bit stream through Huffman coding, too much storage space will be required. Therefore, the differential pulse code modulation (DPCM) filter is used to convert the original signal into a new integer array.

Firstly, the non-zero coefficients are uniformly quantized with a quantizer. The original signal is converted into a new integer array to save storage space and further compress the non-zero coefficients. Finally, the integer stream is converted into a binary coded stream to achieve efficient image coding.

3 Experimental results

3.1 Encryption performance analysis

The algorithm has 5 initial keys in total, and the precision space generated by each key is close to 1016.During the encryption process, the key changes continuously as the plaintext changes. Therefore, it has a larger key space and known plaintext attacks and brute force attacks can be effectively resisted.

In order to verify the sensitivity of the algorithm to the key, the original image is encrypted with a key of a slight difference, and the rate of change of the code stream is compared. It can be obtained through experiments that the output bit stream change rate remains between 47.62% -47.72%, which has good key sensitivity.

With the key unchanged and the value of a certain pixel in the image being randomly changed, the sensitivity of this algorithm to plaintext is evaluated through the encrypted bit stream change. 100 simulation experiments on QuickBird with different characteristics and specific compression ratios are performed. The experiment shows that the ciphertext bit stream change rate remains at 47. 45% -47. 53%. It can be seen that this algorithm is very sensitive to plaintext images and the differential attacks can be effectively resisted.

The number of pixels change rate (NPCR) and the unified average changing intensity (UACI) are important indicators for effective analysis of resistance to differential attacks. Among them,NPCR represents the ratio of different gray values of different ciphertext images at the same position, and UACI represents the average change density between different ciphertext images. Table 2 lists the NPCR and UACI test results of this algorithm and several other algorithms.

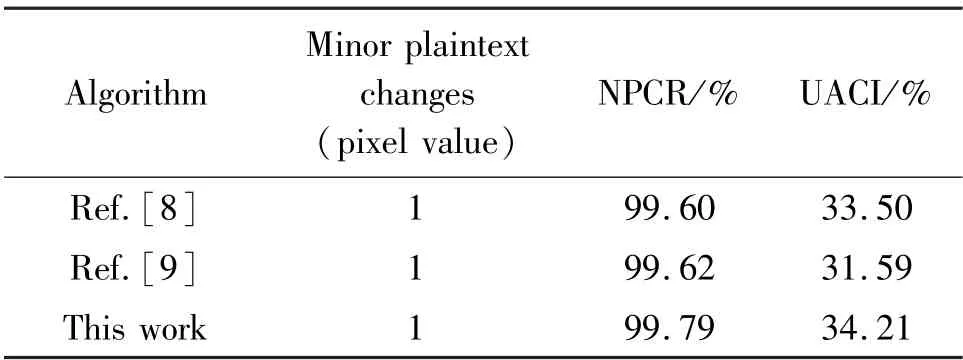
Table 2 Test results of NPCR and UACI

The higher the values of NPCR and UACI, the better the encryption effect. It can be seen from Table 2 that the NPCR and UACI of this algorithm are closer to ideal values. Therefore, compared with similar algorithms, this algorithm can better resist differential attacks.

3.2 Compression performance analysis

A multispectral image with three spectral bands is selected as the test image to verify the feasibility of the algorithm. The whole algorithm is simulated on the computer. The pixel depth is 8 bit/pixel(b/p), and the compression ratio is 16∶1. The experimental results are shown in Fig.4.

It can be seen from Fig.4 that when the bit rate is relatively high, the PSNR is particularly high, and the reconstructed image is not much different from the original image. After DWT and KLT has been performed on images,most of the pixel values are located in 1 bit,the spectral redundancy is eliminated.

Fig.4 Comparison of original image and compressed reconstructed image

To verify the quality of the compressed image further,4 groups of QuickBird multispectral images with different characteristics were selected for testing. And the recently proposed multispectral image compression algorithm is used for comparison. The comparison results are shown in Table 3.

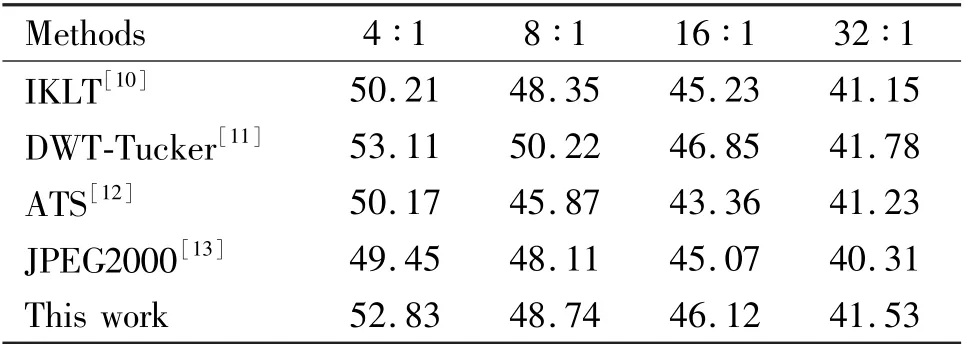
Table 3 Compression system test results

It can be seen from Table 3, within the compression ratio range of 4 ∶1 -32 ∶1,the proposed algorithm achieves a high peak signal-to-noise ratio, which is superior to many existing compression algorithms. Also,this algorithm is feasible and particularly suitable for the occasions of higher compression ratio.

Table 4 shows the data processing speed of this algorithm compared with some existing algorithms. It can be seen from Table 4 that the data throughput rate of the compression algorithm proposed in this paper is lower than the existing compression algorithm, and the processing speed is equivalent to JPEG 2000, but the compression ratio is much higher than JPEG 2000 and other compression algorithms. Compared with other compression algorithms,one reason for the slightly lower throughput rate of this algorithm is that the encryption algorithm is added to the algorithm, which increases the complexity of the algorithm. As the hardware improves, the processing speed of the algorithm will continue to increase, and the advantage of the algorithm, namely high peak signal-to-noise ratio, will become more obvious at the same time.

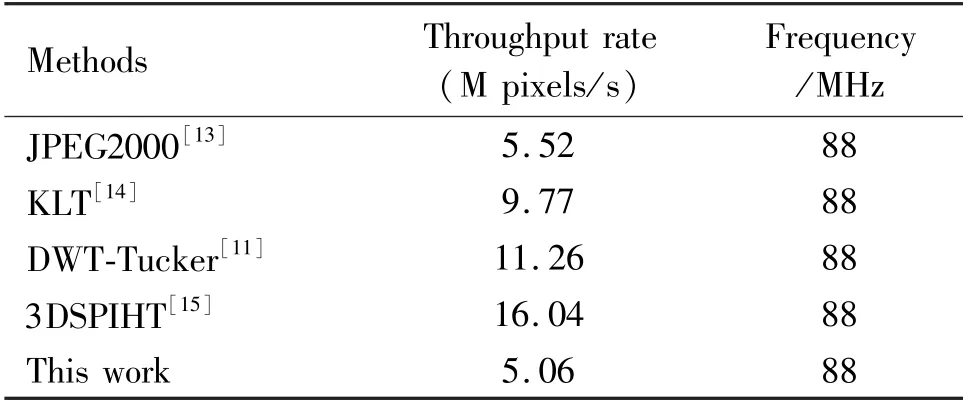
Table 4 Comparison results of data processing speed

The spectral distortion between the original pixel and the reconstructed pixel is often used to measure the fidelity, and the spectral angular distance (SAD) is one of the most commonly used criteria for evaluating multispectral images. Smaller SAD means that compression has lost less information, and the reconstructed multispectral image is more reliable for subsequent applications. For convenience, the mean SAD is used as standard deviation for all pixels to reveal the average spectral distortion of the multispectral image. The results of the mean SAD for different methods are shown in Fig.5. It can be seen from the figure that the method achieves a smaller mean SAD at the maximum bit rates, which indicates that the average spectral distortion of this method is less than other methods. Therefore, the proposed method has good spectral fidelity.

4 Conclusion

This paper proposes a multi-spectral image compression encryption algorithm that combines chaos,wavelet transform and KL transform to solve the security problem of multispectral image compression and transmission. The experimental results show that the method has high signal-to-noise ratio,short operation time, large key space, and it is sensitive to keys and plaintexts with a fine effect in spectrum assurance at the same time.

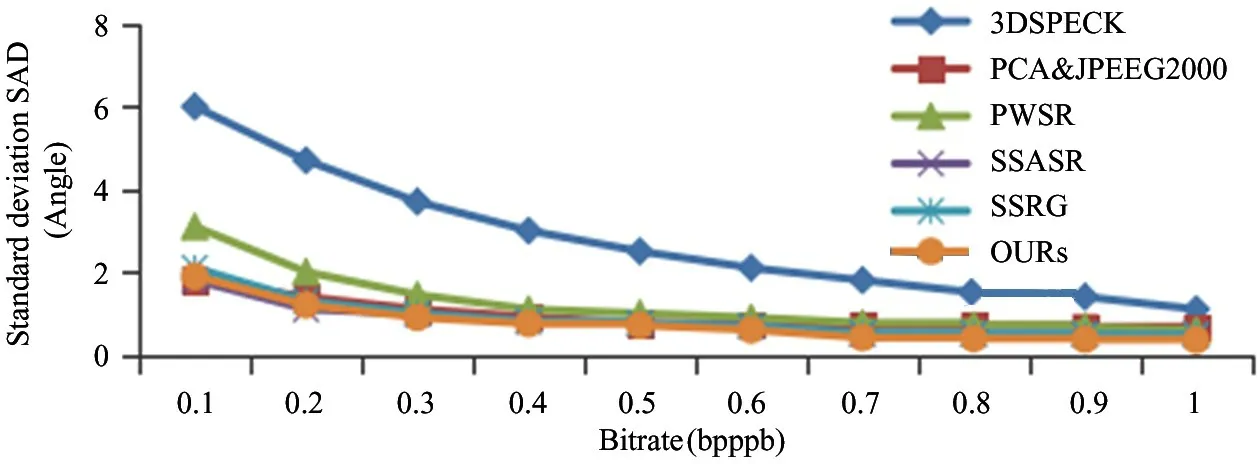
Fig.5 Mean SADs